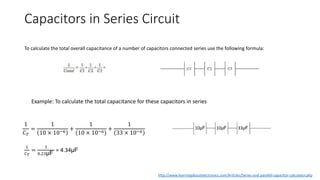
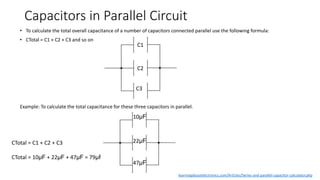
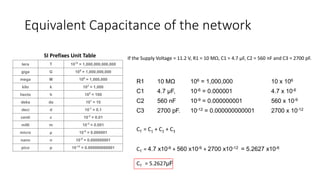
The document discusses capacitors in series, parallel and combination series-parallel circuits. It provides formulas to calculate equivalent capacitance and time constants. For a given circuit with capacitors C1=3.3μF, C2=330nF and C3=3300pF in a combination series-parallel configuration, the equivalent capacitance is 302.725nF. The total charge stored is 50.56μC, with voltages of 1.532V across C1 and 15.168V across C2 and C3. The energy stored is 3.872μJ in C1, 37.961μJ in C2 and 379.614nJ in C3.

1. Electrical and Electronic
Principles
Capacitors

2. Formula
Growth of a capacitor voltage VC = V(1 – e (-t/CR)) = V(1 – e(-t/Շ))
Decay of resistor voltage VR = V.e (-t/CR) = V.e (-t/Շ)
Decay of current flowing I = I.e(-t/CR) = I.e(-t/Շ)
Time constant (secs) Շ(tau) = CR
The energy stored in a capacitor
(joules)
W = ½ CV2
Equations
The following equations may be useful in this assignment:
In a circuit containing one capacitor and one resistor in series connected across a d.c. supply at ALL times while the current is flowing we can say,
V = VC + VR and V = q/(C + iR) (q = charge on the capacitor)
In a circuit containing one capacitor and one resistor in series
connected across a d.c. supply at ALL times while the current is
flowing we can say,
V = VC + VR and V = q/(C + iR) (q = charge on the capacitor)

3. Capacitors in Series Circuit
To calculate the total overall capacitance of a number of capacitors connected series use the following formula:
Example: To calculate the total capacitance for these capacitors in series
10μF 10μF 33μF
1
𝐶 𝑇
=
1
10 × 10−6
+
1
10 × 10−6
+
1
33 × 10−6
1
𝐶 𝑇
=
1
0.23μF
= 4.34μF
http://www.learningaboutelectronics.com/Articles/Series-and-parallel-capacitor-calculator.php

4. Capacitors in Parallel Circuit
• To calculate the total overall capacitance of a number of capacitors connected parallel use the following formula:
• CTotal = C1 + C2 + C3 and so on
CTotal = C1 + C2 + C3
CTotal = 10μF + 22μF + 47μF = 79μF
C1
C2
C3
Example: To calculate the total capacitance for these three capacitors in parallel.
http://www.learningaboutelectronics.com/Articles/Series-and-parallel-capacitor-calculator.php
22μF
10μF
47μF

5. Capacitors in Parallel Circuit
• Capacitors in Parallel Circuit
• What is the Equivalent Capacitance of the network?
• If the Supply Voltage = 11.2 V, R1 = 10 MΩ, C1 = 4.7 μF, C2 = 560 nF and C3 = 2700 pF.

6. Equivalent Capacitance of the network
tera T 1012
= 1,000,000,000,000
giga G 109
= 1,000,000,000
mega M 106
= 1,000,000
kilo k 103
= 1,000
hecto h 102
= 100
deka da 101
= 10
deci d 10-1
= 0.1
centi c 10-2
= 0.01
milli m 10-3
= 0.001
micro µ 10-6
= 0.000001
nano n 10-9
= 0.000000001
pico p 10-12
= 0.000000000001
SI Prefixes Unit Table
R1 10 MΩ 106 = 1,000,000 10 x 106
C1 4.7 μF, 10-6 = 0.000001 4.7 x 10-6
C2 560 nF 10-9 = 0.000000001 560 x 10-9
C3 2700 pF. 10-12 = 0.000000000001 2700 x 10-12
If the Supply Voltage = 11.2 V, R1 = 10 MΩ, C1 = 4.7 μF, C2 = 560 nF and C3 = 2700 pF.
CT = C1 + C2 + C3
CT = 4.7 x10-6 + 560 x10-9 + 2700 x10-12 = 5.2627 x10-6
CT = 5.2627μF

7. What is the Equivalent Capacitance of the network?
If the Supply Voltage (V) = 16.7 V, R1 = 10 MΩ, C1 = 3.3 μF, C2 = 330 nF and C3 = 3300 pF.
•
1
𝐶 𝑇
=
1
𝐶1
+
1
𝐶2
+
1
𝐶3
•
1
𝐶 𝑇
=
1
3.3×10−6 +
1
0.33×10−6 +
1
0.0033×10−6
•
1
𝐶 𝑇
= 306363636.4
• 𝐶 𝑇 = 3.264094955 × 10−9
• 𝐶 𝑇 = 3.264 𝑛𝐹

8. How Long Does It Take to Charge a Capacitor?
• A capacitor charges to 63% of the supply voltage that is charging it after one time period. After 5 time periods, a
capacitor charges up to over 99% of its supply voltage. Therefore, it is safe to say that the time it takes for a
capacitor to charge up to the supply voltage is 5 time constants.
• To calculate the time constant of a capacitor, the formula is τ=RC. This value yields the time (in seconds) that it
takes a capacitor to charge to 63% of the voltage that is charging it up. After 5 time constants, the capacitor will
charged to over 99% of the voltage that is supplying.
• Therefore, the formula to calculate how long it takes a capacitor to charge to is:
Time for a Capacitor to Charge= 5RC
• After 5 time constants, for all extensive purposes, the capacitor will be charged up to very close to the supply
voltage. A capacitor never charges fully to the maximum voltage of its supply voltage, but it gets very close.
• Supply voltage 9V Resistor 3KΩ Capacitor 1000µF
• One time constant, τ=RC=(3KΩ)(1000µF)=3 seconds. 5x3=15 seconds. So it takes the capacitor about 15 seconds to
charge up to near 9 volts.

9. What is the Voltage across the Network after 0.01 seconds
Vc is the voltage across the capacitor
• Vs is the supply voltage 16.7V
• t is the elapsed time since the application of the supply voltage
• RC is the time constant of the RC charging circuit
• The time constant, τ is found using the formula T = C x R in seconds.
• 𝐶 𝑇 = 3.264 𝑛𝐹
• R1 = 10 MΩ
• 𝑉𝐶 = 𝑉𝑆 1 − 𝑒
−
𝑡
𝐶𝑅
• 𝑉𝐶 = 16.7 1 − 𝑒
−
0.01
0.003264094×10−6 × 10×106
• Break the calculation down into smaller parts to prevent an error on your calculator.
• 𝑉𝐶 = 16.7 1 − 𝑒−0.3063636364
• 𝑉𝐶 = 4.406814518
• 𝑉𝐶 = 4.407 𝑉
What is the Voltage accross the Network after 50 seconds?
Answer:

10. What is the Charge stored in the capacitors when it is fully charged?
C= 3.264094955 × 10−9
V = 16.7 V
𝑄 = 𝐶𝑉
𝑄 = 3.264094955 × 10−9
× 16.7
𝑄 = 54.51038575 × 10−9
𝑄 = 54.51 𝑛𝐶
Charge and Energy Stored
The amount of charge (symbol Q) stored by a capacitor is given by:
Charge, Q = C × V where:
Q = charge in coulombs (C)
C = capacitance in farads (F)
V = voltage in volts (V)

11. What is the Energy stored in the capacitors when they are fully charged?
C= 3.264094955 × 10−9
V = 16.7 V
𝑊 =
1
2
𝐶𝑉2
𝑊 =
1
2
3.264094955 × 10−9
× 16.72
𝑊 = 455.161721 × 10−9
𝑊 = 455.162𝑛𝐽
When they store charge, capacitors are also storing energy:
Energy, E = ½QV = ½CV² where, E = energy in joules (J).
Note that capacitors return their stored energy to the circuit. They do not 'use up'
electrical energy by converting it to heat as a resistor does. The energy stored by a
capacitor is much smaller than the energy stored by a battery so they cannot be used
as a practical source of energy for most purposes.

12. Capacitors in combination Series/Parallel Circuit
If the Supply Voltage (V) = 16.7 V, R1 = 10 MΩ, C1 = 3.3 μF, C2 = 330 nF
and C3 = 3300 pF.
What is the Equivalent Capacitance of the network?
1
𝐶 𝑇
=
1
𝐶1
+
1
𝐶 𝑃
𝐶 𝑃 = 𝐶2 + 𝐶3
𝐶 𝑃 = (0.33 × 10−6) + (0.0033 × 10−6)
𝐶 𝑃 = 0.3333 × 10−6
1
𝐶 𝑇
=
1
3.3 × 10−6
+
1
0.3333 × 10−6
1
𝐶 𝑇
= 3.303330333 × 106
𝐶 𝑇 = 302.7247956 × 10−9
𝐶 𝑇 = 302.725 𝑛𝐹

13. What is the Total Charge stored in the network?
• 𝐶 𝑇 = 302.725 𝑛𝐹
• V=16.7V
• 𝑄 = 𝐶𝑉
• 𝑄 = 302.7247956 × 10−9
× 16.7
• 𝑄 = 5.055504087 × 10−6
• 𝑄 = 50.56 𝑢𝐶

14. What is the Potential Difference (Voltage) across C1
• 𝑉 =
𝑄
𝐶
• 𝑉1 =
5.055504087×10−6
3.3×10−6
• 𝑉1 = 1.531970935
• 𝑉1 = 1.532 𝑉

15. What is the Potential Difference ( Voltage) across C2/3?
• 𝑉23 =
𝑄
𝐶
• 𝑉23 =
5.055504087×10−6
(0.33×10−6)+(0.0033×10−6)
• 𝑉23 =
5.055504087×10−6
(0.33×10−6)+(0.0033×10−6)
• 𝑉23 = 15.16802906
• 𝑉23 = 15.168 𝑉

16. What is the Energy stored in C1?
• 𝑊 =
1
2
𝐶𝑉1
2
• 𝑊1 =
1
2
× 3.3 × 10−6 × 1.5319709352
• 𝑊1 = 3.87244266 × 10−6
• 𝑊1 = 3.872 𝑢𝐽
If the Supply Voltage (V) = 16.7 V, R1 = 10 MΩ, C1 = 3.3 μF, C2 = 330 nF and C3 = 3300 pF.
𝑉1 = 1.532 𝑉

17. What is the Energy stored in C2?
• 𝑊 =
1
2
𝐶𝑉23
2
• 𝑊1 =
1
2
× 330 × 10−9 × 15.168029062
• 𝑊1 = 37.96140242 × 10−6
• 𝑊1 = 37.961 𝑢𝐽
If the Supply Voltage (V) = 16.7 V, R1 = 10 MΩ, C1 = 3.3 μF, C2 = 330 nF and C3 = 3300 pF.
𝑉23 = 15.168 𝑉

18. What is the Energy stored in C3?
• 𝑊 =
1
2
𝐶𝑉23
2
• 𝑊1 =
1
2
× 3300 × 10−12 × 15.168029062
• 𝑊1 = 379.6140242 × 10−9
• 𝑊1 = 379.614 𝑛𝐽
If the Supply Voltage (V) = 16.7 V, R1 = 10 MΩ, C1 = 3.3 μF, C2 = 330 nF and C3 = 3300 pF.
𝑉23 = 15.168 𝑉