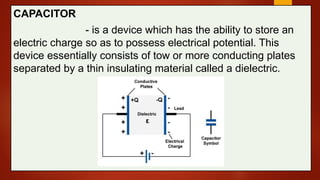
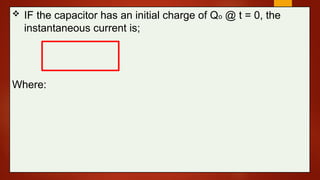
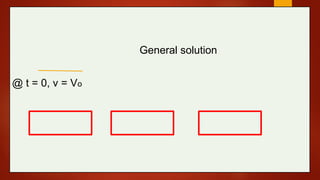
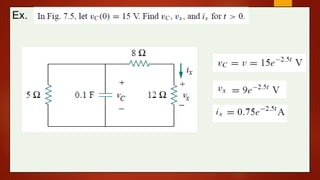
The document explains the function and characteristics of capacitors in RC circuits, including concepts such as capacitance, time constants, and formulas for instantaneous current and voltage in both charging and discharging scenarios. It provides examples and calculations for various capacitor and resistor configurations, illustrating the behavior of the circuit over time. Key topics include energy storage, power dissipation, and transient responses in DC circuits.

1. DC Source
RC Circuits

2. CAPACITOR
- is a device which has the ability to store an
electric charge so as to possess electrical potential. This
device essentially consists of tow or more conducting plates
separated by a thin insulating material called a dielectric.

4. Capacitance – is a measure on the ability of a device (called
capacitor) to store an electric charge.
Farad – the standard unit for capacitance. The capacitance of
the capacitor is one farad if a voltage of one volt
stores a charge of one coulomb in it.
- the unit “Farad” was named after the British
physicist Michael Faraday. Faraday was the one who
discovered electromagnetic induction.
𝐶=
𝑄
𝐸
Where:
C = capacitance
(farad)
Q = charge
(coulomb)
E = voltage

5. DC Source
RC Circuits

7. The Time Constant of an RC Circuit
The time constant (tau or of an RC circuit is the time
required for the current to decay or fall down to 63.2 % of its
initial value to its steady – state value. This is also the time
required for the voltage across the capacitor to rise to 63.2 %
of its final value at steady – state.
𝜏=𝑅𝐶

9. *
Where:
C = capacitance
(farad)
Q = charge
(coulomb)
E = voltage
across
capacitor (volts)
i = current
(amperes)

10. RC – DC Circuit
KVL:
𝑬
𝑹
𝒕 =𝟎
𝒕 =𝟎
𝒊
+ 𝑬 𝑹 −
𝑪

12. General solution
 IF the capacitor has no initial charge @ t = 0. The
instantaneous current in the RC Circuit is:
t = 0 q = 0 i = E/R

13.  IF the capacitor has an initial charge of Qo @ t = 0, the
instantaneous current is;
Where:

14. INSTANTANEOUS VOLTAGE DROP ACROSS THE
RESISTOR (Qo = 0)

15. INSTANTANEOUS VOLTAGE DROP ACROSS THE
CAPACITOR (Qo = 0)

16. @ t = 0 ; Ec = 0

17. INSTANTANEOUS POWER DISSIPATED

18. INSTANTANEOUS POWER DISSIPATED

19. INSTANTANEOUS POWER DISSIPATED

20. INSTANTANEOUS CHARGE STORED BY CAPACITOR
KVL:
*
*
linear D.E.

21. General solution

22. @ t = 0; q = 0
@ t = 0; q = Qo

23. TRANSIENT DECAY
 Source Free
KVL:

24. General solution
@ t = 0, v = Vo

25. ENERGY STORED

26. If the capacitor has no initial charge at t = 0, the
instantaneous current in the RC circuit is found by the formula,
If the capacitor has an initial charge Qo at t = 0, the
instantaneous current in the RC circuit is found by the formula,
𝒊=
𝑬
𝑹
𝒆
−
𝒕
𝑹𝑪
𝒊=
( 𝑬 ± 𝑬𝑪 )
𝑹
𝒆
−
𝒕
𝑹𝑪
Where:
= voltage across the capacitor if discharging
= voltage across the capacitor if charging
E = DC supply voltage
Qo = initial charge of the capacitor

27. SUMMARY: RC TRANSIENT CIRCUIT (DC CIRCUIT)
Instantaneous Voltage Drop
across Resistor (Qo = 0)
Instantaneous Voltage Drop
across Capacitor (Qo = 0)
𝑬 𝑹=𝑬𝒆
−𝒕
𝑹𝑪
𝑬𝑪 =𝑬(𝟏− 𝒆
−𝒕
𝑹𝑪
)

28. SUMMARY: RC TRANSIENT CIRCUIT (DC CIRCUIT)
Instantaneous Power Dissipated
across Resistor
Instantaneous Power
Dissipated across Capacitor
Total Instantaneous Power
Dissipated
𝑷𝑹=
𝑬
𝟐
𝑹
𝒆
−𝟐 𝒕
𝑹𝑪
𝑷 𝑪 =
𝑬
𝟐
𝑹
(𝒆
− 𝒕
𝑹𝑪
−𝒆
−𝟐 𝒕
𝑹𝑪
)
𝑷 𝑻 =
𝑬
𝟐
𝑹
𝒆
−𝒕
𝑹𝑪

29. SUMMARY: RC TRANSIENT CIRCUIT (DC CIRCUIT)
Instantaneous Charge Stored By
Capacitor (Qo = 0)
Instantaneous Charge Stored
By Capacitor (q = Qo)
𝒒=𝑪𝑬 (𝟏− 𝒆
−𝒕
𝑹𝑪
)
𝒒=𝑪𝑬 +(𝑸𝒐 − 𝑪𝑬 )𝒆
−𝒕
𝑹𝑪

30. SUMMARY: RL TRANSIENT CIRCUIT (DC CIRCUIT)
Time Constant
Transient Decay (Source Free)
𝒗=𝑽 𝒐 𝒆
− 𝒕
𝑹𝑪
𝜏=
1
𝑅𝐶
𝒊=𝑰𝒐 𝒆
−𝒕
𝑹𝑪
𝒒=𝑸𝒐 𝒆
−𝒕
𝑹𝑪

31. Ex. A 80 μF capacitor in series with a voltmeter of 10 kΩ
resistance is connected suddenly across a 100 V source. What
is the voltmeter reading after 0.4 sec?
Ans. 60.6 V
Solution:
Given: C = 80 μFR = 10 kΩE = 100 V
Voltmeter = ? @ t = 0.4 s

32. Ex. A 600 μF is charged to 400 V. It is then discharged through
a 2 kΩ resistor. Calculate the voltage across the capacitor
after 3 sec.
Ans. 32.834 V
Solution:
Given: C = 600 μF E = 400 V R = 2 kΩ
Ec = ? @ t = 3 sec

33. Ex. A 20 Ω resistance and 0.001 farad capacitance C are in
series. A direct current voltage E of 100 volts is applied across
the series circuit. Find the resulting current at t = 0.01 sec?
Ans. 3.03 A
Solution:
Given: R = 20 Ω C = 0.001 F E = 100 V
i = ? @ t = 0.01 sec

34. Ex. A 50 μF capacitor is connected across a 400 V DC source.
It is then discharged through a voltmeter whose resistance is
100 kΩ. How long will it take for the capacitor to discharge to
1.8 J of stored energy?
Solution:
Given: C = 50 μF E = 400 VR = 100 kΩ t = ?
@ w = 1.8 J

35. Ex.
Ans.

36. Solution:
@ t < 0 (before the switch is open)

37. Solution:
@ t > 0 (after the switch is open)

38. Solution:

39. Ex.
Ans.