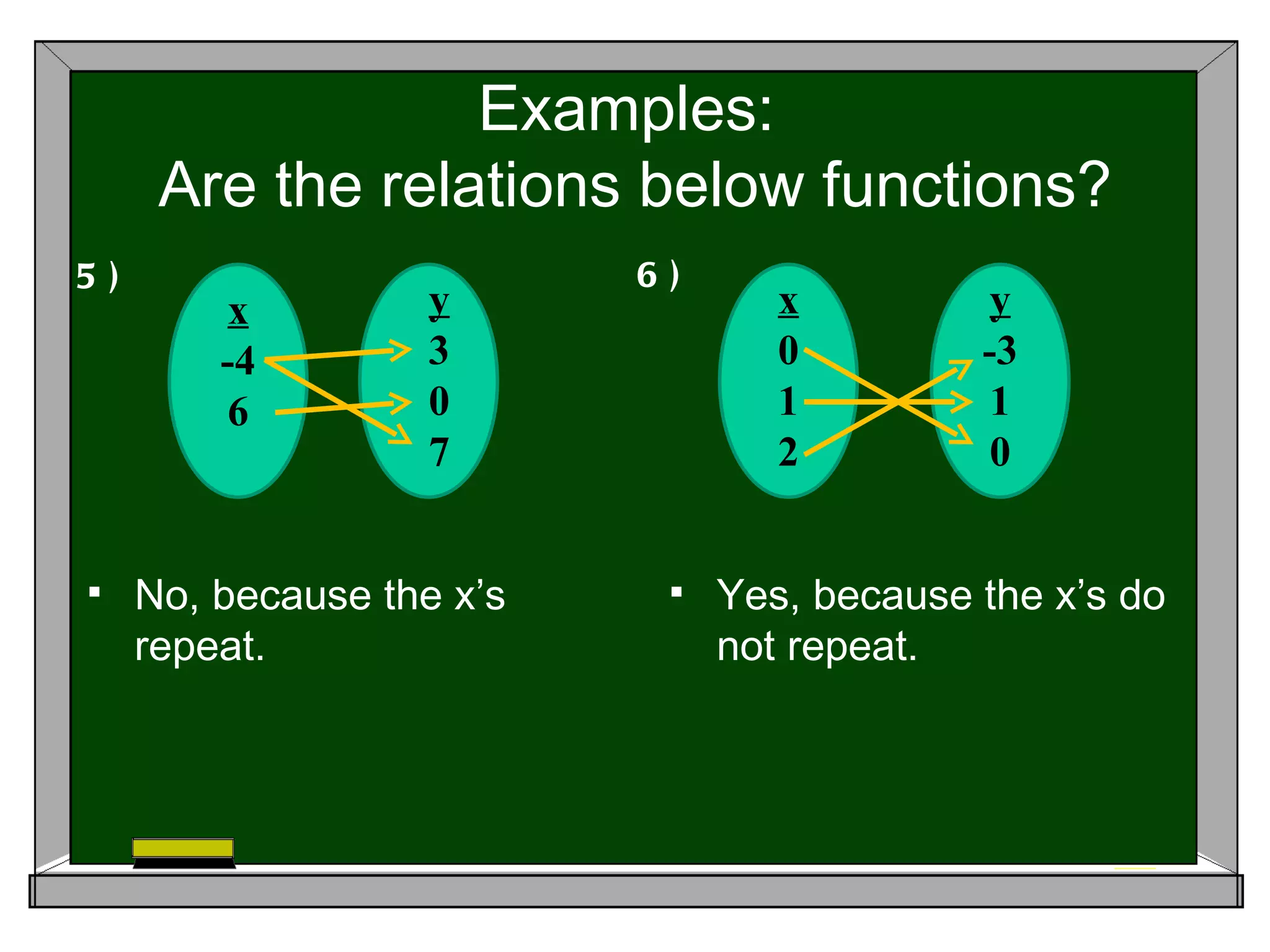
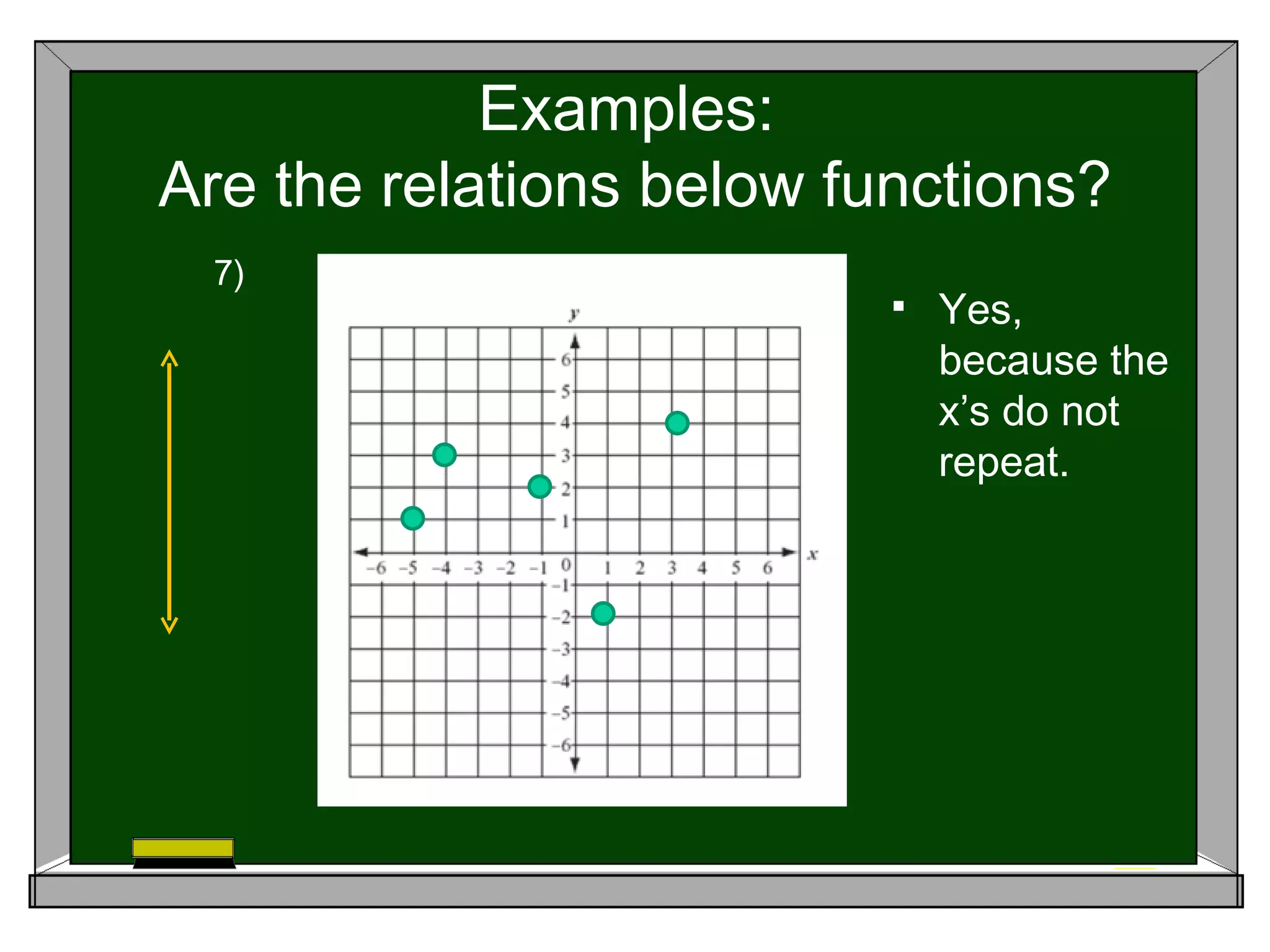
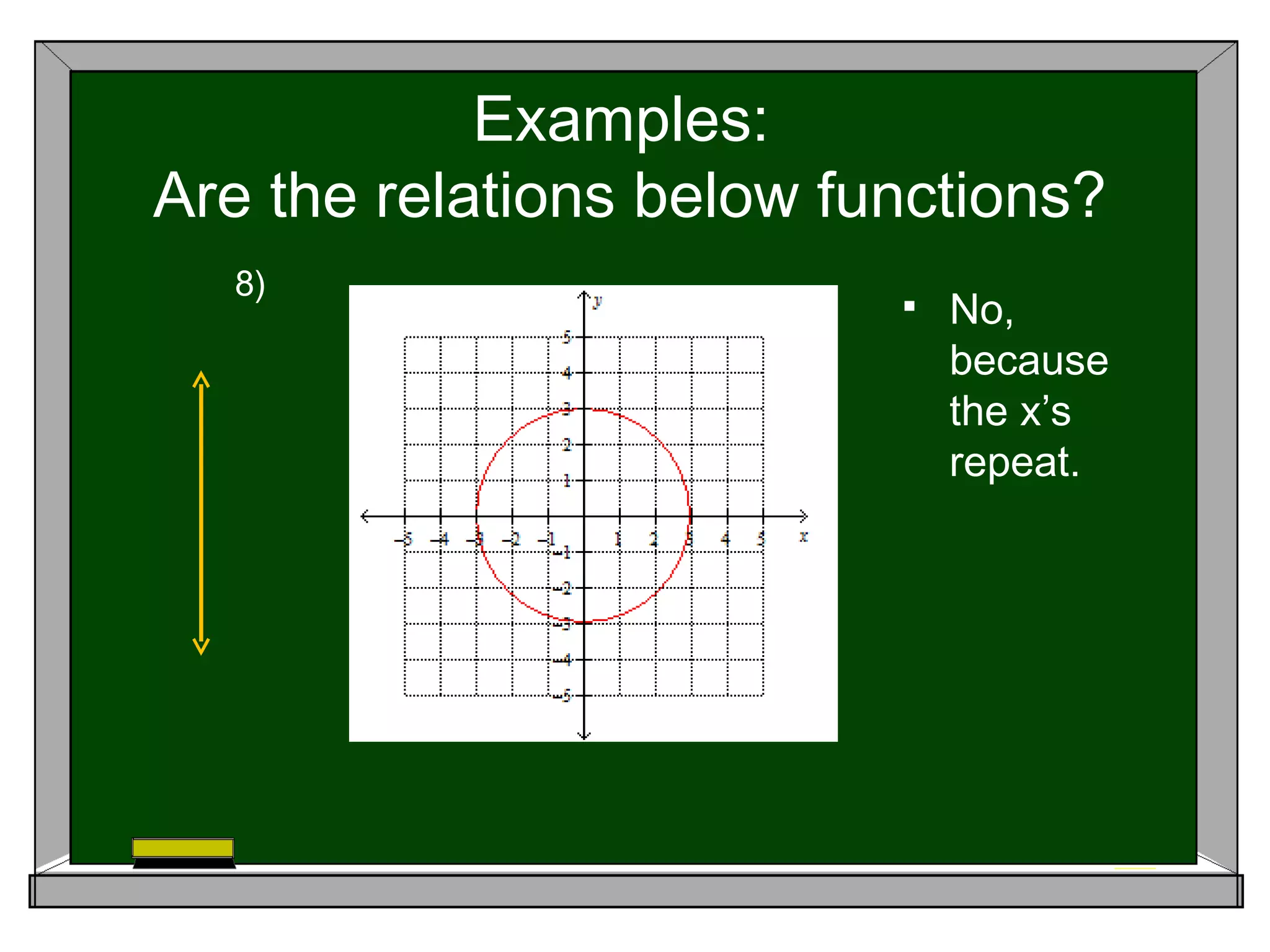
A function is a special type of relation where each input is mapped to exactly one output. For a relation to be a function, the inputs or x-values cannot repeat. The document provides examples of relations and identifies which ones are functions based on this criterion. It also explains that the vertical line test can be used to determine if a graphed relation is a function - if a vertical line intersects the graph more than once, it is not a function.

1. What is a function?
Unit 4 Lesson 3
Remediation Activity 1

2. From Lessons 1 and 2:
 Ordered pairs are always written as (x, y)
 A relation is a set of ordered pairs
 Domain: the set of all "x" values in a relation
 Range: the set of all "y" values in a relation
 Relations can be expressed as:
1) ordered pairs
2) a table
3) a graph
4) a mapping

3. We are going to review:
 what a function is
 how to determine if relations are
functions

4. What is a function?
 A function is a special type of relation
that relates each x value to only one
y value.
 In other words, the x’s do not repeat.

5. Examples:
Are the relations below functions?
1) { ( - 1, 2 ) , ( 3 , 2 ) , ( 4 , 2 ) { ( - 3 , 2 ) , ( -1, 4 ) , ( 0 , 0 ) ,
-6 ) } ( 0 , 1) }
 Yes, because the x’s do  No, because the x’s
not repeat. repeat.

6. Examples:
Are the relations below functions?
3) X Y 4) X Y
-2 0 -2 0
5 -1 0 -1
5 7 2 9
 No, because the x’s  Yes, because the x’s do
repeat. not repeat.

7. Examples:
Are the relations below functions?
5) 6)
x y x y
-4 3 0 -3
6 0 1 1
7 2 0
 No, because the x’s  Yes, because the x’s do
repeat. not repeat.

8. Examples:
Are the relations below functions?
7)
 Yes,
because the
x’s do not
repeat.

9. Examples:
Are the relations below functions?
8)
 No,
because
the x’s
repeat.

10. What did we learn?
 A function is a special type of relation that relates each
x value with only one y value.
 In other words, the x's DO NOT repeat!

11. What did we learn?
 We can use the Vertical Line Test to determine if a
graph is a function.
 If a vertical line intersects the relation's graph more than
one time, then the relation is NOT a function.
 If a vertical line intersects the relation's graph only one
time, then the relation IS a function.