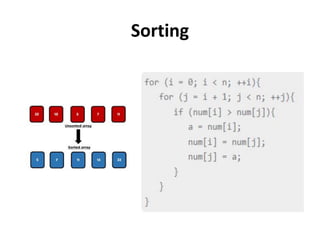
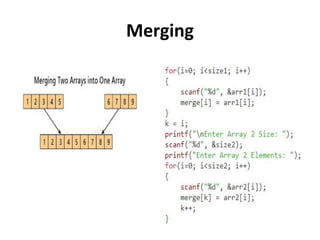
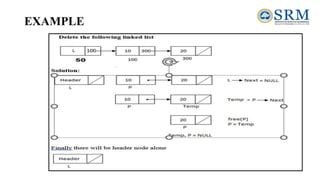
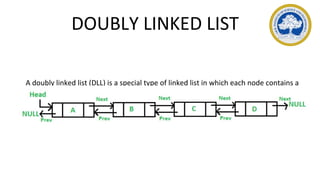
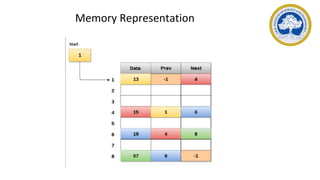
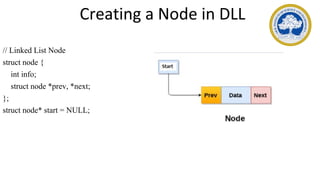
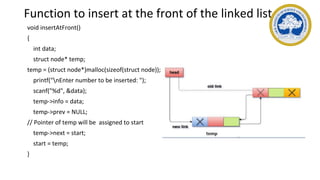
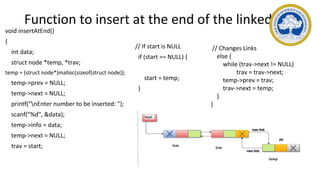
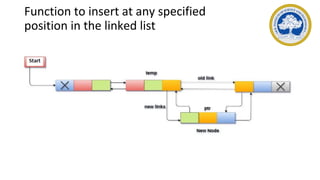
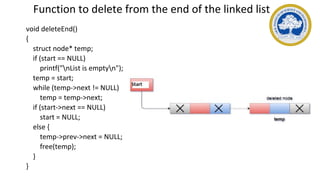
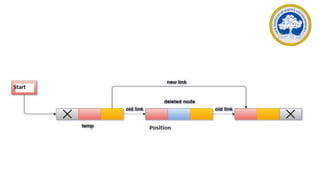
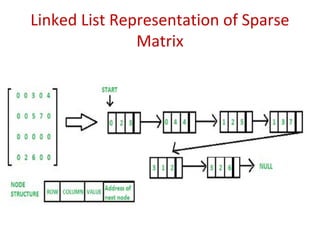
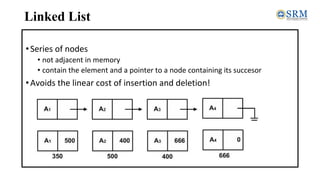
This document discusses representations of sparse matrices using linked lists. It explains that sparse matrices, which contain mostly zero values, can be stored more efficiently using a triplet representation or linked representation rather than a standard 2D array. The triplet representation stores only the non-zero elements, their row and column indices, and matrix size information. It provides an example of a 4x5 sparse matrix represented as a triplet array with 6 non-zero elements. Linked representation stores the sparse matrix as a linked list, where each node contains the row, column and value of a non-zero element. Applications of sparse matrix representations include storing large sparse datasets efficiently.








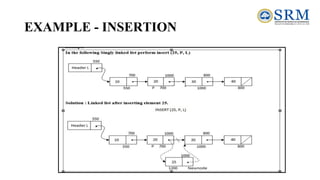




















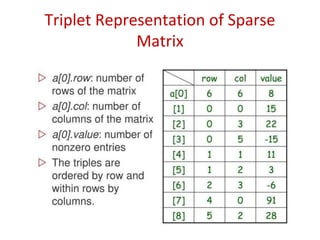
![Triplet Representation of Sparse Matrix (Using Array)
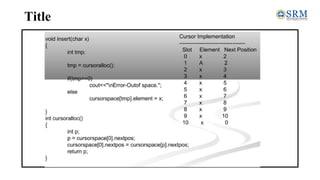
int main()
{
// Assume 4x5 sparse matrix
int sparseMatrix[4][5] =
{
{0 , 0 , 3 , 0 , 4 },
{0 , 0 , 5 , 7 , 0 },
{0 , 0 , 0 , 0 , 0 },
{0 , 2 , 6 , 0 , 0 }
};
int size = 0;
for (int i = 0; i < 4; i++)
for (int j = 0; j < 5; j++)
if (sparseMatrix[i][j] != 0)
size++;
// number of columns in compactMatrix (size) must
be
// equal to number of non - zero elements in
// sparseMatrix
int compactMatrix[3][size];
// Making of new matrix
int k = 0;
for (int i = 0; i < 4; i++)
for (int j = 0; j < 5; j++)
if (sparseMatrix[i][j] != 0)
{
compactMatrix[0][k] = i;
compactMatrix[1][k] = j;
compactMatrix[2][k] = sparseMatrix[i][j];
k++;
}
for (int i=0; i<3; i++)
{
for (int j=0; j<size; j++)
printf("%d ", compactMatrix[i][j]);
printf("n");
}
return 0;
}](https://image.slidesharecdn.com/unit-2-231018060356-c2718ff8/85/Unit-2-pdf-42-320.jpg)

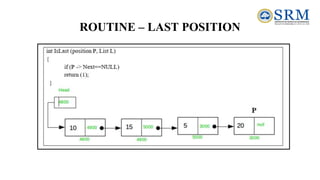
![Sparse Matrix Operations
• Transpose of a sparse matrix.
• What is the transpose of a matrix?
row col value row col value
a[0] 6 6 8 b[0] 6 6 8
[1] 0 0 15 [1] 0 0 15
[2] 0 3 22 [2] 0 4 91
[3] 0 5 -15 [3] 1 1 11
[4] 1 1 11 [4] 2 1 3
[5] 1 2 3 [5] 2 5 28
[6] 2 3 -6 [6] 3 0 22
[7] 4 0 91 [7] 3 2 -6
[8] 5 2 28 [8] 5 0 -15
transpose](https://image.slidesharecdn.com/unit-2-231018060356-c2718ff8/85/Unit-2-pdf-45-320.jpg)


























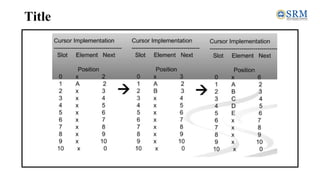
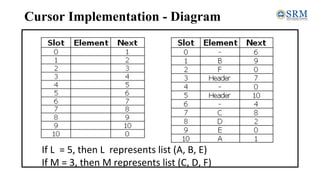
![List - Implementation
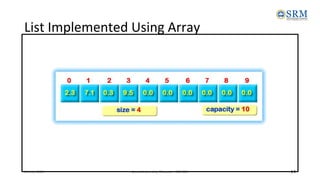
•Lists can be implemented using:
• Arrays
• Linked List
• Cursor [Linked List using Arrays]](https://image.slidesharecdn.com/unit-2-231018060356-c2718ff8/85/Unit-2-pdf-78-320.jpg)














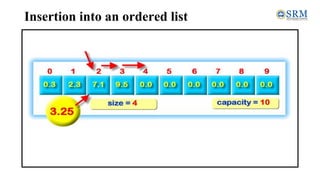








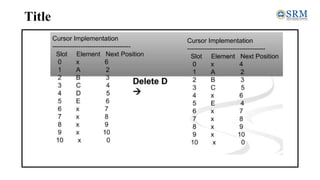
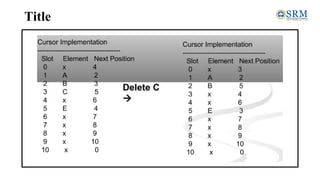




![Deletion
• Input the size of the array arr[] using num, and then declare
the pos variable to define the position, and i represent the
counter value.
• Input the position of the particular element to delete from an
array.
• Remove the particular element and shift the rest elements
position to the left side in an array.
• Display the resultant array after deletion or removal of the
element from an array.](https://image.slidesharecdn.com/unit-2-231018060356-c2718ff8/85/Unit-2-pdf-113-320.jpg)