This document discusses using support vector machines (SVM) for unattended parameter fitting to monitor nonlinear profiles. It presents an illustrative example of using SVM regression to smooth measured density profiles of engineered wood boards. The key points are: 1) SVM regression requires selecting parameters C (regularization parameter) and ε (width of insensitive zone), which control the complexity and deviations of the model. 2) Methods are presented for unattended selection of C and ε based on properties of the input noise and data. 3) The SVM model is applied to smooth individual nonlinear profiles from measured wood board density data and identify potential outliers.

1. Unattended SVM
parameters fitting for
monitoring nonlinear
profiles
Emilio L. Cano (University of Castilla-La Mancha)
Javier M. Moguerza (Rey Juan Carlos University)
Mariano Prieto (ENUSA Industrias Avanzadas)

2. Statistical Process Control
Assignable causes of variation may be
found and eliminated
Walter A. Shewhart
2

3. Statistical Process Control (cont.)
Observation
6
7
8
12
13
14
10.08
1 2 3 4 5 6 7 8 9 1011121314151617181920
q q
q
q
q
q
q
q q
q
q
q
q q
q
q
q
q
q
q
3

4. Statistical Process Control (cont.)
Observation
6
7
8
12
13
14
10.28
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
q q
q
q
q
q
q
q q
q
q
q
q q
q
q
q
q
q
q
q Special cause
4

5. Nonlinear profiles
0.0 0.1 0.2 0.3 0.4 0.5
45
50
55
60
X−Location
Measurement
5

6. Nonlinear profiles
0.0 0.1 0.2 0.3 0.4 0.5
45
50
55
60
X−Location
Measurement
One function per sample (instead of a data point)
5

7. Illustrative example
Engineered woodboards
Data set of 50 boards
Sample of 5 boards per shift
Quality characteristic: density
Total measurements: 500
Every 0.001 in along the board
6

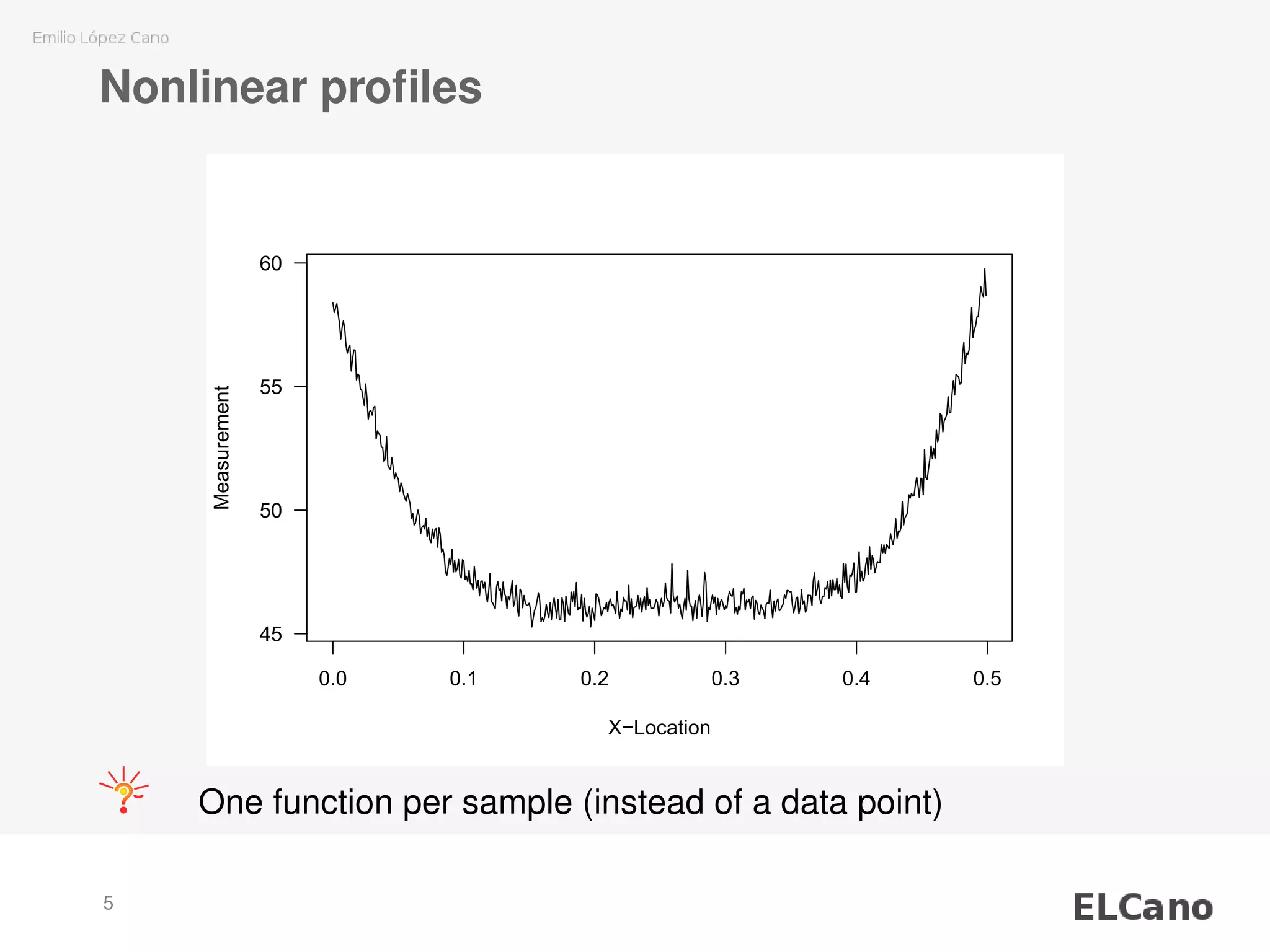
8. Illustrative example (cont.)
Data
library(SixSigma)
str(ss.data.wbx)
## num [1:500] 0 0.001 0.002 0.003 0.004 0.005 0.006 0.007
str(ss.data.wby)
## num [1:500, 1:50] 58.4 58 58.2 58.4 57.9 ...
## - attr(*, "dimnames")=List of 2
## ..$ : NULL
## ..$ : chr [1:50] "P1" "P2" "P3" "P4" ...
7

9. Illustrative example (cont.)
plotProfiles(profiles = ss.data.wby,
x = ss.data.wbx)
0.0 0.1 0.2 0.3 0.4 0.5
35
40
45
50
55
60
65
Profiles
8

10. Support Vector Machines (SVM)
SVM regression model
Given response y, input space x:
y = r(x) + δ
r(x) feature space (higher dimension than x)
r(x): non-linear, high dimensional transformation of x input vector
Then, a linear combination over the feature space is the prediction
model:
f(x, ω) =
j
ωj, gj(x)
9

11. Support Vector Machines (SVM) (cont.)
SVM regression parameters
Regression estimates are obtained minimizing the ε-intensive loss
function. This function contains two input parameters: ε and C
(regularization parameter)
Details: Vapnik, V. (1998). Statistical learning theory. New York: Wiley;
Vapnik, V. (1999). The nature of statistical learning theory (2nd ed).
Berlin: Springer.
10

12. Support Vector Machines (SVM) (cont.)
Parameters selection
C trade off between model complexity and deviations larger than
ε in optimization
ε controls the width of the ε-insensitive zone
Several practical approaches (cross validation, experts opinion,
. . . )
11

13. (unattended) Parameters selection
Regularization parameter C
C = max{|y + 3σy|, |y − 3σy|}
max(c(abs(mean(y) + 3*sd(y)), abs(mean(y) - 3*sd(y))))
ε parameter
ε = 3σ
log n
n
3*par.sigma*sqrt(log(nrowprofiles)/nrowprofiles)
12

14. (unattended) Parameters selection (cont.)
Input noise level σ
An approximation using polynomials
mloess <- loess(y ~ x)
yhat <- predict(mloess, newdata = x)
deltas <- y - yhat
par.sigma <- sd(deltas)
Details: Cherkassky, V and Ma, Y (2004). Practical selection of SVM
parameters and noise estimation for SVM regression. Neural
Networks, 17(1), 113-126
13

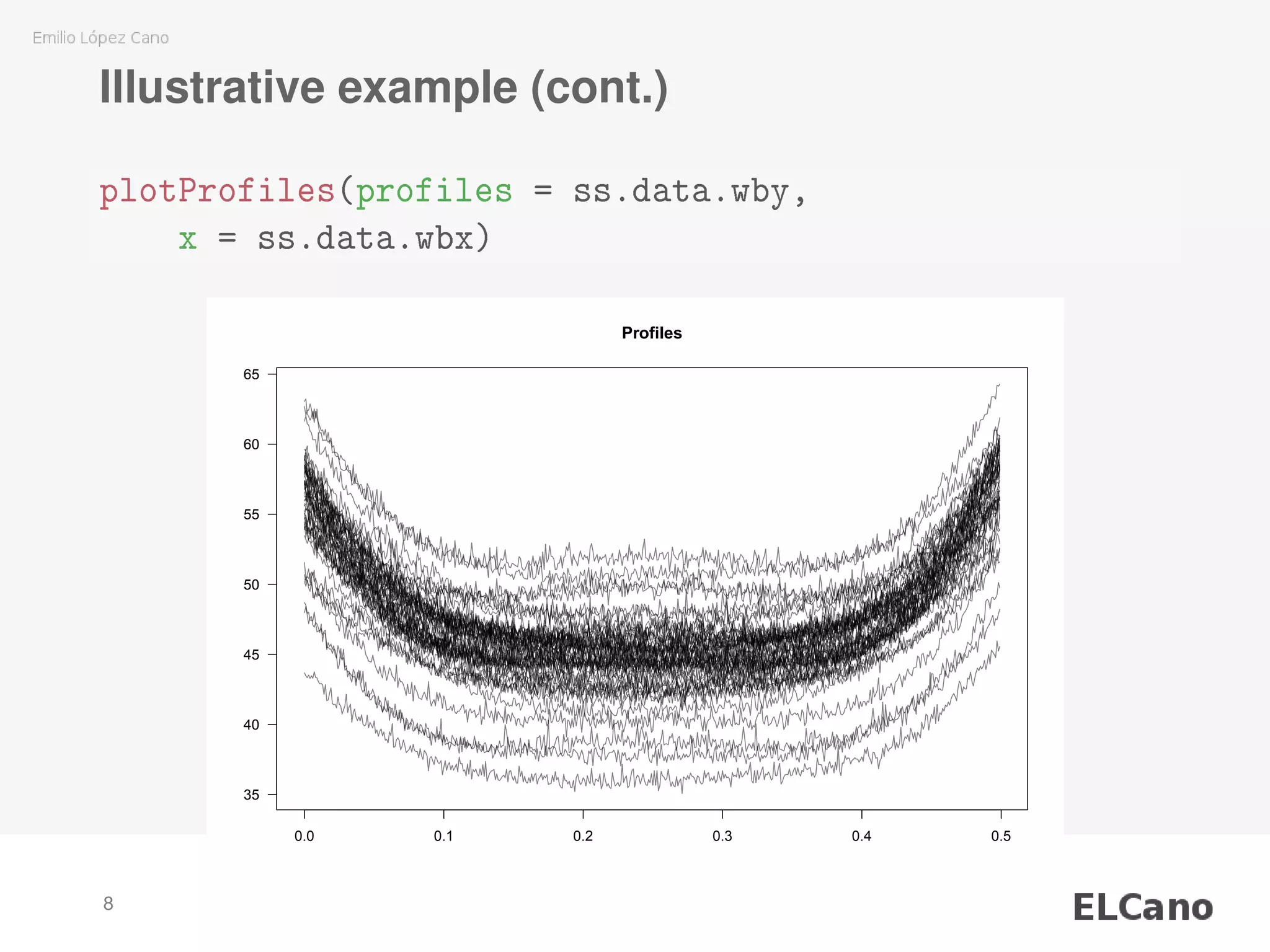
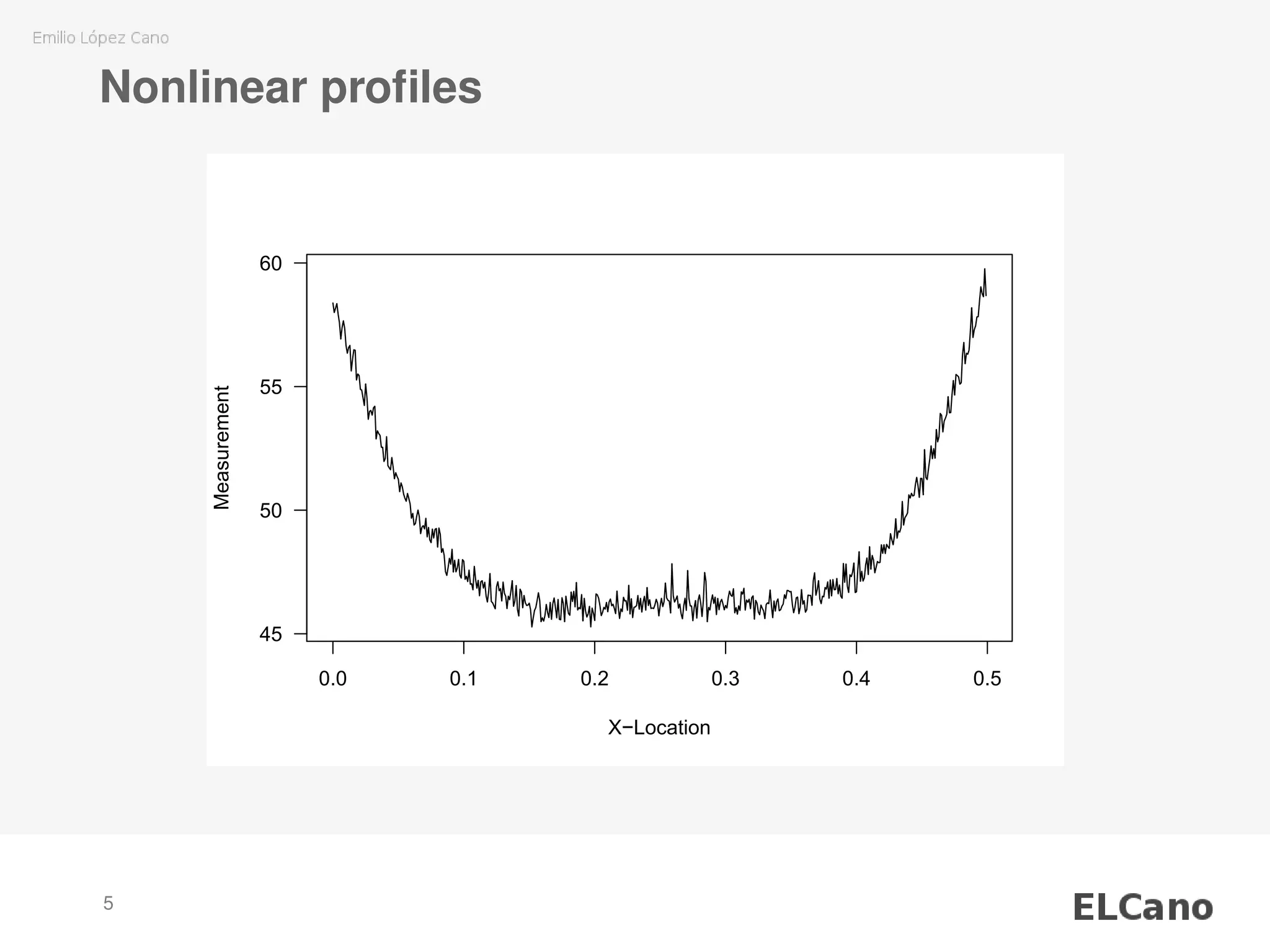
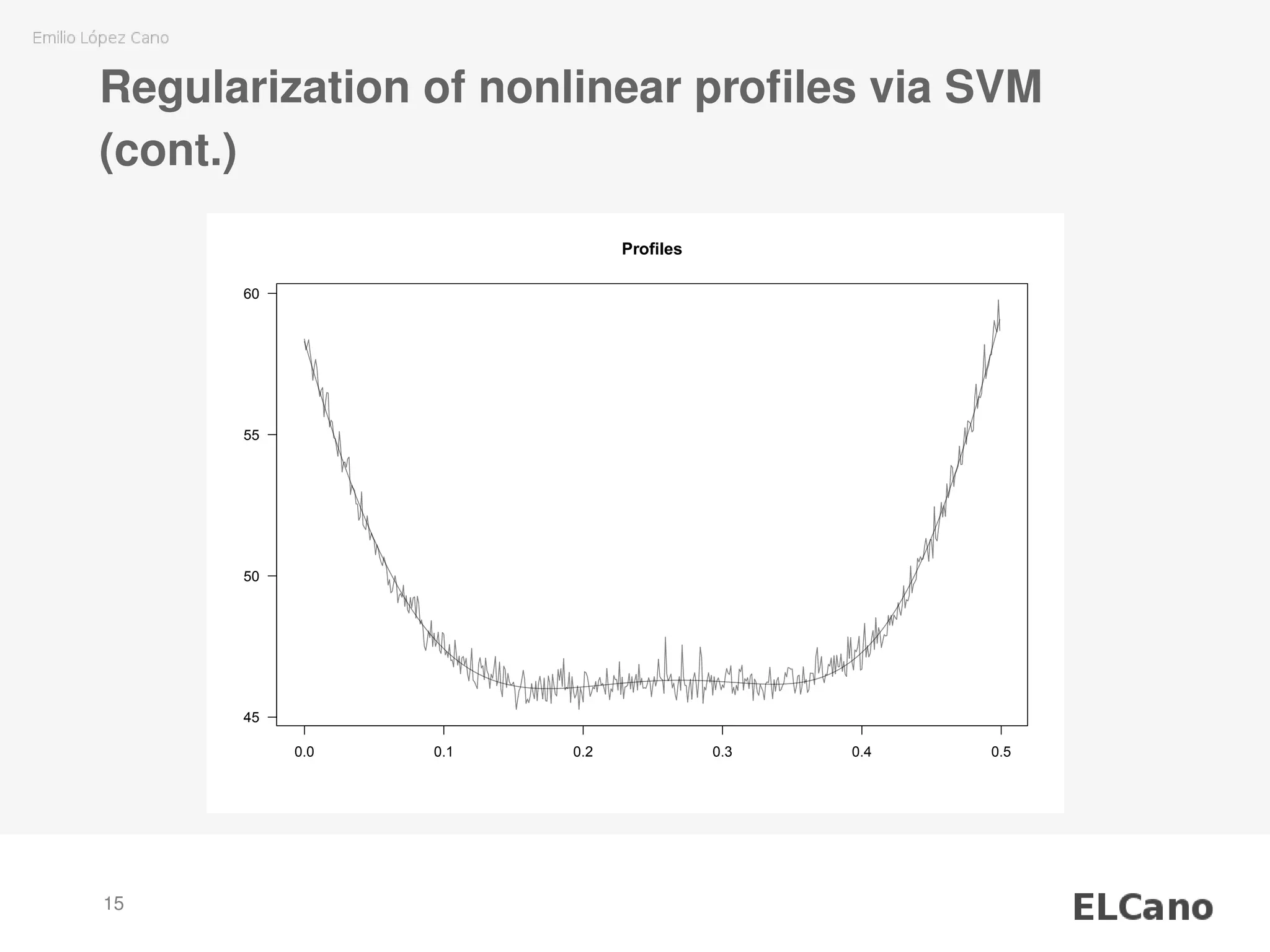
15. Regularization of nonlinear profiles via SVM
P1.smooth <- smoothProfiles(
profiles = ss.data.wby[, "P1"],
x = ss.data.wbx)
plotProfiles(profiles = cbind(P1.smooth,
ss.data.wby[, "P1"]),
x = ss.data.wbx)
14

16. Regularization of nonlinear profiles via SVM
(cont.)
0.0 0.1 0.2 0.3 0.4 0.5
45
50
55
60
Profiles
15

17. Smoothed prototype and confidence bands
0.0 0.1 0.2 0.3 0.4 0.5
40
45
50
55
60
65
Profiles

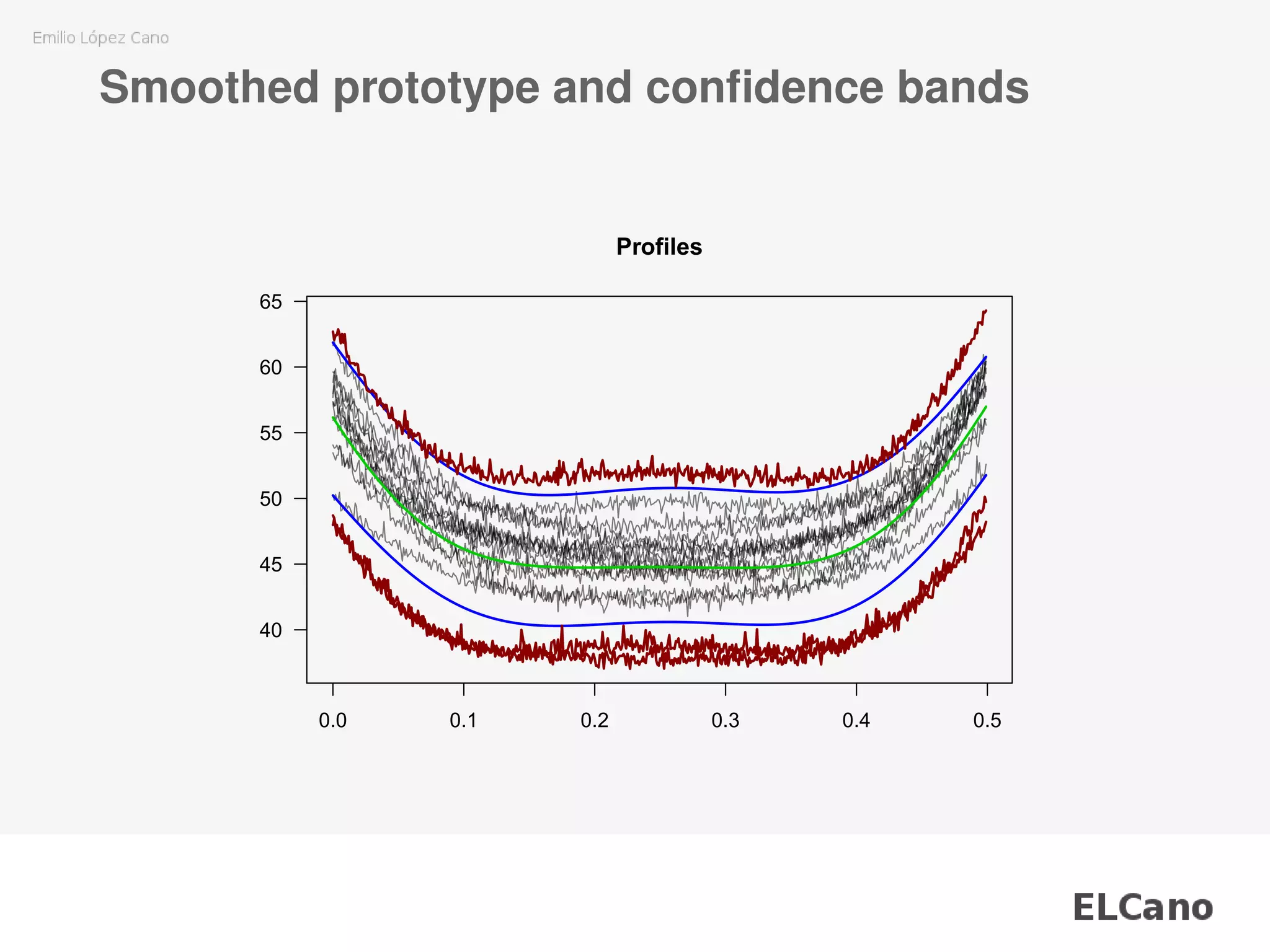
18. Smoothed prototype and confidence bands
(cont.)
wby.phase1 <- ss.data.wby[, 1:35]
wb.limits <- climProfiles(profiles = wby.phase1[, -28],
x = ss.data.wbx,
smoothprof = TRUE,
smoothlim = TRUE)
wby.phase2 <- ss.data.wby[, 36:50]
wb.out.phase2 <- outProfiles(profiles = wby.phase2,
x = ss.data.wbx,
cLimits = wb.limits,
tol = 0.8)
plotProfiles(wby.phase2,
x = ss.data.wbx,
cLimits = wb.limits,
outControl = wb.out.phase2$idOut,
onlyout = FALSE)

19. Questions
Thanks!
emilio.lcano@uclm.es
18