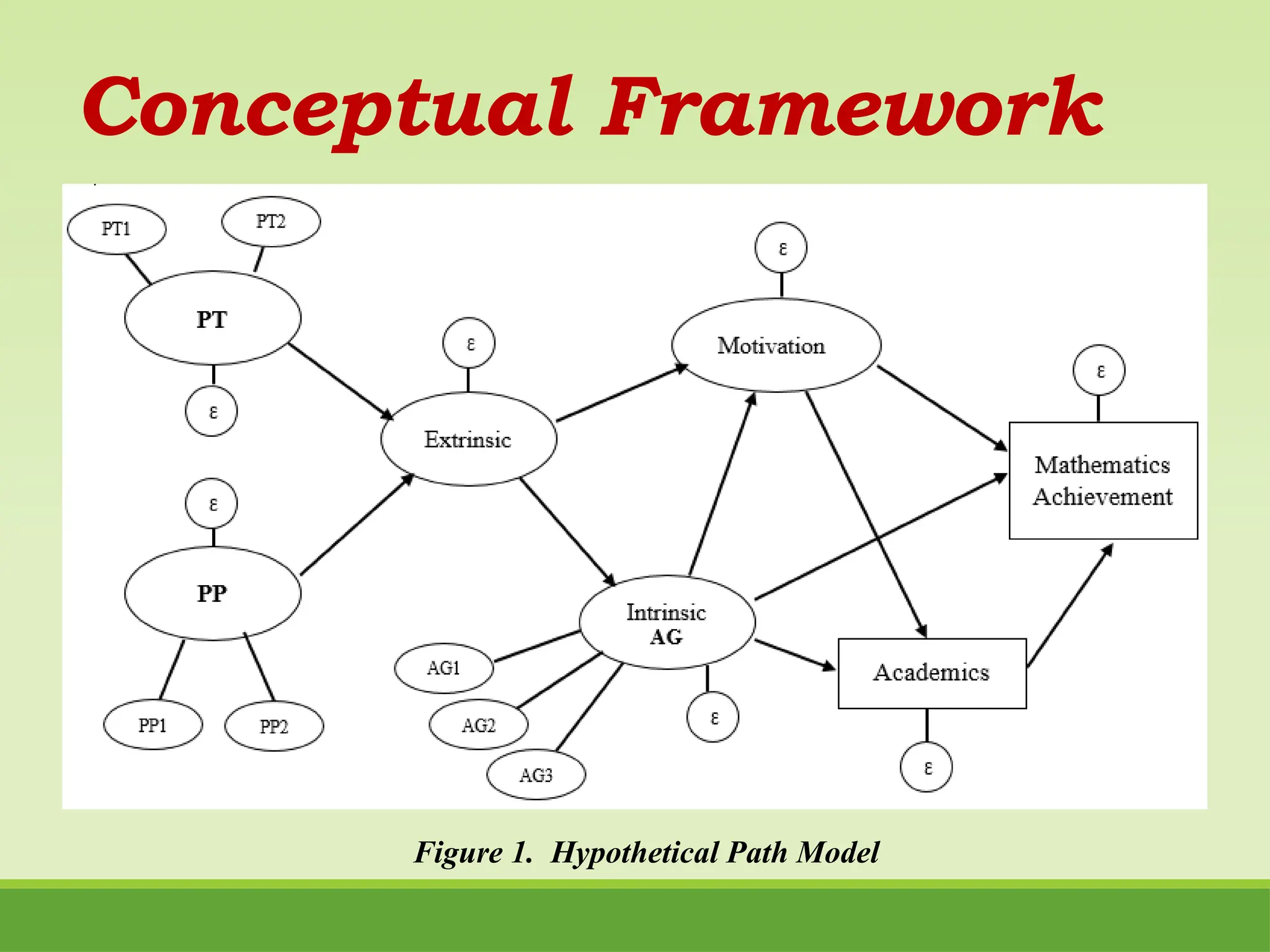
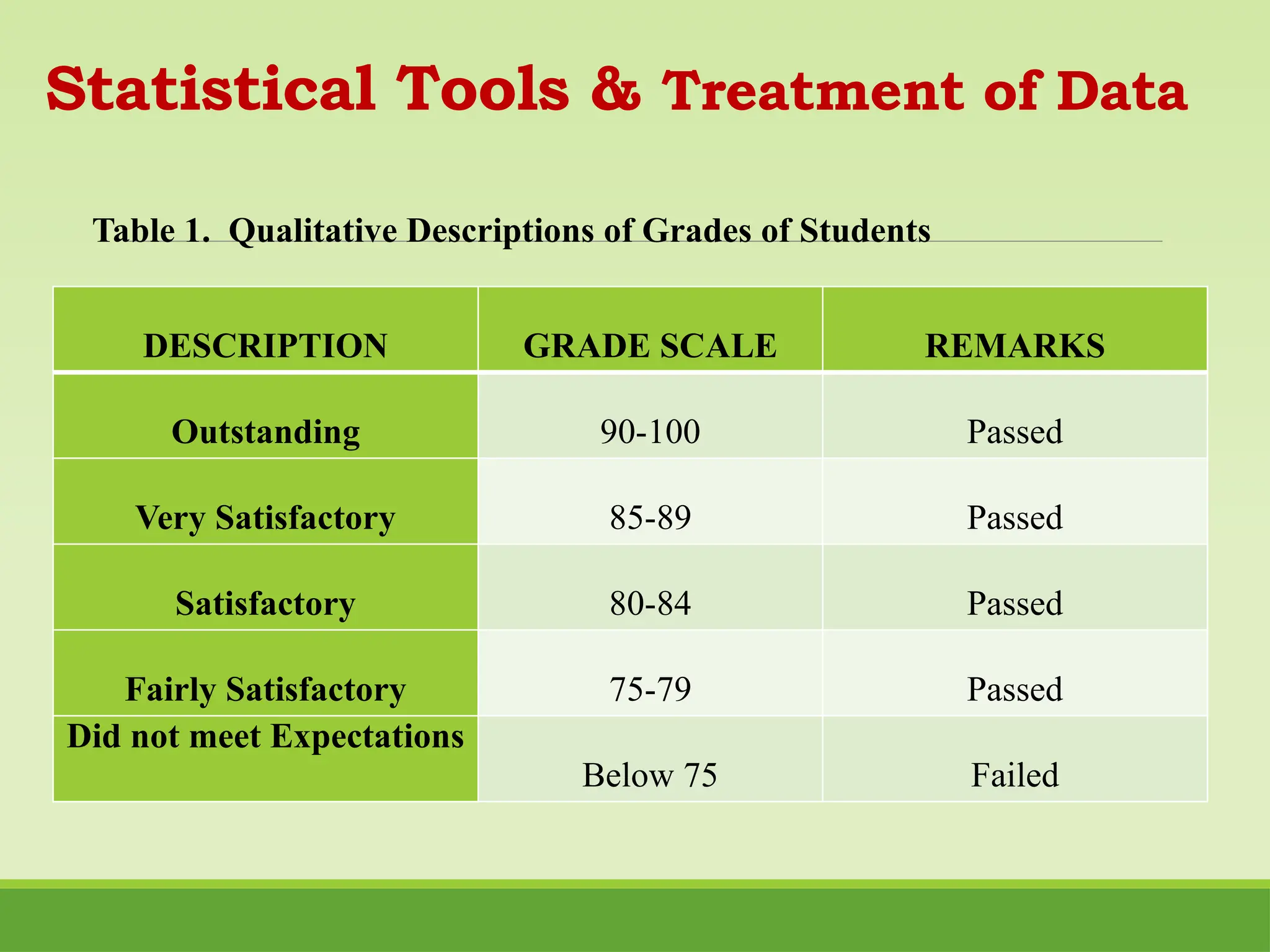
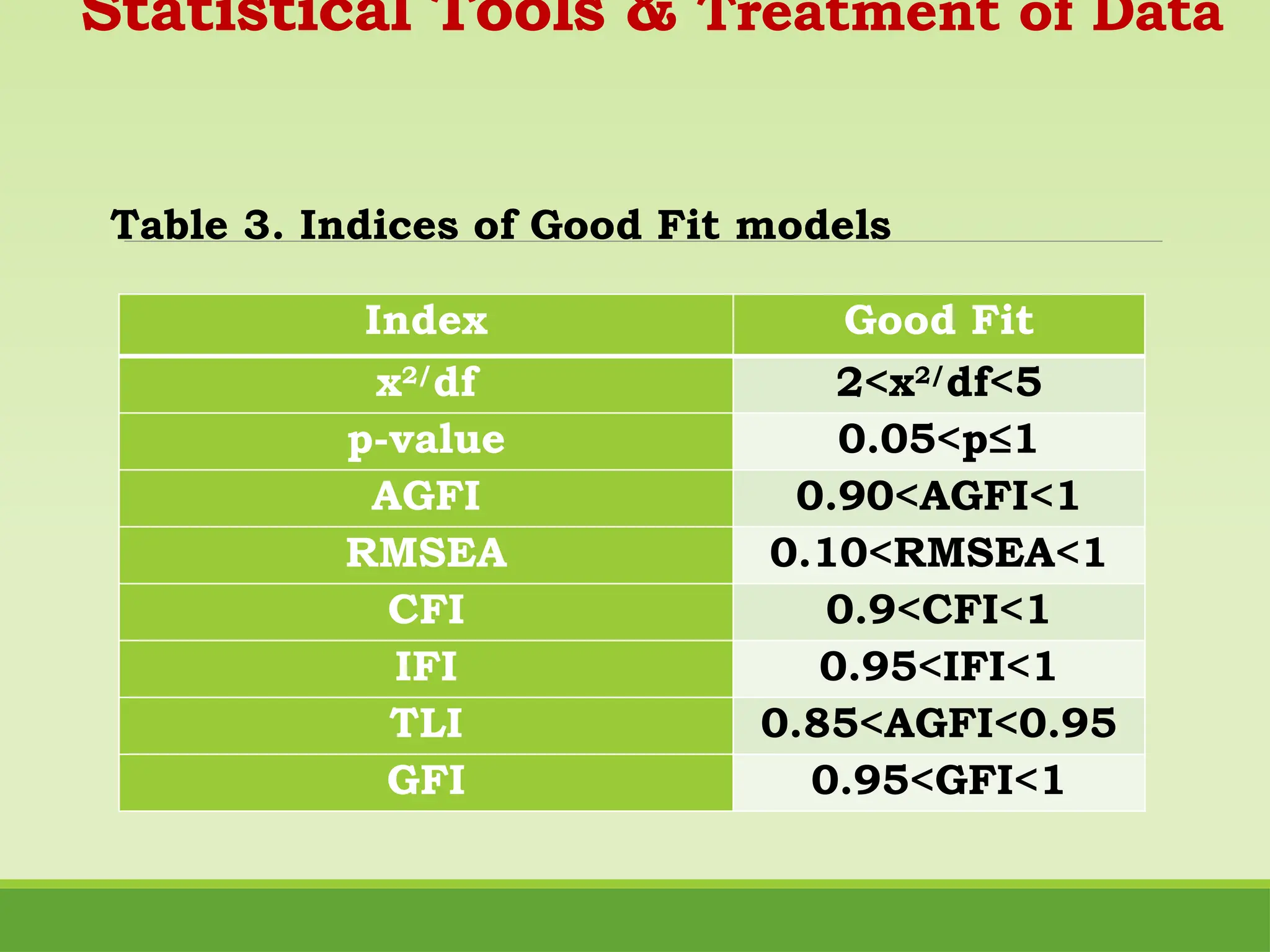
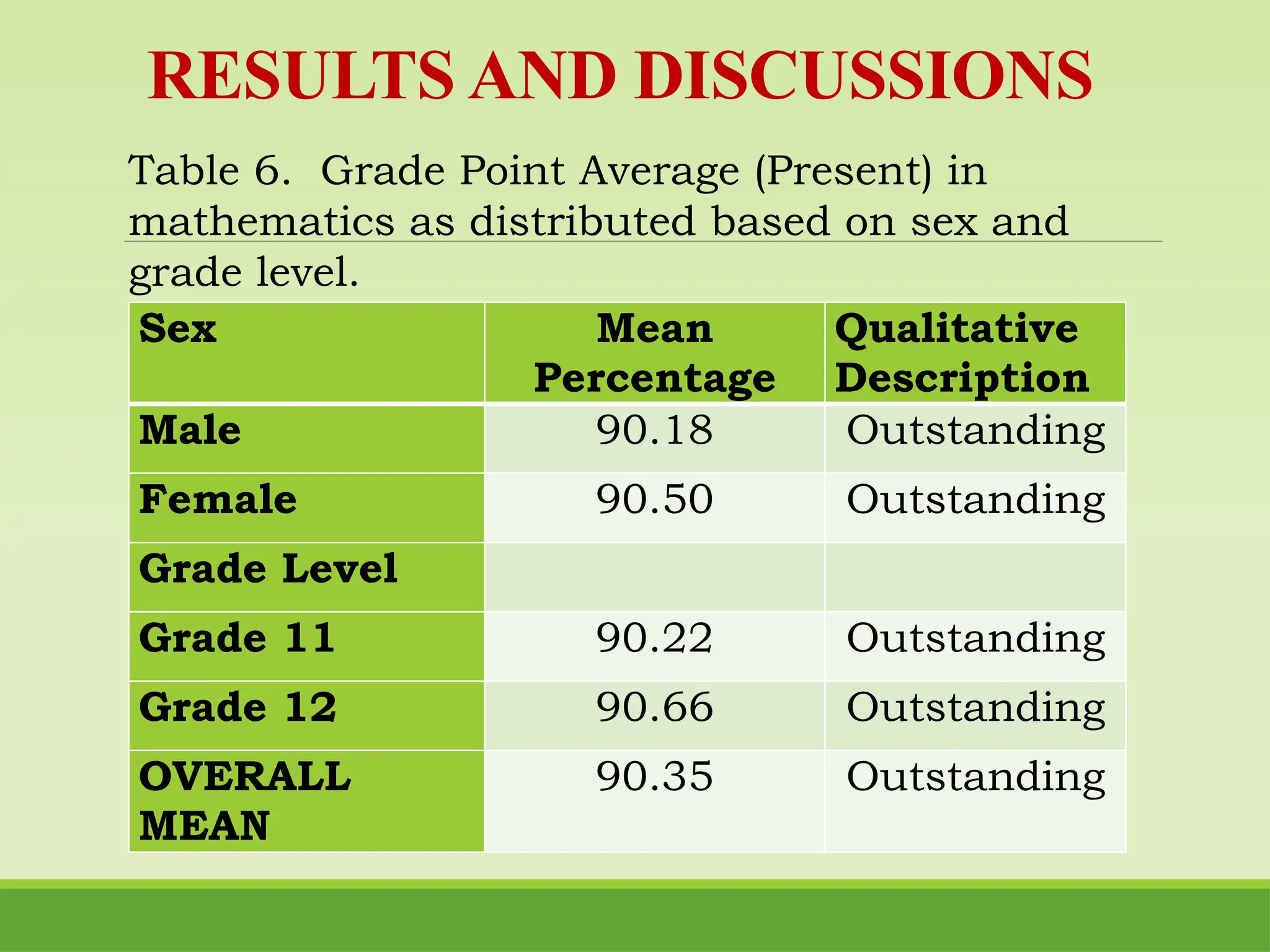
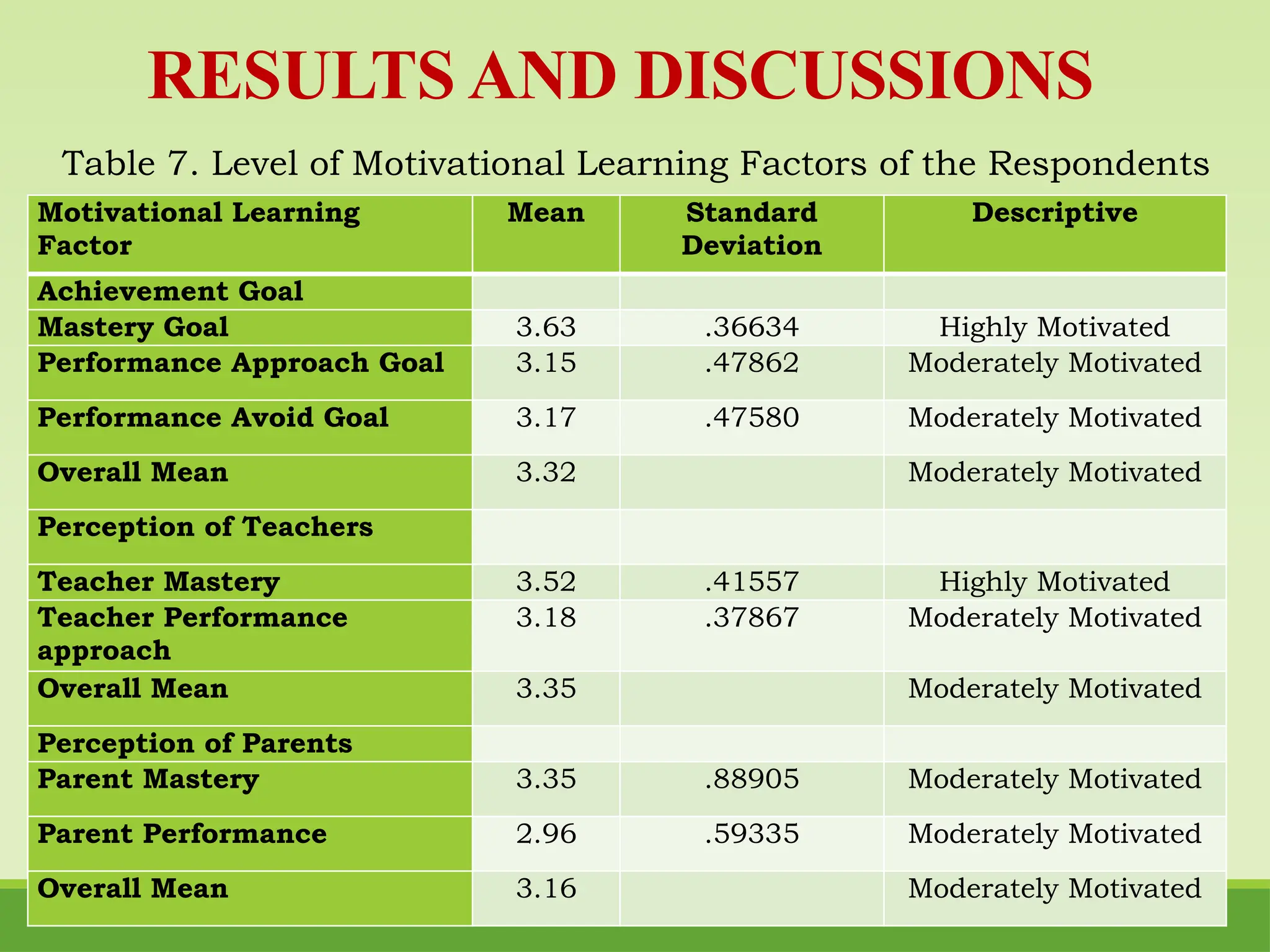
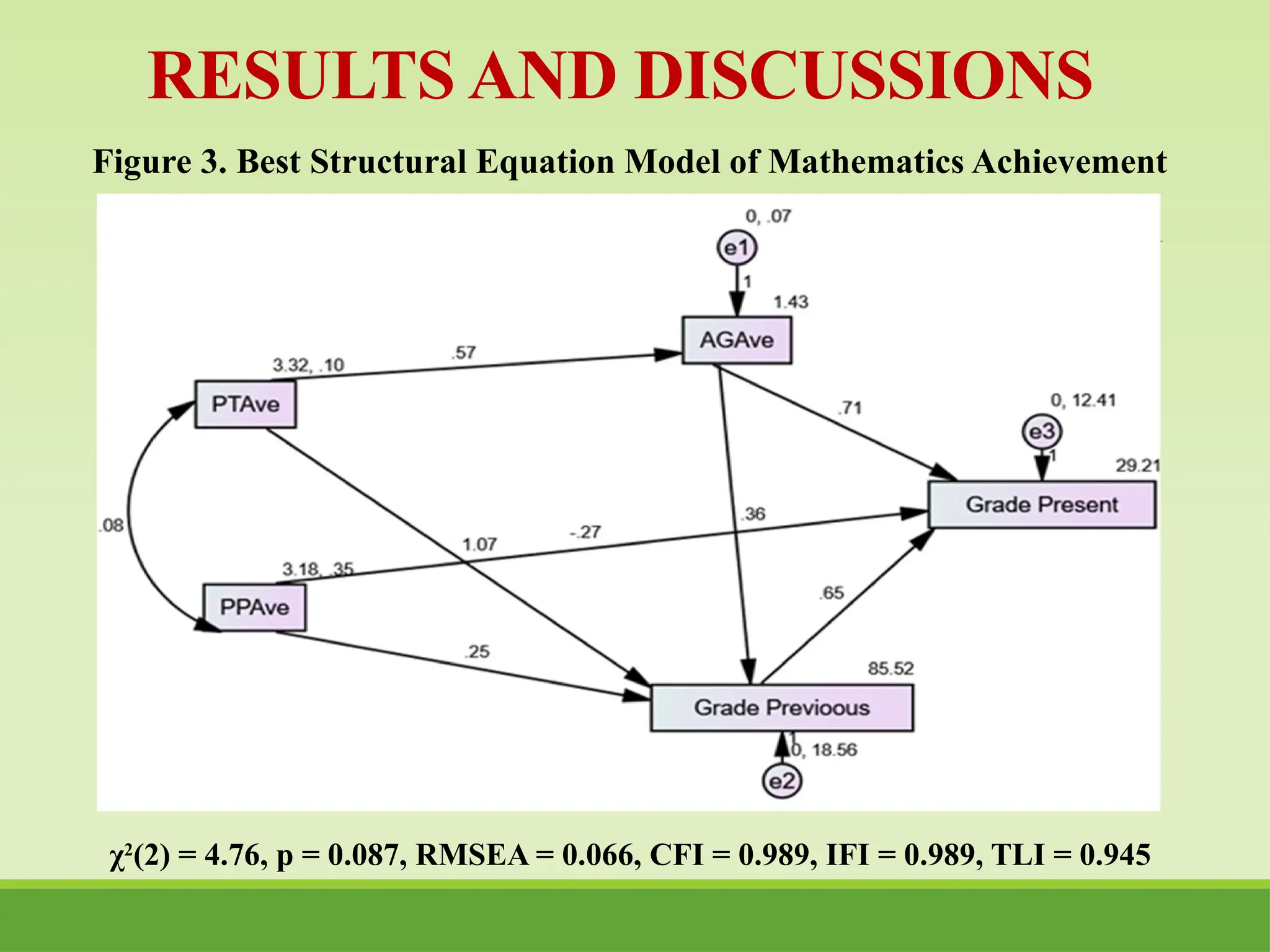
The study examines motivational learning factors and their impact on mathematics achievement among senior high school STEM students in Nueva Vizcaya, utilizing structural equation modeling. It identifies key variables such as students' academic goals and perceptions of teachers and parents, revealing a positive relationship between these factors and mathematics performance, while indicating a negative influence from parental perception. Recommendations include enhancing teacher training in motivational strategies and promoting parental involvement in mathematics education.

1. FINAL DEFENSE
WYNTEE MAY D VELASCO-CRUZ
MST-MATHEMATICS

2. MOTIVATIONAL LEARNING FACTORS AND MATHEMATICS
ACHIEVEMENT AMONG THE STEM-STRAND STUDENTS
OF THE DIVISION OF NUEVA VIZCAYA THROUGH
STRUCTURAL EQUATION MODELING

3. The Problem and Its Background
• Implementation of RA 10533 known as the
Enhanced Basic Education Curriculum
• The Importance of Mathematics as a
subject.
• Data on Mathematics Achievement
• Factors that affect Mathematics
achievement

4. Implementation of RA 10533 known as the
Enhanced Basic Education Curriculum
• Students are required 13 years of their
lives to stay in the school.
• 7 years in the Elementary Level
(Kindergarten to Grade 6).
• 6 years in the High School (4 years for the
Junior High School and 2 years for the
Senior High School)
• How to keep the learners motivated to
attend their classes for that long?

5. The Importance of Mathematics as a subject
• Provide opportunities for individuals to
develop skills and attitudes needed for
effective participation in everyday living
and prepare them for further education
and the world of work so that they make
worthwhile contributions to the society at
large (Pascua, 1993).
• Mathematics instruction has become a
basic need in all levels of education
• As teachers, how do we improve the
teaching-learning process to achieve
this goal?

6. Data on Mathematics Achievement
• Philippines ranked 58th
among the
participating countries based from TIMSS
ranked 2nd
lowest both in Mathematics
and scientific assessment in PISA 2018
( Mendoza, 2020);
• In the NAT, MPS in Math for Region 2 is
44.7, Division of Nueva Vizcaya is 42.27
while 47.8 for the 16 regions;
• How can we improve the Mathematics
Achievement in the National
Achievement Test (NAT)?

7. Factors that affect Mathematics Achievement
• Student-related and teacher-
related factors (Lubina, 2006; Del
Castillo (2010); Balbosa, 2010;
Yara, 2011);
• Environment factors and
psychological factors within the
learners like motivation (Kumar &
Karimi, 2010).

8. Factors that affect Mathematics Achievement
• According to Auwalu Shuaibu Muhammed,
et. al., 2014, it revealed that students’
academic performance is having a positive
relationship with their motivation in
learning.
• Acccording to Yazici and Altun (2013), the
importance of motivational sources may
decrease or increase according to the sample
group.
• How do these factors affect the
learning process and what is its effect
in the mathematics achievement?

9. Statement of the Problem
To address the goal of the Department of
Education K to 12 program that is, to strive
for excellence in mathematics, this study
aimed to determine a mathematical model
showing the interrelationships of the profile of
students, motivational learning factors that
determines mathematics achievement.

10. Objectives of the Study
This study aimed to determine the
mathematical model that will show interrelationships
of the students’ profile and motivational learning
factors to mathematics achievement.
Specifically, it sought to determine the
following:
1. To determine the demographic profile of the
learners in terms of the following:
a. Sex
b. Grade Level
c. Grade Point Average (GPA-previous grade).

11. Objectives of the Study
3. To determine the level of motivational learning
factors to students in terms of:
a. Achievement Goal
i. Mastery Goal
ii. Performance-Approach Goal
iii. Performance-Avoid Goal
b. Perception of Teachers
i. Teacher Mastery
ii. Teacher Performance-Approach
c. Perception of Parents
i. Parent Mastery
ii. Parent Performance
2. To determine the grade point average (GPA-present
grade) and the level of mathematics achievement of
the students,

12. Objectives of the Study
4. To determine the structural equation model that
reflects the interrelationships of student’s profile and
motivational learning factors to mathematics
achievement.

13. Scope and Limitation
The study focused primarily on the
motivational learning factors that affects students’
mathematics achievement in the mathematics
classroom. The motivational learning factors are
limited to the following namely; (a) Perception of
Teachers with aspects namely: Teachers’ Mastery and
Teachers’ Performance-Approach, (b) Perception of
Parents with aspects namely: Parents’ Mastery and
Parents’ Performance (c) Achievement Goal with
aspects namely: Mastery Goal, Performance-
Approach and Performance-Avoid Goal.

14. Scope and Limitation
The study will only include the senior high
school students enrolled in STEM-Strand from the
public schools under the Department of Education in
the Schools Division of Nueva Vizcaya. Deletion of
some indicators in the motivational learning factors
through factor loading was not realized by
Confirmatory Factor Analysis (CFA) since all the
items were considered good items as CFA was
applied. In addition, the questionnaire on
motivational learning factors is an adopted
questionnaire, thus all indicators of the learning
factors had been used in data analysis.

15. Conceptual Framework
Figure 1. Hypothetical Path Model

16. Research Design
This study utilized the descriptive and
exploratory designs of research. The descriptive type
of research was used to describe the student’s profile
and the level of mathematics achievement and the
level of motivational learning factors of the students.
The study explored the best mathematical model that
show interrelationships among student’s profile and
motivational learning factors that determines
mathematics achievement of senior students from the
STEM strand.

17. Time and Place of the Study
The study was conducted at the Public Senior
High Schools under the Department of Education in
the Schools Division of Nueva Vizcaya offering the
Science, Technology, Engineering and Mathematics
(STEM) Strand during the second semester of school
year 2018-2019. The Schools Division of Nueva
Vizcaya have 45 public high schools and of which 8
schools are offering STEM strand namely: Aritao
High School, Bambang High School, Diadi National
High School, Dupax del Norte National High School,
Nueva Vizcaya General Comprehensive High School,
Pinkian National High School, Runruno National High
School, and Solano High School.

18. Figure 2. Map of Nueva Vizcaya

19. Respondents of the Study
The respondents of the study were the grade 11
and 12 students from the identified public senior
high schools of the Schools Division of Nueva Vizcaya
enrolled in the STEM Strand during the second
semester of School Year 2018-2019. There were 34
students from Aritao High School, 75 students
Bambang High School, 28 students from Diadi
National High School, 20 students from Dupax del
Norte National High School, 102 students from Nueva
Vizcaya General Comprehensive High School, 20
students from Pinkian National High School,
23 students from Runruno National High School, and
48 students from Solano High School.

20. Respondents of the Study
However, only 330 students responded and
returned the fully answered questionnaire which were
used for further analysis. According to Wolf,
Harrington, Clark, and Miller (2013), the range of
sample size requirements for structural equation
modeling ranges from 30 to 460 cases. Thus, in this
study, 330 students was considered for data analysis.

21. Research Instrument
The respondents answered a questionnaire that
comprised of two parts. The first part was used to
determine students’ demographic profile (sex and
grade level, and previous and present grade point
average) while the second part was a questionnaire
on the Patterns of Adaptive Learning on the perceived
level of achievement goal, perception to teachers and
perception to parents. The questionnaire was
adopted from the Manual for the Patterns of Adaptive
Learning Scales (PALS revised) (Midgely, Maehr,
Hruda, Anderman, Andermanm, Freeman, Gheen et
al., 2000) with three identified motivational learning
factors.

22. Research Instrument
The first motivational learning factor is the
achievement goal comprised of three (3) aspects
which are Mastery Goal with five (5) items,
Performance-Approach goal with five (5) items and
Performance-Avoid goal with 4 items with Cronbach
Alpha of 0.85,.089 &0.74 respectively. The second
motivational learning factor is the Perception of
Teacher’s Goal with two (2) aspects which are
Teacher Mastery, 5 items and Teacher Performance-
Approach with 7 items with Cronbach Alpha of 0.83,
and 0.79 respectively.

23. The last motivational learning factor is the
Perceptions of Parents with 2 aspects which are
the Parent Mastery with 6 items and Parent
Performance with 5 items with Cronbach Alpha
0.71 for each aspect. Students was asked to rate
the following statement on a four-point Likert
scale (ranging from 1 as “strongly disagree’ to 4 as
“Strongly agree”). The 37 items were randomly
spread throughout the questionnaire, to avoid the
formation of possible reaction patterns. The said
questionnaire underwent expert validation for the
content of behavioral aspect by the expert
psychologists of the Nueva Vizcaya State
University identified by the panel.
Research Instrument

24. The grade point average (GPA-present) in
Mathematics of the participants was used to
represent their mathematics achievement and was
taken from their permanent school record (School
Form 10).
Research Instrument

25. Data Gathering Procedure
The process of data collection took place at the public
Senior High Schools of the Division of Nueva Vizcaya offering
Science, Technology, Engineering and Mathematics (STEM) Strand
namely Aritao High School, Bambang High School, Diadi National
High School, Dupax del Norte National High School, Nueva Vizcaya
General Comprehensive High School, Pinkian National High
School, Runruno National High School, and Solano High School.
A permit to conduct the research was secured from the
Office of the Superintendent of the Division and a letter to the
respective School Principals of the identified schools was endorsed
to gather data from their Grade 11 and 12 students which also
included their permit to access to their permanent records (SF 10)
for their grade point average (GPA).
Questionnaires that were the main tool of data collection
were distributed to the respondents by the researcher with the help
of their Mathematics teachers. A structured questionnaire was
distributed to a large number of male and female students

26. Statistical Tools & Treatment of Data
Descriptive statistics were used to
describe the demographic profile of the
participants and perceived level of the students
with regards to the identified motivational
learning factors. For the level of mathematics
achievement, the grade point average (GPA) of
the students will be described using the
descriptive scale as mention in Deped Order No.
8, s. 2015. Table 1 shows the qualitative
description of the grade point average of
students. The description will be as follows:

27. Statistical Tools & Treatment of Data
DESCRIPTION GRADE SCALE REMARKS
Outstanding 90-100 Passed
Very Satisfactory 85-89 Passed
Satisfactory 80-84 Passed
Fairly Satisfactory 75-79 Passed
Did not meet Expectations
Below 75 Failed
Table 1. Qualitative Descriptions of Grades of Students

28. Statistical Tools & Treatment of Data
Table 2. Qualitative Descriptions of Motivational Learning Factors
Weight Mean Range Description
4 3.51-4.50 Highly Motivated
3 2.51-3.50 Moderately Motivated
2 1.51-2.50 Fairly Motivated
1 1.00-1.50 Not Motivate

29. Statistical Tools & Treatment of Data
To describe the mathematical model that show
interrelationships among student’s profile and
motivational learning factors to the mathematics
achievement of students, Structural Equation
Modelling was employed (SEM) using Analysis of
Moment Structures (AMOS). SEM illustrates related
procedures in testing the interrelatedness of
observed statistics and unobserved variables.

30. Statistical Tools & Treatment of Data
Carlbäck & Wong (2018) stressed that chi-square
is one of the most reported absolute indices in
structural equation modeling. It explains the effect of
the numbers of variables considered in a study
wherein if more variables a model possesses, the
more likely the model will produce a higher chi-
square value. Several researchers have
recommended the range between 2.0 to 5.0 as a
general rule of thumb for acceptance of model fit
since there was a lack of universally agreed upon
standard regarding the value of an acceptable ratio.
Schermelleh-Engel & Moosbrugger (2003) stated
that the model is in good fit if p-value is greater
than 0.05 but less than or equal to 1.

31. Statistical Tools & Treatment of Data
Table 3. Indices of Good Fit models
Index Good Fit
x2/
df 2<x2/
df<5
p-value 0.05<p≤1
AGFI 0.90<AGFI<1
RMSEA 0.10<RMSEA<1
CFI 0.9<CFI<1
IFI 0.95<IFI<1
TLI 0.85<AGFI<0.95
GFI 0.95<GFI<1

32. A. Demographic Profile of the students in
terms of sex, grade level and grade in
the previous mathematics subject.
RESULTS AND DISCUSSIONS

33. RESULTS AND DISCUSSIONS
Table 4. Distribution of the respondents
based on sex and grade level
Sex Frequency Percent
Male 153 46.4
Female 177 53.6
Total 330 100
Grade Level
Grade 11 236 71.5
Grade 12 94 28.5
Total 330 100

34. RESULTS AND DISCUSSIONS
Table 5. Distribution of Grade Point Average (Previous)
according to sex and grade level of respondents
Sex Mean
Percentage
Qualitative
Description
Male 91.13 Outstanding
Female 91.02 Outstanding
Grade Level
Grade 11 91.11 Outstanding
Grade 12 90.96 Outstanding
OVERALL MEAN 91.07 Outstanding

35. B. Distribution of Grade Point Average
(Present) in Mathematics according to
sex and grade level.
RESULTS AND DISCUSSIONS

36. RESULTS AND DISCUSSIONS
Table 6. Grade Point Average (Present) in
mathematics as distributed based on sex and
grade level.
Sex Mean
Percentage
Qualitative
Description
Male 90.18 Outstanding
Female 90.50 Outstanding
Grade Level
Grade 11 90.22 Outstanding
Grade 12 90.66 Outstanding
OVERALL
MEAN
90.35 Outstanding

37. RESULTS AND DISCUSSIONS
C. Level of Motivational Factors towards
students mathematics achievement

38. RESULTS AND DISCUSSIONS
Table 7. Level of Motivational Learning Factors of the Respondents
Motivational Learning
Factor
Mean Standard
Deviation
Descriptive
Achievement Goal
Mastery Goal 3.63 .36634 Highly Motivated
Performance Approach Goal 3.15 .47862 Moderately Motivated
Performance Avoid Goal 3.17 .47580 Moderately Motivated
Overall Mean 3.32 Moderately Motivated
Perception of Teachers
Teacher Mastery 3.52 .41557 Highly Motivated
Teacher Performance
approach
3.18 .37867 Moderately Motivated
Overall Mean 3.35 Moderately Motivated
Perception of Parents
Parent Mastery 3.35 .88905 Moderately Motivated
Parent Performance 2.96 .59335 Moderately Motivated
Overall Mean 3.16 Moderately Motivated

39. RESULTS AND DISCUSSIONS
D. Optimal Structural Equation Model that reflects
the interrelationships of profile variables and
motivational learning factors to the academic
achievement of students.

40. RESULTS AND DISCUSSIONS
χ2
(2) = 4.76, p = 0.087, RMSEA = 0.066, CFI = 0.989, IFI = 0.989, TLI = 0.945
Figure 3. Best Structural Equation Model of Mathematics Achievement

41. SUMMARY, CONCLUSIONS AND
RECOMMENDATIONS
Summary
During the analysis of the study, the researcher tested a
structural equation model using SPSS and AMOS to explain the
motivational learning factor and mathematics achievement of the
STEM students of the Division of Nueva Vizcaya. Taking into
support on the model was investigated. The mathematical
achievement was examined based on the different motivational
learning factor such as the academic goal (AG Ave), perception of
the teachers (PT Ave) and the perception of the parent (PP Ave).
While testing the model, the AGAve and the grade previous had
explained a direct effect towards the mathematical achievement of
which the grade present. While the mathematical achievement of
the students showed a significant positive relationship. Moreover,
the perception of the teachers showed a significant relationship
towards grade previous and academic goal. However, perception
of the parents indicates a negative significant relationship. This
means that as one variable increases such as the perception of
parents increases, the grade present will decrease and vice versa.

42. Summary
In this study, the researcher investigated
grade previous, academic goal, perception of
teacher and perception of parents as main factors
that influence the motivational learning of the
students in their performance to learn
mathematics. Basing on the identified hypothesis
of this study was accepted and this finding was
consistent with previous researchers as stated in
this study. Students’ mathematical achievement
is captured based on the intrinsic motivational
learning factors based on their achieved academic
goal, perception of teachers in learning the subject
mathematics.
SUMMARY, CONCLUSIONS AND
RECOMMENDATIONS

43. CONCLUSIONS
Based on the significant findings of the study, the following
conclusions were drawn:
1. Grade 11 and 12 STEM students in the Department of
Education, Division of Nueva Vizcaya exhibited an outstanding
grades in mathematics during their previous semester and
present semester.
2. Grade 11 and 12 STEM students in the Department of
Education, Division of Nueva Vizcaya perceived that they are
moderately motivated to learn mathematics in terms of their
achievement goal, and support from their teachers and parents.
3. The structural equation model of mathematics achievement
includes the positive and indirect causal relationship of
motivation received by students from teachers and parents as
mediated by achievement goals of students as well as the first
semester grade, respectively however the direct causal effect of
the motivation from parents have a negative effect to the
mathematics achievement of students.
SUMMARY, CONCLUSIONS AND
RECOMMENDATIONS

44. SUMMARY, CONCLUSIONS AND
RECOMMENDATIONS
Recommendations
Based on the drawn conclusions, the following suggestive recommendations
must be considered as follows:
1. The study showed a significant performance of students in mathematics. This
further recommends monitoring and evaluating the best practices of the teachers
in teaching mathematics as well as the continuous upgrade of their professional
development.
2. This study further suggests that teachers may enhance their knowledge in the
field of motivation strategies in mathematics through attendance to seminars to
become more affective in developing greater interest of students to learn
mathematics.
3. School officials may device programs and projects that may help improve the role
of the parents in the delivery of learning in mathematics. It also further
recommends to conduct need analysis to determine the specific intervention that
can address the factor leading to the mathematical achievement of the students.
4. For future researchers, further studies may be conducted in terms of other
motivational learning factors that may affect the mathematics achievement of
students

45. THANK YOU