This document presents research on the feasibility of using radioisotope-based electron sources for space applications. It introduces two new types of space propulsion systems: the Minaka thruster and Kabila thruster. The Minaka thruster uses clusters of self-powered radioisotope cells to generate micro-newtons of thrust. It applies the principle of self-sufficiency to power the radioisotope electron sources. The Kabila thruster uses a hollow cathode with a radioisotope heat source instead of a conventional heater. It was found to save up to 3% in overall power compared to conventional ion thrusters. Both systems aim to overcome the energetic limitations of traditional space propulsion through novel use of radioisotopes

1. z中图分类号：V439
论 文 编号：10006LB1015202
基于电子源的放射性同位素
空间应用的可行性研究
作者姓名 伯易
学科专业 航空宇航推进理论与工程
指导教师 刘 宇 教授
培养学院 宇航学院
博 士 学 位 论 文

2. Feasibility Study of Radioisotope Based Electron
Sources for Space Applications
Candidate：Kalomba Mboyi
Supervisor：Pro. Liu Yu
School of Astronautics
Beihang University, Beijing, China

4. 中图分类号：V439
论 文 编号：10006LB1015202
博 士 学 位 论 文
基于电子源的放射性同位素空间应用
的可行性研究
作者姓名 伯易 申请学位级别 工学博士
指导教师姓名 刘 宇 职 称 教 授
学科专业 航空宇航推进理论与工程 研究方向 火箭发动机
学习时间自 2010年 9月 15日 起至 2015年 1月 30日 止
论文提交日期 2014年 3 月 01 日 论文答辩日期 2014年 6 月 10 日
学位授予单位 北京航空航天大学 学位授予日期 2015 年 1 月 26 日

6. 关于学位论文的独创性声明
本人郑重声明：所呈交的论文是本人在指导教师指导下独立进行研究工
作所取得的成果，论文中有关资料和数据是实事求是的。尽我所知，除文中
已经加以标注和致谢外，本论文不包含其他人已经发表或撰写的研究成果，
也不包含本人或他人为获得北京航空航天大学或其它教育机构的学位或学历
证书而使用过的材料。与我一同工作的同志对研究所做的任何贡献均已在论
文中作出了明确的说明。
若有不实之处，本人愿意承担相关法律责任。
学位论文作者签名： 日期： 年 月 日
学位论文使用授权书
本人完全同意北京航空航天大学有权使用本学位论文（包括但不限于其
印刷版和电子版），使用方式包括但不限于：保留学位论文，按规定向国家
有关部门（机构）送交学位论文，以学术交流为目的赠送和交换学位论文，
允许学位论文被查阅、借阅和复印，将学位论文的全部或部分内容编入有关
数据库进行检索，采用影印、缩印或其他复制手段保存学位论文。
保密学位论文在解密后的使用授权同上。
学位论文作者签名： 日期： 年 月 日
指导教师签名： 日期： 年 月 日

9. I
中文摘要
太空无疑是人类最后的边境，但其勘探并不是没有任何困难，因为它最大的障
碍是缺乏可利用的能源。空间飞行器必须携带的推进剂和能量转换系统的效率限制
了他们的最大工作范围。化学推进系统通过尽可能多地排放推进剂以达到稳定的地
球轨道，而电推进系统的推力水平则是受其动力装置生产能力的限制。因此，很少
能找到化学火箭持续燃烧时间超过几分钟，或者电推进系统的推力水平大于几牛顿。
常规的方法已被用来解决这一问题，目前为止，这个热门的短缺问题已通过提
高推进系统的效率来解决，并选择最合适的动力装置通过结构优化设计来节约能源。
由于通过进一步地大幅改进现有系统不太可能解决这一问题，因此应该寻求新的途
径。
这种解决方案可以在使用放射性同位素中被发现，并可通过一种基于自适应原
则的新方法来进行描述。它指出：“一个自适应的子系统是一个不需要系统内其他
子系统来实现其目的的”。自适应的子系统非常具有价值，因为它不需要任何能量
输入，甚至可以向其他子系统输出能量。一个子系统可以成为自适应系统存在两种
不同方式。其一，它可以自然地履行其角色，而不需要任何能量输入系统；其二，
它可以通过内部方法产生足够的能量来支撑其本身的运行。
自适应原则的应用导致了一种新的空间推进系统（放射微粒推进器）的发展，
即放射性同位素离子推进器。米娜卡和卡比拉推进器都属于这种新型的空间推进系
统，它们使用放射性同位素以一种新的方法克服了阻碍空间推进系统更好发展的能
量匮乏问题。
米娜卡推进器是一种新奇的空间推进系统，它使用自供能放射性同位素推进单
元(RPC)簇产生几微牛或几毫牛量级的推力。如果为每个RPC配备微型的朗缪尔探针
可以实现精确且均匀的推力矢量。被约束于永磁体或静电场的等离子体、放射性同
位素热电发生器(RTG)的电转换效率、电离度和放射性同位素密度等对米娜卡推进器
的性能产生了巨大的影响。自适应原则被用来估计RTG的放射性同位素电子源与放射
性同位素衰变热的功率。放射性同位素和电子减速过程会产生严重的辐射，并引起
质量的大幅增加。米娜卡推进器的应用取决于放射性同位素的半衰期，短半衰期的

10. II
放射性同位素适合用于自动转移运载器和地球观测卫星，而长半衰期的放射性同位
素则适合用于通信卫星和空间探测器。这种推进器的优点在于其能量储蓄功能、可
伸缩性和简洁性，但却比传统的离子推进器尺寸更大也更加危险。
本文还介绍了卡比拉阴极以及相应的推进器。卡比拉阴极是一种新型的空心阴
极，使用放射性同位素热源代替传统的铠装加热，而实现热离子发射的性能与传统
空心阴极类似。锶90、钚238和锔244被选为放射性同位素热源，而且热还原层也被
用来获取精确的热离子排放。空心阴极功率装置的加热器供给被RTG供给方式取代，
并且由于放射性同位素热源不能被切断而导致装置的操作模式也发生改变。这种空
心阴极经过与两个离子推进装置对比，发现其总功率最大能节省3%。它的优势在于
能量节约性能和可伸缩性，但却存在体积大、质量大和潜在危险等不足。卡比拉推
进器是一种新型的等离子体火箭发动机，它采用一种放射性同位素加热的加热室取
代了传统的燃烧室或催化床，其得到的比冲与传统的固体推进剂或双组元推进剂火
箭发动机类似。锔244被选为它的放射性同位素热源，热还原层被用来获取精确的热
离子排放。该火箭发动机和一个用于PleiadesHR1星座飞行器的1N肼推力器装置进行
对比，选用氦作为推进剂，其最大的比冲和功率分别能够节省529s和32%。这种火箭
发动机的优势在于能量节约性能、高比冲以及减少储量和再启动的同步性，然而与
卡比拉推进器类似，非常的占体积且存在危险性。
本文介绍了基于电子源的放射性同位素在空间应用的可行性，并且给出了辐射
推进器的发展状况。这打开了一个全新的、广阔的研究领域，还提出了许多的研究
方向。后续的研究工作应该从根本上去验证辐射推进器作为空间推进的备选方案的
可行性。
关键词：米娜卡，卡比拉，瑞迪恩，放射性同位素，贝塔负粒子，离子推进器，
自适应性，热电子发射体

11. III
Abstract
Space is unarguably humanity’s last frontier but its exploration has not been
without any difficulties because its greatest obstacle is the lack of exploitable
energy sources. Propellant and the efficiency of energy conversion systems that
spacecraft must carry along with them limit their maximal range of operation.
Chemical propulsion systems exhaust most of their propellant in order to reach
stable earth orbits and thrust levels achieved by electric propulsion systems are
limited by the production capacity of their power plants. It is thus rare to find
chemical rockets with continuous burning time exceeding several minutes or
electric propulsion systems with thrust levels greater than a few newtons.
Common methods used to solve this problem have been used and this energetic
scarcity problem has so far been tackled by improving the efficiency of propulsion
systems and by opting for the most appropriate power plants in order to save
energy through design optimization. Since further drastic improvements of
existing systems are unlikely, new ways to solve this energetic problem should
therefore be sought.
Such solution can be found in the use of radioisotopes. A new method addressing
this problem will now be presented. This new approach introduced by the author is
called the Self-Sufficiency Principle. It states that:”A self-sufficient subsystem is
one that does not require others to fulfil its purpose within its system.” Self-
sufficient subsystems are very useful because they do not require any power inputs
and can even output power into their system. A subsystem can become self-
sufficient in two different ways. It can either naturally fulfil its role hence does not
require any power input from its system or can through internal means produce
enough power to support its own operation.
The application of the Self-Sufficiency Principle led to the development of a new
kind of space propulsion systems named Radion thrusters, i.e.: Radioisotope
induced ion thrusters. The Minaka and Kabila classes of space propulsion systems
both belong to this new kind of space propulsion that uses radioisotopes in new
ways to overcome the energetic scarcity problem that hinders the development of
better space propulsion systems.

12. IV
The MINAKA thruster is a novel type of space propulsion systems that uses
clusters of self-powered radioisotope propulsive cells (RPC) to generate thrust
levels of the order of several micro and milli-newtons. Each cell was designed as
a micro discharge chamber with one anode wall, one acceleration grid and four
ionizing sides. Electrons emitted by from each ionizing sides were first decelerated
by an electron velocity modulator in order to achieve an optimal ionizing energy
before entering the discharge chamber where neutral gas ionizing would take
place. Plasma was also electrostatically confined by the downstream grids of the
electron velocity modulator. The Self-Sufficiency Principle was applied by
powering the radioisotope electron sources with the radioisotope decay heat using
a RTG. Radioisotopes and the electron deceleration process could generate
hazardous radiations and induce large mass increments. The application of the
MINAKA thruster depended on radioisotope half-lives and short half life
radioisotopes were found to be better suited to automated transfer vehicles and
earth observation satellites whilst long half life ones to communication satellites
and space probes. The advantages of the thruster were its power savings
capability, scalability and compactness but it was however found to be heavier and
more hazardous than conventional ion thrusters.
The Kabila cathode and rocket were also introduced in this research work. The
first one is a new type of hollow cathode using a radioisotope heat source instead
of a conventional sheathed heater and it achieved thermionic emission
performances similar to the ones of conventional hollow cathodes. Strontium-90,
Plutonium-238 and Curium-244 were chosen as radioisotope heat sources because
of their high decay heat. The heater supply of the hollow cathode power
configuration was replaced with a RTG supply and the mode of operation of the
device was modified because radioisotope heat sources cannot be switched off.
This hollow cathode was then benchmarked against two ion thruster
configurations and a maximal overall power saving of 3% was achieved. Its
advantages were its power saving capability and scalability but it could however
be voluminous, heavy and potentially hazardous. The Kabila rocket is a new type
of plasma rocket engine using a radioisotope heated thermionic heating chamber
instead of a conventional combustion chamber or catalyst bed. It achieved specific
impulses similar to the ones of conventional solid and bipropellant rockets.

13. V
Curium-244 was chosen as a radioisotope heat source. This rocket engine was then
benchmarked against a 1 N Hydrazine Thruster configuration operated on one of
the Pleiades-HR-1 constellation spacecraft. A maximal specific impulse and power
saving of respectively 529 seconds and 32% were achieved with helium as
propellant. Its advantages are its power saving capability, high specific impulses
and simultaneous ease of storage and restart. It can however just like the Kabila
rocket be extremely voluminous and potentially hazardous.
The feasibility of radioisotope based electron sources for space applications was
thus demonstrated and this research work led to the development of Radion
thrusters. This opened a totally new and extensive field of research and numerous
directions are now opened for investigation. Further work in this field should
ultimately attempt to validate Radion thrusters as viable space propulsion
alternatives.
Key words: minaka, kabila, plasma, radioisotope, beta minus, ion thruster, self-
sufficiency, thermionic

15. VII
Contents
1 Introduction ..............................................................................................................1
1.1 Space Propulsion Systems ...........................................................................................1
1.1.1 Chemical Propulsion Systems ..............................................................................1
1.1.2 Electric Propulsion Systems .................................................................................4
1.1.3 Nuclear Propulsion Systems .................................................................................9
1.1.4 Performance Comparison ...................................................................................11
1.2 Research Objective ....................................................................................................12
1.2.1 Problematic .........................................................................................................13
1.2.2 A New Approach: The Self-Sufficiency Principle .............................................14
1.2.3 Literature Survey ................................................................................................16
2 Background.............................................................................................................19
2.1 Power Generation.......................................................................................................19
2.2 Radiation Shielding Requirement ..............................................................................21
3 decay radioisotope electron source .................................................................25
3.1 Radioisotope Specific Activity ..................................................................................25
3.2 Electron Current Density ...........................................................................................25
3.3 Electron Velocity. ......................................................................................................27
3.4 Gas Ionization............................................................................................................28
3.5 Electron Velocity Modulation....................................................................................34
3.6 Gas Breakdown Voltage ............................................................................................36
3.7 Power Generation.......................................................................................................40
3.8 Application.................................................................................................................41
3.8.1 Ion thruster..........................................................................................................41

16. VIII
4 Radioisotope Heated Thermionic Electron Source ..............................................109
4.1 Thermionic Emission...............................................................................................109
4.2 Radioisotope.............................................................................................................107
4.3 Thermal Reductive Layer.........................................................................................111
4.4 Applications .............................................................................................................112
4.4.1 Hollow Cathode ................................................................................................112
4.4.2 Plasma Rocket Engine ......................................................................................124
Conclusion & Further Work..........................................................................................139
Conclusion ..........................................................................................................................139
Further Work.......................................................................................................................141
5 APPENDICES......................................................................................................143
Appendix A: Oopic Programming Script used to simulated the ionization process
inside the discharge chamber of the Minaka thruster .........................................................143
Appendix B: Numerical Data collected to plot the degree of ionization and thrust
density performance curves of the Minaka Thruster ..........................................................161
5.1.1 Neutral Gas Temperature = 300 C....................................................................161
5.1.2 Neutral Gas Temperature= 500C......................................................................166
5.1.3 Increasing Pressure from 1e-7 to 1e-1 [Torr] ...................................................171
References .....................................................................................................................175

17. IX
List of Diagrams
Diagram 1 chemical rocket combustion chamber and nozzle ...................................................1
Diagram 2 solid propellant rocket .............................................................................................2
Diagram 3 Solid propellant rocket grain geometries and corresponding thrust profiles ...........3
Diagram 4 monopropellant liquid rocket...................................................................................3
Diagram 5 bipropellant rocket engine .......................................................................................4
Diagram 6 DC discharge Ion Thruster.......................................................................................5
Diagram 7 RF Ion Thruster........................................................................................................5
Diagram 8 Microwave Ion Thruster ..........................................................................................6
Diagram 9 Arc jet ......................................................................................................................6
Diagram 10 Hall Thruster...........................................................................................................7
Diagram 11 Magneto Plasma Dynamic rocket (MPD)..............................................................8
Diagram 12 Variable Specific Impulse Magneto Plasma Dynamic rocket (VASIMR) ............9
Diagram 13 solid core nuclear reactor.....................................................................................10
Diagram 14 gas core nuclear reactor .......................................................................................10
Diagram 15: radioisotope thermal rocket (Poodle thruster) .....................................................11
Diagram 16 Radioisotope Thermoelectric Generator using the Seebeck Effect .....................19
Diagram 17 Radiation shielding illustration............................................................................21
Diagram 18 cubic volume of unit dimensions completely filled with radioisotope atoms ......26
Diagram 19 radioisotope electron current emitted from one side of a cubic volume of
unit dimensions.........................................................................................................................27
Diagram 20 Ionization and recombination processes ..............................................................29
Diagram 21 electron release during ionization process ...........................................................29

18. X
Diagram 22 Discharge chamber filled with neutral gas being ionized from its 4 sides by
radioisotope electron currents and neutral atoms and plasma being extracted from two of
its sides......................................................................................................................................32
Diagram 23 Electron ionization cross section of Xenon (5p orbit) .........................................34
Diagram 24 Electron velocity modulation using an electrostatic field....................................35
Diagram 25 Electric breakdown at atmospheric Pressure .......................................................37
Diagram 26 Vacuum dielectric breakdown .............................................................................37
Diagram 27 Breakdown voltage in xenon as a function of the product (p.d) [34] ..................39
Diagram 28 Thrust and degree of ionization achieved by for different numbers of
ionizing sides as a function of the discharge chamber length ..................................................47
Diagram 29 Thrust and degree of ionization achieved by for different numbers
of ionizing sides as a function of the discharge chamber length ..............................................47
Diagram 30 Thrust and degree of ionization achieved by for different numbers
of ionizing sides as a function of the discharge chamber length ..............................................48
Diagram 31 Thrust and degree of ionization achieved by for different numbers of
ionizing sides as a function of the discharge chamber length ..................................................48
Diagram 32 Thrust and degree of ionization achieved by for different numbers of
ionizing sides as a function of the discharge chamber length ..................................................49
Diagram 33 Thrust and degree of ionization achieved by for different numbers
of ionizing sides as a function of the discharge chamber length ..............................................49
Diagram 34 Thrust and degree of ionization achieved by for different numbers
of ionizing sides as a function of the discharge chamber length ..............................................50
Diagram 35 Thrust and degree of ionization achieved by for different numbers
of ionizing sides as a function of the discharge chamber length..............................................50
Diagram 36 Thrust and degree of ionization achieved by for different numbers
of ionizing sides as a function of the discharge chamber length ..............................................51
Diagram 37 Thrust and degree of ionization achieved by for different numbers
of ionizing sides as a function of the discharge chamber length ..............................................51

19. XI
Diagram 38 Thrust and degree of ionization achieved by for different numbers
of ionizing sides as a function of the discharge chamber length ..............................................52
Diagram 39 Thrust and degree of ionization achieved by for different numbers
of ionizing sides as a function of the discharge chamber length ..............................................52
Diagram 40 Thrust and degree of ionization achieved by for different numbers
of ionizing sides as a function of the discharge chamber length ..............................................53
Diagram 41 Thrust and degree of ionization achieved by for different numbers
of ionizing sides as a function of the discharge chamber length..............................................53
Diagram 42 Thrust and degree of ionization achieved by for different numbers
of ionizing sides as a function of the discharge chamber length ..............................................54
Diagram 43 Thrust and degree of ionization achieved by for different numbers
of ionizing sides as a function of the discharge chamber length ..............................................54
Diagram 44 Thrust density achieved by for different electric conversion
efficiencies as a function of the discharge chamber length ......................................................55
Diagram 45 Thrust density achieved by for different electric conversion
efficiencies as a function of the discharge chamber length ......................................................55
Diagram 46 Thrust density achieved by for different electric conversion
efficiencies as a function of the discharge chamber length ......................................................56
Diagram 47 Thrust density achieved by for different electric conversion
efficiencies as a function of the discharge chamber length ......................................................56
Diagram 48 Thrust density achieved by for different electric conversion
efficiencies as a function of the discharge chamber length ......................................................57
Diagram 49 Thrust density achieved by for different electric conversion
efficiencies as a function of the discharge chamber length......................................................57
Diagram 50 Thrust density achieved by for different electric conversion
efficiencies as a function of the discharge chamber length ......................................................58
Diagram 51 Thrust density achieved by for different electric conversion
efficiencies as a function of the discharge chamber length ......................................................58

20. XII
Diagram 52 Thrust density achieved by for different electric conversion
efficiencies as a function of the discharge chamber length ......................................................59
Diagram 53 Thrust density achieved by for different electric conversion
efficiencies as a function of the discharge chamber length ......................................................59
Diagram 54 Thrust density achieved by for different electric conversion
efficiencies as a function of the discharge chamber length ......................................................60
Diagram 55 Thrust and degree of ionization achieved by for different electric
conversion efficiencies as a function of the discharge chamber length....................................60
Diagram 56 Thrust density achieved by for different electric conversion
efficiencies as a function of the discharge chamber length ......................................................61
Diagram 57 Thrust density achieved by for different electric conversion
efficiencies as a function of the discharge chamber length ......................................................61
Diagram 58 Thrust density achieved by for different electric conversion
efficiencies as a function of the discharge chamber length ......................................................62
Diagram 59 Thrust density achieved by for different electric conversion
efficiencies as a function of the discharge chamber length ......................................................62
Diagram 60 Radioisotope mass and excess power densities achieved by as a
function of the discharge chamber length.................................................................................63
Diagram 61 Radioisotope mass and excess power densities achieved by as a
function of the discharge chamber length.................................................................................63
Diagram 62 Radioisotope mass and excess power densities achieved by as a
function of the discharge chamber length.................................................................................64
Diagram 63 Radioisotope mass and excess power densities achieved by as a
function of the discharge chamber length.................................................................................64
Diagram 64 Radioisotope mass and excess power densities achieved by as a
function of the discharge chamber length.................................................................................65
Diagram 65 Radioisotope mass and excess power densities achieved by as a
function of the discharge chamber length.................................................................................65

21. XIII
Diagram 66 Radioisotope mass and excess power densities achieved by as a
function of the discharge chamber length.................................................................................66
Diagram 67 Radioisotope mass and excess power densities achieved by as a
function of the discharge chamber length.................................................................................66
Diagram 68 Radioisotope mass and excess power densities achieved by as a
function of the discharge chamber length.................................................................................67
Diagram 69 Radioisotope mass and excess power densities achieved by as a
function of the discharge chamber length.................................................................................67
Diagram 70 Radioisotope mass and excess power densities achieved by as a
function of the discharge chamber length.................................................................................68
Diagram 71 Thrust and degree of ionization achieved by as a function of the
discharge chamber length .........................................................................................................68
Diagram 72 Radioisotope mass and excess power densities achieved by as a
function of the discharge chamber length.................................................................................69
Diagram 73 Radioisotope mass and excess power densities achieved by as a
function of the discharge chamber length.................................................................................69
Diagram 74 Radioisotope mass and excess power densities achieved by as a
function of the discharge chamber length.................................................................................70
Diagram 75 Radioisotope mass and excess power densities achieved by as a
function of the discharge chamber length.................................................................................70
Diagram 76 Minimal electric conversion efficiency of the selected radioisotopes .................71
Diagram 77 Thrust densities achieved by the radioisotopes of the first performance
group at their minimal electric conversion efficiency as a function of the discharge
chamber length..........................................................................................................................72
Diagram 78 Thrust densities achieved by the radioisotopes of the second performance
group at their minimal electric conversion efficiency as a function of the discharge
chamber length..........................................................................................................................72

22. XIV
Diagram 79 Thrust densities achieved by the radioisotopes of the third performance
group at their minimal electric conversion efficiency as a function of the discharge
chamber length..........................................................................................................................73
Diagram 80 Radioisotope mass density achieved by the first performance group at their
minimal electric conversion efficiency as a function of the discharge chamber length...........73
Diagram 81 Radioisotope mass density achieved by the second performance group at
their minimal electric conversion efficiency as a function of the discharge chamber
length ........................................................................................................................................74
Diagram 82 Radioisotope mass density achieved by the third performance group at their
minimal electric conversion efficiency as a function of the discharge chamber length...........74
Diagram 83 Excess power density achieved by the first performance group at their
minimal electric conversion efficiency as a function of the discharge chamber length...........75
Diagram 84 Excess power density achieved by the second performance group at their
minimal electric conversion efficiency as a function of the discharge chamber length...........75
Diagram 85 Excess power density achieved by the third performance group at their
minimal electric conversion efficiency as a function of the discharge chamber length...........76
Diagram 86 Specific thrust achieved by the first performance group at their minimal
electric conversion efficiency as a function of the discharge chamber length .........................76
Diagram 87 Specific thrust achieved by the second performance group at their minimal
electric conversion efficiency as a function of the discharge chamber length .........................77
Diagram 88 Specific thrust achieved by the third performance group at their minimal
electric conversion efficiency as a function of the discharge chamber length .........................77
Diagram 89 Specific excess power achieved the first performance group at their
minimal electric conversion efficiency as a function of the discharge chamber length...........78
Diagram 90 Specific excess power achieved the second performance group at their
minimal electric conversion efficiency as a function of the discharge chamber length...........78
Diagram 91 Specific excess power achieved the third performance group at their
minimal electric conversion efficiency as a function of the discharge chamber length...........79

23. XV
Diagram 92 Power Configuration and geometry of a Radioisotope Electron Source
(RES) ........................................................................................................................................81
Diagram 93 Geometry of a Radioisotope Propulsive Cell (RPC) based on which the
thrust, radioisotope mass and excess power densities are calculated .......................................81
Diagram 94 Operation of a Radioisotope Propulsive Cell (RPC) ...........................................82
Diagram 95 Deployment of RPC panels fitted on a communication satellite .........................83
Diagram 96 geometry of the Minaka Discharge chamber .......................................................96
Diagram 97 Example of a 2D particle diagnostic plot ............................................................97
Diagram 98 Example of a 3D particle distribution diagnostic plot .........................................97
Diagram 99 Example of a plot representing the time variation of the number of
simulated particles ....................................................................................................................98
Diagram 100 Uniform ionization pattern inside the Minaka thruster discharge chamber ....100
Diagram 101 plot of electron count over time (blue line) .....................................................101
Diagram 102 uniform ion density..........................................................................................101
Diagram 103 constant ion production rate (green line) .........................................................102
Diagram 104 variation the degree of ionization achieved by Tm-171 with discharge
chamber length using different models and at different neutral gas temperatures .................104
Diagram 105 variation the thrust density of Tm-171 with discharge chamber length
using different models and at different neutral gas temperatures ...........................................105
Diagram 106 Variation of the degree of ionization and thrust density with the neutral
gas pressure.............................................................................................................................105
Diagram 107 Exponential growth profile of the ion count in electron confined
ionization model .....................................................................................................................106
Diagram 108 Linear and uninterrupted growth profile of the electron count in electron
confined ionization model ......................................................................................................107
Diagram 109 thermionic emission of a light bulb .................................................................109
Diagram 110 Emission current density versus temperature for various cathode
materials[2] .............................................................................................................................107

24. XVI
Diagram 111 thermal conduction between a heat source (dark grey) and an emitter
material (light grey) through a thermal reductive layer (diagonals) of a given thickness
and thermal conductivity ........................................................................................................112
Diagram 112 Simplified representation of the emitter segment of the hollow cathode
tube and of the radioisotope heat source where the emitter length, , cathode tube, ,
and radioisotope heater diameter, , are indicated..............................................................114
Diagram 113 Schematic of a conventional[2] (a) and Kabila (b) cathode showing the
cathode tube, insert, heater enclosed and RTG module in an on/off mode enclosed in a
keeper electrode ......................................................................................................................122
Diagram 114 Electrical schematic of a conventional DC-discharge ion thruster[2] (a)
and of one using a Kabila cathode (b) with the cathode heater, keeper, RTG and
discharge power supplies........................................................................................................123
Diagram 115 Converging-diverging nozzle configuration....................................................124
Diagram 116 Schematic of the Radioisotope Heated Plasma Rocket Engine .......................126
Diagram 117 Radioisotope heated thermionic heater chamber versus the thrust
generated with different neutral gases ....................................................................................131
Diagram 118 Radioisotope heated thermionic plasma rocket engine specific impulse
versus the exhaust velocity with different neutral gases ........................................................132
Diagram B1 Ion count plot for Tn=300C Ld=1cm, macro-to-real particle=1e3 and x3=1
m .............................................................................................................................................161
Diagram B2 Ion count plot for Tn=300C Ld=2cm, macro-to-real particle=1e3 and x3=1
m .............................................................................................................................................161
Diagram B3 Ion count plot for Tn=300C Ld=3cm, macro-to-real particle=1e4 and x3=1
m .............................................................................................................................................162
Diagram B4 Ion count plot for Tn=300C Ld=4cm, macro-to-real particle=1e5 and x3=1
m .............................................................................................................................................162
Diagram B5 Ion count plot for Tn=300C Ld=5cm, macro-to-real particle=1e5 and x3=1
m .............................................................................................................................................163

25. XVII
Diagram B6 Ion count plot for Tn=300C Ld=6cm, macro-to-real particle=1e5 and x3=1
m .............................................................................................................................................163
Diagram B7 Ion count plot for Tn=300C Ld=7cm, macro-to-real particle=1e5 and x3=1
m .............................................................................................................................................164
Diagram B8 Ion count plot for Tn=300C Ld=8cm, macro-to-real particle=1e5 and x3=1
m .............................................................................................................................................164
Diagram B9 Ion count plot for Tn=300C Ld=9cm, macro-to-real particle=1e5 and x3=1
m .............................................................................................................................................165
Diagram B10 Ion count plot for Tn=300C Ld=10cm, macro-to-real particle=1e5 and
x3=1 m....................................................................................................................................165
Diagram B11 Ion count plot for Tn=500C Ld=1cm, macro-to-real particle=1e3 and
x3=1 m....................................................................................................................................166
Diagram B12 Ion count plot for Tn=500C Ld=2cm, macro-to-real particle=1e3 and
x3=1 m....................................................................................................................................166
Diagram B13 Ion count plot for Tn=500C Ld=3cm, macro-to-real particle=1e4 and
x3=1 m....................................................................................................................................167
Diagram B14 Ion count plot for Tn=500C Ld=4cm, macro-to-real particle=1e5 and
x3=1 m....................................................................................................................................167
Diagram B15 Ion count plot for Tn=500C Ld=5cm, macro-to-real particle=1e5 and
x3=1 m....................................................................................................................................168
Diagram B16 Ion count plot for Tn=500C Ld=6cm, macro-to-real particle=1e5 and
x3=1 m....................................................................................................................................168
Diagram B17 Ion count plot for Tn=500C Ld=7cm, macro-to-real particle=1e5 and
x3=1 m....................................................................................................................................169
Diagram B18 Ion count plot for Tn=500C Ld=8cm, macro-to-real particle=1e6 and
x3=1 m....................................................................................................................................169
Diagram B19 Ion count plot for Tn=500C Ld=9cm, macro-to-real particle=1e6 and
x3=1 m....................................................................................................................................170

26. XVIII
Diagram B20 Ion count plot for Tn=500C Ld=10cm, macro-to-real particle=1e6 and
x3=1 m....................................................................................................................................170
Diagram B21 Ion count plot for Tn=300C and Pres= 1e-1 [Torr] Ld=1cm, macro-to-real
particle=1e3 and x3=1 m ........................................................................................................171
Diagram B22 Ion count plot for Tn=300C and Pres= 1e-2 [Torr] Ld=1cm, macro-to-real
particle=1e3 and x3=1 m ........................................................................................................171
Diagram B23 Ion count plot for Tn=300C and Pres= 1e-3 [Torr] Ld=1cm, macro-to-real
particle=1e3 and x3=1 m ........................................................................................................172
Diagram B24 Ion count plot for Tn=300C and Pres= 1e-4 [Torr] Ld=1cm, macro-to-real
particle=1e3 and x3=1 m ........................................................................................................172
Diagram B25 Ion count plot for Tn=300C and Pres= 1e-5 [Torr] Ld=1cm, macro-to-real
particle=1e3 and x3=1 m ........................................................................................................173
Diagram B26 Ion count plot for Tn=300C and Pres= 1e-6 [Torr] Ld=1cm, macro-to-real
particle=1e3 and x3=1 m ........................................................................................................173
Diagram B27 Ion count plot for Tn=300C and Pres= 1e-7 [Torr] Ld=1cm, macro-to-real
particle=1e2 and x3=1 m ........................................................................................................174

27. List of Tables
Table 1 Performance characteristics of different space propulsion systems ...........................12
Table 2 Radioisotope Data.......................................................................................................46
Table 2 Radioisotope Data (continued) ...................................................................................46
Table 2 Radioisotope Data (continued) ...................................................................................47
Table 2 Radioisotope Data (continued) ...................................................................................47
Table 3 Radioisotope production processes and ease..............................................................91
Table 4 Approximate lead shielding required for radioisotope sources for
at ................................................................................................................94
Table 5 Simulation Parameters for Thulium-171 induced neutral gas ionization ...................99
Table 6 Work Function and Richardson coefficients for several cathode materials[2] ........111
Table 7 Radioisotope characteristics and lead shielding required for
radioisotope sources for a target exposure of at [39]............................109
Table 8 Thermionic emission current densities for Strontium-90, Plutonium-238 and
Curium-244 using different insert materials...........................................................................109
Table 9 Power and geometric characteristics of the NSTAR-TH15 and of the NEXIS-
MAX configurations...............................................................................................................117
Table 10 Performance characteristics of the radioisotope heated hollow cathodes when
applied to the NSTAR-TH15 and NEXIS-MAX configurations ...........................................117
Table 11 ISPs and Combustion Chamber Temperatures of Conventional Rocket
Engines [2]..............................................................................................................................125
Table 12 Data of the 1 N Hydrazine Thruster configuration [51] .........................................128
Table 13 NSTAR-TH15 Data................................................................................................128
Table 14 Noble Gas Data......................................................................................................129
Table 15 Power Related Data ................................................................................................129
Table 16 Mass Flow Rate Performances ...............................................................................129
Table 17 Power Performances ...............................................................................................131

28. II

29. XXI
Nomenclature
MPD Magneto Plasma Dynamic Rocket
VASIMR Variable Specific Impulse Magneto Plasma Rocket
electrical efficiency of ion thrusters,
beam power,
total power input,
beam current,
beam voltage,
other power inputs,
discharge power,
cathode keeper power,
neutralizer cathode power,
acceleration grid power,
Beta minus (decay radioisotope)
RHU Radioisotope Heater Unit
RTG Radioisotope Thermoelectric Generator
REP Radioisotope Electric Propulsion
MHD Magneto HydroDynamic
electric power generated by a RTG,
thermal conversion efficiency,
radioisotope mass,
radioisotope specific heat, ⁄
radioisotope decay energy,

30. XXII
radioisotope decay constant, ⁄
Avogadro’s number, ⁄
atomic weight,
⁄ half life of the radioisotope,
shielded exposure, ⁄
unshielded exposure, ⁄
linear attenuation coefficient, ⁄
radiation shielding thickness,
gamma factor,
equivalent activity,
radioisotope specific activity,
equivalent radioisotope mass,
target thermal power,
mass attenuation coefficient,
shielding material density,
radioisotope density per unit volume,
radioisotope number density,
radioisotope density,
activity density in any given direction,
radioisotope current density, ⁄
electron charge,
kinetic energy,
particle mass,
particle velocity,

31. XXIII
mean decay energy,
Lorentz factor,
speed of light, ⁄
rate of production of ion-electron through gas ionization,
neutral gas density,
primary electron density,
electron ionization cross section,
primary electron velocity, ⁄
discharge chamber volume,
secondary electron density,
secondary electron velocity, ⁄
radioisotope electron current density, ⁄
unit volume,
total radioisotope current,
unit surface area,
number of ionizing sides,
surface area of one of the discharge chamber’s side,
discharge chamber length,
degree of ionization,
EVM Electron Velocity Modulator
difference in kinetic energy,
final kinetic energy,
initial kinetic energy,
final velocity,

32. XXIV
initial velocity,
power required to modulate the velocity of a given
number of electrons,
̇ electron flow rate,
electric power,
current,
voltage,
electron modulator voltage,
breakdown voltage,
gas specific breakdown voltage constant ,
pressure,
gap distance,
gas specific breakdown voltage constant,
gas specific breakdown voltage constant,
gas specific breakdown voltage constant,
vacuum dielectric breakdown voltage constant, ⁄
equivalent radioisotope mass,
thickness of the radioisotope electron source,
Thrust,
propellant atomic mass,
ion density,
acoustic velocity,
grid surface area,
grid transparency,
Boltzmann’s constant, ⁄

33. XXV
electron temperature,
ion mass,
remaining power,
MINAKA Micheline Nathalie Kapinga
RPC radioisotope propulsive cell
RES radioisotope electron source
ATV Automated Transfer Vehicles
EOS Earth Observation Satellites
Thermionic emission density, ⁄
thermionic emission constant, ⁄
thermionic emission temperature,
work function,
thermionic emission constant, ⁄
conductive heat transfer,
thermal conductivity of the thermal reductive layer,
⁄⁄
temperature of the hot surface,
temperature of the cold surface,
thickness of the thermal reductive layer,
surface area,
heat flux, ⁄
discharge cathode keeper current,
discharge cathode keeper voltage,
radioisotope power generated per unit mass, ⁄
required radioisotope mass,

34. XXVI
required radioisotope volume,
emitter length,
cathode tube diameter,
radioisotope heater diameter,
NSTAR Nasa Solar Electric Propulsion Application Readiness
NEXIS Nuclear Electric Xenon Ion System
Thruster Diameter,
, Thruster’s mass,
Total Engine Power,
Kabila
Laurent-Désiré Kabila, hero and former president of the
Democratic Republic of Congo
̇ mass flow rate, ⁄
exhaust velocity, ⁄
ISP specific impulse,
specific impulse,
earth gravitational acceleration, ⁄
ratio of specific heat,
specific gas constant, ⁄⁄
combustion chamber’s temperature,
̇ mass flow rate density, ⁄⁄
̇ mass flow rate through the emitter, ⁄
insert surface area,
radioisotope thermionic heating chamber’s diameter,
̇ target mass flow rate, ⁄

35. BUAA Academic Dissertation for Doctoral
1
1 Introduction
1.1 Space PropulsionSystems
Space propulsion systems have enabled the exploration of space. These come in
different sorts, i.e.: chemical, electric and nuclear propulsion systems, and each
sort has its own applications and performance characteristics. These propulsion
systems will now be introduced in this section.
1.1.1 Chemical Propulsion Systems
Chemical propulsion systems use exothermic chemical reactions to generate high
levels of thrust. Propellants are first heated up in a combustion chamber where
their gas pressure is raised with increasing temperature and then extracted through
a nozzle to generate thrust. Both processes are illustrated below in Diagram 1.
Chemical propulsion systems use different types of propellant, i.e.: solid or liquid
propellants, and each type of propellant has different set of advantages and
drawbacks.
Diagram 1 chemical rocket combustion chamber and nozzle

36. Chapter 1 Introduction
2
1.1.1.1 Solid Propellant
Solid propellant rockets, illustrated in Diagram 2, ignite a solid propellant to
generate thrust. This propellant is pasted inside the discharge chamber and is
ignited using an igniter. Once the propellant has been ignited, the combustion
process cannot be easily stopped which limits the application of solid propellant
rockets to complete burnout situations. They can therefore not be used as satellite
thrusters and are primarily used on missiles because of their high specific
impulses.
Diagram 2 solid propellant rocket
Propellant grain geometry has a great impact on solid propellant rockets
performances because it determines the thrust profile of the rocket. Different grain
geometries are illustrated in Diagram 3. It can be seen that sharp decreasing,
increasing and even continuous thrust profiles can be obtained using different
types of grain geometries.

37. BUAA Academic Dissertation for Doctoral
3
Diagram 3 Solid propellant rocket grain geometries and corresponding thrust profiles
1.1.1.2 Liquid Propellant
Liquid propellant rockets use two different types of propellant: mono and
bipropellant. Monopropellant rockets use a catalytic bed to decompose the
propellant as illustrated in Diagram 4. This decomposition process is exothermic
and raises the propellant pressure. These rockets are simpler than bipropellant
rockets because they do not require any special cryogenic system and can easily be
operated. They are primarily used for satellite attitude control.
Diagram 4 monopropellant liquid rocket
Bipropellant liquid rockets generate exothermic reactions when both propellants
enter in contact with one another. No external ignition mechanism is required and
combustion can be easily adjusted or stopped by simply reduction the propellant

38. Chapter 1 Introduction
4
mass flows. Most bipropellants must be stored at cryogenic temperatures which
constrains their use to rocket boosters because of the amount of power required to
operate cryogenic systems. These rockets are the best performing and one of the
most complex types of rocket there is because a rather complex turbo-machinery is
required to operate and cool them. A typical bipropellant rocket engine is
illustrated in Diagram 5.
Diagram 5 bipropellant rocket engine
1.1.2 Electric Propulsion Systems
Electric propulsion systems use plasma instead of hot gas to generate thrust. They
use various ionization and acceleration methods and are generally characterised by
higher specific impulses and power requirements. Some of the most common
types of electric propulsion systems will now be introduced.
1.1.2.1 Electrostatic Ion thrusters
Ion thrusters generate thrust by electrostatically accelerating plasma. This plasma
is generated in a discharge chamber by ionizing neutral gas using different means.
Some of these ionization methods will now be illustrated.
DC discharge ion thrusters use electron currents produced by hollow cathodes to
simultaneously ionize the neutral gas stored inside the discharge chamber and
neutralize the exhaust plume as illustrated in Diagram 6. RF and Microwave ion

39. BUAA Academic Dissertation for Doctoral
5
thrusters respectively ionize neutral gas using radiofrequency and microwave
radiations are illustrated in Diagrams 7 and 8.
Diagram 6 DC discharge Ion Thruster
Diagram 7 RF Ion Thruster

40. Chapter 1 Introduction
6
Diagram 8 Microwave Ion Thruster
1.1.2.2 Arc jet
Arc jets generate thrust by replacing the combustion chamber of a conventional
thermal rocket with an electric arc. The neutral gas trapped between the anode and
cathode of an arc jet is ionized resulting in a high temperature plasma that will
subsequently be expanded in a traditional nozzle to generate thrust as it is
illustrated by Diagram 9.
Diagram 9 Arc jet
1.1.2.3 Hall Thruster
Hall thrusters are similar to DC Discharge Ion thrusters in the fact that they use a
hollow cathode to simultaneously ionize the neutral and neutralize the exhaust

41. BUAA Academic Dissertation for Doctoral
7
plume. However their extraction process is somewhat different. They use Lorentz
forces to generate higher thrust levels by simultaneously generating a magnetic
and electric field as illustrated in Diagram 10.
Diagram 10 Hall Thruster
1.1.2.4 Magneto Plasma Dynamic (MPD) Rocket
Magneto plasma dynamic (MPD) rockets ionize neutral gas using an arc discharge
similarly to the one of arc jets but their thrust generation process is somewhat
different to them yet similar to the one of Hall thrusters, i.e.: Lorentz forces.
MPDs use applied and can even under certain circumstance generate a self applied
magnetic field that accelerates plasma particles out of the discharge chamber as it
is illustrated in Diagram 11.

42. Chapter 1 Introduction
8
Diagram 11 Magneto Plasma Dynamic rocket (MPD)
1.1.2.5 Variable Specific Impulse Magneto Plasma Rocket (VASIMR)
A variable specific impulse magneto plasma rocket (VASIMR) is a type of MPD
which can much more precisely control its specific impulse by modified its plasma
exhaust velocity. This enables VASIMRs to switch between a cruise high specific
impulse flight mode and a low specific impulse high thrust manoeuvre flight mode.
Two major components play the role of plasma generator and accelerator. These
are respectively called the Helicon and Ion Cyclotron Radio Frequency Antenna.
VASIMRs don’t have moving nor eroding parts which greatly extend their
operating life and use superconducting electromagnets to confine plasma as
illustrated in Diagram 12.

43. BUAA Academic Dissertation for Doctoral
9
Diagram 12 Variable Specific Impulse Magneto Plasma Dynamic rocket (VASIMR)
1.1.3 Nuclear Propulsion Systems
Nuclear space propulsion systems use nuclear fuel to heat up propellant. The
combustion chamber of conventional rockets is replaced by a nuclear heating
chamber where the temperature of the propellant is increased by direct contact
with the hot nuclear fuel. There are several types of nuclear space propulsion
systems, i.e.: solid, gaseous and radioisotope cores, and their specificities will now
be explained.
1.1.3.1 Solid Core Nuclear Thermal Rocket
The development of nuclear space propulsion systems started in the 1960’s with
the NERVA project. A solid core nuclear rocket as illustrated in Diagram 13 is
composed of a heating chamber where solid nuclear rods are placed and a
traditional nozzle. The propellant is heated up through conductive heat transfer
with the fuel rod’s surface that is at a temperature exceeding .
Appropriate radiation confinement and reaction controllers are put in place in
order to stop nuclear chain reactions.

44. Chapter 1 Introduction
10
Diagram 13 solid core nuclear reactor
1.1.3.2 Gaseous Core Nuclear Thermal Rocket
Gaseous core propulsion systems achieve much higher specific impulses than solid
core nuclear rockets because the hottest regions that usually limit the maximum
achievable temperatures are located far from the core region. The core as
illustrated in Diagram 14 is in a gaseous or plasma state and the propellant
acquires high temperatures by acting as the exhaust coolant of the reactor. The
propellant is heated by the gas core through thermal radiations emitted by the
fission gas that is at a temperature exceeding .
Diagram 14 gas core nuclear reactor

45. BUAA Academic Dissertation for Doctoral
11
1.1.3.3 Radioisotope Thermal Rocket
Radioisotope thermal rockets, i.e.: Poodle’s thrusters, illustrated in Diagram 15
operate following the same principle as solid core nuclear rocket at the exception
that no controller is required to prevent the escalation of the nuclear chain reaction
since radioisotope decay is through stable process. The maximal temperature
achievable by this type of nuclear thermal rocket can reach .
Diagram 15: radioisotope thermal rocket (Poodle thruster)
1.1.4 Performance Comparison
As previously seen there are many types of space propulsion system and each one
of them has its own advantages and drawbacks. A comparative table given below
in table 1 outlines the input power, thrust levels and specific impulses achievable
by each type of space propulsion systems.

46. Chapter 1 Introduction
12
Table 1 Performance characteristics of different space propulsion systems
Input Power
[
Isp [s]
Solid Rocket[1] - 300
Monopropellant Rocket[1] -
Bipropellant Rocket[1] -
Electrostatic Ion thruster [2] 0.4 - 25
Arcjet[3] 1 - 1000
Hall Thruster[2] 1.5 – 4.5
MPD[3] 1 - 1000
VASIMR[4] 200
Solid Core Nuclear Thermal Rocket[5] -
Gaseous Core Nuclear Thermal Rocket[6] -
Radioisotope (Poodle’s) Thermal Rocket[7] -
1.2 ResearchObjective
Since the end of the cold war and the birth of the aerospace industry, space has
been the most important focus and the unreachable limit of researchers all around
the world. Mankind’s ability to project itself higher, faster and deeper into space is
arguably the main cause of its greatest technical, technological and scientific
achievements. However these achievements would have been impossible if
appropriate and sophisticated propulsions systems had not been developed.
Chemical propulsion systems are used to launch spacecraft into orbit and electric
propulsion systems are used to maintain them in orbit or to fare through space.
Chemical propulsion systems burn out, within minutes, most of their fuel in order
to achieve stable orbits around the earth while electric propulsion systems can
operate for months before running out of fuel. However, these last propulsion
systems must completely rely on solar energy or onboard nuclear power sources to
continuously operate for such long periods of time. These energy sources are
limited by the size of solar panels or weight of nuclear power plants which is the
reason why energy has become one of the main limiting factors in the design of
space missions. Technical innovations which led to more energy efficient
spacecraft have so far enabled the objectives of space missions to steadily grow
more ambitious hence more energy demanding but such improvements in energy

47. BUAA Academic Dissertation for Doctoral
13
efficiency have their limits and their growth cannot be indefinitely sustained. A
new approach towards this energetic problem was therefore required and will now
be introduced.
1.2.1 Problematic
As previously explained energy is key in solving the space propulsion question
and the traditional approach used to tackle this energetic problem has always been
to try to achieve greater energy efficiency through optimization or innovation and
the field of ion thrusters does not make exception to that rule. The different
systems of ion thrusters have each been optimized or improved through innovation
in order to increase their performance and energetic efficiency.
Regarding hollow cathodes, it was found that optimizing the length of hollow
cathode influenced the level of energy absorption [8] and that achieving a plasma
density of the order of was required to generate intense electron beams
[9]. Hollow cathodes with large length-to-radius ratio were also found to be harder
to ignite hence would require more energy. [10]
Regarding discharge chambers, it was found that increasing the magnetic strength
of the first closed magnetic contour line of a discharge chamber reduced
Maxwellian electron diffusion and subsequent loss to the anode wall and that it
also better electrostatically confined the ion population. Increasing the strength
and minimizing the area of the magnetic cusps was also found to improve primary
electron confinement and to increase the probability of an ionization collision prior
to loss at the cusp. These modifications effectively reduced the amount of energy
required to ionize a single ion of neutral gas. [11]
Regarding the ion optics, charge exchange ions were understood to play an
important role in the acceleration grids erosion due to sputtering. [12] This erosion
process greatly reduces the system’s operating life by making it less efficiency at
converting electrical energy into ion kinetic energy.
Regarding exhaust plume, the use of ion-ion recombination process in the exhaust
plume neutralization was finally found to be rather effective because this particular

48. Chapter 1 Introduction
14
process takes place faster than the traditional ion-electron recombination process.
Its application could extend thrusters’ lifetime by reducing plume induced damage
and drag [13] and this reduction could maintain the overall energetic requirements
of thrusters that would otherwise have been increased because of thrusters’
reduced performances.
1.2.2 A New Approach: The Self-Sufficiency Principle
The traditional approach taken towards reducing the energy consumption of space
propulsion systems is not the only way. Another approach to tackle this problem
can be found in the Self-Sufficiency Principle.
It states that:”A self-sufficient subsystem is one that does not require others to
fulfil its purpose within its system.” Self-sufficient subsystems are very useful
because they do not require any power inputs and can even output power into their
system. A subsystem can become self-sufficient in two different ways. It can
either naturally fulfil its role hence does not require any power input from its
system or can through internal means produce enough power to support its own
operation.
Applying this approach to all the subsystems of an ion thruster would effectively
cancel the energetic requirements of those subsystems by not using any energy
while still achieving the same results. Let us now consider the electrical efficiency
equation of ion thrusters [2] given below:
(1.1)
Where is the beam power, is the total power input, is the beam current,
is the beam voltage, are other power inputs into the thrusters required to
create the thrusters beam, is the discharge power, is the power associated
with the cathode keeper, is the power associated with the neutralizer keeper
and is the power associated with the acceleration grid. It can be shown that

49. BUAA Academic Dissertation for Doctoral
15
reducing in the denominator would increase the electrical efficiency of an ion
thruster. However for a given , the other power inputs have to be reduced in
order to improve the electrical efficiency. Such improvement could also be
achieved by cancelling any of the components included in these other power
inputs, i.e.: , , . Since the power requirements of all subsystems
cannot be cancelled out and the Self-Sufficiency Principle will still need to be
applied alongside the traditional system optimization approach. The Self-
Sufficiency Principle therefore complements the traditional system optimization
approach and does not fully replace it.
It was already applied on ion thrusters by using permanent magnets to confine the
plasma located inside the discharge chamber instead of using solenoids because
they require additional electrical power to accomplish the same task. This
statement may seem trivial and using permanent magnets to confine discharge
chamber plasma evident however the investigation initiated by this present
research work aims to demonstrate the contrary. It is true that materials possessing
negative electrical polarity levels equal those of ion thruster ion optics do not exist
in nature and have yet to be developed. However naturally-occurring and even
manmade non-electrically powered electron sources do indeed exist.
Radioisotopes are such materials. These elements can naturally emit ionizing
particles or radiation in the form of alpha, beta and gamma decays. Alpha decay
occurs when an alpha particle, i.e.: a helium nucleus, is spontaneously emitted.
Beta decay occurs when an electron or positron is emitted along with a type of
neutrino. The third type of decay, gamma decay, occurs when an instable electron
jumps from a higher to a lower energy state. During this “jump”, an electron will
emit a photon which is what gamma decays effectively are, electromagnetic
radiations. These decay both results in the transmutation of one emitting element,
i.e.: the mother nuclide, into a resulting element, i.e.: the daughter nuclide, or into
a stable element of the periodic table.
Radioisotopes emitting particles could be used as viable alternative electron
sources that could replace traditional hollow cathodes in the plasma generation

50. Chapter 1 Introduction
16
process of ion thrusters. This would just like in the case of discharge chambers
using permanent magnets for plasma containment, require no additional electrical
energetic input hence the title of this doctoral thesis, Feasibility study of
radioisotope based electron sources for space applications.
1.2.3 Literature Survey
Nuclear materials and radioisotopes have been used for a long time in space
applications and propulsion systems. Nuclear energy was envisioned to power
high thrust and high specific impulse rockets that could enable fast interplanetary
space travels but safety concerns have so far stalled their deployment in space.
[14] However, radioisotopes have already been deployed since the 1960’s in space
and earth applications. They were used as heat sources in Radioisotope Heater
Units (RHU) to provide heat from a radioactive decay for electronics and other
equipment in the cold of space, in Radioisotope Thermoelectric Generators (RTG)
to convert thermal energy from radioactive decay into electrical power for polar
bases, satellites or unmanned space probes [14], in radioisotope thermionic
converters to transform thermionic electron currents into electricity [15] and also
in thermal rockets as well in which exhaust gas was heated by direct contact with a
radioisotope heat source [16].
A concept linking the use of RTGs and Electric Space Propulsion systems, i.e.:
Radioisotope Electric Propulsion (REP) systems, has also been developed and
deployed in space. [14, 17-20].
However, no similar use of radioisotopes as electron sources for space applications
has ever been expressed nor investigated although some research fields came very
close to this present research direction:, i.e.: Hollow cathodes were once
considered as potential micro-thrusters [21], radioactive fragments were inserted
into a magneto hydrodynamic (MHD) generator to increase gas ionization [22];
the alpha particles of Curium-244 were used for direct micro and nano-newton
thrust generation [23].
The fact remains that the use of decay radioisotope based plasma generators
is an unexplored and innovative research field that was initiated by the application

51. BUAA Academic Dissertation for Doctoral
17
of the Self-Sufficiency Approach. It is hoped that the effectiveness of this rather
unconventional method to tackle the problem of energetic deficiency in the space
environment will be demonstrated in this thesis. The objectives of this research
work are to first determine whether radioisotopes can replace hollow cathodes as
primary electron sources in DC ion thrusters, then to outline the engineering
requirements that would render this technology viable and finally to maximize the
use of all of the properties of radioisotopes. The background knowledge required
to apply all the elements of this technology will first introduced in Chapter 2, then
the development of the first decay radioisotope electron source and its
application will be explained in Chapter 3, the first radioisotope heated hollow
cathode and thermionic plasma rocket engine will be introduced in Chapter 4
before finally concluding with some insight on the work which lies ahead of this
initial feasibility study.

52. 18

53. BUAA Academic Dissertation for Doctoral
19
2 Background
2.1 PowerGeneration
RTGs are devices that can convert heat into electricity. There are different types of
RTG and each one of them has its own operating mode and range of electric
conversion efficiencies. Static RTGs are the simplest of all RTGs. they convert
heat into electricity using the Seebeck effect which is a typical example of
electromotive forces whereby metal plates react to a temperature gradient between
them by exchanging electron see Diagram 16.
.
Diagram 16 Radioisotope Thermoelectric Generator using the Seebeck Effect
These RTGs can reach a maximal electric conversion efficiency of 10%. Dynamic
RTGs operate following thermodynamic cycles such as the Brayton or Stirling
cycles. Gas located between the hot and cold junctions drives a piston which
motion is converted into electricity. They are the most efficient type of RTG and
can reach electric conversion efficiencies as high as 30%. Other types of RTG are
still at an early stage of development. Thermophotovoltaic RTGs for instance
operate by converting infrared photons emitted by hot metallic surfaces into
electricity. These RTGs can reach relatively good electric conversion efficiencies
and have demonstrated maximal values of up to 20%[24].

54. Chapter 2 Background
20
Static RTGs will be used in this study because their relative simplicity will keep
them lightweight and compact. Although electric conversion efficiencies of 6.3%
have already been reached [25] a conservative value of 5% will be used instead.
Assuming that the radioisotope specific power is known, the electric power
generated by a RTG can directly be calculated using the following equation:
(2.1)
where is the thermal conversion efficiency, is the radioisotope mass and
is the radioisotope specific heat. Radioisotope specific heats have already
been tabulated [26] but they can also be calculated using the following equation
[24] at the condition that the radioisotope in question is primarily an or
emitter:
⁄ (2.2)
where is the radioisotope decay energy, is the radioisotope decay constant,
is Avogadro’s number and is the atomic weight. The decay constant is
given by:
⁄⁄ (2.3)
where ⁄ is the half life of the radioisotope. Eq. 2.2 only provides the specific
heat generated by the decay of the mother nuclide but it should be used with great
care because some radioisotopes have highly energetic daughter nuclides and
using Eq. 2.2 would result in high inaccuracies. Lead-210, for example, has a
calculated specific heat of but its actual specific heat is times
larger, i.e.: [26], due to the highly energetic decay heat of its daughter
nuclides.

55. BUAA Academic Dissertation for Doctoral
21
2.2 Radiation Shielding Requirement
Some radioisotopes emit radiations when they decay and these radiations, which
can take numerous forms, i.e.: gamma and x-rays, can have a negative impact on
human physiology and can also damage spacecraft instruments as illustrated in
Diagram 17. They must therefore be attenuated down to acceptable levels using an
appropriate shielding.
Diagram 17 Radiation shielding illustration
The shielding thickness required to achieve a given shielded exposure at a certain
distance of a given radioisotope heat source can be calculated using the radiation
shielding equation [27]:
(2.4)
where is the shielded exposure, is the unshielding exposure, is the linear
attenuation coefficient and is the radiation shielding thickness. Assuming a set
shielded exposure, the unshielded exposure of a given radioisotope is given by
[28]:
(2.5)

56. Chapter 2 Background
22
where is the gamma factor, i.e.: the exposure of a given radionuclide from a
distance of 1 meter per unit decay, and is the equivalent activity, i.e.: the
decay rate equivalent to a certain quantity of radioisotope generating a specific
amount of thermal power. Values of the gamma factor for different radioisotopes
are readily available in the literature[29]. The equivalent activity is itself given by:
(2.6)
where is the specific activity of a radioisotope and is the equivalent
radioisotope mass, i.e.: the radioisotope mass required to generate a given amount
of thermal power. The specific activity of a radioisotope is given by:
⁄ (2.7)
and the equivalent radioisotope mass is given by:
⁄ (2.8)
where is the target thermal power that the radioisotope is supposed to
generate. The linear attenuation coefficient introduced in Eq. 2.4 is given by[27]:
(2.9)
where is the mass attenuation coefficient and is the density of the shielding
material. The mass attenuation coefficient varies as a function of the irradiation,
i.e.: X or gamma rays, energy and the selected shielding material. Values of mass

57. BUAA Academic Dissertation for Doctoral
23
attenuation coefficients are readily available in the literature[30, 31]. Solving Eq.
2.4 finally yields the radiation shielding thickness required to achieve a given
shielded exposure at a certain distance of a radioisotope heat source of a given
thermal power:
⁄ ⁄ (2.10)

59. BUAA Academic Dissertation for Doctoral
25
3 decay radioisotope electron source
The development of a decay radioisotope electron source will now be outlined
then its applications will be explained.
3.1 RadioisotopeSpecific Activity
Neutral gas ionization is an important process of ion thrusters’ operation and
before decay radioisotope electrons may be used to fulfil this task their velocity
and current density must first be calculated. These two parameters will then later
be used to calculate the degree of ionization achieved by a given radioisotope. The
activity density of a radioisotope will be described here as the number of decays
that a radioisotope can achieve per second and per unit volume and will be
expressed as:
(3.1)
where is the number density of radioisotope atoms which is given by:
⁄ (3.2)
Where is the radioisotope density.
3.2 ElectronCurrent Density
In order to calculate radioisotope electron current densities, it is useful to first
consider a radioisotope source in the form of a cubic volume of unit dimensions
completely filled with radioisotope atoms as illustrated in Diagram 18. Assuming
that a radioisotope decays isotropically, its activity density in any given direction
will be equal to the sixth of its activity density:

60. Chapter 3 decay radioisotope electron source
26
⁄ (3.3)
Diagram 18 cubic volume of unit dimensions completely filled with radioisotope atoms
Multiplying the activity in a single direction obtained in Eq. 3.3 by the electron
charge gives the radioisotope current density emitted from a single direction that is
illustrated in Diagram 19:
(3.4)
where is the electron charge.
1cm
1cm
1cm

61. BUAA Academic Dissertation for Doctoral
27
Diagram 19 radioisotope electron current emitted from one side of a cubic volume of
unit dimensions
3.3 ElectronVelocity.
Beta minus radioisotope electrons were assumed to convert most of their decay
energy into kinetic energy because of their extremely small inertia:
⁄ (3.5)
where is the electron particle’s mass and is its velocity. Rearranging Eq. 3.5
gives the particle velocity:
√ ⁄ (3.6)
The radioisotope decay energy may not be directly substituted to the kinetic
energy and must first be altered in order to account for the electron Maxwellian
energy distribution. A mean decay energy equivalent to a third of the radioisotope
decay energy must be used in order to calculate the velocity of decay
radioisotope electrons[32]:
⁄ (3.7)
where is the mean decay energy. Eq. 3.6 gives the velocity of particles
travelling at non relativistic velocities however many decay radioisotope
electrons travel at relativistic velocities due to their high decay energies and low
inertias. A new expression is required to calculate the velocity of electrons
travelling seemingly faster than the speed of light and the relativistic kinetic
energy equation can be used to this end. It is given by:

62. Chapter 3 decay radioisotope electron source
28
(3.8)
where is the Lorentz factor and is the speed of light. The Lorentz factor is
itself given by:
√ ⁄⁄ (3.9)
Combining Eqs. 3.8 and 3.9 then solving for the velocity, yields the relativistic
electron velocity:
√ ⁄⁄ (3.10)
Eq. 3.10 should be used when Eq. 3.6 returns a value greater than the speed of
light in order to obtain physically sound results.
3.4 Gas Ionization
Removing one electron from each neutral atom of a gas results in a plasma
composed of negatively charged free electrons and positively ions. The process
through which neutral atoms loss electrons is called ionization and recombination
is the inverse process through which ions gain electrons as illustrated in Diagram
20.

63. BUAA Academic Dissertation for Doctoral
29
Diagram 20 Ionization and recombination processes
Neutral gas ionization can be achieved using many different ways but electron
impact ionization is the one used in conventional DC discharge ion thrusters.
During this process, an electron current of a given energy is fired at neutral atoms
and ionizes them through collision. The resulting plasma is therefore composed of
one ion and two lose electrons for each neutral atom as illustrated in Diagram 21.
Diagram 21 electron release during ionization process
The total number of ions produced by an electron discharge in particles per second
is given by:

64. Chapter 3 decay radioisotope electron source
30
〈 〉 〈 〉 (3.11)
Where is the neutral atom density, is the primary, i.e.: radioisotope, electron
density, is the ionization cross section, is the primary electron velocity, is
the discharge volume, is the plasma electron density and is the plasma
electron velocity. The terms between brackets are called the reaction rate
coefficient, i.e.: the ionization cross section averaged over the distribution of
electron energies. Assuming that the ionization process is dominated by primary
electrons and considering that all primary electrons have the same mean decay
energy hence velocity Eq. 3.11 becomes:
(3.12)
for the equivalent ion current produced by a discharge of radioisotope electrons.
Eq. 3.11 was developed with the assumption of ionization equilibrium, i.e.: that all
plasma particles are evenly distributed throughout the volume. This can be
understood as follows: Eq. 3.12 gives the ion and secondary electron current
produced within a unit volume by a given primary electron current density that is
subsequently multiplied by the discharge chamber’s volume in order to account for
the total ion current generated hence the ionization equilibrium assumption.
Keeping this in mind the primary electron current density colliding with a unit
volume of neutral atoms can be extracted from Eq. 3.12 and is equal to:
(3.13)
Eq. 3.13 may now be rewritten as:
(3.14)

65. BUAA Academic Dissertation for Doctoral
31
The primary electron current density given by Eq. 3.13 must be equated to the
averaged radioisotope electron current density that will collide with the neutral
atoms of a discharge chamber. This averaged radioisotope electron current density
can be obtained by dividing the total radioisotope electron current with the
discharge chamber’s volume:
⁄ (3.15)
Where is a unit volume, is the total radioisotope current and is a unit
surface area. A unit volume and surface area were also added to Eq. 3.15 in order
to balance its units. The total radioisotope current is equal to the sum of all
radioisotope currents emitted from the ionizing sides of the discharge chamber and
is given by:
(3.16)
where is the number of sides involved in the ionization process and is the
surface area of one of the sides of the ionization chamber. has a maximum
value of 4 since two sides are required for the neutral atom injection and plasma
extraction process as illustrated in Diagram 22. Assuming that the discharge
chamber is a cube of length, , the averaged radioisotope electron current density
can now be expressed as:
⁄ (3.17)

66. Chapter 3 decay radioisotope electron source
32
Diagram 22 Discharge chamber filled with neutral gas being ionized from its 4 sides by
radioisotope electron currents and neutral atoms and plasma being extracted from two
of its sides
Where is the discharge chamber length. Replacing the primary electron current
density of Eq. 3.14 by the averaged radioisotope electron current obtained in Eq.
3.17 yields a new expression for the equivalent ion current produced by a
discharge of radioisotope electrons:
⁄ (3.18)
Eq. 3.18 becomes:
⁄ (3.19)
for the density of the ions current production rate, i.e.: the number of secondary
electrons produced per unit volume. Let us note that Eq. 3.19 takes this new multi
directional ionization pattern and the discharge chamber geometry into
consideration. Assuming that the ion production and loss rates are equal, the
degree of ionization of the neutral gas can finally be found:

67. BUAA Academic Dissertation for Doctoral
33
⁄ ⁄ (3.20)
It should also be noted that based on Eq. 3.20 the degree of ionization of a neutral
gas volume solely depends on the ionization pattern, radioisotope and geometric
parameters, i.e.: the number of sides exposed to radioisotope electron currents, the
activity of the radioisotope used to ionize the neutral gas, the ionization cross
section and the discharge chamber geometry, but not on gas properties such as the
density or temperature. This is not accurate and it will later be shown that the
achievable degree ionization will be influenced by plasma effects such as
recombination and thermalization that would however prevent the generation of a
sustainable plasma.
The degree of ionization could potentially the 100% as the discharge chamber
length goes to 0 because Eq. 3.20 which describes the degree of ionization is not
applicable for infinitesimally small values of discharge chamber length. The
degree of ionization of a plasma is usually given by: , Where is the
ion density and is the neutral particle density. Obtaining the degree of
ionization using this fundamental equation can only be achieved iteratively
because all previous values of ion densities must be used to obtain new values of
ion and neutral densities. However if the plasma a cold plasma is assumed, just
like in traditional discharge chambers, then the neutral density will always remain
much larger than the ion density, i.e.: , and the fundamental equation can
be simplified into : . This assumption was used in Eq. 3.20, i.e.:
, however this expression of the degree of ionization is inversely proportional
to the discharge chamber length, i.e.: and it will always go to infinity as the
discharge chamber length tends to zero, i.e.: . Hence the value of
degree of ionization exceeding 100% as the discharge chamber length gets closer
to 0.

68. Chapter 3 decay radioisotope electron source
34
3.5 ElectronVelocity Modulation
The degree of ionization can be optimized by maximizing Eq. 3.20 and this can
only be achieved by maximizing the electron ionization cross section since the
maximal number of ionizing sides and radioisotope activity per side are fixed for a
given geometric configuration and radioisotope.
The electron ionization cross section of xenon illustrated in Diagram 23 [33] is a
function of the incident electron energy and the maximal ionization cross section
appear to occur at a relatively low electron energy, i.e.: 30 , which is
equivalent to a velocity of ⁄ . However the energy of most
decay radioisotope electrons is of the order of several kilo and even
megaelectronvolts and they must therefore be decelerated in order to maximize the
electron ionization cross section and consequently the ionization potential of
radioisotopes.
Diagram 23 Electron ionization cross section of Xenon (5p orbit)
Electrons are subatomic particles that can only be influenced by gravitational,
magnetic and electric fields but only the latter ones can practically be used to
modulate electrons’ velocities without altering their trajectories.

69. BUAA Academic Dissertation for Doctoral
35
The velocity modulation of an electron crossing an electrostatic field is illustrated
in Diagram 24. Electrostatic forces are represented by vectors going from the
positive to the negative polarity. An electron travelling in the direction opposite to
the one of electrostatic forces will be accelerated as in (a) while one that travels in
the same direction just like in (b) will be decelerated. Electrons gain energy from
electrostatic fields when they are accelerated and lose energy when they are
decelerated. Both processes however always consume energy and never generate
any.
Diagram 24 Electron velocity modulation using an electrostatic field
The power required by an Electron Velocity Modulator (EVM) is given by the
difference of kinetic energy between both states:
( )⁄ (3.21)
Where is an electron’s final kinetic energy, is its initial kinetic energy,
is its final velocity and its initial velocity. The electron velocities can be
obtained using Eqs. 3.6 or 3.10. The following expression is however more
appropriate because it gives the power required to modulate an electron stream
instead of a single particle:

70. Chapter 3 decay radioisotope electron source
36
̇ (3.22)
where ̇ is the electron flow rate. An electron current is defined as the sum of all
charged particles crossing a given surface area per second:
̇ = (3.23)
Combining Eqs 3.4, 3.21, 3.22 and 3.23 yields a new expression for Eq. 3.23:
( )⁄ (3.24)
Electric power can also be expressed as:
(3.25)
where is the voltage. Rearranging Eq. 3.25 and combining it with Eq. 3.24
finally yields the voltage required to modulate the electron velocities:
( )⁄ (3.26)
3.6 Gas BreakdownVoltage
A gas trapped between two electrodes across which a high electric potential is
applied will start to demonstrate dielectric properties at a given voltage and

71. BUAA Academic Dissertation for Doctoral
37
generate an electric arc. Electric breakdown can occurs in a gaseous environment
but also in vacuum as illustrated in Diagrams 25 and 26.
Diagram 25 Electric breakdown at atmospheric Pressure
Diagram 26 Vacuum dielectric breakdown
This phenomenon occurs at a breakdown voltage given by Paschen’s Law [34]:
⁄⁄⁄ (3.27)

72. Chapter 3 decay radioisotope electron source
38
Where is the length of the gap that separates both electrodes, is the gas
pressure, , and are three constants specific to the gas being used. Eq. 3.27
can be simplified by introducing a new constant given by:
⁄⁄ (3.28)
and becomes:
⁄ (3.29)
Electric breakdowns must be prevented to extend the operating life of electrodes.
Eq. 3.29 can be used to plot Paschen curves that give the breakdown voltage of
different gases as a function of the product and the Paschen curve of xenon
illustrated in Diagram 27 was plotted using the following values 19.3 and 0.376
for the constants and [34].

73. BUAA Academic Dissertation for Doctoral
39
Diagram 27 Breakdown voltage in xenon as a function of the product (p.d) [34]
It appears that the largest values of breakdown voltage are obtained for extremely
small and large values of the product . This means that gas breakdowns are less
likely to occur in a vacuum and high pressure environment. Small gap distances
and pressures prevent gas breakdown by reducing the quantity of particles
available to initiate an avalanche breakdown whilst large gap distances and
pressures limit gas breakdown by increasing the particle load that must be carried
by a given voltage. It should however be noted that breakdown voltages increase
linearly for large values of and exponentially for smaller ones. Ion thrusters’
discharge chambers are operated at very low pressures, i.e.: , can
safely be approximated by a vacuum. These kinds of pressure will yield extremely
high breakdown voltages because they belong to the lower end of the Paschen’s
curve where the breakdown voltage grows exponentially with reduced pressures.
Vacuum breakdown voltages are given by:

74. Chapter 3 decay radioisotope electron source
40
(3.30)
where is a constant that depends on the electrode’s material and is usually of the
order of ⁄ [35]. Neutral gas electric breakdowns will therefore be rather
unlikely since gap could easily sustain a potential of several hundreds of
volts.
3.7 PowerGeneration
The use of radioisotopes as electron sources in this plasma generator could prove
to be more energy efficient than traditional ion thrusters’ and their properties could
further be exploited through the application of the Self-Sufficiency Principle. This
present beta minus decay radioisotope plasma generator could achieve a state of
self-sufficiency by powering its EVM using the decay heat of its radioisotope
electron source which can only be achieved using a RTG. The radioisotope mass
required by Eq. 2.1 is given in this case by:
(3.31)
where is the radioisotope volume that is given by:
(3.32)
Where is the thickness of the radioisotope electron source that is taken here as
unity.

75. BUAA Academic Dissertation for Doctoral
41
3.8 Application: Ion thruster
This decay radioisotope electron source can be used to generate plasma.
Plasma generators have numerous applications and could be used as a plasma
source for most space propulsion systems. Ion thrusters were selected as the first
application of this new technology and the results achieved through its use will
now be displayed and discussed.
3.8.1 Calculations
Once plasma has been generated, ions must be extracted in order to produce a
useful thrust. This can be accomplished by establishing an electrostatic field
between the anode wall and an acceleration grid. This potential difference, equal
to the beam voltage, will draw ions out of the discharge chamber through the
apertures of the acceleration grid in order to generate a beam current that will
create the thrust that propels the spacecraft. The thrust generated by a DC
discharge ion thruster is given by:
√ ⁄ (3.33)
where is the propellant atomic mass. The maximum beam voltage depends on
the breakdown voltage of the gas and acceleration grid material. As seen earlier
the neutral gas is not likely to breakdown because of its low vacuum pressure.
Acceleration grids are often made out of molybdenum which has a voltage
breakdown ranging between and ⁄ . This gives a maximal beam
voltage of to for a thick acceleration grid. A beam voltage of
will however be used because such voltage was found to yield good
performances [36]. The beam current is given by:
⁄ (3.34)

76. Chapter 3 decay radioisotope electron source
42
where is the ion density, is the acoustic velocity, is the grid surface area
and is the grid transparency. The ion density depends on the degree of
ionization obtained in Eq. 3.20 and is given by:
(3.35)
The neutral density could take any value however larger values will prevent stable
plasma to be sustained because they increase the rate of recombination. Typical
values of the order of were found to enable stable discharge chamber
plasma[37]. The acoustic velocity is given by:
√ ⁄ (3.36)
where is the Boltzmann’s constant, is the electron temperature and is the
ion mass. Electrons typically have a temperature of inside discharge
chambers[37] which gives a typical acoustic velocity of ⁄ for discharge
chamber xenon ions. The grid surface area is given by:
(3.37)
A typical value of 0.8 will be used for the grid transparency [2]. The beam power,
i.e.: the power required to extract ions, is given by:
(3.38)

77. BUAA Academic Dissertation for Doctoral
43
The thruster must also power its ion extraction process in order to become a self-
sufficient subsystem and the power remaining after the deceleration of
radioisotope electrons must be used to this end. This remaining power is equal to:
(3.39)
If the remaining power is greater than the beam power, i.e.: , then the
excess energy can be used to power the spacecraft however if the remaining power
is lower than the beam power, i.e.: , the beam voltage will then need to be
reduced so that the product of Eq. 3.38 may equal the remaining power, i.e.:
⁄ .

78. Chapter 3 decay radioisotope electron source
44
3.8.2 Results
The performance characteristics obtained using different radioisotopes will now be
presented. 16 beta minus radioisotopes, i.e.: , , , ,
, , , , , , , , , ,
and , were selected for this device because of their relatively long
half lives and low decay energies. Long half lives enable their use in typical space
missions and low decay energies minimize the required EVM voltage. These
radioisotopes were separated into three performance groups according to their
maximal degree of ionization. , , , and belong to the
first performance group, , , , , and to the
second and , , , and to the third one. Relevant
radioisotope characteristics are listed in table 2 and their performance
characteristics are illustrated in Diagrams 28 to 91. Diagrams 28 to 43 illustrate
the degree of ionization and thrust level achieved by the - decay radioisotope
electron source thruster application using different radioisotopes. The degree of
ionization and thrust level were obtained using Eqs. 3.20 and 3.33 for different
values of number of ionizing sides and discharge chamber length. Diagrams 44 to
59 illustrate the thrust density achieved by the - decay radioisotope electron
source thruster application, with 4 ionizing sides and at different RTG electric
conversion efficiencies, using different radioisotopes. The thrust density is
equivalent to the ratio of the thrust level generated by the thruster over its surface
area for a given discharge chamber length. The thruster surface area was
calculated according to the design of the radioisotope propulsive cell illustrated in
diagram 93 and can easily be found to be equal to .
Diagrams 60 to 75 illustrate the radioisotope mass and the generated excess power
densities of the - decay radioisotope electron source thruster application using
different radioisotopes. The radioisotope mass and generated excess power
densities are equivalent to the ratios of the radioisotope mass and generated excess
power over the thruster surface area. The radioisotope mass was calculated using
the radioisotope density and volume which was derived from diagram 93 and can

79. BUAA Academic Dissertation for Doctoral
45
easily be found to be equal to ( ). The generated excess
power was obtained by subtracting the beam power given in Eq. 3.38 from the
remaining power given in Eq. 3.39, i.e.: when the remain power
exceeded the beam power. A Beam voltage of equivalent to the one used
on the NSTAR thruster[50] was used to derive these results. Diagram 76 illustrates
the minimal electric conversion efficiency required to operate the - decay
radioisotope electron source thruster application with a discharge length of
using different radioisotopes. These values were obtained by first equating the
beam and remain powers respectively obtained in Eqs. 3.38 and 3.39 and by then
solving for the electric conversion efficiency calculated from Eq. 2.1, i.e.:
. All thrust, radioisotope mass and generated excess power densities
previously obtained were ultimately compiled in diagrams 77 to 85. Radioisotopes
were arranged into 3 categories depending on their thrust density performances.
Additional metrics called the specific thrust and excess power were finally
introduced in diagrams 86 to 91. The specific thrust and excess power are
equivalent to the thrust level and generated excess power achieved per kilogram of
radioisotope material. These metrics were obtained by simply dividing the values
of thrust and excess power densities obtained by the ones of radioisotope mass
density. These results were also arranged into the previous 3 performance
categories.

80. Chapter 3 decay radioisotope electron source
46
3.8.2.1.1.1.1.1
3.8.2.1.1.1.1.2 Table 2 Radioisotope Data
Characteristics
atomic number
Decay Energy
half-life
density
mass attenuation coefficient [38]
Gamma Ray Dose Constant
[29]
Radioisotope Specific Heat [26] *
*calculated values
3.8.2.1.1.1.1.3
3.8.2.1.1.1.1.4 Table 2 Radioisotope Data (continued)
Characteristics
atomic number
Decay Energy
half-life
density
mass attenuation coefficient [39]
Gamma Ray Dose Constant
[29]
Radioisotope Specific Heat [26]
*calculated values

81. BUAA Academic Dissertation for Doctoral
47
3.8.2.1.1.1.1.5
3.8.2.1.1.1.1.6 Table 2 Radioisotope Data (continued)
Characteristics
atomic number
Decay Energy
half-life
density
mass attenuation coefficient [38]
Gamma Ray Dose Constant [29]
Radioisotope Specific Heat [26] *
*calculated values
3.8.2.1.1.1.1.7
3.8.2.1.1.1.1.8 Table 2 Radioisotope Data (continued)
Characteristics
atomic number
Decay Energy
half-life
density
mass attenuation coefficient [38]
Gamma Ray Dose Constant [29]
Radioisotope Specific Heat [26] * * *
*calculated values

83. BUAA Academic Dissertation for Doctoral
47
Diagram 28 Thrust and degree of ionization achieved by for different numbers of
ionizing sides as a function of the discharge chamber length
Diagram 29 Thrust and degree of ionization achieved by for different numbers of
ionizing sides as a function of the discharge chamber length

84. Chapter 3 decay radioisotope electron source
48
Diagram 30 Thrust and degree of ionization achieved by for different numbers
of ionizing sides as a function of the discharge chamber length
Diagram 31 Thrust and degree of ionization achieved by for different numbers of
ionizing sides as a function of the discharge chamber length

85. BUAA Academic Dissertation for Doctoral
49
Diagram 32 Thrust and degree of ionization achieved by for different numbers of
ionizing sides as a function of the discharge chamber length
Diagram 33 Thrust and degree of ionization achieved by for different numbers of
ionizing sides as a function of the discharge chamber length

86. Chapter 3 decay radioisotope electron source
50
Diagram 34 Thrust and degree of ionization achieved by for different numbers of
ionizing sides as a function of the discharge chamber length
Diagram 35 Thrust and degree of ionization achieved by for different numbers of
ionizing sides as a function of the discharge chamber length

87. BUAA Academic Dissertation for Doctoral
51
Diagram 36 Thrust and degree of ionization achieved by for different numbers of
ionizing sides as a function of the discharge chamber length
Diagram 37 Thrust and degree of ionization achieved by for different numbers of
ionizing sides as a function of the discharge chamber length

88. Chapter 3 decay radioisotope electron source
52
Diagram 38 Thrust and degree of ionization achieved by for different numbers of
ionizing sides as a function of the discharge chamber length
Diagram 39 Thrust and degree of ionization achieved by for different numbers of
ionizing sides as a function of the discharge chamber length

89. BUAA Academic Dissertation for Doctoral
53
Diagram 40 Thrust and degree of ionization achieved by for different numbers
of ionizing sides as a function of the discharge chamber length
Diagram 41 Thrust and degree of ionization achieved by for different numbers of
ionizing sides as a function of the discharge chamber length

90. Chapter 3 decay radioisotope electron source
54
Diagram 42 Thrust and degree of ionization achieved by for different numbers of
ionizing sides as a function of the discharge chamber length
Diagram 43 Thrust and degree of ionization achieved by for different numbers
of ionizing sides as a function of the discharge chamber length

91. BUAA Academic Dissertation for Doctoral
55
Diagram 44 Thrust density achieved by for different electric conversion efficiencies
as a function of the discharge chamber length
Diagram 45 Thrust density achieved by for different electric conversion
efficiencies as a function of the discharge chamber length

92. Chapter 3 decay radioisotope electron source
56
Diagram 46 Thrust density achieved by for different electric conversion
efficiencies as a function of the discharge chamber length
Diagram 47 Thrust density achieved by for different electric conversion efficiencies
as a function of the discharge chamber length

93. BUAA Academic Dissertation for Doctoral
57
Diagram 48 Thrust density achieved by for different electric conversion
efficiencies as a function of the discharge chamber length
Diagram 49 Thrust density achieved by for different electric conversion
efficiencies as a function of the discharge chamber length

94. Chapter 3 decay radioisotope electron source
58
Diagram 50 Thrust density achieved by for different electric conversion
efficiencies as a function of the discharge chamber length
Diagram 51 Thrust density achieved by for different electric conversion
efficiencies as a function of the discharge chamber length

95. BUAA Academic Dissertation for Doctoral
59
Diagram 52 Thrust density achieved by for different electric conversion
efficiencies as a function of the discharge chamber length
Diagram 53 Thrust density achieved by for different electric conversion
efficiencies as a function of the discharge chamber length

96. Chapter 3 decay radioisotope electron source
60
Diagram 54 Thrust density achieved by for different electric conversion
efficiencies as a function of the discharge chamber length
Diagram 55 Thrust and degree of ionization achieved by for different electric
conversion efficiencies as a function of the discharge chamber length

97. BUAA Academic Dissertation for Doctoral
61
Diagram 56 Thrust density achieved by for different electric conversion
efficiencies as a function of the discharge chamber length
Diagram 57 Thrust density achieved by for different electric conversion
efficiencies as a function of the discharge chamber length

98. Chapter 3 decay radioisotope electron source
62
Diagram 58 Thrust density achieved by for different electric conversion
efficiencies as a function of the discharge chamber length
Diagram 59 Thrust density achieved by for different electric conversion
efficiencies as a function of the discharge chamber length

99. BUAA Academic Dissertation for Doctoral
63
Diagram 60 Radioisotope mass and excess power densities achieved by as a function
of the discharge chamber length
Diagram 61 Radioisotope mass and excess power densities achieved by as a
function of the discharge chamber length

100. Chapter 3 decay radioisotope electron source
64
Diagram 62 Radioisotope mass and excess power densities achieved by as a
function of the discharge chamber length
Diagram 63 Radioisotope mass and excess power densities achieved by as a
function of the discharge chamber length

101. BUAA Academic Dissertation for Doctoral
65
Diagram 64 Radioisotope mass and excess power densities achieved by as a
function of the discharge chamber length
Diagram 65 Radioisotope mass and excess power densities achieved by as a
function of the discharge chamber length

102. Chapter 3 decay radioisotope electron source
66
Diagram 66 Radioisotope mass and excess power densities achieved by as a
function of the discharge chamber length
Diagram 67 Radioisotope mass and excess power densities achieved by as a
function of the discharge chamber length

103. BUAA Academic Dissertation for Doctoral
67
Diagram 68 Radioisotope mass and excess power densities achieved by as a
function of the discharge chamber length
Diagram 69 Radioisotope mass and excess power densities achieved by as a
function of the discharge chamber length

104. Chapter 3 decay radioisotope electron source
68
Diagram 70 Radioisotope mass and excess power densities achieved by as a
function of the discharge chamber length
Diagram 71 Thrust and degree of ionization achieved by as a function of the
discharge chamber length

105. BUAA Academic Dissertation for Doctoral
69
Diagram 72 Radioisotope mass and excess power densities achieved by as a
function of the discharge chamber length
Diagram 73 Radioisotope mass and excess power densities achieved by as a
function of the discharge chamber length

106. Chapter 3 decay radioisotope electron source
70
Diagram 74 Radioisotope mass and excess power densities achieved by as a
function of the discharge chamber length
Diagram 75 Radioisotope mass and excess power densities achieved by as a
function of the discharge chamber length

107. BUAA Academic Dissertation for Doctoral
71
Diagram 76 Minimal electric conversion efficiency of the selected radioisotopes

108. Chapter 3 decay radioisotope electron source
72
Diagram 77 Thrust densities achieved by the radioisotopes of the first performance
group at their minimal electric conversion efficiency as a function of the discharge
chamber length
Diagram 78 Thrust densities achieved by the radioisotopes of the second performance
group at their minimal electric conversion efficiency as a function of the discharge
chamber length

109. BUAA Academic Dissertation for Doctoral
73
Diagram 79 Thrust densities achieved by the radioisotopes of the third performance
group at their minimal electric conversion efficiency as a function of the discharge
chamber length
Diagram 80 Radioisotope mass density achieved by the first performance group at their
minimal electric conversion efficiency as a function of the discharge chamber length

110. Chapter 3 decay radioisotope electron source
74
Diagram 81 Radioisotope mass density achieved by the second performance group at
their minimal electric conversion efficiency as a function of the discharge chamber
length
Diagram 82 Radioisotope mass density achieved by the third performance group at their
minimal electric conversion efficiency as a function of the discharge chamber length

111. BUAA Academic Dissertation for Doctoral
75
Diagram 83 Excess power density achieved by the first performance group at their
minimal electric conversion efficiency as a function of the discharge chamber length
Diagram 84 Excess power density achieved by the second performance group at their
minimal electric conversion efficiency as a function of the discharge chamber length

112. Chapter 3 decay radioisotope electron source
76
Diagram 85 Excess power density achieved by the third performance group at their
minimal electric conversion efficiency as a function of the discharge chamber length
Diagram 86 Specific thrust achieved by the first performance group at their minimal
electric conversion efficiency as a function of the discharge chamber length

113. BUAA Academic Dissertation for Doctoral
77
Diagram 87 Specific thrust achieved by the second performance group at their minimal
electric conversion efficiency as a function of the discharge chamber length
Diagram 88 Specific thrust achieved by the third performance group at their minimal
electric conversion efficiency as a function of the discharge chamber length

114. Chapter 3 decay radioisotope electron source
78
Diagram 89 Specific excess power achieved the first performance group at their minimal
electric conversion efficiency as a function of the discharge chamber length
Diagram 90 Specific excess power achieved the second performance group at their
minimal electric conversion efficiency as a function of the discharge chamber length

115. BUAA Academic Dissertation for Doctoral
79
Diagram 91 Specific excess power achieved the third performance group at their
minimal electric conversion efficiency as a function of the discharge chamber length

116. Chapter 3 decay radioisotope electron source
80
3.8.3 Discussion
3.8.3.1 Novel Type of Ion Thruster
It was demonstrated in this research work that radioisotopes can be used as
electron sources for space applications but beta minus decay radioisotope electrons
must be decelerated prior to the neutral gas ionization because of their high decay
energies. This deceleration process requires additional power that can partly or
total be drawn from the heat generated by radioisotopes.
Such combination of a radioisotope electron source, EVM and RTG is truly
innovative and led to the invention of a totally new type of ion thruster which was
named the “MINAKA” thruster after its inventor’s mother, Micheline Nathalie
Kapinga.
Since the MINAKA thruster was developed following the Self-Sufficiency
Principle its operation had to be guaranteed independently from other subsystems
and external power supply hence the need to use the heat generated by the
radioisotope in order to power the EVM and accelerator grid. Increasing the
quantity of radioisotope in order to fully power the thruster could not be
considered because it would have been similar to creating a RTG instead of a self-
sufficient electron source.
3.8.3.2 Thruster’s Operation
The MINAKA thruster uses a cluster of radioisotope propulsive cells (RPC)
composed of interconnected radioisotope electron sources (RES) to produce large
thrust levels. Diagram 92 illustrates the power configuration and geometry of such
RES. They are positioned around a discharge chamber and connected to an
acceleration grid to form RPCs as illustrated in Diagram 93. Diagram 94
illustrates the operation of a RPC. When switched off the discharge chamber can
either be left flooded with radiations or a radioisotope cover could be placed
between the radioisotope heat source and the EVM. During operation, the EVM is
first activated to decelerate electrons down to their optimal ionization energy then
neutral gas is injected into the discharge chamber. Once ionization has taken place,

117. BUAA Academic Dissertation for Doctoral
81
ions are extracted out of the discharge chamber by a potential difference to
generate the beam. This potential difference equal to the beam voltage is
established between the anode wall and the accelerator grid. The ion beam leaving
the discharge chamber will finally generate the thrust of the RPC.
Diagram 92 Power Configuration and geometry of a Radioisotope Electron Source (RES)
Diagram 93 Geometry of a Radioisotope Propulsive Cell (RPC) based on which the
thrust, radioisotope mass and excess power densities are calculated

118. Chapter 3 decay radioisotope electron source
82
Diagram 94 Operation of a Radioisotope Propulsive Cell (RPC)
RPCs are very scalable because they operate as individual and self-sufficient
propulsive units and the thrust levels achievable simply depend on the maximal
surface area deployable. When used individually they can achieve thrust levels of
the order of several micro-newtons and can reach far great thrust levels when
operated in clusters. Diagrams 77 to 79 show the thrust levels achievable by
square meter large panels of RPCs using different radioisotopes. These values of
thrust, mass and excess power densities where calculated using the RPC geometry
given in Diagram 93. The thickness of the RES was assumed to be equal to 1 cm,
i.e.: the thickness of the radioisotope heat source, but will in practice be much
greater because the thickness of the RTG module and EVM were not taken into
consideration. It can be seen that a single square meter large panel covered with
RPCs can achieve thrust levels of several milli-newtons that are equal and
sometimes even larger than the ones of conventional ion and hall thrusters.

119. BUAA Academic Dissertation for Doctoral
83
Although these RPC panels are much larger than conventional ion thrusters’
diameter, they have the advantage of being very compact and could be operated
and deployed in space similarly to conventional solar panels as illustrated in
Diagram 95. These RPC panels would however be much heavier than
conventional solar panels but they would have the advantage of being able to
generate thrust in addition to not negligible amounts of power.
Diagram 95 Deployment of RPC panels fitted on a communication satellite

120. Chapter 3 decay radioisotope electron source
84
3.8.3.3 Assumptions Consideration
Although the assumptions made to describe the physics of the MINAKA thruster
are not completely accurate they yet remain reasonable and give an approximate
picture of its operation. These assumptions will now be discussed in order to
understand their repercussions on the thruster’s operation and performance.
The radioisotope decay was assumed to be isotropic but it is in fact anisotropic and
random. The decay rate introduced in Eq. 3.1 only gives a statistical idea of the
decay process and is not completely precise. This will impact the degree of
ionization hence the thrust generated by a RPC. Single micro-thrusters could lose
in precision but the impact of this lack of precision would result in more serious
thrust uniformity problems in large RPC clusters.
The electron decay energy is also concerned. It was approximated by a
homogenous mean decay energy over all electrons but follows in fact a
Maxwellian energy distribution characterized by highly energetic electrons at its
tail. If the EVM voltage were calculated in function of the mean decay energy, the
ionization cross section of the bulk electrons will not be optimal and would result
in lower degrees of ionization. This would also greatly affect the thrust achievable.
The impact of secondary electrons on the ionization process was not taken into
consideration because it was assumed to be less significant than the one of
primary, i.e.: radioisotope, decay electrons. This is generally true for conventional,
larger, ion thrusters but their importance might have been underestimated in this
case where the volume of a RPC discharge chamber is significantly smaller. The
electron path length of primary electrons would exceed the dimensions of the
discharge chamber and their ionizing efficiency would be reduced. This could
therefore enable secondary electrons to have a much larger impact on the
ionization process hence thrust levels achievable.
Eq. 3.20 was based on the assumption that the ion production and loss rates were
equal however the typical neutral density which was chosen might not fulfill this
criterion. This equation also did not depend on gas properties while in fact the gas
density and temperature will have a great impact on the degree of ionization. High

121. BUAA Academic Dissertation for Doctoral
85
neutral density will increase the rate of recombination hence the ion loss rate
whilst high neutral temperature will increase the plasma temperature and ease its
production. This assumption must be maintained in order to prevent the plasma
from either becoming fully ionized or from recombining. Fully ionized plasma
temperatures exceed the melting point of terrestrial materials and are hard to
confine without using powerfully magnetic fields and a recombined plasma , i.e.:
neutral gas, cannot be electrostatically accelerated.
Most of these assumptions will have a critical impact on the thrust generated by
RPCs but could easily be palliated if the degree of ionization were known. In the
event of an increase or decrease in degree of ionization, a control system could
easily adjust the beam voltage to maintain a constant thrust. This can be
accomplished using Langmuir probes. A micro Langmuir probe placed inside a
RPC’s discharge chamber could provide such information and help adjust the
beam voltage so as to achieve precise thrust levels in micro-thrusters and keep the
total thrust of large RPC clusters uniform.
3.8.3.4 Plasma Confinement
Although it could confine plasma using magnetic fields similarly to conventional
ion thrusters the MINAKA thruster uses an electrostatic field in order to reach
better propulsive performances. Permanent magnets could be used to confine the
discharge chamber plasma in a MINAKA thruster operating with a single ionizing
side but this would however greatly limit the neutral gas ionization hence thrust
levels achieved by the device. MINAKA thrusters operating with four ionizing
sides use their EVMs to confine the plasma. The negative potential surrounding
their downstream grids is extremely high, i.e.: of the order of several kilovolts, and
creates a negative potential cage that confines the cold plasma by isotropically
repelling its electrons towards the centre of the discharge chamber.
3.8.3.5 Performance Characteristics
The number of ionizing sides and electric conversion efficiency greatly influenced
the propulsive performance of the MINAKA thruster but only up to a certain
point. It can be seen from Diagrams 28 to 59 that the thrust levels and degree of

122. Chapter 3 decay radioisotope electron source
86
ionization increase with the number of ionizing sides and electric conversion
efficiency. Both parameters are respectively limited by the geometry of the
discharge chamber and the minimum electric conversion efficiency. As previously
explained out of the six sides of the cubic discharge chamber, two must be
allocated to the neutral gas injection and ion extraction processes leaving a
maximum of four sides for the ionization process. The four side ionization
geometry enables the generation of more uniform plasma hence limits energetic
losses. The minimum electric conversion efficiency was calculated from the power
required to simultaneously operate the EVM and the accelerator grid hence setting
the requirement for the thruster to be self-powered. For a given beam voltage, any
additional power would be considered as excess power that can be used to power
the different subsystems of the spacecraft. It can also be seen from Diagrams 77 to
82 that the degree of ionization and radioisotope density also greatly influence the
thrust and radioisotope mass densities. Radioisotopes with high degrees of
ionization achieved the best thrust densities whilst the ones with low densities
minimized the radioisotope mass density. The best propulsive performances were
achieved in an optimal range of discharge chamber length starting from to
. It should also be noted that the thrust densities achieved by the MINAKA
thruster easily compare with the thrust levels of conventional ion thrusters. Power
Consideration
The MINAKA thruster is self-powered and even generated non negligible amounts
of electric power using electric conversion efficiencies close to its minimum self-
powered operating point. The thruster even reached excess power densities of a
few kilowatts within its optimal operating range. This additional power supply
could be used to partially or completely power the systems of its spacecraft.
Diagram 76 shows the minimum electric conversion efficiency of the selected
radioisotopes and it can be seen that different types of RTG must be used to
achieve them. The operation of MINAKA thrusters using and can
unfortunately not be optimal because its minimum electric conversion efficiency
exceeds the one of the best performing type of RTG.

123. BUAA Academic Dissertation for Doctoral
87
3.8.3.6 Performance Comparison
The minaka thruster distinguishes itself significantly from conventional ion
thrusters such as the NSTAR or NEXUS ion thrusters thanks to its energetic self-
sufficiency. While conventional ion thrusters require external power inputs to
operate, the Minaka thruster meets its own power requirements by converting the
heat generated by its radioisotope source into electricity using a radioisotope
thermoelectric generator.
This said it could however be useful to establish a set metrics to gauge the
performance of the Minaka thruster against the ones of conventional thrusters. The
thrust generated by the Minaka thruster per unit area and power could be
compared to the values obtained by conventional thrusters to this end. Please find
below diagrams illustrating this comparison. Thullium-171 was selected to power
the Minaka thruster because of its superior thrust performances.
Diagram 96 Thrust to Area ratio of the Minaka and other conventional ion thrusters

124. Chapter 3 decay radioisotope electron source
88
Diagram 97 Thrust to Power ratio of the Minaka and other conventional ion thrusters
It can be seen on the diagram 1 that the Minaka thruster poorly compares with
existing conventional ion thrusters when it comes to the amount of thrust produced
per unit area. A much larger propulsive surface would therefore be required in
order to match the same thrust levels as conventional ion thrusters. This could be
disregarded since space is exactly what is abundant in “space”, where the use of
larger deployable propulsive surfaces could easily be accomplished. Additionally,
diagram 2 reveals that for low values of discharge chamber length, the Minaka
proves much more energy efficient than conventional ion thrusters. This fact is
significant since this range of discharge chamber lengths corresponds to the
thruster’s optimal operating geometry, i.e.: see diagram 59. Past that point the
propulsive efficiency of the Minaka thruster drops below the ones of conventional
ion thrusters however it should be noted that while having an inferior propulsive
efficiency, the Minaka thruster still generates a significant amount of excess power
on top of the power required for its own operation. This demonstrates that the
Minaka thruster not only is a viable alternative to conventional ion thrusters but it
also brings greater benefits to spacecraft by covering on one hand its own power
requirements and by generating on the others significant excess power. Space
missions operating in regions of low solar density such as space probes or

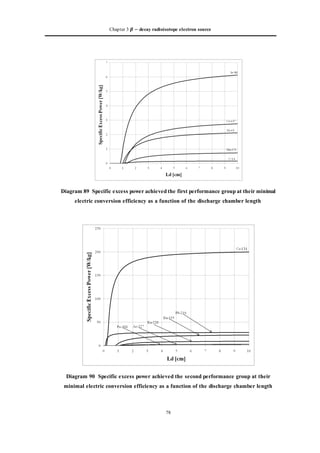
125. BUAA Academic Dissertation for Doctoral
89
requiring great power supply such as earth observation and telecommunication
satellites could greatly benefit from its use.
No special description of the ISP of the Minaka thruster was given because its
beam voltage was chosen to be equal to the one of the NSTAR thruster, i.e.:1100
[V], in order to obtain comparable results. Other conventional ion thrusters use
similar beam voltages for performance reasons. Larger beam voltages hence
specific impulses could be achieved by the Minaka thruster because the excess
power that it generates could be used to increase its thrust however doing so would
have resulted in severe long performances reduction due to material wear and
erosion.
3.8.3.7 Applications
The application of the MINAKA thruster mainly depends on the required mission
duration and each type of duration, i.e.: long or short, brings different advantages.
Mission durations are set by the selected radioisotope’s half-life. A 6 year mark
will arbitrarily be chosen and radioisotopes with half-lives exceeding this mark
will be preferred for long duration missions whilst those with shorter half-lives
should be used on short duration missions.
These last missions which are similar to the ones of Automated Transfer Vehicles
(ATV) or Earth Observation Satellites (EOS) could be accomplished by MINAKA
thrusters using either , , , , , or .
These radioisotopes are characterized by high thrust densities and specific excess
power generations. High thrust densities are important for those two applications
because ATVs and EOSs require great thrust levels to respectively, deliver cargo
or tug payloads to higher orbits, and sustain a stable orbits in the higher drag
environment that are lower earth orbits. Their higher specific excess power
generation would enable them to cover significant portions of their power
requirements and even be completely self-powered.
Longer duration missions such as the ones of space probes and communication
satellites could be accomplished by MINAKA thrusters using either
, , , or . Although these thrusters these radioisotope

126. Chapter 3 decay radioisotope electron source
90
achieved lower thrust levels and specific power generations this self-powered
electric space propulsion systems would however benefit them by helping greatly
extend their operating life and range. Ion thrusters require much less fuel than
conventional chemical engines to achieve a given delta-v because they have much
greater specific impulses. Their use is however limited by their power
requirements. MINAKA thrusters do not suffer from such power constraints and
using them on communication satellites would enable them to be more profitable
while space probes could travel much further into deep space especially in regions
of low solar power densities.
3.8.3.8 Advantages & Disadvantages.
The MINAKA thruster has several advantages over conventional ion thrusters. It
saves a considerable amount of power, is very scalable and compact. This thruster
produces its own electricity and therefore does not rely on the spacecraft power
supply. The excess electricity that it genereates could additionally be used to
partially or completely power the spacecraft. The MINAKA thruster is composed
of several independent RPCs and can thus achieve thrust levels ranging from a few
micro-newtons up to several milli-newtons. As opposed to conventional electric
propulsion systems achievable thrust levels are not limited by the spacecraft power
generation but solely depend on the rocket initial launch capability. The
compactness of RPC panels limits the influence of MINAKA thruster’s volume on
the thrust levels achievable by a spacecraft and makes them solely depend on the
rocket’s maximal payload mass.
The thruster also has two main disadvantages. It is heavier and potentially more
hazardous than conventional ion thrusters. First the required mass of radioisotope
can be very large and finally radiations emitted by them are very hazardous and
could either harm nearby operators or damage surrounding equipments.
3.8.3.9 Radioisotope Production Consideration
The radioisotopes required to operate the Minaka thrusters have different levels of
manufacturing difficulty. Some radioisotopes are fission products and can directly

127. BUAA Academic Dissertation for Doctoral
91
be extracted from nuclear waste. Others are harder to manufacture because they
must be synthetized through the thermal neutron ionization of a target element.
Additionally, some radioisotopes are only found in trace elements and must be
painstakingly gathered through enrichment processes, obtained through
radioactive decay or from environmental sources.
The production processes required by the radioisotopes used in the Minaka
thruster are detailed in the table 3.
3.8.3.9.1.1.1.1 Table 3 Radioisotope production processes and ease
Radioisotope
Natural
Abundance
Production
Method
Target/Source
Target Abundance
/Fission product
Yield/mother
nuclide half-life
Ease of
Manufacture
Carbon-14 trace
target neutral
irradiation
Nitrogen-14 99.634% easy
Cesium-137
synthetic
element
Nuclear Reaction
by product
Uranium-235 6.3% easy
Samarium-151
synthetic
element
Nuclear Reaction
by product
Uranium-235 1.1% easy
Strontium-90
synthetic
element
Nuclear Reaction
by product
Uranium-235 5.6% easy
Nickel-63
synthetic
element
target neutral
irradiation
Nickel-62 3.66%
hard (difficult
separation
from other
radioisotopes)
Actinium-227 trace
target neutral
irradiation
Radium-226 trace hard
Lead-210 trace
target neutral
irradiation/sea
water extraction
Radium-226 trace hard
Radium-228 trace
radioactive
decay
Thorium-232 /
Actinium-228
100% & 1.4e10
(years) / trace &
6.13 (hours)
hard
Cesium-134
synthetic
element
Nuclear Reaction
by product
Uranium-235 6.7% easy

128. Chapter 3 decay radioisotope electron source
92
Europium-155
synthetic
element
Nuclear Reaction
by product
Uranium-235 0.03% medium
Thallium-204 trace
target neutral
irradiation/
ground water
extraction
Thallium-203 29.5% easy
Promethium-
147
trace
Nuclear Reaction
by product/
target neutral
irradiation
Uranium-235/
neodymium-146
2.4%/29.5% easy
Osmium-194
synthetic
element
target neutral
irradiation
osmium-192 41% easy
Antimonium-
125
synthetic
element
Nuclear Reaction
by product
Uranium-235 0.0297% medium
Thullium-171
synthetic
element
target neutral
irradiation
Erbium-170 14.9% easy
Many radioisotopes used by the Minaka thruster can be relatively easy to
manufacture because they can abundantly be harvested from nuclear waste or
because they can be produced through the irradiation of relatively abundant
targets. The production of other radioisotopes was found more challenging due to
the much lower availability of sources.
3.8.3.10 Mass & Radiation Considerations
The radioisotope density has a great influence on the radioisotope mass density
and low density radioisotopes such as , and could help keep the
MINAKA thruster lightweight. This is particularly important for mass sensitive
applications such as commercial satellites. Using a self-powered electric space
propulsion system would enable them to save a great quantity of fuel but this
saving would be offset by the mass increment that some well performing yet high
density radioisotopes such as and would induce. Although the
thruster would still be of interest for scientific missions, its added weight would
deter any commercial applications because weight and cost are interchangeable in

129. BUAA Academic Dissertation for Doctoral
93
commercial space applications. Communications satellite manufacturers would
therefore only see the Minaka thruster as a hazardous and cost ineffective
innovation.
Radiations must also be taken into account since the shielding required would also
greatly influence the thruster’s weight. Table 4 gives the shielding required by the
selected radioisotopes. MINAKA thrusters using radioisotopes with low
radioisotope mass densities such as would in fact be much heavier because
of their shielding requirements. Using other radioisotopes such as
might be totally impractical regardless of their promising performances
because they might just be too dangerous to handle or shield. The EVM will also
generate some bremsstrahlung radiations by decelerating electrons which will
therefore further increase the radiation shielding requirements.

130. Chapter 3 decay radioisotope electron source
94
3.8.3.10.1.1.1.1 Table 4 Approximate lead shielding required for radioisotope sources for [ ] at
Radioisotope
Decay
type
Decay Energy
(keV)
Half-Life
(yr)
Compound form
Melting Point
(°K)
Watt per gram Curies per watt
Pb Shield
Required (in.)
Ca (pure)
CsCl 918 0.12 207 4.6
76.7 90 Sm (pure)
[40]
Ni (pure)
45 21.8 Ac (pure) 1323 1.74 45.3 0.01
Pb (pure)
46 5.8 Ra (pure) 973 0.0741 2200 0.0
21 14.35 2673 0.0127 1.73e4 0.0
CsCl
Eu (pure)
Th (pure)
Pm (pure)
Os (pure)
Sb (pure)
Tm (pure)
* radiation shielding calculated over entire decay chains, i.e.: including gamma decays of daughter nuclides

131. BUAA Academic Dissertation for Doctoral
95
3.8.4 Validation of the Simplistic model using Numerical Simulation
3.8.4.1 Introduction
The performance characteristics obtained using the simplistic ionization model
developed in section 3 could be used to obtain an approximate picture of the
performance of the Minaka Thruster but are not fully reliable because they omit
several plasma physical phenomena.
A better understanding of the operation of the thruster could be obtained thanks to
numerical simulations and the aim of this section is to create a simple numerical
model that will be used to validate or negate the results obtained by the simplistic
ionization model.
The commercial plasma simulator, Oopic Pro version 2.0.2, will be used to this
end. It was developed Tech-X Corporation and is based on the plasma simulator,
Xoopic, an well-known object oriented PIC code written in C++ developed by the
Plasma Theory and Simulation Group at the University of California, Berkeley.
3.8.4.2 Model Construction & Parameters
Oopic enables two types of geometry, Cartesian and cylindrical. The axes x1, x2
and x3 of the simulation respectively refer to the x, y and z axes in a Cartesian
geometry and z, r and in a cylindrical geometry. The x3 axis hence z and axes
is the simulator axis of symmetric and is therefore always equal to unit. All units
used in the simulation are expressed in the meters, kilograms, seconds (MKS)
system.
The selected geometry matches the cubic volume of the Minaka thruster’s
discharge chamber as illustrated in Diagram 98. The x1 and x2 axes can be
modified in the simulator to suit a required geometry however the x3 axis being
the axis of symmetry cannot be altered and will always remain equal to ].
Caution must therefore be used when setting the radioisotope electron currents.
The value provided in the simulator should be amended to taken the invariable
length of the x3 axis into account in order to return sound values.

132. Chapter 3 decay radioisotope electron source
96
Diagram 98 geometry of the Minaka Discharge chamber
Oopic can simulate a wide range of boundary conditions which transparency and
degree of reflection can easily be adjusted. Such boundaries will later be explained
as used in the simulation but there simplicity will however be maintained in order
to obtain the simplest simulation configuration possible.
3.8.4.2.1 Data Visualization
Oopic provides 2D and 3D diagnostic plots. 2D figures are often used to illustrate
the motion of simulation particles while 3D plots are used to illustrate the spatial
distribution of particles. Diagrams 99 and 100 illustrate examples of 2D and 3D
diagnostic plots. Oopic can additionally plot curves that represent the number of
particles at any given moment in time as illustrated in diagram 101. Oopic
illustrates ALL simulated particles in 2D, 3D and curve plots which means that all
particles present in the 3D geometry illustrated in diagram 98 will always be
shown on a 2D illustration. Since this number is often very high, macro-particles
are therefore frequently used. These simulated particles represent several orders of
real particles. The ratio between the number of simulated macro-particles and real
particles, i.e.: denominated MacPar in the Oopic code, can easily be set.
Remember that only simulated, i.e.: often macro-particles, particles are given
within all diagnostics plots and that 2D plots illustrate ALL simulated particles

133. BUAA Academic Dissertation for Doctoral
97
present within the 3D numerical model. Care should therefore be taken when
calculating number of real particles generated within the simulation by
appropriately multiplying the number of simulated macroparticles by the macro-
particle ratio and by dividing this number of particles by an appropriate factor that
takes the unit x3 symmetric axis into consideration.
Diagram 99 Example of a 2D particle diagnostic plot
Diagram 100 Example of a 3D particle distribution diagnostic plot

134. Chapter 3 decay radioisotope electron source
98
Diagram 101 Example of a plot representing the time variation of the number of
simulated particles
Oopic uses a programming language to building simulation environments. More
details on this programming language can be found in the User’s guide of Oopic
Pro version 2.0.0. Parameters must be set to control the simulation, grid, particles
and boundaries but the ones of the greatest importance in this simulation work will
be the electron current coming from all four ionizing sides, the electron velocity,
neutral gas pressure and real particles to macro-particles ratio. No neutral flow is
injected into the discharge chamber since this investigation primarily focuses on
the ability of radioisotopes to ionize neutral gas. The codes used to run the
simulations can be found in appendix A.
3.8.4.3 Neutral gas Ionization without electron confinement
The ionization process taking place inside the Minaka thruster will be numerically
investigated and verified in this section. Two configurations will be considered.
The first one will simulate the neutral gas ionization that would take place if
electrons were not confined inside the discharge chamber, i.e.: if they were
allowed to cross from boundary of the discharge chamber to another. The second
case will consider the neutral ionization when electrons are electrostatically
confined into the discharge chamber by the high negative voltage of the
downstream grid of the EVM. Both simulations aim to evaluate the accuracy of

135. BUAA Academic Dissertation for Doctoral
99
the simplistic ionization model presented in section 3 by giving a gradually more
realistic picture of the ionization process taking place inside the Minaka Thruster.
The performance characteristics of a Minaka thruster using a Thullium-171 will be
numerically simulated and then compared to the ones obtained using the simplistic
ionization model developed in section 3, see diagrams 43 and 59.
The key simulation parameters are summarized below in table 5.
3.8.4.3.1.1.1.1 Table 5 Simulation Parameters for Thulium-171 induced neutral gas ionization
Parameter Values
Electron Current Density [I/ ] 1e-5
Electron Velocity 3.25e6
Neutral Gas Pressure assuming
a typical neutral density of [ ]
And temperature of 300 [
6e-5
This numerical model is relatively simple. There are electric nor magnetic fields
involved, no electrostatic confinements and radioisotope electrons can therefore
freely cross and exit the discharge chamber from one boundary to another while
ionizing the background neutral gas.
It quickly became evident that many of the assumptions and predictions made
during the development of the simplistic ionization model were correct. It can first
be seen from diagram 102 that the geometry of the Minaka led to perfectly
uniform ionization pattern. Electrons simultaneously enter the discharge chamber
and progressively fill it until saturation is achieved after what the electron density
inside the discharge chamber remains constant as it can be seen from diagram 103.
This occurs because all electrons have achieved a state of equilibrium from which
electrons entering the discharge chamber perfectly match those exiting it. This

136. Chapter 3 decay radioisotope electron source
100
constant and uniform electron discharge generates an equally uniform and constant
ion production as it can be seen in diagrams 104 and 105. This constant ion
production rate is a very important factor because it enabled us to reliably predict a
steady state, i.e.: after 1 minute, ion count hence degree of ionization.
Diagram 102 Uniform ionization pattern inside the Minaka thruster discharge chamber

137. BUAA Academic Dissertation for Doctoral
101
Diagram 103 plot of electron count over time (blue line)
Diagram 104 uniform ion density

138. Chapter 3 decay radioisotope electron source
102
Diagram 105 constant ion production rate (green line)
The ionizing process inside the discharge chamber of the Minaka thruster was
subsequently simulated for different values of discharge chamber length and
temperatures to plot new performance curves for Thulium-171. A new neutral gas
density value was calculated for a constant typical gas temperature of [ ] in
order to account for the change in pressure using the following expression:
(3.40)
Where is the neutral gas temperature. The new degree of ionization and thrust
density plots of Thullium-171 which include curves numerically simulated and
calculated using the simplistic ionization model are illustrated in diagrams 106 and
107. The simulated data plots used to generate these curves are listed appendix B.

139. BUAA Academic Dissertation for Doctoral
103
As predicted the numerical simulation returned superior to the ones achieved by
the simplistic ionization model but both ionization profile do not match. It is
nevertheless comforting to see that the simplistic ionization model returned
performance characteristics of the right order of magnitude.
At low values of discharge chamber length, numerical simulated performances
were in average 170% larger than the ones expected by the simplistic model. This
is understandable because this last model did not take into consideration all
physical principles into account and was built on major simplifying assumptions.
The impact of secondary electrons, particle interactions and the possible lack of
ionization equilibrium all must have played a great impact on increasing the effect
of ionization. Furthermore the degree of ionization does not seem to sharply
decrease for large values of discharge chamber length as predicted by the
simplistic model must remains relatively constant even for high values of
discharge chamber length. This phenomena is hard to explain and could either be
due to the higher temperature generated by ionized and excited ions or to
computational instabilities. The ratio of macroscopic particles to real particles used
in larger values of discharge chamber length coupled with relatively small spatial
steps could have caused these great variations from the expected profile. The
neutral gas temperature assumed in these simulations might not be appropriate due
to the high degree of ionization achieved when compared with the bulk of plasma
of conventional discharge chambers which could lead to believe that even higher
levels of degree of ionization should be expected.
This supposition is confirmed by diagram 108 which illustrates the evolution of
the thruster performance characteristics with increasing pressure levels. It can be
seen that the simulation returned similar degrees of ionization and thus over
several orders of magnitude of neutral gas pressure before abruptly dropping as the
pressure neared the mark of the . This could mean a sudden
thermalization of the plasma coupled with a sharp increase in thrust density. These
numerical results could be due to simulation error but their consistency over a
reasonable range of operation for ion thrusters point to the contrary. This could

140. Chapter 3 decay radioisotope electron source
104
also lead us to believe that the Minaka Thruster could optimally be used at much
greater pressure levels than conventional ion thrusters.
Although the simulation results may somewhat be unexpected, they nevertheless
support the main goal purpose of this investigation, i.e.: the feasibility study of the
use of radioisotope based electron sources for space applications.
Diagram 106 variation the degree of ionization achieved by Tm-171 with discharge
chamber length using different models and at different neutral gas temperatures

141. BUAA Academic Dissertation for Doctoral
105
Diagram 107 variation the thrust density of Tm-171 with discharge chamber length
using different models and at different neutral gas temperatures
Diagram 108 Variation of the degree of ionization and thrust density with the neutral
gas pressure
3.8.4.4 Neutral gas ionization with electron confinement
As the former ionization model aimed to gauge the ionization potential of
radioisotopes by building the simplest model, the following simulation aims to
build a more realistic model where electrons would be confinement into the

142. Chapter 3 decay radioisotope electron source
106
discharge chamber by an electrostatic field created by the downstream grids of the
EVM. It quickly appears from diagram 109 that such configuration would
completely ionize the background because of the exponential growth profile of the
ion count. diagram 110 shows that the electron count does not top up at a certain
value but continues to increase throughout the simulation causing a cascade of
ionization that drastically modified the ion production rate profile. This future
reinforces our conviction that the Minaka thruster is not capable of effectively
ionizing neutral but does so with an extremely high effectiveness with compared
with conventional ion thrusters and thus at no added energetic cost. The plasma
and neutral gas temperature achieved this device are hard to predict but should
prove to be rather consequent and these were apparently completely ignored by the
simplistic ionization model.
Diagram 109 Exponential growth profile of the ion count in electron confined ionization
model

143. BUAA Academic Dissertation for Doctoral
107
Diagram 110 Linear and uninterrupted growth profile of the electron count in electron
confined ionization model
These simulations are very promising but should be taken with caution because the
numerical models suffered from great limitations. The academic version of Oopic
Pro used in this investigation is rather constrained and limits the depth of
application of the software package. Complete and demanding simulations are not
impractical and steady state results have to be extrapolated from linear or
exponential trends. However the simplicity of these models should play in their
advantage and if not predict accurate performance characteristics confirm trends.
The greatest shortcoming of these numerical simulations is complete absence of
experimental
3.8.4.5 Conclusion
It can therefore be concluded that although precise results could hardly be
obtained using the present numerical models, they nevertheless through their
relative simplicity first support the validity of the results obtained using the
simplistic ionization model and finally confirm the thesis of this present work, i.e.:
the feasibility of the use of radioisotope based electron sources in space
applications. Experimental investigations should therefore be carried as a next step
in order to further our understanding of the physical processes taking place in the

144. Chapter 3 decay radioisotope electron source
108
device, i.e.: neutral gas ionization, electric field interaction, heat generation and
dissipation, etc, and to precise its performances.

145. BUAA Academic Dissertation for Doctoral
109
4 Radioisotope Heated Thermionic Electron Source
The development of a radioisotope heated thermionic electron source will now be
outlined then its applications will be explained.
4.1 Thermionic Emission
Thermionic emissions occur when a given emitting materials is brought to a
sufficiently high temperature. Once the material work function, i.e.: electron
emission energy, is achieved some materials will start emission significant
electron currents as illustrated in Diagram 111.
Diagram 111 thermionic emission of a light bulb
These emissions are described by the Richardson-Dushmann equation[41]:
⁄
(4.1)
where is a constant that is ideally equal to ⁄ , is the
temperature in kelvins, is the work function and is the Boltzmann’s constant.
Eq. (4.1) is not always applicable because its parameter may vary due to surface
and microscopic characteristics. This problem was later solved by substituting it

146. Chapter 4 Radioisotope Heated Thermionic Electron Source
110
with a new constant which takes a temperature correction factor into
consideration.
⁄
(4.2)
Values of thermionic parameters and emission current densities will next be
discussed. Table 6 shows values of both constants and of the work function of
different emitter materials and Diagram 112 illustrates plots of thermionic
emission current densities versus the emitter’s temperature. These plots were
calculated using Eq. (4.2) and the different parameters given in Table 6.
Temperatures exceeding 700 K are necessary to achieve useful thermionic
emissions and a wide range of thermionic emission current densities is also
possible. Materials with low work functions, such as Scandate, initiate thermionic
emissions at lower temperature because less energy is required to free electrons.

147. BUAA Academic Dissertation for Doctoral
111
Table 6 Work Function and Richardson coefficients for several cathode materials[2]
⁄ ⁄
Molybdenum
Tantalum
Tungsten

149. BUAA Academic Dissertation for Doctoral
107
Diagram 112 Emission current density versus temperature for various cathode
materials[2]
4.2 Radioisotope
Radioisotope decays are exothermic and can induce radioisotope surface
temperatures of the order of several hundreds and even thousands of degree.
Diagram 112 shows that consequent thermionic electron emissions could be
initiated through direct contact with such radioisotope heat sources and this new
method would have the advantage of not requiring any electricity because
radioisotopes naturally decay.
Suitable radioisotopes should therefore be selected to guarantee the good operation
of this radioisotope heated hollow cathode and those currently used to power
RTGs would be the most appropriate ones because they combine high decay heats,
low gamma emissions and long half lives. High decay heats would minimize the
quantity of radioisotopes, low gamma emissions would minimize the thickness of
the radiation shielding and long half lives would enable the operation of this
hollow cathode over the duration of most space missions. Strontium-90 ( ,
Plutonium-238 ( and Curium-244 ( are such radioisotopes. Tables 7
and 8 give the characteristics of the selected radioisotopes, their shielding
requirements and emission current densities.

151. BUAA Academic Dissertation for Doctoral
109
Table 7 Radioisotope characteristics and lead shielding required for radioisotope sources for a target exposure of [ ] at [39]
Radioisotope
Decay
type
Decay
Energy
Half-Life
[yr]
Compound
form
Melting Point Density
[
Watt
per gram
Curies per
watt
Pb Shield
Required
546 28.0 2313 4.6 0.22 148 6.0
5593 87.7 2673 10.0 0.39 30 0.1
5901 18.1 2453 9.0 2.27 29 2.0
Table 8 Thermionic emission current densities for Strontium-90, Plutonium-238 and Curium-244 using different insert materials
Surface
Temperature
[K]
Thermionic Emission Current ⁄
[42]
[43]
[44]
*average values.

153. BUAA Academic Dissertation for Doctoral
111
4.3 Thermal Reductive Layer
Precise thermionic emission current densities cannot be achieved using
radioisotope heat sources because their surface temperatures cannot be modulated
but thermal reductive layers could solve this problem. These layers are located
between radioisotope heat sources and emitter materials and act as buffers that
reduce the surface temperature in direct contact with the emitter material. A
thermal reductive layer has a known thermal conductivity and increasing its
thickness precisely decreases the temperature of its cold surface. This thickness
can be calculated using the equation of conductive heat transfer:
(4.3)
Where is the thermal conductivity of the thermal reductive layer, is the
temperature of the hot surface, is the temperature of the cold surface, is the
thickness of the thermal reductive layer and is its surface area. After
introducing a heat flux, i.e.: , Eq. (4.3) can be rearranged to give the thermal
reductive layer thickness required to achieve a precise temperature at its cold and
unexposed surface:
(4.4)
Diagram 113 illustrates a thermal reductive layer. Such layer can only be used at
the condition that the target temperature of the emitter material is lower than the
one of the radioisotope heat source. The difference between the target and
radioisotope heat source temperatures should be minimized to keep the hollow
cathode compact since thinner thermal reductive layers will be required.

154. Chapter 4 Radioisotope Heated Thermionic Electron Source
112
Diagram 113 thermal conduction between a heat source (dark grey) and an emitter
material (light grey) through a thermal reductive layer (diagonals) of a given thickness
and thermal conductivity
4.4 Applications
This Radioisotope Heated Thermionic electron source can be used to generate
plasma. Plasma generators have numerous applications and could be used as a
plasma source for most space propulsion systems. Hollow cathodes and plasma
rocket engines were selected as the first applications of this new technology and
the results achieved through its use will now be displayed and discussed.
4.4.1 Hollow Cathode
4.4.1.1 Calculations
4.4.1.1.1 Power Requirement
Additional benefits can be brought by applying the Self-Sufficiency Principle.
This radioisotope heated hollow cathode could achieve a state of self-sufficiency
by first naturally heating up its insert material with its radioisotope decay heat and
then powering its keeper electrode with the electricity generated from its own
decay heat using a RTG. The radioisotope mass required in Eq. 2.1 to achieve a

155. BUAA Academic Dissertation for Doctoral
113
self-sufficient state can be found by first equating the target power generation to
the cathode keeper power:
(4.5)
The discharge cathode keeper power is given by:
(4.6)
where is the discharge cathode keeper current and is the discharge cathode
keeper voltage. The radioisotope power generated per unit mass can be obtained
by using the following expression:
(4.7)
The required radioisotope mass is given by:
(4.8)
and the required radioisotope volume is equal to:
(4.9)

156. Chapter 4 Radioisotope Heated Thermionic Electron Source
114
Diagram 114 illustrates a simplified schematic of an emitter segment showing the
geometries of a hollow cathode tube and radioisotope heater. The emitter length,
, cathode tube diameter, , and radioisotope heater diameter, , are given. It
can be seen that the radioisotope volume is given by:
. (4.10)
Equating Eqs. (4.9) and (4.10) then solving yields the radioisotope diameter:
√ .
(4.11)
Diagram 114 Simplified representation of the emitter segment of the hollow cathode
tube and of the radioisotope heat source where the emitter length, , cathode tube, ,
and radioisotope heater diameter, , are indicated

157. BUAA Academic Dissertation for Doctoral
115
4.4.1.2 Results
The performance of this radioisotope heated hollow cathode was assessed using
the configuration of two ion thrusters as benchmark. These configurations were
the 15th throttle of the Nasa Solar Electric Propulsion Application Readiness
(NSTAR) thruster and the maximal power configuration of the Nuclear Electric
Xenon Ion System (NEXIS) thruster which were respectively denoted “NSTAR-
TH15” and “NEXIS-MAX”.
Table 9 shows all the relevant geometric, mass and power characteristics of both
benchmark configurations and table 10 gives the performance achieved by this
hollow cathode. Eq. 4.11 was mainly used to derived the results of table 10.

159. BUAA Academic Dissertation for Doctoral
117
Table 9 Power and geometric characteristics of the NSTAR-TH15 and of the NEXIS-MAX configurations
Parameters NSTAR - TH15 NEXIS-Max
emitter length, , [45] [45]
Hollow Cathode tube diameter, , [45] [45]
Thruster Diameter, , [46] 65 [47]
Thruster’s mass, , [kg] [36] 37.5 [48]
discharge cathode keeper current, , [A] [46] [47]
discharge cathode keeper voltage, , [49] [47]
RTG conversion efficiency, , [] 5.0% 5.0%
Total Engine Power, , [50] [47]
Table 10 Performance characteristics of the radioisotope heated hollow cathodes when applied to the NSTAR-TH15 and NEXIS-MAX
configurations
Performance Characteristics NSTAR - TH15 NEXIS-MAX
Specific Power, ,
Density, ,
Required Radioisotope Diameter, , [cm]
Tube Diameter Factor, ⁄ ,
Overall Diameter Ratio, ⁄ ,
Required Radioisotope Mass, , 10.9
Mass Ratio, ⁄ , []
Power saved, ,
Overall Power Saving Ratio, ⁄ , 0.5%

161. BUAA Academic Dissertation for Doctoral
119
4.4.1.3 Discussion
4.4.1.3.1 Novel Type of Hollow Cathode
It was demonstrated in this work that radioisotopes can be used to replace hollow
cathode heaters to simultaneously provide heat and power to the device.
Such combination of a radioisotope heat source and RTG is truly innovative and
led to the invention of a totally new type of hollow cathode which was named the
“Kabila” cathode in honor of the late, Laurent-Désiré Kabila, hero and former
president of the Democratic Republic of Congo.
Since the Kabila cathode was developed following the Self-Sufficiency Principle
its operation had to be guaranteed independently from other subsystems and
external power supply hence the need to use the heat generated by the radioisotope
in order to power the cathode keeper. Increasing the quantity of radioisotope in
order to fully power the hollow cathode could not be considered because it would
have been similar to creating a RTG instead of a self-sufficient electron source.
4.4.1.3.2 Geometric & Mass Consideration
Both benchmark configurations achieved very large required radioisotope
diameters and It was found that the specific power and density of a radioisotope
exercised a great influence on geometric performances because larger values of
both parameters reduced the required radioisotope volume.
Using compound radioisotopes instead of pure ones would also not bring any
benefits because the larger densities of compound radioisotopes are compensated
by proportionally lower specific powers.
The real diameter of this radioisotope heated hollow cathode will exceed the
required radioisotope diameter because it does not take the RTG module nor any
other equipment that the hollow cathode would need to operate into consideration.
The overall diameter ratio must therefore be limited and an arbitrary upper limit of
20% should be applied in order to guarantee the proper installation of any
additional equipment.

162. Chapter 4 Radioisotope Heated Thermionic Electron Source
120
The required radioisotope mass was also rather high but it could be reduced by
using radioisotopes with higher specific powers.
4.4.1.3.3 Power Consideration
This hollow cathode saves a not negligible amount of power that is equivalent to
the hollow cathode keeper power. Power savings of 3% and 0.5% were
respectively achieved by the NSTAR-TH15 and NEXIS-MAX configurations and
lower power savings were achieved by the latter configuration because its power
requirements were much greater.
4.4.1.3.4 Comparative Studies
Large size ion thrusters achieved better geometric performances than small and
medium size ones because geometric performances depend on the required
radioisotope diameter and also on the discharge chamber diameter. The required
radioisotope diameter mostly depends on the power requirements of the hollow
cathode keeper and since medium and large size ion thrusters have hollow cathode
keeper electrodes of almost similar power requirements larger ion thrusters will
therefore always achieve better geometric performances. However small and
medium size ion thrusters achieved better energetic performances than larger ones
because energetic performances depend on the power requirements of the hollow
cathode keeper electrode and also on the total engine power. As mentioned earlier
the power requirements of hollow cathode keeper electrodes do not vary much
between medium and large size ion thrusters but their total engine power
significantly does. Small and medium size ion thrusters require much less power
than large size ones and will therefore always achieve better energetic
performances.
Radioisotope densities and specific powers greatly influenced the performances of
this hollow cathode because higher values of both parameters reduced the required
radioisotope radius by increasing the power generated per unit volume. Using
more efficient RTGs could also improve the performances of this hollow cathode
but care should nevertheless be taken to insure that using other types of RTG will
not have detrimental effects such as increasing its volume, weight or complexity.

163. BUAA Academic Dissertation for Doctoral
121
4.4.1.3.5 Hollow Cathode Operation
The operation of Kabila cathodes is very similar to the one of conventional hollow
cathodes and only differs to accommodate its continuous heat generation. Diagram
115 illustrates the schematics of both conventional and Kabila cathodes. Since a
heat shield cannot be accommodated in this new type of hollow cathode the
radioisotope heat source must therefore remain in contact with the cathode tube
during operation otherwise the temperature of the insert material will drop below
its thermionic emission point regardless of its internal self-heating processes and
then interrupt its electron emission. Disconnecting the radioisotope heat source
from the cathode tube switches the hollow cathode off by preventing further
conductive heat transfers from occurring. Convective and Radiative heat transfers
should also be prevented for the same reason. The radioisotope heat source must
be divided into two separate halves of a cylinder in order to ease its connection
and disconnection from the cathode tube. A lifting mechanism is required to
accomplish these operations. It needs to be located inside the keeper’s cavity and
must be powered by the RTG in order to keep the hollow cathode self-sufficient.
(a)

164. Chapter 4 Radioisotope Heated Thermionic Electron Source
122
(b)
Diagram 115 Schematic of a conventional[2] (a) and Kabila (b) cathode showing the
cathode tube, insert, heater enclosed and RTG module in an on/off mode enclosed in a
keeper electrode
4.4.1.3.6 Power Supply Configuration
The power supply configuration of Kabila cathodes differs from the one of
conventional hollow cathodes. Diagram 116 illustrates the power supply
configuration of a conventional DC discharge chamber (a) and of one that uses a
Kabila cathode (b). They are almost similar at the sole exception of the heater
supply. A RTG supply was substituted to it in order to power the keeper supply
and so doing render the hollow cathode self-sufficient because no external power
was needed anymore to support its operation.

165. BUAA Academic Dissertation for Doctoral
123
(a) (b)
Diagram 116 Electrical schematic of a conventional DC-discharge ion thruster[2] (a)
and of one using a Kabila cathode (b) with the cathode heater, keeper, RTG and
discharge power supplies
4.4.1.3.7 Advantages & Disadvantages
Saving power is the main advantage of this hollow cathode. 3% and 0.5% overall
power savings were respectively achieved by the NSTAR-TH15 and NEXIS-
MAX benchmark configurations. This hollow cathode also has the advantage of
being scalable. Small and medium size ion thrusters achieved better energetic
performances thanks to their lower power requirements and radioisotopes of high
densities and specific powers yielded better results.
Radioisotope heated hollow cathodes also have disadvantages. They tend to be
voluminous, heavy and potentially hazardous. First the volume occupied by the
hollow cathode must not only include the cathode tube and the radioisotope heat
source but also the RTG module and lifting mechanism. Second the mass of the
radioisotope heat source is very large and will probably cause important mass
increments. Finally radiations emitted by radioisotopes are very harmful and could
either harm nearby operators or damage surrounding equipments.

166. Chapter 4 Radioisotope Heated Thermionic Electron Source
124
4.4.2 Plasma Rocket Engine
4.4.2.1 Calculations
4.4.2.1.1 Rocket Propulsion
As mentioned before, rocket engines generate thrust by accelerating great volumes
of gas at supersonic speeds. These speeds are acquired by high pressure gases
when they are channelled through a converging-diverging nozzle as illustrated in
Diagram 117.
Diagram 117 Converging-diverging nozzle configuration
The thrust generated by rocket engines is given by the following equation:
̇ (4.12)
where ̇ is the mass flow rate and is the exhaust velocity. The specific impulse,
i.e.: ISP, can be found using the following equation:
̇
(4.13)

167. BUAA Academic Dissertation for Doctoral
125
where is the earth gravitational acceleration. The exhaust velocity of an ideal
rocket operated in a vacuum is given by the following expression:
√ (4.14)
where is the ratio of specific heat, is the specific gas constant and
combustion chamber’s temperature. High combustion chamber temperatures
appear to directly impact the ISP. The ISPs and combustion chamber temperatures
of conventional rocket engines are given in below in table 11.
Table 11 ISPs and Combustion Chamber Temperatures of Conventional Rocket
Engines [2]
Rocket Engine Combustion Chamber Temperature ISP
Monopropellant
Solid propellant
Bipropellant
These combustion chamber temperatures are obtained through chemical reaction
but plasmas could also be used to bring propellant to such temperatures and could
potentially reach better performances. Temperature is defined as the degree of
particle agitation and plasma particles achieve much greater temperatures than the
ones of neutral gases because their ions and electrons are already separated hence
can move much more freely. All matter eventually transits to a state of plasma as
they are heated up because the degree of agitation of neutral particles is so high
that the collision between them breaks the molecular bonds that link ions and
electrons. Neutral gas heating is not the only way to generate plasma and gases can
easily be ionized through collisions with an electron current of the right energy.

168. Chapter 4 Radioisotope Heated Thermionic Electron Source
126
Diagram 118 illustrates the schematic of this radioisotope heated plasma rocket.
As previously explained, its geometry is similar to the one of conventional rockets
at the exception of its combustion chamber. It was replaced by a radioisotope
heated thermionic chamber where neutral gas is transformed into plasma through
electron impact ionization. The chamber is composed of an Emitter material,
radioisotope heat source as well as of a radioisotope Thermoelectric Generator
(RTG) and shielding layer which were respectively added to convert residual
decay heat into electricity and attenuate the effect of hazardous radioisotope
radiations. The operation of the components of this rocket will subsequently be
explained and discussed.
Diagram 118 Schematic of the Radioisotope Heated Plasma Rocket Engine
4.4.2.1.2 Mass flow rate
The heating chamber of the plasma rocket transforms neutral gas into plasma
similarly to the insert of a hollow cathode. Assuming that the neutral gas
temperature inside an hollow cathode is equal to [2], the mass flow rate
through a thermionic emitter is given by the cathode flow. Dividing this cathode
flow by the insert diameter gives the mass flow rate density:

169. BUAA Academic Dissertation for Doctoral
127
̇
̇
(4.15)
where ̇ and respectively are the mass flow rate & surface area of a typical
hollow cathode insert. The radioisotope thermionic heating chamber’s diameter
can be found by dividing the require target mass flow rate by the mass flow rate
density:
̇
̇
(4.16)
where ̇ is the target mass flow rate. These two equations can be used to size the
heating chamber of the radioisotope heated thermionic plasma rocket engine.
4.4.2.2 Results
The performance of this radioisotope heated thermionic plasma rocket engine were
assessed using the configuration of the hollow cathode of the 15th
throttle of
NSTAR thruster and the configuration of a 1 N Hydrazine Thruster developed by
AEDS Astrium [51] which was operated on both spacecraft of the Pleiades-HR-1
constellation [52]. Tables 12 to 15 give the data of the 1 N Hydrazine thruster,
hollow cathode of the NSTAR-TH15, noble gases used and of the power
configuration of the thruster and spacecraft. The performances of the plasma
rocket engine are given in tables 16, 17 and Diagrams 119 and 120. All the
equations developed in this paper and the exhaust velocity of an ideal rocket, ISP
equations were used with the data provided in tables 12 to 14 to obtain the
performances of the plasma rocket engine listed in tables 16, 17 and plotted in
Diagrams 119 and 120. Tables 16 provides the mas flow rate and geometric
performances achieved by different neutral gases operated at the combustion
chamber temperature achieved by this plasma rocket engine, i.e.: [2].
Table 17 provides the power savings and mass requirements achieved by different

170. Chapter 4 Radioisotope Heated Thermionic Electron Source
128
neutral gases and then compares them with the 1 N Hydrazine benchmark thruster.
The heating chamber diameter obtained in table 17 is then plotted against the
required thrust in diagram 119 and the Specific impulses achieved by the neutral
gases for different gas exhaust velocities is illustrated in diagram 120.
Table 12 Data of the 1 N Hydrazine Thruster configuration [51]
1 N Hydrazine Thruster Data
thrust
Isp
Nominal mass flowrate
thrust
Table 13 NSTAR-TH15 Data
NSTAR Data TH-15
InsertDiameter [2]
NSTAR Cathode Flow [46]
HollowCathode Neutral Gas Temperature [2]
Emitter Length [45]

171. BUAA Academic Dissertation for Doctoral
129
Table 14 Noble Gas Data
Noble Gas Data Helium Neon Argon Krypton Xenon
Universal Gas Constant -
Molar Mass
Specific Gas Constant
Specific Heat Ratio -
Table 15 Power Related Data
Power Data
Thruster - CatalystBed Heater [51]
Thruster - Valve 16 V DC [51]
Thruster - Valve 28 V DC [51]
Thruster - Valve 28 V DC [51]
Thruster - Total Power
Pleiades-HR-1 - Power Generation - EOL [52]
Pleiades-HR-1 - Mean Power Generation [52]
Pleiades-HR-1 - Instrument Power Requirement [52]
Pleiades-HR-1 - Number of 1 N HydrazineThrusters [52]
Table 16 Mass Flow Rate Performances
Mass Flow Rate Performances Helium Neon Argon Krypton Xenon
Exhaust Velocity
ISP
mass flow rate per orifice
Insert Area
mass flow rate density
Heating Chamber Area [cm^2]
heating Chamber Diameter [cm]

173. BUAA Academic Dissertation for Doctoral
131
Table 17 Power Performances
Mass Flow Rate Performances
Helium
Neon Argon
Krypton Xenon
Selected Radioisotope
Curium-
244
Curium-
244
Curium-
244
Curium-
244
Curium-
244
RTG conversion efficiency
Radiosiotope specific power
[Wt/kg]
Radioiosotope density
[g/cm^3]
Required Radioisotope Mass
Required Radioisotope
Diameter [cm]
Overall Power Saving []
Mean Power Saving []
Instruments Power Saving []
Diagram 119 Radioisotope heated thermionic heater chamber versus the thrust
generated with different neutral gases

174. 132
Diagram 120 Radioisotope heated thermionic plasma rocket engine specific impulse
versus the exhaust velocity with different neutral gases
4.4.2.3 Discussion
4.4.2.3.1 Novel Type of Plasma Rocket
It was demonstrated in this work that radioisotopes can be used in plasma rockets
to thermionically ionize neutral gas and generate electricity.
Such combination of a radioisotope heat source and RTG in a plasma rocket is
truly innovative and led to the invention of a totally new type of plasma rocket
which was named the “Kabila” rocket in honour of the late, Laurent-Désiré
Kabila, hero and former president of the Democratic Republic of Congo.
4.4.2.3.2 Geometric Consideration
The mass flow rate density has a great influence on this radioisotope heated
thermionic plasma rocket engine and it should be reduced in order to achieve

175. BUAA Academic Dissertation for Doctoral
133
better geometric performances. This can be achieved in two different ways. First
the discharge current cathode mass flow was calculated to generate a self-
sustained discharge inside the emitter. However thanks to the use of radioisotopes
such mechanism is not required anymore because heat is continuously being
supplied to sustain thermionic emissions. Neutral gas densities could therefore be
increased without fearing that its temperature may decrease or that the thermionic
emission may be interrupted. Second the diameter of the insert material could be
reduced to improve the geometric performance of the plasma rocket engine. The
values used were based on a continuous operation of the NSTAR thruster hollow
cathode over a period of several years. However hydrazine thrusters are only
required for attitude control and correction and will not be subjected to the same
requirements as the NSTAR thruster’s. Much lower insert diameters are therefore
expected on this new plasma rocket engine and this would yield better geometric
performances. Very little radioisotope is required to power the valves of the rocket
engine but a greater quantity would in fact be needed to quickly initiate thermionic
emissions. The dimensions of the heating chamber nevertheless remain extremely
high when compared with conventional hydrazine thruster. A 400 N hydrazine
thruster approximately has a nozzle diameter [51] while the best performing
radioisotope heated thermionic plasma rocket engine currently requires a heater
chamber of 12 cm to produce the same mass flow conditions as a 1 N hydrazine
thruster.
4.4.2.3.3 Power Consideration
This rocket engine brings considerable energetic benefits by saving a not
negligible amount of power equivalent to the sum of its valves’ power. During
operation it is self-sufficient and therefore does not require any power input from
the spacecraft and can even supply power to the spacecraft when switched off. A
single rocket engine can provide of electric power and each spacecraft of
the Pleiades HR1 constellation operates four of them. This is equal to of
additional power could be used to supply up to of the spacecraft total power
generation, of its mean power generation and even of the power

176. 134
required by its instruments. additional instruments could thus have been
supported thanks to this new rocket engine.
4.4.2.3.4 Comparative Studies
The performance of this radioisotope heated thermionic plasma rocket exceeds the
ones of conventional rocket engines but it is however bulkier. It can achieve a
wide range of ISPs using different noble gases as propellant and the one achieved
with helium exceeded those of traditional bipropellant rocket engines because
helium has an extremely low molar mass. It however required extremely larger
emitter diameters to generate relatively low amounts of thrust because of the same
reason. A trade-off must therefore be found between achieving high ISPs and
reasonable amounts of thrusts. The use of this new plasma rocket engine will
therefore be recommended for low thrust applications because the size of the
heating chamber is the main obstacle of high thrust generation. Neon came next in
terms of ISP and achieved a specific impulse slightly lower than the one generated
by solid propellant rockets.
4.4.2.3.5 Operation
This radioisotope heated thermionic plasma rocket engine is operated as follows.
First a lifting mechanism puts the radioisotope heat source in contact with the
emitter material then once it is heated up to thermionic temperatures, neutral gas is
injected inside the emitter in order to be ionized. In its current state, the thermionic
electrons produced by the plasma rocket do not possess enough energy to
effectively ionize the neutral gas because of their relatively small mass and of the
space charge effect which limits the thermionic electron current density. An
electric field must therefore be introduced to accelerate thermionic electrons so
that they may generate enough ions through neutral gas ionization because it is the
collisions of the neutral atoms with these ions and the wall that will generate
temperatures exceeding to . The RTG should power this electric field
and the required radioisotope diameter should be increased accordingly. A high
temperature plasma is then produced inside the emitter and generates thrust by
expanding inside the nozzle. Although the emitter material must be heated up
similarly to the catalytic bed of monopropellant rocket engines, it uses a different

177. BUAA Academic Dissertation for Doctoral
135
exothermic process. Monopropellant rockets use chemical reactions to raise the
gas temperature whilst radioisotope heated thermionic plasma rocket engines
accomplish it through gas ionization. The radioisotope heat source needs to remain
in contact with the emitter throughout the operation of the plasma rocket engine
that is switched on and off by disconnecting the radioisotope heat source similarly
to radioisotope heated hollow cathodes. [53]
4.4.2.3.6 Advantages & Disadvantages
The Kabila rocket has several advantages. First it can save a non negligible
amount of power, i.e.: up to 32% of the power required by the instruments of one
of the spacecraft of the Pleiades-HR-1 constellation. Second it can achieve very
high specific impulses exceeding the ones of solid and bipropellant rocket engines,
i.e.: 529 seconds. Its propellant is extremely abundant, i.e.: helium, can be easily
stored and it can also be restarted. Noble gases do not required special thermal
conditioning as opposed to bipropellants and can therefore be stored for longer
periods of time and at no additional energy cost. It also achieved specific impulses
superior to the ones of bi and solid propellant rocket engines but as opposed to the
latter its combustion process can be initiated, interrupted or even operated in pulse
modes as easily as mono and bipropellant rockets, this adding to its precision and
maneuverability.
The Kabila rocket would greatly benefit existing spacecraft by extending their
operation duration and range, lowering their operating cost and facilitating their
routine maneuvers. The rocket can generate great power and fuel savings by on
one hand acting as an independent power source and by removing the need of the
use of power-demanding cryogenic cooling systems to achieve ISPs similar to or
exceeding the ones of liquid propellant systems and by on the other generating far
greater ISPs. This would enable communication satellites, earth observation
satellites and space probes to increase the extent of their payload but also their
operating lives and ranges. This would result in a greater profit generation in the
case of communication and commercial earth observation satellites and in more
versatile and powerful applications for all types of earth observation satellites and
space probes by for instance enabling the latter to operate in regions yet to be

178. 136
explored of deep space where lower solar density as well as ISPs of current space
propulsion systems has so far hindered the operation of current space probes. The
use of an inexpensive and abundant fuel such as helium will further reduce the
operating cost of spacecraft. Communication satellites would therefore be able to
generate further profit for their operators and running earth observation satellites
as well as space probes’ missions would become more affordable. This high ISP
rocket can be more conveniently fired and restarted than equivalent liquid
propellant systems. This would enable communication and earth observation
satellites to periodically fire their thrusters to control their attitude as well as space
probes to adjust their trajectories at a much lower fuel cost than it was previously
possible.
The Kabila rocket also has disadvantages. Its heating chamber like most
radioisotope heated hollow cathodes tends to be extremely voluminous and
potentially hazardous. First the volume occupied by the heating chamber is
currently extremely large but must also include a RTG module and lifting
mechanism in addition to the emitting material and the radioisotope heat source.
Finally radiations emitted by radioisotopes can be very hazardous and could either
harm nearby operators or damage surrounding equipment.These shortcomings
should be tackled because they would increase spacecraft launch cost, limit the
Kabila rocket’s range of operation as well as rendering the launch and retirement
of spacecraft potentially dangerous. Greater propulsion systems’ dimensions
necessarily mean greater launch mass which will directly affect the launch cost.
With its current geometric performance, the Kabila rocket is restraint to a range of
operation of only a few newtons. This range is only suited to low thrust
applications such as earth observation attitude correction thrusters and a far greater
range of operation of several hundred netwons would be required to service orbit
transfer applications used by lower launch cost communication satellites and
automated transfer vehicles. Without appropriate shielding, radioactive materials
would either be dispersed in the atmosphere in the event of a failed launch or
would create a cloud of radioactive space debris when spacecraft are retired
causing potential damage to still operational satellites in earth orbit and
endangering the crew of manned space missions working in the International
Space Station or other national manned space platforms.

179. BUAA Academic Dissertation for Doctoral
139
Conclusion & Further Work
Conclusion
It was demonstrated in this research worked that radioisotopes can indeed be used
as electron sources in space applications. This was accomplished through the
development of the MINAKA and Kabila classes of space propulsion systems.
The MINAKA thruster is a novel type of ion thruster which uses beta minus decay
radioisotopes as electron sources. It uses a cluster of Radioisotope Propulsive
Cells (RPC) to generate micro and even milli-newton thrust levels of the same
order of magnitude as conventional ion and hall thrusters. RPCs are composed of
Radioisotope Electron Sources (RES) and an Accelerator Grid. Each RES uses a
Radioisotope Source, an Electron Velocity Modulator (EVM) and a Radioisotope
Thermoelectric Generator (RTG). The EVM decelerates radioisotope electrons up
to an optimal ionization energy while the RTG uses the decay heat of the
radioisotope source to simultaneously power the EVM and the Accelerator Grid
making the MINAKA thruster completely self-powered and enabling it to even
generate a not negligible amount of electricity for its spacecraft. Methods were
introduced to confine the plasma and achieve precise thrust vectors. The ionization
geometry and RTGs conversion efficiency were found to have a limited influence
on the thruster’s performances whilst the degree of ionization and radioisotope
density appeared to have a much greater impact on them. The MINAKA thruster
requires an appropriate shielding because it may emit dangerous radiations and its
applications depend on its radioisotopes’ half life. Although it brought certain
power savings and geometric advantages it was found more hazardous to operate
than conventional thrusters. The RESs of the MINAKA thruster could
subsequently used to develop additional space propulsion systems.
The utility of radioisotope properties was maximized by using their decay heat to
generate electron currents. This was accomplished through the development of a
power-free radioisotope heated thermionic electron source technology. This
technology was subsequently used to develop the Kabila cathode and class of
space propulsion systems. Thermionic emissions were successfully initiated using
Strontium-90, Plutonium-238 and Curium-244 and a wide range of electron

180. Chapter 4 Radioisotope Heated Thermionic Electron Source
140
current densities were achieved using different insert materials. A thermal
reductive layer was used to more precisely modulate electron emission current
densities. The heater supply of the Kabila cathode power configuration was
replaced with a RTG supply and the mode of operation of the device was modified
because radioisotope heat sources cannot be switched off. The Kabila cathode was
benchmarked against two ion thruster configurations and it was found that large
size thrusters achieved better geometric performances whilst small and medium
size ion thrusters achieved better energetic performances. A maximum overall
power saving of 3% was achieved. This hollow cathode has some advantages and
several disadvantages. It is scalable and can save a not negligible amount of power
but it is heavier, more voluminous and hazardous than conventional hollow
cathodes. The Kabila rocket is a radioisotope heated thermionic plasma rocket
engine which was successfully developed by using a suitable radioisotope,
Curium-244, to initiate the thermionic emissions that would through ionization
increase the temperature of its propellant. The Kabila rocket also used a thermal
reductive layer and was benchmarked against a 1 N Hydrazine Thruster
configuration operated on one of the Pleiades-HR-1 constellation spacecraft and a
maximal specific impulse and power saving of respectively 529 seconds and 32%
were achieved with helium as propellant. Its advantages were its power saving
capability, high specific impulses and simultaneous ease of storage and restart. It
can however be extremely voluminous and potentially hazardous.
In conclusion this feasibility study led to the development of two novel classes of
space propulsion systems gathered under the general term Radion thrusters, i.e.:
Radioisotope based ion thrusters.

181. BUAA Academic Dissertation for Doctoral
141
Further Work
The development of Radion thrusters has opened a total new and extensive field of
research and numerous directions are now opened for investigation. Further work
could try to improve the performance of Radion thrusters, determine the
performance characteristics of other radioisotopes, develop additional applications
for the two power-free electron source technology that are the RES and Kabila
cathode and investigate the physics of its operation in order to ultimately validate
all Radion thrusters as viable electric space propulsion alternatives. Initial focus
could be given to the reduction of the scale of the Kabila rocket and to the
investigation of the full range of space and terrestrial applications of RESs and
Kabila cathodes.

183. BUAA Academic Dissertation for Doctoral
143
5 APPENDICES
Appendix A: Oopic Programming Script used to simulated the
ionization process inside the discharge chamber of the Minaka
thruster
MinakaWithElectronsConfinement
{
Simulation of the neutral ionization inside the Minaka propulsive cell with an
electrostatic confinement
}
// Specifies all the variables used during the simulation
Variables
{
Jmax=100 // number of grid in the x1 direction per metre
Kmax=100 // number of grid in the x2 direction per metre
RP=1 // Relative Permittivity of Material
ld=0.01 //discharge chamber lenght (m)
Irad= 1e-5*(ld*100)^2*1/ld // Radioisotope electron current [A] adjusted to take
the x3 symmetric axis [1 (m)] into consideration
EVel=3.25e6 // electron drift velocity [m/s]
NeuPres=6e-5 // neutral gas pressure [Torr]
MacPar=1e3 // Macroparticles density
}

184. Chapter 5 Appendices
144
// Specifies all the elements used during the simulation
Region
{
// Specifies the parameters of the grid
Grid
{
J=Jmax //Number of cells in the x1 direction
K=Kmax //Number of cells in the x2 direction
x1s=0 //Lower coordinate in the x1 direction
x1f=ld //higher coordinate in the x1 direction
x2s=0 //Lower coordinate in the x2 direction
x2f=ld //Higher coordinate in the x2 direction
Geometry=1 // Specifies Cartesian coordinate system
}
// Specifies the Control parameters to be applied
Control
{
ElectrostaticFlag=1 // Specifies electrostatic simulation field solver because
particle motion is non-relativistic
dt=1e-10 // Specifies timestep of the simulation

185. BUAA Academic Dissertation for Doctoral
145
}
// Specifies the Monte Carlo Collision Model
MCC
{
gas = Xe // Specifies the Gas type
pressure = NeuPres // Specifies the Gas pressure in Torr
eSpecies = electron // Specifies the electron species that create ionization
iSpecies = xenon // Specifies the Ion species created from ionization
}
// Specifies ion species paramaters
Species
{
name = xenon // Specifies the name of the species
m = 2.18e-25 // Specifies the species' mass [kg]
q = 1.6e-19 // Specifies the charge [C]
subcycle = 10 //Number of field advances per particle advance
collisionModel=2 // Specifies the collision model as the one of an
electron
}

186. Chapter 5 Appendices
146
// Specifies secondary electron species paramaters
Species
{
name = secelectrons // Specifies the name of the species
m = 9.11E-31 // Specifies the species' mass [kg]
q = -1.6e-19 // Specifies the charge [C]
collisionModel=1 // Specifies the collision model as the one of an electron
}
// Specifies electron species paramaters
Species
{
name=electron // Specifies electrons as the species used
collisionModel=1 // Specifies the collision model as the one of an electron
}
// Specifies all electron emission boundaries
BeamEmitter

187. BUAA Academic Dissertation for Doctoral
147
{
j1=0 // Specifies x1 index for first Beam Emitter endpoint
k1=0 // Specifies x2 index for Beam Emitter boundary endpoint
j2=0 // Specifies x1 index for second Beam Emitter endpoint
k2=Kmax // Specifies x2 index for second Beam Emitter endpoint
normal=1 // Specifies the orientation of the Beam Emitter
speciesName=electron // Specifies the name of the emitted species
I=Irad // Specifies the current [A]
np2c=MacPar // Specifies the number of electrons per macroparticles
v1drift=EVel // Specifies the drift Velocity [m/s]
Secondary
{
secondary = 0.5
secSpecies = secelectrons
iSpecies = xenon
}
}
BeamEmitter
{

188. Chapter 5 Appendices
148
j1=0 // Specifies x1 index for first boundary endpoint
k1=0 // Specifies x2 index for first boundary endpoint
j2=Jmax // Specifies x1 index for second boundary endpoint
k2=0 // Specifies x2 index for second boundary endpoint
name=lower // Specifies the name of the boundary
normal=1 // Specifies the orientation of the boundary
speciesName=electron // Specifies the name of the emitted species
I=Irad // Specifies the current [A]
np2c=MacPar // Specifies the number of electrons per macroparticles
v2drift=EVel // Specifies the drift Velocity [m/s]
Secondary
{
secondary = 0.5
secSpecies = secelectrons
iSpecies = xenon
}
}
BeamEmitter
{
j1=0 // Specifies x1 index for first boundary endpoint

189. BUAA Academic Dissertation for Doctoral
149
k1=Kmax // Specifies x2 index for first boundary endpoint
j2=Jmax // Specifies x1 index for second boundary endpoint
k2=Kmax // Specifies x2 index for second boundary endpoint
name=upper // Specifies the name of the boundary
normal=-1 // Specifies the orientation of the boundary
speciesName=electron // Specifies the name of the emitted species
I=Irad // Specifies the current [A]
np2c=MacPar // Specifies the number of electrons per macroparticles
v2drift=EVel // Specifies the drift Velocity [m/s]
Secondary
{
secondary = 0.5
secSpecies = secelectrons
iSpecies = xenon
}
}
BeamEmitter
{
j1=Jmax // Specifies x1 index for first boundary endpoint

190. Chapter 5 Appendices
150
k1=0 // Specifies x2 index for first boundary endpoint
j2=Jmax // Specifies x1 index for second boundary endpoint
k2=Kmax // Specifies x2 index for second boundary endpoint
name=right // Specifies the name of the boundary
normal=-1 // Specifies the orientation of the boundary
speciesName=electron // Specifies the name of the emitted species
I=Irad // Specifies the current [A]
np2c=MacPar // Specifies the number of electrons per macroparticles
v1drift=EVel // Specifies the drift Velocity [m/s]
Secondary
{
secondary = 0.5
secSpecies = secelectrons
iSpecies = xenon
}
}
// Specifies all conducting boundaries
Conductor
{
reflection= 1 //Specifies that all particles will be fully reflected by the Beam
Emitter

191. BUAA Academic Dissertation for Doctoral
151
j1=0 // Specifies x1 index for first Beam Emitter endpoint
k1=0 // Specifies x2 index for Beam Emitter boundary endpoint
j2=0 // Specifies x1 index for second Beam Emitter endpoint
k2=Kmax // Specifies x2 index for second Beam Emitter endpoint
normal=1 // Specifies the orientation of the Beam Emitter
}
Conductor
{
reflection= 1 //Specifies that all particles will be fully reflected by the Beam
Emitter
j1=0 // Specifies x1 index for first boundary endpoint
k1=0 // Specifies x2 index for first boundary endpoint
j2=Jmax // Specifies x1 index for second boundary endpoint
k2=0 // Specifies x2 index for second boundary endpoint
name=lower // Specifies the name of the boundary
normal=1 // Specifies the orientation of the boundary
}
Conductor
{
reflection= 1 //Specifies that all particles will be fully reflected by the Beam
Emitter

192. Chapter 5 Appendices
152
j1=0 // Specifies x1 index for first boundary endpoint
k1=Kmax // Specifies x2 index for first boundary endpoint
j2=Jmax // Specifies x1 index for second boundary endpoint
k2=Kmax // Specifies x2 index for second boundary endpoint
name=upper // Specifies the name of the boundary
normal=-1 // Specifies the orientation of the boundary
}
Conductor
{
reflection= 1 //Specifies that all particles will be fully reflected by the Beam
Emitter
j1=Jmax // Specifies x1 index for first boundary endpoint
k1=0 // Specifies x2 index for first boundary endpoint
j2=Jmax // Specifies x1 index for second boundary endpoint
k2=Kmax // Specifies x2 index for second boundary endpoint
name=right // Specifies the name of the boundary
normal=-1 // Specifies the orientation of the boundary
}
}

193. BUAA Academic Dissertation for Doctoral
153
MinakaWithoutElectronsConfinement
{
Simulation of the neutral ionization inside the Minaka propulsive cell without an
electrostatic confinement
}
Variables
{
Jmax=100 // number of grid in the x1 direction per metre
Kmax=100 // number of grid in the x2 direction per metre
RP=1 // Relative Permittivity of Material
ld=0.01 //discharge chamber lenght (m)
Irad= 1e-5*(ld*100)^2*1/ld // Radioisotope electron current [A] adjusted to take
the x3 symmetric axis [1 (m)] into consideration
EVel=3.25e6 // electron drift velocity [m/s]
NeuPres=6e-5 // neutral gas pressure [Torr]
MacPar=1e3 // Macroparticles density
}
// Specifies all the elements used during the simulation
Region
{

194. Chapter 5 Appendices
154
// Specifies the parameters of the grid
Grid
{
J=Jmax //Number of cells in the x1 direction
K=Kmax //Number of cells in the x2 direction
x1s=0 //Lower coordinate in the x1 direction
x1f=ld //higher coordinate in the x1 direction
x2s=0 //Lower coordinate in the x2 direction
x2f=ld //Higher coordinate in the x2 direction
Geometry=1 // Specifies Cartesian coordinate system
}
// Specifies the Control parameters to be applied
Control
{
ElectrostaticFlag=1 // Specifies electrostatic simulation field solver because
particle motion is non-relativistic
dt=1e-10 // Specifies timestep of the simulation
}

195. BUAA Academic Dissertation for Doctoral
155
// Specifies the Monte Carlo Collision Model
MCC
{
gas = Xe // Specifies the Gas type
pressure = NeuPres // Specifies the Gas pressure in Torr
eSpecies = electron // Specifies the electron species that create ionization
iSpecies = xenon // Specifies the Ion species created from ionization
}
// Specifies ion species paramaters
Species
{
name = xenon // Specifies the name of the species
m = 2.18e-25 // Specifies the species' mass [kg]
q = 1.6e-19 // Specifies the charge [C]
subcycle = 10 //Number of field advances per particle advance
collisionModel=2 // Specifies the collision model as the one of an
electron
}
// Specifies secondary electron species paramaters
Species

196. Chapter 5 Appendices
156
{
name = secelectrons // Specifies the name of the species
m = 9.11E-31 // Specifies the species' mass [kg]
q = -1.6e-19 // Specifies the charge [C]
collisionModel=1 // Specifies the collision model as the one of an electron
}
// Specifies electron species paramaters
Species
{
name=electron // Specifies electrons as the species used
collisionModel=1 // Specifies the collision model as the one of an electron
}
EmitPort
{
//reflection=1
j1=0 // Specifies x1 index for first Beam Emitter endpoint
k1=0 // Specifies x2 index for Beam Emitter boundary endpoint

197. BUAA Academic Dissertation for Doctoral
157
j2=0 // Specifies x1 index for second Beam Emitter endpoint
k2=Kmax // Specifies x2 index for second Beam Emitter endpoint
normal=1 // Specifies the orientation of the Beam Emitter
speciesName=electron // Specifies the name of the emitted species
I=Irad // Specifies the current [A]
np2c=MacPar // Specifies the number of electrons per macroparticles
v1drift=EVel // Specifies the drift Velocity [m/s]
Secondary
{
secondary = 0.5
secSpecies = secelectrons
iSpecies = xenon
}
}
EmitPort
{
//reflection=1
j1=0 // Specifies x1 index for first boundary endpoint
k1=0 // Specifies x2 index for first boundary endpoint
j2=Jmax // Specifies x1 index for second boundary endpoint
k2=0 // Specifies x2 index for second boundary endpoint
name=lower // Specifies the name of the boundary

198. Chapter 5 Appendices
158
normal=1 // Specifies the orientation of the boundary
speciesName=electron // Specifies the name of the emitted species
I=Irad // Specifies the current [A]
np2c=MacPar // Specifies the number of electrons per macroparticles
v2drift=EVel // Specifies the drift Velocity [m/s]
Secondary
{
secondary = 0.5
secSpecies = secelectrons
iSpecies = xenon
}
}
EmitPort
{
//reflection=1
j1=0 // Specifies x1 index for first boundary endpoint
k1=Kmax // Specifies x2 index for first boundary endpoint
j2=Jmax // Specifies x1 index for second boundary endpoint
k2=Kmax // Specifies x2 index for second boundary endpoint
name=upper // Specifies the name of the boundary
normal=-1 // Specifies the orientation of the boundary

199. BUAA Academic Dissertation for Doctoral
159
speciesName=electron // Specifies the name of the emitted species
I=Irad // Specifies the current [A]
np2c=MacPar // Specifies the number of electrons per macroparticles
v2drift=EVel // Specifies the drift Velocity [m/s]
Secondary
{
secondary = 0.5
secSpecies = secelectrons
iSpecies = xenon
}
}
EmitPort
{
//reflection=1
j1=Jmax // Specifies x1 index for first boundary endpoint
k1=0 // Specifies x2 index for first boundary endpoint
j2=Jmax // Specifies x1 index for second boundary endpoint
k2=Kmax // Specifies x2 index for second boundary endpoint
name=right // Specifies the name of the boundary
normal=-1 // Specifies the orientation of the boundary

200. Chapter 5 Appendices
160
speciesName=electron // Specifies the name of the emitted species
I=Irad // Specifies the current [A]
np2c=MacPar // Specifies the number of electrons per macroparticles
v1drift=EVel // Specifies the drift Velocity [m/s]
Secondary
{
secondary = 0.5
secSpecies = secelectrons
iSpecies = xenon
}
}
}

201. BUAA Academic Dissertation for Doctoral
161
Appendix B: Numerical Data collected to plot the degree of
ionization and thrust density performance curves of the Minaka
Thruster
5.1.1 Neutral Gas Temperature = 300 C
Diagram B1 Ion count plot for Tn=300C Ld=1cm, macro-to-real particle=1e3 and x3=1
m
Diagram B2 Ion count plot for Tn=300C Ld=2cm, macro-to-real particle=1e3 and x3=1
m

202. Chapter 5 Appendices
162
Diagram B3 Ion count plot for Tn=300C Ld=3cm, macro-to-real particle=1e4 and x3=1
m
Diagram B4 Ion count plot for Tn=300C Ld=4cm, macro-to-real particle=1e5 and x3=1
m

203. BUAA Academic Dissertation for Doctoral
163
Diagram B5 Ion count plot for Tn=300C Ld=5cm, macro-to-real particle=1e5 and x3=1
m
Diagram B6 Ion count plot for Tn=300C Ld=6cm, macro-to-real particle=1e5 and x3=1
m

204. Chapter 5 Appendices
164
Diagram B7 Ion count plot for Tn=300C Ld=7cm, macro-to-real particle=1e5 and x3=1
m
Diagram B8 Ion count plot for Tn=300C Ld=8cm, macro-to-real particle=1e5 and x3=1
m

205. BUAA Academic Dissertation for Doctoral
165
Diagram B9 Ion count plot for Tn=300C Ld=9cm, macro-to-real particle=1e5 and x3=1
m
Diagram B10 Ion count plot for Tn=300C Ld=10cm, macro-to-real particle=1e5 and
x3=1 m

206. Chapter 5 Appendices
166
5.1.2 Neutral Gas Temperature= 500C
Diagram B11 Ion count plot for Tn=500C Ld=1cm, macro-to-real particle=1e3 and x3=1
m
Diagram B12 Ion count plot for Tn=500C Ld=2cm, macro-to-real particle=1e3 and x3=1
m

207. BUAA Academic Dissertation for Doctoral
167
Diagram B13 Ion count plot for Tn=500C Ld=3cm, macro-to-real particle=1e4 and x3=1
m
Diagram B14 Ion count plot for Tn=500C Ld=4cm, macro-to-real particle=1e5 and x3=1
m

208. Chapter 5 Appendices
168
Diagram B15 Ion count plot for Tn=500C Ld=5cm, macro-to-real particle=1e5 and x3=1
m
Diagram B16 Ion count plot for Tn=500C Ld=6cm, macro-to-real particle=1e5 and x3=1
m

209. BUAA Academic Dissertation for Doctoral
169
Diagram B17 Ion count plot for Tn=500C Ld=7cm, macro-to-real particle=1e5 and x3=1
m
Diagram B18 Ion count plot for Tn=500C Ld=8cm, macro-to-real particle=1e6 and x3=1
m

210. Chapter 5 Appendices
170
Diagram B19 Ion count plot for Tn=500C Ld=9cm, macro-to-real particle=1e6 and x3=1
m
Diagram B20 Ion count plot for Tn=500C Ld=10cm, macro-to-real particle=1e6 and
x3=1 m

211. BUAA Academic Dissertation for Doctoral
171
5.1.3 Increasing Pressure from 1e-7 to 1e-1 [Torr]
Diagram B21 Ion count plot for Tn=300C and Pres= 1e-1 [Torr] Ld=1cm, macro-to-real
particle=1e3 and x3=1 m
Diagram B22 Ion count plot for Tn=300C and Pres= 1e-2 [Torr] Ld=1cm, macro-to-real
particle=1e3 and x3=1 m

212. Chapter 5 Appendices
172
Diagram B23 Ion count plot for Tn=300C and Pres= 1e-3 [Torr] Ld=1cm, macro-to-real
particle=1e3 and x3=1 m
Diagram B24 Ion count plot for Tn=300C and Pres= 1e-4 [Torr] Ld=1cm, macro-to-real
particle=1e3 and x3=1 m

213. BUAA Academic Dissertation for Doctoral
173
Diagram B25 Ion count plot for Tn=300C and Pres= 1e-5 [Torr] Ld=1cm, macro-to-real
particle=1e3 and x3=1 m
Diagram B26 Ion count plot for Tn=300C and Pres= 1e-6 [Torr] Ld=1cm, macro-to-real
particle=1e3 and x3=1 m

214. Chapter 5 Appendices
174
Diagram B27 Ion count plot for Tn=300C and Pres= 1e-7 [Torr] Ld=1cm, macro-to-real
particle=1e2 and x3=1 m

215. BUAA Academic Dissertation for Doctoral
175
References
[1] G. P. Sutton, O. Biblarz, Rocket propulsion elements : an introduction to the
engineering of rockets[G], 7 ed., JOHN WILEY & SONS, Canada, 2001.
[2] D.M. Goebel, I. Katz, fundamentals of Electric Propulsion: Ion and Hall
Thrusters [G], JPL SPACE SCIENCE AND TECHNOLOGY SERIES, (2008).
[3] K. Kuriki, K. Uematsu, S. Morimoto, MPD arcjet performance with various
propellants[A], in: 16th International Electric Propulsion Conference[C],
American Institute of Aeronautics and Astronautics, 1982.
[4] C. Leonard, L. Benjamin, O. Chris, B. Maxwell, M. Greg, I. Andrew, C. Mark,
G. Tim, S. Jared, D. Franklin Chang, D. Chang, B. Edgar, VASIMR Performance
Results[A], in: 46th AIAA/ASME/SAE/ASEE Joint Propulsion Conference &
Exhibit[C], American Institute of Aeronautics and Astronautics, 2010.
[5] K. Boyer, Nuclear rockets[A], in: 4th Annual Meeting and Technical
Display[C], American Institute of Aeronautics and Astronautics, 1967.
[6] R. Mcclellan, Gaseous nuclear fission rockets[A], in: 18th Joint Propulsion
Conference[C], American Institute of Aeronautics and Astronautics, 1982.
[7] L. Robert, Fundamental Analysis of Radioisotope Propulsion[G], in: Space
2006, American Institute of Aeronautics and Astronautics, 2006.
[8] G.J.M. Hagelaar, D.B. Mihailova, J. Van Dijk, Analytical model of a
longitudinal hollow cathode discharge [J], Journal of Physics D: Applied Physics,
43 (2010).
[9] H. Chuaqui, M. Favre, L. Soto, E.S. Wyndham, High current electron beam
generation in a vacuum transient hollow cathode discharge [J], IEEE Transactions
on Plasma Science, 21 (1993) 778-783.
[10] I. Katz, I.G. Mikellides, D.M. Goebel, J.E. Polk, Insert heating and ignition in
inert-gas hollow cathodes [J], IEEE Transactions on Plasma Science, 36 (2008)
2199-2206.

216. References
176
[11] A. Sengupta, Magnetic confinement in a ring-cusp ion thruster discharge
plasma [J], Journal of Applied Physics, 105 (2009).
[12] Z. Lingwei, L. Yu, L. Juan, G. Zuo, J. Haocheng, W. Haixing, T. Haibin,
Numerical Simulation of Characteristics of CEX Ions in Ion Thruster Optical
System [J], Chinese Journal of Aeronautics, 23 (2010) 15-21.
[13] L. Popelier, A. Aanesland, S. Mazouffre, P. Chabert, Extraction and
acceleration of ions from an ion-ion plasma - Application to space propulsion [A],
in: 5th International Conference on Recent Advances in Space Technologies[C],
RAST 2011, June 9, 2011 - June 11, 2011, IEEE Computer Society, Istanbul,
Turkey, 2011, pp. 708-711.
[14] R. McLaren, M. Ragheb, Nuclear propulsion choices for space exploration[A],
in: 1st International Nuclear and Renewable Energy Conference, INREC'10[C],
IEEE Computer Society, Amman, Jordan, 2010.
[15] G. Miskolczy, D.P. Lieb, Radioisotope thermionic converters for space
applications[A], in: Proceedings of the 25th Intersociety Energy Conversion
Engineering Conference - IECEC '90[C], August 12, 1990 - August 17, 1990, Publ
by IEEE, Reno, NV, USA, 1990, pp. 222-226.
[16] H.R. Williams, R.M. Ambrosi, N.P. Bannister, A Mars hopping vehicle
propelled by a radioisotope thermal rocket: Thermofluid design and materials
selection[A], Proceedings of the Royal Society A: Mathematical, Physical and
Engineering Sciences[C], 467 (2011) 1290-1309.
[17] G.L. Bennett, R.J. Hemler, A. Schock, Status report on the U.S. space nuclear
program [J], Acta Astronautica, 38 (1996) 551-560.
[18] G.R. Schmidt, D.H. Manzella, H. Kamhawi, T. Kremic, S.R. Oleson, J.W.
Dankanich, L.A. Dudzinski, Radioisotope electric propulsion (REP): A near-term
approach to nuclear propulsion [J], Acta Astronautica, 66 (2010) 501-507.
[19] L.S. Mason, Realistic specific power expectations for advanced radioisotope
power systems [J], Journal of Propulsion and Power, 23 (2007) 1075-1079.

217. BUAA Academic Dissertation for Doctoral
177
[20] E. Mainardi, The MAUS nuclear space reactor with ion propulsion system [J],
Nuclear Instruments and Methods in Physics Research, Section A: Accelerators,
Spectrometers, Detectors and Associated Equipment, 561 (2006) 331-335.
[21] A.N. Grubisic, S.B. Gabriel, Thrust production mechanisms in hollow
cathode microthrusters [A], in: 2010 IEEE Aerospace Conference[C], March 6,
2010 - March 13, 2010, IEEE Computer Society, Big Sky, MT, United states,
2010, pp. Aerospace and Electronics Systems Society.
[22] Y. Watanabe, J. Appelbaum, I. Maya, Stability of MHD plasmas ionized by
nuclear fragments [A], in: Proceedings of the 26th Intersociety Energy
Conversion Engineering Conference [C]- IECEC '91, August 4, 1991 - August 9,
1991, Publ by IEEE, Boston, MA, USA, 1991, pp. 87-92.
[23] C. Bruno, M. Rosa-Clot, Curium-244 alpha emission for a nano- and micro-
Newton thruster [J], Acta Astronautica, 38 (1996) 231-234.
[24] A. Sanchez-Torres, Radioisotope Power Systems for Space Applications[G],
in: P.N. Singh (Ed.) Radioisotopes - Applications in Physical Sciences, InTech,
2011.
[25] L.S. Mason, Realistic specific power expectations for advanced radioisotope
power systems[J], Journal of Propulsion and Power, 23 (2007) 1075-1079.
[26] B.C. Blanke, J.H. Birden, K.C. Jordan, E.L. Murphy, NUCLEAR
BATTERY-THERMOCOUPLE TYPE SUMMARY REPORT[R], in: AEC
Research and Development REPORT, MONSANTO RESEARCH
CORPORATION, 1962.
[27] External Radiation Protection - Shielding - X and Gamma Radiation, in:
D.o.E. Safety (Ed.) Radiation Protection Training Manual & Study Guide,
University of Maryland · Division of Administration & Finance · Maryland, 1994.
[28] H.J. Bicehouse, Module 4 Basics of Radiation Protection [PDF Document].
Retrieved from Lecture Notes Online Website:
http://www.rinsc.ri.gov/healthphysics/

218. References
178
[29] Gamma Ray Dose Constants, in: I. Integrated Environmental Management
(Ed.), Integrated Environmental Management, Inc. Available from:
http://www.iem-inc.com/information/tools/gamma-ray-dose-constants.
[30] J.H. Hubbell, S.M. Seltzer, Radiation Research 136, 147[DB/OL], in,
National Institute of Standards and Technology, Gaithersburg, MD, 1993.
[31] American National Standard for Gamma-Ray Attenuation Coefficients and
Buildup Factors for Engineering Materials - ANSI/ANS-6.4.3-1991[DB/OL], in,
1991.
[32] J.G. J. Magill, Nuclear Energetics & Radioactivity and Nuclear Reactions [G],
in: RADIOACTIVITY RADIONUCLIDES RADIATION, Springer, 2005.
[33] W. Lotz, Electron-Impact Ionization Cross-Sections and Ionization Rate
Coefficients for Atoms and Ions[J], Astrophysical Journal Supplement, 14 (1967).
[34] L.F. Berzak, S.E. Dorfman, S.P. Smith, Paschen's Law in Air and Nobles
Gases (2006). Unpublished manuscript. Retrieved from: http://www-
eng.lbl.gov/~shuman/XENON/REFERENCES&OTHER_MISC/paschen_report.p
df
[35] N. Zouache, A. Lefort, Electrical breakdown of small gaps in vacuum[A],
IEEE Transactions on Dielectrics and Electrical Insulation[C], 4 (1997) 358-364.
[36] J. Polk, R. Kakuda, J. Anderson, J. Brophy, V. Rawlin, M. Patterson, J. Sovey,
J. Hamley, Validation of the NSTAR ion propulsion system on the Deep Space
One mission - Overview and initial results[A], in: 35th Joint Propulsion
Conference and Exhibit[C], American Institute of Aeronautics and Astronautics,
1999.
[37] R.E. Wirz, DISCHARGE PLASMA PROCESSES OF RING-CUSP ION
THRUSTERS[D], in, CALIFORNIA INSTITUTE OF TECHNOLOGY, Pasadena,
California, 2005, pp. 239.
[38] [cited 2014 May 3rd]; Available from:
http://physics.nist.gov/PhysRefData/XrayMassCoef/ElemTab/z82.html

219. BUAA Academic Dissertation for Doctoral
179
[39] [cited 2014 May 3rd]; Available from:
http://physics.nist.gov/PhysRefData/XrayMassCoef/ElemTab/z82.html
[40] G.L. Kulcinski, Lecture 5:Basic Elements of Static RTG’s [PDF document].
Retrieved from Lecture Notes Online Website:
http://fti.neep.wisc.edu/neep602/SPRING00/neep602.html
[41] O.W. Richardson, Electron Theory of Matter[J], Philips Magazine, 23 (1912).
[42] A. Ohashi, K. Ueki, Improvement of a 90Sr radioisotope battery[J], Radiation
Physics and Chemistry, 51 (1998) 687.
[43] G.H. Rinehart, Design characteristics and fabrication of radioisotope heat
sources for space missions[J], Progress in Nuclear Energy, 39 (2001) 305-319.
[44] V. Radchenko, B. Andreichikov, H. Wanke, V. Gavrilov, B. Korchuganov, R.
Rieder, M. Ryabinin, T. Economou, Curium-244 alpha-sources for space
research[A], in: 4th Topical Meeting on the Industrial Radiation and Radioisotope
Measurement Applications (IRRMA'99)[C], October 3, 1999 - October 7, 1999,
Elsevier Ltd, Raleigh, NC, USA, 2000, pp. 821-824.
[45] K.K. Jameson, D.M. Goebel, R. Watkins, Hollow Cathode and Thruster
Discharge Chamber Plasma Measurements Using High-Speed Scanning Probes[A],
in: IEPC-2005-269 (Ed.) the 29th International Electric Propulsion Conference[C],
Princeton University, 2005.
[46] D. Herman, A.D. Gallimore, Discharge Chamber Plasma Structure of a 30 cm
NSTAR-type Ion Engine[A], in: 40th AIAA/ASME/SAE/ASEE Joint Propulsion
Conference and Exhibit[C], American Institute of Aeronautics and Astronautics,
2004.
[47] G. Dan, J. Polk, A. Sengupta, Discharge Chamber Performance of the NEXIS
Ion Thruster[A], in: 40th AIAA/ASME/SAE/ASEE Joint Propulsion Conference
and Exhibit[C], American Institute of Aeronautics and Astronautics, 2004.
[48] R. Thomas, P. James, An Overview of the Nuclear Electric Xenon Ion System
(NEXIS) Activity[A], in: 40th AIAA/ASME/SAE/ASEE Joint Propulsion

220. References
180
Conference and Exhibit[C], American Institute of Aeronautics and Astronautics,
2004.
[49] J. Polk, J. Anderson, J. Brophy, V. Rawlin, M. Patterson, J. Sovey, J. Hamley,
An overview of the results from an 8200 hour wear test of the NSTAR ion
thruster[A], in: 35th Joint Propulsion Conference and Exhibit[C], American
Institute of Aeronautics and Astronautics, 1999.
[50] J.R. Brophy, R.Y. Kakuda, J.Polk, al., Ion Propulsion System (NSTAR) DS1
Technology Validation Report[R], in, JPL.
[51] [cited 2014 March 29th]; Available from:
http://cs.astrium.eads.net/sp/spacecraft-propulsion/hydrazine-thrusters/1n-
thruster.html.
[52] [cited 2014 March 29th]; Available from:
https://directory.eoportal.org/web/eoportal/satellite-missions/p/pleiades.
[53] K. Mboyi, J. X. Ren, Y. Liu, Development of a Radioisotope Heated Hollow
Cathode[A], in: 2014 International Conference on Aerospace Engineering[C],
Applied Mechanics and Materials, Moscow (Russia), in press.

221. BUAA Academic Dissertation for Doctoral
181
Acknowledgements
I would like to thank my supervisor, Professor Liu Yu, his research assistant,
Professor Ren Jun Xue, the staff of the International School and of Beihang
University for their academic support, the Chinese Scholarship Council for its
financial assistance and my family, friends and laboratory mates, i.e.: Ali Sarosh,
Muhammad Adnan, Muhammad Shoaib and Dimitar Kamarinchev, for their moral
support and daily guidance.
This research work is dedicated to my mother, Micheline Nathalie Kapinga, after
whom the MINAKA space propulsion class was named and above all else to The
Almighty, God who continuously and consistently granted me the strength,
support, opportunities and inspirations that I required to complete this research
work. Thank you all. Thank You Infinitely, Ô Heavenly Father. All Graces come
from You, All Praises are due to You. Amen.

223. BUAA Academic Dissertation for Doctoral
183
AUTHOR PROFILE
Kalomba Mboyi
The author is a Belgian citizen born in DRC on the 20th
of November 1988. He
graduated from Bath University in the United Kingdom with a MEng in Aerospace
Engineering and is currently pursuing a PhD in Aerospace Propulsion Theory and
Engineering at Beihang University. His research interests are advanced space
propulsion systems and radioisotope based propulsion systems. He developed his
PhD research period the Radion thruster concept to which the MINAKA and
Kabila classes of space propulsion systems belong.
Research Outcomes
ACCEPTED SCI JOURNAL PAPER:
1) K. Mboyi, J. X. Ren, Y. Liu, Development of the Kabila Rocket, a
Radioisotope Heated Thermionic Plasma Rocket, Chinese Journal of
Aeronautics[J], in press, 2014.
PUBLISHED EI/CONFERENCE:
2) K. Mboyi, J. X. Ren, Y. Liu, Development of a Radioisotope Heated Hollow
Cathode[A], in: 2014 International Conference on Aerospace Engineering[C],
Applied Mechanics and Materials, Moscow (Russia), in press.