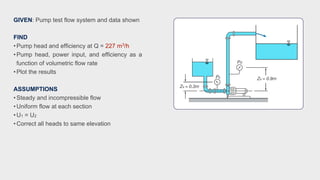
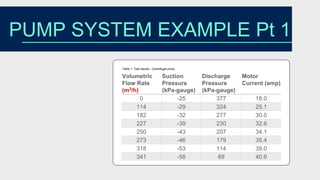
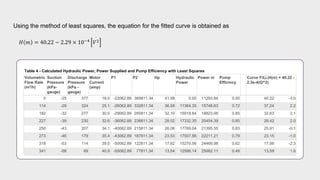
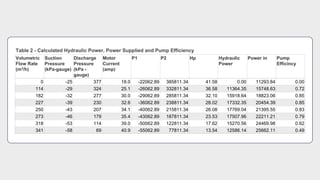
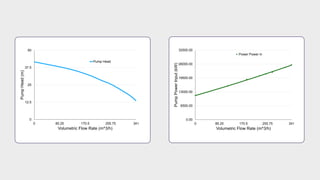
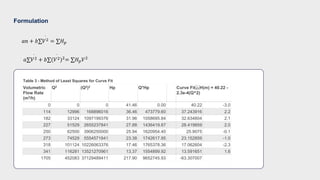
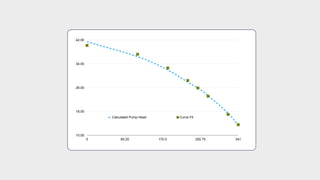
The document summarizes a test of a centrifugal pump. Key details include: - The pump was tested at 1750 rpm with water at 27°C flowing through 150 mm pipes. - Test data on flow rate, suction/discharge pressures, and motor current were provided. - Calculations were shown to determine the pump head and efficiency at 227 m3/h flow. - Additional calculations fitted the performance data to a curve and compared to measurements.

1. KV
WORKED EXAMPLES
{for energy conversion}
Keith Vaugh BEng (AERO) MEng

2. The flow system used to test a centrifugal pump at a
nominal speed of 1750 rpm is shown in the figure. The
liquid water at 27 °C and the suction and discharge pipe
diameters are 150 mm. Data measured during the test
are given in the table. The electric motor is supplied at
460 V, 3-phase, and has a power factor of 0.875 and a
constant efficiency of 90%. Calculate the net head
delivered and the pump efficiency at a volumetric flow
rate of 227m3/h. Plot the pump head, power input and
efficiency as functions of the volumetric flow rate.
PUMP SYSTEM EXAMPLE Pt 1
NOTE - Red text refers to correction made in question

3. Table 1: Test results - Centrifugal pump
Volumetric
Flow Rate
(m3/h)
Suction
Pressure
(kPa-gauge)
Discharge
Pressure
(kPa-gauge)
Motor
Current (amp)
0 -25 377 18.0
114 -29 324 25.1
182 -32 277 30.0
227 -39 230 32.6
250 -43 207 34.1
273 -46 179 35.4
318 -53 114 39.0
341 -58 69 40.9
PUMP SYSTEM EXAMPLE Pt 1

4. GIVEN: Pump test flow system and data shown
FIND
•Pump head and efficiency at Q = 227 m3/h
•Pump head, power input, and efficiency as a
function of volumetric flow rate
•Plot the results
ASSUMPTIONS
•Steady and incompressible flow
•Uniform flow at each section
•U1 = U2
•Correct all heads to same elevation

5. 𝐻𝑝 =
1
𝑔
𝑃
𝜌
+ +𝑔𝑧
𝑑𝑖𝑠𝑐ℎ𝑎𝑟𝑔𝑒
−
𝑃
𝜌
+ 𝑔𝑧
𝑠𝑢𝑐𝑡𝑖𝑜𝑛
=
𝑃2 − 𝑃1
𝜌𝑔
𝐻𝑝 =
𝑃
𝜌𝑔
+
𝑈2
2𝑔
+ 𝑧
𝑑𝑖𝑠𝑐ℎ𝑎𝑟𝑔𝑒
−
𝑃
𝜌𝑔
+
𝑈2
2𝑔
+ 𝑧
𝑠𝑢𝑐𝑡𝑖𝑜𝑛
𝜂𝑝𝑢𝑚𝑝 =
𝑊ℎ
·
𝑊
·
𝑝𝑢𝑚𝑝
=
𝑊ℎ
·
= 𝜌𝑉
·
𝑔𝐻𝑝𝑢𝑚𝑝
𝜔𝑇
𝑊ℎ
·
= 𝜌𝑉
·
𝑔𝐻𝑝𝑢𝑚𝑝
GOVERNING EQUATIONS
Since U1 = U2, the pump head is
where the discharge and suction pressures, corrected to the same elevation,
are designated P2 and P1, respectively

6. 𝐻𝑝 = 28.02𝑚
𝐻𝑝 =
𝑃2 − 𝑃1
𝜌𝑔
=
238.82 − −36.06 × 103
𝑃𝑎
1000𝑘𝑔/𝑚3 × 9.81𝑚/𝑠2
×
𝑘𝑔 ⋅ 𝑚
𝑁 ⋅ 𝑠2
×
𝑁
𝑃𝑎 ⋅ 𝑚2
𝑃2 = 238.82 × 103
𝑃𝑎
𝑃2 = 230 × 103
𝑃𝑎 + 1000𝑘𝑔/𝑚3
× 9.81𝑚/𝑠2
× 0.9𝑚 ×
𝑁 ⋅ 𝑠2
𝑘𝑔 ⋅ 𝑚
×
𝑃𝑎 ⋅ 𝑚2
𝑁
𝑃2 = 𝑃𝑑 + 𝜌𝑔𝑧𝑑
𝑃1 = −39 × 103
𝑃𝑎 + 1000𝑘𝑔/𝑚3
× 9.81𝑚/𝑠2
× 0.3𝑚 ×
𝑁 ⋅ 𝑠2
𝑘𝑔 ⋅ 𝑚
×
𝑃𝑎 ⋅ 𝑚2
𝑁
𝑃1 = 𝑃𝑠 + 𝜌𝑔𝑧𝑠
Correct measured static pressures to the pump centreline
Calculate the pump head
𝑃1 = −36.06 × 103
𝑃𝑎

7. 𝑊ℎ
·
= 17.333 × 103
𝑊
𝑊ℎ
·
= 227
𝑚3
ℎ
×
ℎ
3600𝑠
× 238.82 − −36.06 × 103
𝑃𝑎 ×
𝑁
𝑃𝑎 ⋅ 𝑚2
×
𝐽
𝑁 ⋅ 𝑚
×
𝑤 ⋅ 𝑠
𝐽
𝑊ℎ
·
= 𝜌𝑉
·
𝑔𝐻𝑝𝑢𝑚𝑝 = 𝑉
·
𝑃2 − 𝑃1
Compute the hydraulic power delivered to the fluid
𝜂𝑝 =
𝑊ℎ
·
𝑊
𝑚
· =
17.333 × 103
𝑊
20.4 × 103𝑊
= 0.847 ⟶
𝑃𝑖𝑛 = 20.4 × 103
𝑊
𝑃𝑖𝑛 = 0.9 × 3 × 0.875 × 460𝑉 × 32.6𝐴 ×
𝑊
𝑉𝐴
𝑃𝑖𝑛 = 𝜂 3 𝑃𝐹 𝐸𝐼
Calculate the motor power output (the mechanical power input to the pump) from the electrical information
The corresponding pump efficiency is
𝜂𝑝 = 85%
Convert
𝑚3
ℎ
𝑡𝑜
𝑚3
𝑠

8. Develop and format appropriately an excel worksheet which
calculates the;
•Pump head for each volumetric flow rate provided
•The hydraulic power delivered to the flow for each flow rate
•The power input required to drive the pump at each flow rate
•The pump efficiency at each flow rate
From the resulting dataset, plot the pump head, power input and
efficiency as functions fo volumetric flow-rate and describe what
can be observed or deduced from these results.
PUMP SYSTEM EXAMPLE Pt 2
Table 2 - Given Data
Given Data Value Units
Zs 0.3 m
Zd 0.9 m
RPM 1750 RPM
Temperature 20 deg
Density 998
Gravity 9.81
Efficiency 0.9
Volts 460
Power Factor 0.875

9. Table 2 - Calculated Hydraulic Power, Power Supplied and Pump Efficiency
Volumetric
Flow Rate
(m3/h)
Suction
Pressure
(kPa-gauge)
Discharge
Pressure
(kPa -
gauge)
Motor
Current
(amp)
P1 P2 Hp Hydraulic
Power
Power in Pump
Efficincy
0 -25 377 18.0 -22062.89 385811.34 41.58 0.00 11293.84 0.00
114 -29 324 25.1 -26062.89 332811.34 36.58 11364.35 15748.63 0.72
182 -32 277 30.0 -29062.89 285811.34 32.10 15918.64 18823.06 0.85
227 -39 230 32.6 -36062.89 238811.34 28.02 17332.35 20454.39 0.85
250 -43 207 34.1 -40062.89 215811.34 26.08 17769.04 21395.55 0.83
273 -46 179 35.4 -43062.89 187811.34 23.53 17507.96 22211.21 0.79
318 -53 114 39.0 -50062.89 122811.34 17.62 15270.56 24469.98 0.62
341 -58 69 40.9 -55062.89 77811.34 13.54 12586.14 25662.11 0.49

10. 0
12.5
25
37.5
50
0 85.25 170.5 255.75 341
Pump
Head
(m)
Volumetric Flow Rate (m^3/h)
Pump Head
0.00
6500.00
13000.00
19500.00
26000.00
32500.00
0 85.25 170.5 255.75 341
Pump
Power
Input
(kW)
Volumetric Flow Rate (m^3/h)
Power Power in

11. 0.00
0.23
0.45
0.68
0.90
0 85.25 170.5 255.75 341
Pump
Efficiency
Volumetric Flow Rate (m^3/h)
Pump Efficincy

12. Apply the method of least squares to the calculated pump
performance data obtained above and fit a parabolic curve of
the form 𝐻 = 𝐻𝑜 − 𝐴𝑉2
·
to this data. Include all formulations
and calculations as part of your submission, plot the fitted curve
using excel and compare this with the measured data.
PUMP SYSTEM EXAMPLE Pt 3

13. Formulation
𝑎∑𝑉2
·
+ 𝑏∑(𝑉2)
·
2
= ∑𝐻𝑝𝑉2
𝑎𝑛 + 𝑏∑𝑉2
·
= ∑𝐻𝑝
Table 3 - Method of Least Squares for Curve Fit
Volumetric
Flow Rate
(m3/h)
Q2 (Q2)2 Hp Q*Hp Curve Fit H(m) = 40.22 -
2.3e-4(Q^2)
0 0 0 41.46 0.00 40.22 -3.0
114 12996 168896016 36.46 473779.60 37.243916 2.2
182 33124 1097199376 31.96 1058695.84 32.634604 2.1
227 51529 2655237841 27.88 1436419.87 28.419859 2.0
250 62500 3906250000 25.94 1620954.40 25.9075 -0.1
273 74529 5554571841 23.38 1742617.95 23.152859 -1.0
318 101124 10226063376 17.46 1765378.36 17.062604 -2.3
341 116281 13521270961 13.37 1554899.92 13.591651 1.6
1705 452083 37129489411 217.90 9652745.93 -63.307007

14. Table 4 - Calculated Hydraulic Power, Power Supplied and Pump Efficiency with Least Squares
Volumetric
Flow Rate
(m3/h)
Suction
Pressure
(kPa-
gauge)
Discharge
Pressure
(kPa -
gauge)
Motor
Current
(amp)
P1 P2 Hp Hydraulic
Power
Power in Pump
Efficincy
Curve Fit H(m) = 40.22 -
2.3e-4(Q^2)
0 -25 377 18.0 -22062.89 385811.34 41.58 0.00 11293.84 0.00 40.22 -3.0
114 -29 324 25.1 -26062.89 332811.34 36.58 11364.35 15748.63 0.72 37.24 2.2
182 -32 277 30.0 -29062.89 285811.34 32.10 15918.64 18823.06 0.85 32.63 2.1
227 -39 230 32.6 -36062.89 238811.34 28.02 17332.35 20454.39 0.85 28.42 2.0
250 -43 207 34.1 -40062.89 215811.34 26.08 17769.04 21395.55 0.83 25.91 -0.1
273 -46 179 35.4 -43062.89 187811.34 23.53 17507.96 22211.21 0.79 23.15 -1.0
318 -53 114 39.0 -50062.89 122811.34 17.62 15270.56 24469.98 0.62 17.06 -2.3
341 -58 69 40.9 -55062.89 77811.34 13.54 12586.14 25662.11 0.49 13.59 1.6
Using the method of least squares, the equation for the fitted curve is obtained as
𝐻 𝑚 = 40.22 − 2.29 × 10−4
𝑉2
·

15. 10.00
18.00
26.00
34.00
42.00
0 85.25 170.5 255.75 341
Calculated Pump Head Curve Fit