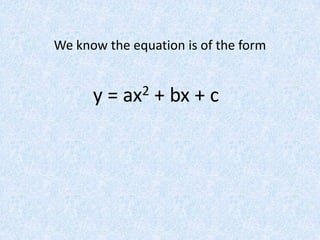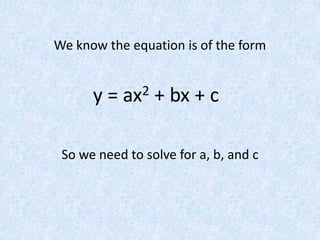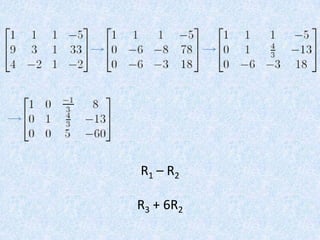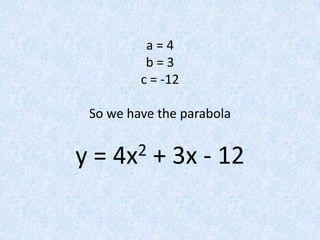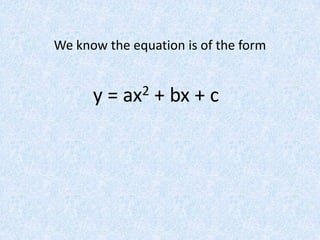
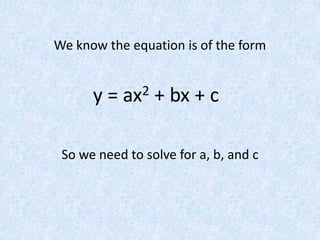
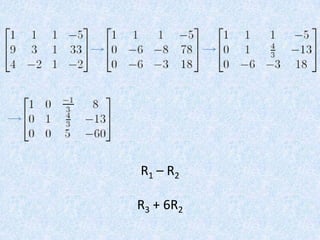
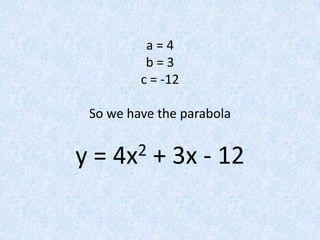
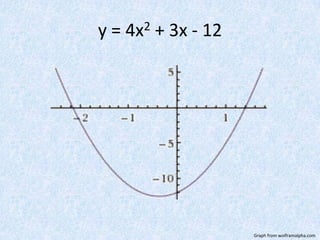
The document finds the equation of a parabola passing through three points (1,-5), (3,33), and (2,-2) by: 1) Writing the general form of a parabolic equation y=ax^2+bx+c and setting up three equations using the three points; 2) Putting the equations into a matrix and row reducing to solve for a, b, and c; 3) Finding the values a=4, b=3, c=-12 and the equation of the parabola to be y=4x^2+3x-12.

1. Find an equation for the parabola thatpasses through the following points:(1,-5)(3,33)(2,-2)

2. We know the equation is of the formy = ax2 + bx + c

3. We know the equation is of the formy = ax2 + bx + cSo we need to solve for a, b, and c

4. Using the point (1,-5), we get the equation-5 = a + b + c

5. Using the point (1,-5), we get the equation-5 = a + b + cUsing the point (3,33), we get the equation33 = 9a + 3b + c

6. Using the point (1,-5), we get the equation-5 = a + b + cUsing the point (3,33), we get the equation33 = 9a + 3b + cUsing the point (-2,-2), we get the equation-2 = 4a - 2b + c

7. We can now put these equations into matrix form where each row is an equation-5 = a + b + c33 = 9a + 3b + c-2 = 4a - 2b + c

8. The first column is the a, the second column is the b, the third column is the c, and the fourth column is y-5 = a + b + c33 = 9a + 3b + c-2 = 4a - 2b + c

9. Now this matrix needs to be converted to reduced row echelon formLet Rn be the nth row,Cm be the mth column

10. R2 – 9R1R3 – 4R1

11. R2 / -6

12. R1 – R2R3 + 6R2

13. R3 / 5

14. R2 – (4/3)R3R1 – (1/3)R3

15. These now represent new equations:a = 4b = 3c = -12

16. a = 4b = 3c = -12So we have the parabolay = 4x2 + 3x - 12

17. y = 4x2 + 3x - 12Graph from wolframalpha.com