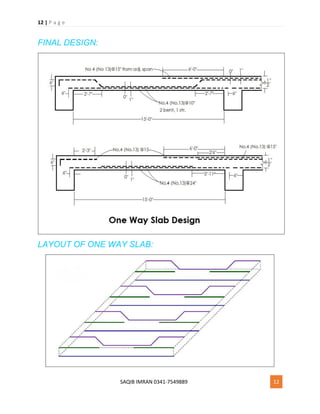
1. The document provides notes on structural engineering topics like slabs, waffle slabs, hidden beams, one-way slabs, and columns. 2. It explains the different types of bars in slabs, the spacing requirements, and how to calculate effective depth. Waffle slabs and hidden beams are described along with their purposes and advantages. 3. The document provides the code specifications for designing a one-way slab and works through an example problem. It also discusses the differences between plinth beams and tie beams.

1. 1 | P a g e
SAQIB IMRAN 0341-7549889 1
Assala mu alykum My Name is saqib imran and I am the
student of b.tech (civil) in sarhad univeristy of
science and technology peshawer.
I have written this notes by different websites and
some by self and prepare it for the student and also
for engineer who work on field to get some knowledge
from it.
I hope you all students may like it.
Remember me in your pray, allah bless me and all of
you friends.
If u have any confusion in this notes contact me on my
gmail id: Saqibimran43@gmail.com
or text me on 0341-7549889.
Saqib imran.

2. 2 | P a g e
SAQIB IMRAN 0341-7549889 2
STRUCTURAL
IMPORTANT NOTES ON SLAB (SPACING, EFFECTIVE DEPTH ETC)
IMPORTANT NOTES ON SLAB:
There are two types of bars present in the slab.
 Main bars
 Distribution bars (bars provided against shrinkage and temperature)
Maximum spacing Between Individual Bars:
1) The maximum diameter of bar used in slab should not exceed 1/8 of the total
thickness of slab.
2) For main bars, maximum spacing is restricted to 3 times effective depth or 300 mm
whichever is smaller.
3) For distribution bars, the maximum spacing is specified as 5 times the effective depth
or 450 mm whichever is smaller.
Hence, diameter of bar, thickness of slab, effective depth and spacing are co-related.
Effective depth = depth of slab – clear cover- half of diameter of bar
Minimum Distance Between Individual Bars:
Minimum Distance Between Individual Bars & main reinforcing bars shall usually be not
less than the greatest of the following:
The following shall apply for spacing of bars:
1) The diameter of the bar if the diameters are equal,
2) The diameter of the larger bar if the diameters are unequal and
3) 5 mm more than the nominal maximum size of coarse aggregate.
Clear cover (Nominal Cover) shall be kept in mind while calculating the above
parameters.
Source: IS-456 (2000)
WAFFLE SLAB – PURPOSE, USES, ADVANTAGES AND DISADVANTAGES
WHAT IS WAFFLE SLAB?
A waffle slab is a type of slab with holes underneath, giving an appearance of waffles. It
is usually used where large spans are required (e.g auditorium) to avoid many columns

3. 3 | P a g e
SAQIB IMRAN 0341-7549889 3
interfering with space. Hence thick slabs spanning between wide beams (to avoid the
beams protruding below for aesthetic reasons) are required.
Since the tensile strength of concrete is mainly satisfied by the steel bar reinforcement,
only the “ribs” containing the reinforcement are kept where the remaining ‘unused’
concrete portion below the neutral axis is removed, to reduce the self-weight of the slab.
This is achieved by placing clay pots or other shapes on the formwork before casting of
the concrete.
PURPOSE OF WAFFLE SLAB:
Waffle slabs provide stiffer and lighter slabs than an equivalent flat slab. The speed of
construction for such slab is faster compared to conventional slab. Relatively lightweight
hence economical. It uses 30% less concrete and 20% less steel than a raft slab. They
provide low floor deflections. It has good finishes and robustness. Fairly slim floor depth
and fire resistant. Excellent vibration control.

4. 4 | P a g e
SAQIB IMRAN 0341-7549889 4
USES AND APPLICATIONS OF WAFFLE SLAB:
It is used where vibration is an issue and where large span slabs are to be constructed
i.e areas having less number of columns. For example airport, hospitals, commercial
and industrial buildings etc & where low slab deflections and high stability are required.
ADVANTAGES OF WAFFLE SLAB:
1. Larger span of slab and floor with less number of columns.
2. load carrying capacity is greater than the other types of slab.
3. Savings on weight and materials.

5. 5 | P a g e
SAQIB IMRAN 0341-7549889 5
4. Good vibration control capacity.
5. Attractive soffit appearance when exposed.
6. Lightweight.
7. Vertical penetrations between ribs are easy.
8. Economical when reusable formwork is used.
9. Fast and speedy construction.
DISADVANTAGES OF WAFFLE SLAB:
1. Require greater floor-to-floor height.
2. Requires special or proprietary formwork which is costly.
3. requires strict supervision and skilled labor.
4. Difficulty in maintenance.
5. Not suitable in highly windy area.
WHAT IS HIDDEN BEAM/CONCEALED BEAM – PURPOSE, ADVANTAGES
& DISADVANTAGES
WHAT IS HIDDEN BEAM?
Hidden beams can be defined as the beams whose depth is equal to the thickness of
the slab. Hidden beams are also known as concealed beam.
Beams normally have a depth larger than the slab it is lifting, however, hidden beams
have the same depth as the slab, but it is reinforced separately from the slab, having
stirrups and longitudinal bars just as a normal beam. Hence they can’t be seen after
fulfilling it with concrete. They are hidden in the slab.

6. 6 | P a g e
SAQIB IMRAN 0341-7549889 6
Hidden beams are generally inserted within the suspended slabs where slab thickness
is considerable. The concept of concealed beam originated from flat slab concept. They
are more applicable in commercial buildings.

7. 7 | P a g e
SAQIB IMRAN 0341-7549889 7
PURPOSE OF HIDDEN BEAMS:
Hidden beams are used for the following purposes
1. To disperse loads on the supporting slab.
2. To break a wide panel of slab to considerable size.
3. To achieve maximum floor height.
4. To clear the way for electromechanical duct work.
5. To improve architectural aesthetic appearance by providing neat and leveled ceiling
surface.

8. 8 | P a g e
SAQIB IMRAN 0341-7549889 8
ADVANTAGES OF HIDDEN BEAM:
1. It saves floor height clearance.
2. It allows if a brickwork needs to be constructed over the slab.
3. It is economical as it saves cost of materials, formwork, and labor.
4. It gives better aesthetic interior appearance.
DISADVANTAGES OF HIDDEN BEAM:
Structurally it creates a spanning problem, as spans for structural support are at right
angle to each other. This means one slab structurally rests over the other.
ONE WAY SLAB DESIGN – HOW TO DESIGN ONE WAY SLAB
WHAT IS ONE WAY SLAB?
When a slab is supported on all four sides and the ratio of long span to short span is
equal or greater than two, it will be considered as one way slab. The load on the slab is
carried by the short span in one direction. However main reinforcement bar and
distribution bar in transverse direction.
Longer span (l)/Shorter span (b) ≥ 2
ACI CODE SPECIFICATIONS FOR ONE WAY SLAB DESIGN:
1. MINIMUM SLAB THICKNESS:
To control deflection, ACI Code 9.5.2.1 specifies minimum thickness values for one-way
solid slabs.
2. SPAN:
According to ACI code 8.7.1 If the slab rests freely on its supports, the span length may
be taken as equal to the clear span plus the depth of the slab but need not exceed the
distance between centers of supports.

9. 9 | P a g e
SAQIB IMRAN 0341-7549889 9
3. BAR SPACING:
The lateral spacing of the flexural bars should not exceed 3 times the thickness h or 18
inch
according to ACI code 7.6.5 The lateral spacing of temperature and shrinkage
reinforcement should not be placed farther apart than 5 times the slab thickness or 18
inch according to ACI code 7.12.2
4. MAXIMUM REINFORCEMENT RATIO:
Reinforcement ratio is the ratio of reinforcement area to gross concrete area based on
total
depth of slab. One-way solid slabs are designed as rectangular sections subjected to
shear and moment. Thus, the maximum reinforcement ratio corresponds to a net tensile
strain in the
reinforcement, €t of 0.004
5. MINIMUM REINFORCEMENT RATIO:
A) FOR TEMPERATURE AND SHRINKAGE
REINFORCEMENT :
According to ACI Code 7.12.2.1
Slabs with Grade 40 or 50 deformed bars –> 0.0020
Slabs with Grade 60 deformed bars –> 0.0018
Slabs where reinforcement with yield strength Exceeding 60000 psi- ->( 0.0018 x
60000/fy)
B) FOR FLEXURAL REINFORCEMENT :
According to ACI Code 10.5.4, the minimum flexural reinforcement is not to be less than
the shrinkage reinforcement, or 0.0018
EXAMPLE PROBLEM:
A reinforced concrete slab is built integrally with its supports and consists of equal span
of 15 ft. The service live load is 100 psf and 4000 psi concrete is specified for use with
steel with a yield stress equal to 60000 psi. Design the slab following the provisions of
the ACI code.

10. 10 | P a g e
SAQIB IMRAN 0341-7549889 10
THICKNESS ESTIMATION:
For being both ends continuous minimum slab thickness = L/28 =(15 x 120)/28= 6.43
in.
Let a trial thickness of 6.50 in.
LOAD CALCULATION:
Consider only a 1 ft width of beam.
Dead load = 150 x (6.50/12)) = 81 psf
Live load = 100 psf
Factored DL and LL ={81+1.2+(100 x 1.6)} =257 psf
DETERMINE MAXIMUM MOMENTS:
Factored moments at critical sections by ACI code :
At interior support : -M=1/9 x 0.257 x 152 = 6.43 k-ft
At midspan : +M=1/14 x 0.257 x 152 = 4.13 k-ft
At exterior support : -M=1/24 x 0.257 x 152 = 2.41 k-ft
Mmax = 6.43 k-ft
=0.85 x 0.85 x 4/60 x 0.003/(0.003+0.004)
= 0.021

11. 11 | P a g e
SAQIB IMRAN 0341-7549889 11
Now,
= 2.64 in
CHECK FOR AVAILABILITY OF THICKNESS:
As ‘d’ is less than the effective depth of (6.50-1.00) = 5.50 in, the thickness of 6.50 in
can be adopted.
REINFORCEMENT CALCULATION:
Let, a = 1 inch
At interior support:
Checking the assumed depth of a by
Similarly at Midspan:
As = (4.13 x 12)/(0.90 x 60 x 5.29) = 0.17 in²
At Exterior support:
As = (2.41 x 12)/(0.90 x 60 x 5.29) = 0.10 in²
MINIMUM REINFORCEMENT:
As = 0.0018 x 12 x 6.50 = 0.14 in²
So we have to provide this amount of reinforcement where As is less than 0.14 in².
SHRINKAGE REINFORCEMENT:
Minimum reinforcement for shrinkage and temperature is
As = 0.0018 x 12 x 6.50 = 0.14 in²

12. 12 | P a g e
SAQIB IMRAN 0341-7549889 12
FINAL DESIGN:
LAYOUT OF ONE WAY SLAB:

13. 13 | P a g e
SAQIB IMRAN 0341-7549889 13
DIFFERENCE BETWEEN PLINTH BEAM AND TIE BEAM
DIFFERENCE BETWEEN PLINTH BEAM AND TIE BEAM:
In this article, I will discuss the difference between plinth beam and tie beam. Before
starting the difference, let me clear one important term which will help you further.
PLINTH LEVEL:
It is the level where the sub-structure ends and superstructure starts. In si simple words
it is the topmost level of ground level. (refer to the below image)
WHAT IS PLINTH BEAM?
The beam which is provided at the plinth level is called plinth beam. In framed structure
plinth beam is the first beam constructed after foundation.
PURPOSE OF PLINTH BEAM:
1. To distribute the load of walls over the foundation.
2. To connect all the columns.
3. To prevent cracks from the foundation to the wall.
4. To avoid differential settlement.

14. 14 | P a g e
SAQIB IMRAN 0341-7549889 14
WHAT IS TIE BEAM?
The beam which connects two or more columns/rafters in a roof/ roof truss or in any
height above floor level is called tie beam. Tie beams are mainly provided in roof truss
and at plinth level. These beams do not convey any floor loads and only act as length
breaker for columns where the floor height is unusually high.
PURPOSE OF TIE BEAM:
1. To carry axial compression.
2. To transfer the rafter’s load to the column.
3. To prevent columns from buckling.
DIFFERENCE BETWEEN PLINTH BEAM AND TIE BEAM:
Now coming to the difference between plinth beam and tie beam. Actually, there is no
difference between them. Tie beam is also a type of plinth beam. When tie beam is
provided at plinth level it is known as plinth beam. That means the only difference is the
height at which they are provided.
Plinth beam is only provided at plinth level but tie beam is provided anywhere above the
plinth level and floor level.
HOW TO CALCULATE BEND DEDUCTION LENGTH OF BAR
HOW TO CALCULATE BEND DEDUCTION LENGTH OF BAR:
When we bend a steel bar, the length of the bar slightly increased due to stretching in
the bending area (refer to below image). The expansion of length depends on the grade
of steel and the degree of bend. The length increases with the increase of bending
degree and decreases with the higher grade steel. (Fe250, Fe450, Fe500)

15. 15 | P a g e
SAQIB IMRAN 0341-7549889 15
In this article, I will discuss how to calculate the bend deduction length for bars.
The formulae for bend deduction are
1. FOR 45° BEND = 1 X D
2. FOR 90° BEND = 2 X D

16. 16 | P a g e
SAQIB IMRAN 0341-7549889 16
3. FOR 135° BEND = 3 X D
4. FOR 180° BEND = 4 X D

17. 17 | P a g e
SAQIB IMRAN 0341-7549889 17
Where d = diameter of the bar.
DESIGN OF COLUMNS AS PER ACI
DESIGN OF COLUMNS AS PER ACI:
1. Maximum and Minimum Reinforcement Ratio:
The minimum reinforcement ratio of 1 % is to be used in tied or spirally reinforced
columns. This minimum reinforcement is needed to safeguard against any bending,
reduce the effect of shrinkage and creep and enhance ductility of columns.
2. Minimum Number of Reinforcing Bars:
Minimum four bars within rectangular or circular sections; or one bar in each corner of
the cross section for other shapes and a minimum of six bars in spirally reinforced
columns should be used.
3. Clear Distance between Reinforcing Bars:
For tied or spirally reinforced columns, clear distance between bars should not be less
than the larger of 150 times bar diameter or 4 cm.
4. Concrete Protection Cover:
The clear concrete cover should not be less than 4 cm for columns not exposed to
weather or in contact with ground. It is essential for protecting the reinforcement from
corrosion or fire hazards.
5. Minimum Cross-Sectional Dimensions:
For practical considerations, column dimensions can be taken as multiples of 5 cm.
6. Lateral Reinforcement:

18. 18 | P a g e
SAQIB IMRAN 0341-7549889 18
Ties are effective in restraining the longitudinal bars from buckling out through the
surface of the column, holding the reinforcement cage together during the construction
process, confining the concrete core and when columns are subjected to horizontal
forces, they serve as shear reinforcement. Spirals, on the other hand, serve in addition
to these benefits in compensating for the strength loss due to spalling of the outside
concrete shell at ultimate column strength.
7. Ties:
For longitudinal bars, 32 mm or smaller, lateral ties 10 mm in diameter should be used.
In our country and in some neighboring countries, ties of 8 mm dia are used for column
construction.
BASIC RULES FOR DESIGN OF COLUMN
BASIC RULES FOR DESIGN OF COLUMN:
The basic rules for designing of columns are listed below:
A. LONGITUDINAL STEEL:
1. The cross-sectional area of longitudinal steel in a column shall not be less than 0.8
and not more than 6% of the gross-sectional area of the column.
In places where bars from a column below have to be lapped with those in the column
to be designed, the maximum percentage of steel should not exceed 4%.
2. The diameter of longitudinal bars should not be less than 12 mm and should not be
more than 50 mm.
3. Round columns and columns having helical binders should have at least bars.
4. The minimum cover of concrete to the outside of longitudinal bars shall be 4 cm or
the diameter of the bar whichever is greater. In case where the maximum dimension of
a column does not exceed 20 cm and the diameter of the longitudinal bars does not
exceed 12 mm, the cover of 2.5 cm may be used.
5. Where it is necessary to splice the longitudinal bars, the bars shall overlap for a
distance of not less than 24 times the diameter of the smallest bar.
6. The spacing of bars measured along the periphery of the column shall not exceed
300 mm.
B. TRANSVERSE REINFORCEMENT:
Transverse steel may be provided either in the form of lateral ties or helical bars (spiral).
1. The minimum diameter of the ties or helical reinforcement shall not less than 1/4th
the diameter of the largest longitudinal bars and in no case less than 5 mm.

19. 19 | P a g e
SAQIB IMRAN 0341-7549889 19
2. The maximum diameter of the ties or helical steel should preferably be not more than
12 mm and 25 mm respectively.
3. The pitch of the ties should not be more than the least of the following
a) Least lateral dimension of the column.
b) 16 times the diameter of the smallest longitudinal bar nearest to the compression
face of the member.
c) 48 times the diameter of the tie.
4. Pitch of the helical reinforcement should not be more than least of the following:
a) 1/6th the diameter of the concrete core.
b) 75mm.
5. The least spacing of the lateral ties may be 150 mm and for spirals, the minimum
pitch shall be 25 mm or three times the diameter of the helical bars whichever is
greater.
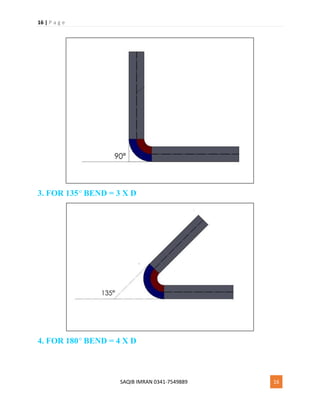
BBS OF LINTEL BEAM – BAR BENDING SCHEDULE OF LINTEL BEAM
BAR BENDING SCHEDULE OF LINTEL BEAM:
In this article, I will discuss how to prepare BBS of RCC Lintel Beam.
1. Calculate Total Length Of Main Bars:
Length of 1 bar = Length of lintel – clear cover for both sides
= 2500 – 2 x 25 [Clear cover for both sides]
=2450 mm

20. 20 | P a g e
SAQIB IMRAN 0341-7549889 20
= 2.4 m.
Length of 4 bars = 2.4 x 4 = 9.6 m
2. Calculate Weight Of Steel For Main Bars:
Weight of steel for 12 mm bar = D²L/162 = 12² x 9.6/162 = 8.53 kg.
3. Calculate No Of Stirrups:
No of stirrups = (Total length of lintel/c/c distance between strriups) + 1
= (2500/150) + 1 = 18
4. Calculate Total Length Of Stirrups:
Inner depth distance = 150 -25 -25 -8 =84 mm
Width distance = 150 – 25 – 25 -8 = 84 mm.
Cutting length of stirrups =(2x Inner deoth diatance) +(2xWidth depth) + Hooks Length –
Bend
Hooks length = 10d
Bend = 2d
We have 2 hooks and 5 bend
So,
Cutting length of stirrups = (2×84) + (2 x84) +2x10x8 -5x2x8 = 418 mm = 0.418 m
Total length of stirrups = 0.418 x 18 = 7.54 m
5. Calculate Weight Of Steel For Stirrups:
Weight of steel for stirrups = D²L/162 = 8² x 7.54/162 = 7.61 kg.
Total weight of steel for lintel = 8.53 + 7.61 = 16.14 kg.
HOW TO CALCULATE HEIGHT OF A BUILDING/TOWER

21. 21 | P a g e
SAQIB IMRAN 0341-7549889 21
HOW TO CALCULATE HEIGHT OF A BUILDING:
Sometimes we may need to find out the height of a building before or after construction.
There are several methods for calculating the height of a building. In this article, I will
use trigonometry method for calculating the height of the building. This is the simplest
method. You can use this method to find out the height of any objects such as tower,
water tank, tree, lighthouse etc,
Required Data:
Distance and angle (as shown in fig).
Given:
Angle = θ = 30º
Distance = d = 3000 feet.

22. 22 | P a g e
SAQIB IMRAN 0341-7549889 22
Procedure:
We know,
Tangent = The ratio of the opposite side to the adjacent side.
Which means tanθ = Opposite side/Adjacent side
here θ = 30º
So tan30º = Opposite side/Adjacent side = x/d = x/3000
x = tan30º x 3000 = 0.577 x 3000 = 1732 feet.
∴ The height of the building is 1732 feet.
DIFFERENCE BETWEEN DEVELOPMENT LENGTH AND LAP LENGTH
DEVELOPMENT LENGTH:
Development length is the length of bar required for transferring the stress into
concrete.
In simple words, the quantity of the rebar length that is actually required to be
embedded into the concrete to achieve the desired bond strength between concrete and
steel by producing required stress for the steel in that area.
The formula for development is given below:
Development length (Ld) = d x σs/τbd
Where
d = Diameter of the bar.

23. 23 | P a g e
SAQIB IMRAN 0341-7549889 23
σs = Stress in the bar at the section considered as design load.
τbd = Design bond stress.
LAP LENGTH:
Lap length is the overlapping length of two bars side by side which gives required
design length. In RCC structure if the length of a bar is not sufficiently available to make
design length, lapping is done.
Suppose we need to construct a building of 20 m height. But there is no 20 m single
bar available in the market. The maximum length of rebar available in the market is
usually 12 m, so we need to join two bars of 12 m to get 20 m bar.
The lap length varies from member to member.
Lap length for tension members = 40d
Lap length for compression members = 50d.
Where, d = Diameter of bars.

24. 24 | P a g e
SAQIB IMRAN 0341-7549889 24
In the below image you can see some amount of rebar is left for future construction.
This extra rebar will be needed for tying bars of column. This extra length of rebar is
called lap length.
TYPES OF BRIDGES
TYPES OF BRIDGES:
The most common types of bridges are described below:
1. BEAM BRIDGE:
Beam bridges are the simplest bridge type normally consists of one or more spans,
supported by abutment or pier at each end. Beam bridges are usually constructed of
RCC or steel or a combination of both RCC and Steel. The concrete elements used in
beam bridges may be reinforced, prestressed or post-tensioned.

25. 25 | P a g e
SAQIB IMRAN 0341-7549889 25
Types of beam bridges are girder bridge, box girder bridge, plate girder bridge etc.
2. ARCH BRIDGE:
As the name suggests, arch bridge consists of curve-shaped abutment at each end.
Generally, the roadway of bridge lies on the arch structure. The arch squeezes together
and this squeezing force is carried along the curve to support at each end. The
abutments then push back on the arch and prevent the arch ends from spreading apart.
The span of arch bridges is normally up to 800 feet and made of stone, steel, or
concrete.

26. 26 | P a g e
SAQIB IMRAN 0341-7549889 26
Types of arch bridge:
1. Hinge-less arch bridge
2. Two hinged arch bridge.
3. Three hinged arch bridge
4. Tied arch bridge.
3. CANTILEVER BRIDGE:
Cantilever bridge is constructed using cantilever span, i.e the span is supported at one
end and the other end is opened. Usually, two cantilever parts are joined to make the
roadway.
4. SUSPENSION BRIDGE:
In suspension bridge, the deck slab is suspended using ropes, chains or high tensile
strength steel cables. The roadway hangs from massive steel cables, which are draped
over two towers and secured by anchors on both ends of the bridge. The anchors are
made from solid concrete blocks. The cables transfer the loads into compression in the
two towers. usually, this type of bridge can span 2000 – 7000 feet.

27. 27 | P a g e
SAQIB IMRAN 0341-7549889 27
5. CABLE-STAYED BRIDGE:
Cable-stayed bridges are similar to suspension bridges as they also use cables but in
different form. They consist of fewer cables and the height of the towers is much
greater than suspension bridge.
6. TRUSS BRIDGE:
The superstructure of truss bridge is constructed by using trusses which are comprised
of many small elements forming triangular trusses. Truss is used because it is very rigid
structure and it can transfer the load from a single point to much wider area.

28. 28 | P a g e
SAQIB IMRAN 0341-7549889 28
PILE CAP DESIGN GUIDE
PILE CAP DESIGN GUIDE:
A pile cap is a thick concrete mat that rests on concrete or timber piles that have been
driven into the soft or unstable soil to provide a suitable and stable foundation.

29. 29 | P a g e
SAQIB IMRAN 0341-7549889 29
DESIGN GUIDE:
The pile cap should be primarily designed considering the punching shear, for the
punching shear around the heads of the piles and around the column base.
Pile cap should also be designed for bending moment due to the transmission of loads
from columns to the individual piles.
SHAPE OF PILE CAP:
The shape and plan dimensions of the pile cap depend on two factors.
1. Number of piles in the group and
2. The spacing between each pile.
The most common shapes of pile caps are given below:
Triangular pile cap for 3 piles

30. 30 | P a g e
SAQIB IMRAN 0341-7549889 30
Hexagonal pile cap for 6 to 7 piles
Rectangular pile cap for all other no. of piles.
The shapes of the pile caps minimize the plan area for symmetrical pile arrangement
about the load.
The pile cap should overhand the outer piles by at least 150mm but should not be
excessive, generally not more than the diameter of the pile diameter.
DEPTH OF PILE CAP:
The overall depth of the pile cap shall be such that it provides sufficient bond length for
the pile reinforcement and the column reinforcement.
The depth of the pile cap is decided by the following criteria.

31. 31 | P a g e
SAQIB IMRAN 0341-7549889 31
1. Punching shear.
2. Pile anchorage.
3. Shrinkage and swelling of the soil.
4. Frost attack.
5. Groundwater table etc.
But from all the above criteria, the most important criteria is shear capacity of the pile
(Beam and punching shear) which affect the selection of the pile depth.
Suitable depth of the pile cap for different diameters of pile:
Diameter of pile (in mm) Depth of pile (in mm)
300 700
350 800
400 900
450 1000
500 1100
550 1200
600 1400
750 1800
SECONDARY REINFORCEMENT:
The secondary reinforcement is provided to prevent the piles from splaying outwards
from the pile cap.
1. This reinforcement shall be provided at the bottom of the pile cap running around the
longitudinal reinforcement projecting from the piles into the pile cap.

32. 32 | P a g e
SAQIB IMRAN 0341-7549889 32
2. The direction of the secondary reinforcement should be changed at the head of each
pile.
The amount of secondary reinforcement changing its direction at the head of the each
pile shall be not less than 20% of the main tensile reinforcement and should be well
bonded.
TYPES OF COLUMN FAILURE
TYPES OF COLUMN FAILURE:
Columns are the most important parts of a structure. They transfer loads of the structure
to the surrounding soil through the foundations. So we need to build strong columns,
otherwise, failure will occur.
Columns are built with two building materials, concrete and steel. Before designing the
columns, civil engineers should calculate total stress due to live and dead load of the
building. When the applied stress exceeds the permissible stress (calculated) the
structure will fail.
In this article, different types of column failures are discussed.
1. COMPRESSION FAILURE:
When columns are axially loaded, the concrete and steel will experience some stresses.
When the loads are greater in amount compared to the cross-sectional area of the
column, the concrete and steel will reach the yield stress and failure will be starting
without any later deformation.
In this type of failure, the material fails itself, not the whole column. This type of failure
mostly occurs in shorter and wider columns. To avoid this, the column should be made
with sufficient cross-sectional area compared to the allowable stress.

33. 33 | P a g e
SAQIB IMRAN 0341-7549889 33
2. BUCKLING FAILURE:
Buckling failure generally occurs in long columns. Because they are very slender and
their least lateral dimension is greater than 12. In such condition, the load carrying
capacity of the column decreases very much.
The columns tend to become unstable and start buckling to sideward even under small
loads.That means the concrete and steel reached their yield stress for even small loads
and start failing due to lateral buckling.
This type of failures can be avoided by not constructing long columns of slenderness
ratio greater than 30.

34. 34 | P a g e
SAQIB IMRAN 0341-7549889 34
DIFFERENCE BETWEEN MAIN BARS AND DISTRIBUTION BARS
DIFFERENCE BETWEEN MAIN BARS AND DISTRIBUTION
BARS:
In any reinforcement detailing there are two sizes of bars used in the slab. That is main
reinforcement bars and distribution bars. In this article, we will discuss the difference
between main bars and distribution bars.
To understand properly we need to know the bending moment on slab.
Let’s take an example.

35. 35 | P a g e
SAQIB IMRAN 0341-7549889 35
When load is applied to a slab the bottom of the slab will experience positive moment
(Sagging) and the supports will experience negative moments (Hogging). The bottom
part, as well as the top part of the slab, will experience high tension at the same time.
The deflection will be very high in shorter span and low in longer span. High amount of
tension will be acting in the support which is near than the other one.
FUNCTION OF MAIN REINFORCEMENT BARS:
Main reinforcement bar is provided at the shorter span direction in order to transfer the
bending moment developed at the bottom of the slab. The purpose of providing main
bar is to transfer the bending load developed at the bottom of the slab to the beams.

36. 36 | P a g e
SAQIB IMRAN 0341-7549889 36
1. Main reinforcement bar is provided at the bottom of the slab at the shorter direction.
2. Stronger dimension bar is used as main bar.
In one way slab, the slab is supported by beams on the two opposite sides where main
reinforcement bar is provided.
In two way slab, the slab is supported by beams on all four sides. So there will be no
difference in bar size because each side will have to transfer equal amount of stress
evenly.
FUNCTION OF DISTRIBUTION BARS:
1. Distribution bars are provided to resist the shear stress, cracks developed in the
longer span.
2. Distribution bars are provided perpendicularly with the top of the main bar.
3. Lesser dimension bars are used.
4. Distribution bars are provided in the longer span direction.

37. 37 | P a g e
SAQIB IMRAN 0341-7549889 37
DIFFERENCE BETWEEN MAIN BARS AND
DISTRIBUTION BARS:
1. Main reinforcement bar is normally used at the bottom of the slab.
Distribution bars are placed on the top of the main bar.
2. Main bar is used in shorter direction but distribution bar is used in longer span.
3. Higher dimension bar is used as main reinforcement bar.
Lower dimension bar is used as distribution bars.
4. Main reinforcement bar is used to transfer the bending moment to beams.
Distribution bars are used to resist the shear stress, and cracks developed at the top of
the slab.
HOW TO CALCULATE CUTTING LENGTH OF BENT UP BARS IN SLAB
CUTTING LENGTH OF BENT UP BARS IN SLAB:
As a site engineer, you need to calculate the cutting length of bars according to the slab
dimensions and give instructions to the bar benders.
For small area of construction, you can hand over the reinforcement detailing to the bar
benders. They will take care of cutting length. But beware, that must not be accurate.
Because they do not give importance to the bends and cranks. They may give some
extra inches to the bars for the bends which are totally wrong. So it is always
recommended that as a site engineer calculate the cutting length yourself. In this article,
we will discuss how to the calculate length for reinforcement bars of slab. Let’s start with
an example.
EXAMPLE:
Where,
Diameter of the bar = 12 mm

38. 38 | P a g e
SAQIB IMRAN 0341-7549889 38
Clear Cover = 25 mm
Clear Span (L) = 8000
Slab Thickness = 200 mm
Development Length(Ld) = 40d
CALCULATION:
Cutting Length = Clear Span of Slab + (2 x Development Length) + (2 x inclined length)
– (45° bend x 4) – (90° bend x 2)
Inclined length = D/(sin 45°) – dD/ (tan 45°) = (D/0.7071) – (D/1)= (1D –
0.7071D)/0.7071= 0.42 D
As you can see there are four 45°bends at the inner side (1,2,3 & 4) and two 90° bends
( a,b ).
45° = 1d ; 90° = 2d
Cutting Length = Clear Span of Slab + (2 X Ld) +(2 x 0.42D) – (1d x 4) – (2d x 2) [BBS
Shape Codes]
Where,
d = Diameter of the bar.
Ld = Development length of bar.
D = Height of the bend bar.
In the above formula, all values are known except ‘D’.
So we need to find out the value of “D”.
D = Slab Thickness – (2 x clear cover) – (diameter of bar)
= 200 – (2 × 25) – 12
= 138 mm

39. 39 | P a g e
SAQIB IMRAN 0341-7549889 39
Now, putting all values in the formula
Cutting Length = Clear Span of Slab + (2 x Ld) +(2 x 0.42D) – (1d x 4) – (2d x 2)
= 8000 + (2 x 40 x 12) +(2 x 0.42 x 138) – (1 x 12 x 4) – (2 x 12 x 2)
∴ Cutting Length = 8980 mm or 8.98 m.
So for the above dimension, you need to cut the main bars 8.98 m in length.
WHY CRANK BARS ARE PROVIDED IN SLAB
WHY CRANK BARS ARE PROVIDED IN SLAB:
Different shape of bent up bars and cranks are provided in the slab and other structural
members. Bars are bent near the supports normally at an angle of 45°. The angle bent
may also be 30° in shallow beams where the (effective depth < 1.5 breadth).
In the above image, you can see how the bent up bars are provided in the slab.
The slab is supported at two ends. The maximum tensile stress that is positive moments
(sagging) acting in the middle of the slab and the maximum compressive stress that is
negative moments (hogging) acting at both ends of support. So bottom steel is required

40. 40 | P a g e
SAQIB IMRAN 0341-7549889 40
at the mid span and top steel resists negative moments at the supports. A bent-up bar
called as crank bar is provided to make RCC slab safe from compressive stresses.
When bent up bars are provided, the strength and deformation capacity of slabs with
bent up bars compared to slabs without bent up bars is sufficiently increased.
So crank bars are generally provided
1. To resist negative bending moment (hogging).
2. To resist shear force which is greater at supports.
3. To reduce the risk of a brittle failure of slab-column connection.
4. To reduce the amount of steel used.
5. For the economization of materials.
DIFFERENCE BETWEEN PRE-TENSIONING AND POST-TENSIONING
DIFFERENCE BETWEEN PRE-TENSIONING AND POST-
TENSIONING:
Pre-tensioning and Post-tensioning both methods are used under pre-stressing
process which has few edges over the orthodox non-stressed structures like greater
span to depth ratio, higher moment and shear capacity. These methods are generally
adopted in the making of PSC girders, sleepers etc.

41. 41 | P a g e
SAQIB IMRAN 0341-7549889 41
Difference between pre tensioning and post tensioning are as following:
PRE-TENSIONING :
1. In this method, the concrete is prestressed with tendons before it is placing in
position.
2. This method is developed due to bonding between the concrete and steel tendons.
3. Pre tensioning is preferred when the structural element is small and easy to transport.
4. In this method, similar prestressed members are prepared.
5. Pre-tensioning members are produced in mould.
POST-TENSIONING:
1. In this method prestressing is done after the concrete attains sufficient strength.
2. This method is developed due to bearing.
3. Post tensioning is preferred when the structural element is heavy.
4. In this method, products are changed according to structure.
5. Cables are used in place of wires and jacks are used for stretching.

42. 42 | P a g e
SAQIB IMRAN 0341-7549889 42
STRUCTURAL ELEMENTS OF BRIDGE
STRUCTURAL ELEMENTS OF BRIDGE:
1. DECK:
Deck is the portion which carries all the traffic.

43. 43 | P a g e
SAQIB IMRAN 0341-7549889 43
2. SUPERSTRUCTURE:
The portion which supports the deck slab and girder and connects one sub structure to
the other. That means all the elements of the bridge attached to a supporting system
can be categorized as superstructure.
3. SUB STRUCTURE:
The parts of the bridge which support the superstructure and transmits all the structural
loads of the bridge to the foundations. For example piers, abutments etc.
4. FOUNDATION:
Foundation is the portion which transmits loads to the bearing strata. Foundation is
required to support the piers, bridge towers, portal frames. Generally, piles and well
foundations such as H-pile, bore pile, pipe pile or precast concrete piles are adopted.
6. GIRDER OR BEAM:
Beam or girder is the part of superstructure which bends along the span. The deck is
supported by beams.

44. 44 | P a g e
SAQIB IMRAN 0341-7549889 44
7. BRIDGE TOWER:
It is the vertical supporting part used for cable stayed or suspension bridge. High
strength concrete and Insitu method are adopted to construct the bridge tower.
Cable stayed bridge
8. PIER CAP:
Pier cap is the topmost part of a pier which transfers loads from superstructure to the
pier. It is also known as headstock. It provides sufficient seating for the girders and
distributes the loads from the bearings to the piers.

45. 45 | P a g e
SAQIB IMRAN 0341-7549889 45
9. PIER:
Pier is the part of the substructure that supports the superstructure and transfers loads
of super structure to the foundations. Pier is suitable for spanned bridges with maximum
width of deck up to 8 m (2 traffic lanes). The shape and size of pier mainly depend on
aesthetics, site, space and economic constraints of the construction. Usually, bridge
pier is constructed by in situ method with large panel formwork.

46. 46 | P a g e
SAQIB IMRAN 0341-7549889 46
10. BEARINGS:
Bearing is a device which supports the parts of superstructure and transfers loads and
movements from the deck to the substructure and foundation. The main purpose of
providing a bearing is to permit controlled movement and decrease the stress involved.
11. PILE CAP AND PILES:
Pile is a slender member driven into the surrounding soil to resist the loads. Pile cap is a
thick reinforced concrete slab cast on top of the group piles to distribute loads.

47. 47 | P a g e
SAQIB IMRAN 0341-7549889 47
Bridge Foundation Pile Cap Process
12. BRIDGE ANCHOR:
Bridge anchor is only used in suspension and cable-stayed bridges to resist the pull
from suspension cable or counter span of the bridge.

48. 48 | P a g e
SAQIB IMRAN 0341-7549889 48
13. SUSPENSION CABLE:
It is used in suspension and cable-stayed bridges for the hanging, supporting and
counter balancing of the bridge deck.
DIFFERENCE BETWEEN WORKING STRESS METHOD AND LIMIT STATE
METHOD IN RCC DESIGN
DIFFERENCE BETWEEN WORKING STRESS
METHOD AND LIMIT STATE METHOD:
The cardinal difference between Working state method (WSM) and Limit State method
(LSM) is: WSM is an elastic design method whereas LSM is a plastic design method.
In elastic design, i.e. WSM, the design strength is calculated such that the stress in
material is restrained to its yield limit, under which the material follows Hooke’s law, and
hence the term “elastic” is used. This method yields to uneconomical design of simple
beam, or other structural elements where the design governing criteria is stress (static).
However, in case of shift of governing criteria to other factors such as fatigue stress,
both the methods will give similar design. Also, WSM substantially reduces the
calculation efforts.
Now coming to plastic design, i.e. LSM, as the name suggests, the stress in material
is allowed to go beyond the yield limit and enter into the plastic zone to reach ultimate
strength. Hence the “moment-rotation” capacity of beam, for example, is utilized making
the design more economical. However, due to the utilization of the non-linear zone, this
method involves arduous calculation.
All other differences are mostly derived from the above stated fundamental difference
along with few general differences. Some of these differences are stated below:
1) Serviceability check in case of LSM is required because after the elastic region strain
is higher, which results in more deformation, hence a check is necessary.
2) LSM is strain based method whereas WSM is stress based method.
3) LSM is non-deterministic method whereas WSM is deterministic approach.
4) The partial safety factor is used in LSM whereas Safety factor is used in WSM.
5) Characteristic values (derived from probabilistic approach) are used in case of LSM
whereas Average or statistic values are used in WSM.
TYPES OF LOADS ON STRUCTURE

49. 49 | P a g e
SAQIB IMRAN 0341-7549889 49
TYPES OF LOADS ON STRUCTURE:
The different types of loads coming on the foundation of a structure are described
below.
1. Dead Loads:
Dead loads consist of self-weight of the structure (weight of walls, floors, roofs etc). The
weight of the foundation and footings and all other permanent loads acting on the
structure. These can be computed by finding the weights of cubical contents of the
different materials used for constructing the structure.
2. Live Loads:
Live loads consist of moving or variable loads like people, furniture, temporary stores
etc. It is also called super-imposed load.

50. 50 | P a g e
SAQIB IMRAN 0341-7549889 50
3. Wind Loads:
The Wind acts horizontally on the surfaces of the walls, roofs and inclined roof of the
structure. That means it exerts uniform pressure on the structural components on which
it acts and tends to disturb the stability of the structure.
The value of wind loads varies depending on several factors such as geographical
location of the structure, height of the structure, duration of wind flow etc.
4. Snow Loads:
The amount of snow load depends on various factors such as shape and size of roof
structure, roofing materials, location of the structure, insulation of the structure, duration,
and frequency of snow.

51. 51 | P a g e
SAQIB IMRAN 0341-7549889 51
5. Seismic Load:
These loads are internal forces which act on the structure due to earthquake developed
ground movements.
TYPES OF RCC BEAM
RCC BEAM:
Beam can be defined as a structural member which carries all vertical loads and resists
it from bending. There are various types of materials used for beam such as steel,
wood, aluminum etc. But the most common material is reinforced cement concrete
(RCC).
Depending upon different criteria RCC beam can be of different types such as –
Depending upon shape beams can be T-beam, rectangular beam, etc.
Depending upon placement of reinforcement – singly reinforced beam, doubly
reinforced beam etc.
In this article, we will discuss different types of RCC beam depending upon their
supporting systems.
TYPES OF RCC BEAM:
Depending upon their supporting system RCC beam can be classified into four
categories as follows

52. 52 | P a g e
SAQIB IMRAN 0341-7549889 52
1. SIMPLY SUPPORTED BEAM:
This beam contains only a single span which is supported by two supports at both of the
ends.
2. CONTINUOUS BEAM:
The beam which is supported by more than two supports and continues as straight line
along its length is known as continuous beam.
3. SEMI-CONTINUOUS BEAM:
This type of beam contains two spans with or without restraint at both ends.
4. CANTILEVER BEAM:
This beam is supported by only one end and the other end is exposed beyond the
wall/support. That means one end is fixed and the other end is opened.
HOW TO CALCULATE UNIT WEIGHT OF STEEL BARS

53. 53 | P a g e
SAQIB IMRAN 0341-7549889 53
CALCULATION OF UNIT WEIGHT OF STEEL BARS:
After estimating it is very important to know the unit weight of steel bars because, we
estimate as 100 meter 20mm ø bar or 100 feet 16mm ø bar, etc (ø is the symbol of
diameter).
But steel bar suppliers will not understand this notation, they measure the steel bars in
weight. So we have to order them in kg or quintal or ton. In this article, we will discuss
how to calculate unit weight of steel bars of different diameter.
The formula is W = D²L/162
Where
W = Weight of steel bars.
D = Diameter of steel bars in mm.
L = Length of bars in meter.
Example 1: Calculate the weight of 60 meters long 12 mm ø bar.
Here, D = 12 mm.
L= 60 m.
We know that, W = D²L/162
W = 12² x 60/162 = 53 kg
Weight of 60 m 12mm ø bar is 53 kg.
Let’s look for another example.
Example 2: Calculate the weight of 100 m 16 mm ø bar.
Here, D = 16 mm.

54. 54 | P a g e
SAQIB IMRAN 0341-7549889 54
L = 100 m.
W = 16² x 100/162 = 158 kg.
If we put 1 meter length for each diameter of steel bar in the formula then we will get the
unit weight.
 10mm ø bar = 10² x 1/162 = 0.617 kg/m
 12mm ø bar = 12² x 1/162 = 0.888 kg/m
 16mm ø bar = 16² x 1/162 = 1.580 kg/m
 20mm ø bar = 20² x 1/162 = 2.469 kg/m
If we multiply the length of bars with this unit weight we will get the total weight of steel
bars.
For example, total weight of 1000 meter long 20mm ø steel bar is,
1000 x 2.469 = 2469 kg.
Using the same method we can calculate the unit weight of different steel bars.
Here I have calculated in meter but we can also calculate in foot. To calculate in foot we
have to use the following formula:
W= D²L/533
Where D = Diameter of bars in mm.
L = Length of bars in foot.
PREPARATION OF BAR BENDING SCHEDULE
BAR BENDING SCHEDULE:
Bar bending schedule or BBS is a list of reinforcement bars in tabular form which
provides the following important details:
1. Bar mark, which indicates the right position of the bar in a structure.
2. The diameter of the bar.
3. The shape of the bar.
4. The dimension of bending of the bar.
5. The number of same bar types.
6. The length of all bars.
7. Total length.

55. 55 | P a g e
SAQIB IMRAN 0341-7549889 55
8. Weight .
9. Total weight.
From BBS we can know the reinforcement of different bar sizes and bars are cut and
bent appropriately at the job site. It also ensures proper checking and completion of
estimates in a short time. The dimension of bends should be so given in the BBS that
minimum calculation is required for the making of bars and furtherly setting the machine
and stops.
PREPARATION OF BAR BENDING SCHEDULE:
The shapes and proportions of hooks and bends in the reinforcement bars are shown in
Fig. 1– these are standard proportions that are conformed to:
(a) Length of one hook = (4d ) + [(4d+ d )] – where, (4d+ d ) = 9d. (Curved portion)
(b) The additional length (la) that is introduced in the simple, straight end-to-end length
of a reinforcement bar due to bending at θ° say 30o to 60o, generally, 45o is considered)
∴ la= l1 – l2
Fig 1: Hooks and bends in Reinforcement
Let θ = 30°, 45°, 60° respectively

56. 56 | P a g e
SAQIB IMRAN 0341-7549889 56
The length of hooks and the total length of a given steel reinforcement is achieved by
the following method.
Fig 2: Typical Bar Bending Schedule
DESIGN OF RCC COLUMNS
DESIGN OF COLUMNS:

57. 57 | P a g e
SAQIB IMRAN 0341-7549889 57
The safe axial load carrying capacity of different types of columns can be determined as
follows:
1. SHORT COLUMN HAVING LATERAL TIES OR
BINDERS:
Where σcc = Permissible stress in concrete in direct compression.
Ac = (A-Asc) Net cross-sectional area of concrete excluding any finishing material and
reinforcing steel.
σsc = Permissible compressive stress for column bars.
Asc = Cross-sectional area of longitudinal steel.
P = Safe load carrying capacity of the column.
2. SHORT COLUMN WITH HELICAL
REINFORCEMENT:
These columns are reinforced with closely and uniformly spaced spiral reinforcement in
addition to longitudinal steel. These columns are also known as circular columns and
are generally spirally reinforced. Sometimes, individual loops may be used instead of
spirals. Columns having helical reinforcement shall have minimum 6 longitudinal bars.
For columns with helical reinforcement, the permissible load satisfying the requirements
shall be adopted as 1.05 times the permissible load of a similar member of lateral ties.
Note: the ratio of the volume of helical reinforcement to the volume of the core shall not
be less than
Where Ag = Gross area of the section.

58. 58 | P a g e
SAQIB IMRAN 0341-7549889 58
Ac = Area of the core of the helically reinforced column which is measured to the
outside diameter of the helix.
fck = Characteristic compressive strength of concrete.
fy = Characteristic strength of the helical reinforcement but not more than 415 N/mm2
PITCH OF HELICAL REINFORCEMENT:
Helical reinforcement should be in the regular form having the turns of the helix evenly
spaced and the ends should be anchored accurately by giving one and half extra turns
of the spiral bar.
The pitch of the helical turns shall not be greater than 75 mm, nor more than 1/6th of the
core diameter of the core diameter of the column. nor less than 25 mm, nor less than
three times the diameter of the steel bar forming the helix.
DIAMETER OF THE HELICAL REINFORCEMENT:
The diameter of the helical reinforcement shall be not less than 1/4th the diameter of the
largest longitudinal bars and in no case less than 5 mm.
3. LONG COLUMNS:
When the ratio of the effective length and the least lateral dimension of a column
exceeds 12, the column will be considered as long column. In the design of such
columns considering the factor of buckling, lower value of working stresses in steel and
concrete is adopted, by multiplying the general working stresses by the reduction
coefficient Cr.
So for long column,
Safe stress in concrete = Cr × Corresponding safe stress for short column and
Safe stress in steel = Cr × Corresponding safe stress for short column.
The reduction coefficient can be obtained by the following formula
For more exact calculation

59. 59 | P a g e
SAQIB IMRAN 0341-7549889 59
Where Cr = Reduction coefficient.
lef = Effective length of the column.
b Least lateral dimension.
rmin = Least radius of gyration.
PERMISSIBLE STRESSES IN RCC COLUMNS:
1. Permissible stresses in concrete (IS: 456-1978) :
M15 – 4 N/mm2
M20 – 5 N/mm2
M25 – 6 N/mm2
2. Permissible Stresses In Steel:
For column bars compression
σsc = 130 N/mm2
For helical reinforcement
σsh = 100 N/mm2.
DESIGN STEPS FOR RIVETED JOINT
DESIGN STEPS FOR RIVETED JOINT:

60. 60 | P a g e
SAQIB IMRAN 0341-7549889 60
For the structural steel work design transferred force by the joint is known and riveted
joint is designed for this force.
1. Adopt acceptable size of the rivet by Unwin’s formula as given below
d = 1.91√t
Where
d = Nominal Dia. of the rivet expressed in cm.
t = Plate thickness in cm.
By Unwin’s formula, the diameter of the rivet is determined and rounded to the nearest
size of the rivet.
2. In order to find out the rivet value (R) the adopted rivet, allowable bearing stress and
shearing stress should be considered.
3. Calculate the required number of rivets to oppose the force of the member by dividing
the total force to be opposed by the rivet value.
4. The rivets are commonly arranged in the diamond pattern and the width of the
member is calculated by considering tearing failure of the plate weakened by only one
rivet hole.
LAP LENGTH OF BARS
LAP LENGTH:
Development length and lap length are two important terms in reinforcement. But many
of us get confused with the difference between development length and lap length. In

61. 61 | P a g e
SAQIB IMRAN 0341-7549889 61
our previous article we have already discussed what is development length of bars,
today we will discuss what is lap length of bars.
During placing the steel in RC structure if the required length of a bar is not sufficiently
available to make a design length then lapping is done. Lapping means overlapping of
two bars side by side to achieve required design length.
Suppose, we need to build a 100 feet tall column. But practically 100 ft long bar is not
available and it is also not possible to cage. Therefore we need to cut the bars in every
second story. Now, we need to transfer the tension forces from one bar to the other at
the location of discontinuity of bar. So we have to provide the second bar closed to the
first bar that is discontinued and overlapping is to be done. The amount of overlapping
between two bars is known as lap length.
In case of RCC structure, if the length of reinforcement bars need to be extended,
splicing is used to join two reinforcement bars for transferring the forces to the joined
bar.
LAP LENGTH FORMULA:
LAP LENGTH IN TENSION:
The lap length including anchorage value of hooks shall be
1. For flexural tension – Ld or 30d whichever is greater.
2. For direct tension – 2Ld or 30d whichever is greater.
The straight length of lapping shall not be less than 15d or 20 cm.
LAP LENGTH IN COMPRESSION:
The lap length in compression shall be equivalent to the development length in
compression computed but not less than 24d.

62. 62 | P a g e
SAQIB IMRAN 0341-7549889 62
FOR DIFFERENT DIAMETER BARS:
In case of bars having different diameter are to be spliced, the lap length is calculated
on the basis of smaller diameter bar.
LAP SPLICES:
Lap splices should not be used for the bars having larger dia than 36 mm. In that case,
welding should be done. But if welding is not practicable then lapping may be permitted
for the bars larger than 36 mm dia. Additional spirals should be provided around the
lapped bars.
LAP LENGTH FOR CONCRETE OF 1:2:4
NOMINAL MIX:
Lap length in tension (for plain Grade-1 MS bar) including anchorage value is 58d. So
eliminating the anchorage value the lap length = 58 – 2*9d = 40d
where 9d = hook allowance of bars up to 25 mm and k=2
Lap length for compression bar is equal to the value of development length calculated
i.e 43.5d.
LAP LENGTH FOR M20 CONCRETE:
Columns – 45d
Beams – 60d
Slabs -60d.
So if we need to lap 20 mm dia column bars, we have to provide a minimum lap of 45 *
20 = 900 mm.
DEVELOPMENT LENGTH OF BARS
DEVELOPMENT LENGTH OF BARS:
The development length can be characterized as the length of the bar required for
transferring the stress into the concrete.
A development length is the quantity of the rebar length that is actually required to be
enclosed into the concrete to make the desired bond strength between two materials
and furthermore to produce required stress in the steel at that area.
The development length Ld of a bar is calculated as following

63. 63 | P a g e
SAQIB IMRAN 0341-7549889 63
Where d = diameter of the bar.
σs = stress in the bar at the section considered as design load.
τbd = Design bond stress.
In the below example, we need 10 db development length at the end section so that the
concrete-steel bond stays continuous. The bar is bent because there is no space
available at the end section. You can see that only 90-degree configuration is used but
here we can use more configuration like that.
The ascertained compression or tension reinforcement at every section of an RC
member is produced on both sides of that section by hooks embedded length or
mechanical gadgets.
If the restraining section of concrete is relatively thin and unable to withheld the position
of highly stressed bars the development length is given. In this way, the splitting of bars
from concrete is avoided.
The additional embedded length is known as development length. The main aim is to
give proper and settled support to the bars.
In compression reinforcement, hooks are not provided but where no or little space is
available for extra length, hooks can be used for restraints.
SINGLY REINFORCED BEAM DESIGN PROCEDURE

64. 64 | P a g e
SAQIB IMRAN 0341-7549889 64
SINGLY REINFORCED BEAM:
Singly Reinforced Beam Design
When the area of steel is provided in tension zone only i.e the reinforcement is given
only in tension zone, it will be known as singly reinforced beam.
In singly reinforced beam, the reinforcement carries the ultimate bending moment and
tension due to bending of the beam. On the other hand, the concrete carries the
compression of that beam.
The actual NA of singly reinforced beam is calculated by the below given formula.
Generally, these types of beams are balanced, under reinforced or over reinforced type.
In practical work, there is no such way to use reinforcement only in tension area,
because we have to bind the stirrups. So, in the compression zone, always two rebars
are used to bind the stirrups where, the rebars just withstand those stirrups.
SINGLY REINFORCED BEAM DESIGN PROCEDURE:
1. Determine the value of N by the following formula:
[Where N = Critical N.A Constant.]
2. Find the value of J.

65. 65 | P a g e
SAQIB IMRAN 0341-7549889 65
Where J = Lever arm constant
3. Determine the moment of resistance coefficient
4. Select appropriate breadth (b) and equate the bending moment and moment of
resistance with the effective depth of the section.
5. Calculate the value of At
Where At = Area of tensile steel.
t = Allowable tensile stress in steel.
GIRDER DESIGN PROCEDURE

66. 66 | P a g e
SAQIB IMRAN 0341-7549889 66
GIRDER DESIGN PROCEDURE:
Girder Design
The design of girder or built up beam is done by trial and error method. The section of
the girder is chosen and checked for the stresses. The general steps of girder design
are as following.
1. Calculate the bending moment to be opposed by the beam with respect to loads and
span of the beam.
Let the maximum bending moment to be opposed is M, and maximum shear force is F.
2. Calculate the suitable measure of modulus of section by the below given formula.
Z = M/P
where P = Permeable bending stress.
3. Select a rolled steel section.
If the modulus of section is small than the required amount of Z, extra cover plates
might be included on the both flanges to get required value of Z.The girder sections now
checked against bending stresses in extreme fibers.
5. The section of the girder should also be checked for shear force and deflection/
Shear stress of the section is calculated by the below formula
q = F/tw* h

67. 67 | P a g e
SAQIB IMRAN 0341-7549889 67
where q = Shear stress
tw =Web thickness,
h = depth of the beam.
The value of q should not cross 94.5 N/mm2. Permeable deflection should not cross
L/325 limit.
Where L = Effective span of the beam.
R.C.C T-BEAM
RCC T-BEAM:
The beam consists of a flange and a rib in the form of a T, generally made of RC
concrete or metal is known as T-beam. The top part of the Slab which acts along the
beam to resist the compressive stress is called flange. The part which lies below the
slab and resists the shear stress is called rib.

68. 68 | P a g e
SAQIB IMRAN 0341-7549889 68
DIMENSION OF T-BEAM:
1. The effective width of the flange is adopted as the minimum of c/c distance of the
nearby ribs or beams.
2. The overall thickness of the slab crossing over the beam is taken as flange thickness.
3. The breadth of the rib is taken on down earth ground. It should be adequate to hold
the steel zone in it, effectively. It might be taken as between 1/3 to 2/3 of the general
depth of the beam.
4. The depth of the T-beam is taken between 1/10 tp 1/20 of the span, contingent on the
loads acting on it. It can be likewise accepted from the economy point by the given
formula:
Where,
r = Proportion of the cost of steel to the cost of concrete.
br = Breadth of rib.
M = Maximum bending moment.
N.A OF T-BEAM:
The actual NA is calculated by the given formula.

69. 69 | P a g e
SAQIB IMRAN 0341-7549889 69
Formula 1 is used when the NA is resting under the bottom area of the slab, i.e NA is in
the rib and formula 2 is used when NA is resting in the flange of the slab.
As the compressive area of the rib is extremely small, it is always neglected.
MOMENT OF RESISTANCE OF T-BEAM:
Mr = Total compression * Lever arm
Where,
c = compressive stress in the concrete acting bellow the flange.
y = Distance of center of gravity of the compressive force acting under the outermost
fiber.
The critical NA is calculated by the same equation used for singly reinforced beam.
To determine NA of the T-beam, first, we need to know the area of the steel. It can be
evaluated by taking the value of j as 0.9 or on the other hand accepting the center of
gravity of the compressive force is lying at mid-depth of the flange slab.
COMBINED FOOTING

70. 70 | P a g e
SAQIB IMRAN 0341-7549889 70
COMBINED FOOTING:
Combined Footing
A footing when used for two columns or more than two columns is called combined
footing. Combined footing is mainly two types.
1. Rectangular Combined Footing.
2. Trapezoidal Combined Footing.
This type of footing is provided under following situations:
1. When the columns are located extremely close to each other and their individual
footings are overlapping.
2. In case of soil having low bearing capacity and a large area is required under the
individual footing.
3. When the column end is situated near the property line and it is not possible to
extend the footing area on the side of the property line.
The main purpose of using combined footing is to distribute uniform pressure under the
footing. To accomplish this target, the center of gravity of the footing area should be
equal to the center of gravity of the two columns.
If the outside columns close to the property line, conveys heavier load, it is necessary to
provide trapezoidal footing to maintain the center of gravity of the footing in line with the
center of gravity of the two column loads. Otherwise only a rectangular footing may be
provided. Following extra points should be kept in view to provide combined footings.
1. This type of footing is considered as an inverted floor, where footing load is carried by
the columns and loaded from underneath by uniform earth reaction.
2. The area enclosed by combine footing should be equivalent to or more than that
acquired by dividing the total combined load into the columns by safe bearing capacity
of the soil.
3. The shape of the combined footings should be selected in such a manner that it
concurs the center of gravity with the center of gravity of soil reaction.

71. 71 | P a g e
SAQIB IMRAN 0341-7549889 71
ISOLATED COLUMN FOOTING DESIGN
ISOLATED COLUMN FOOTING DESIGN:
Generally, isolated column footing is square, rectangular or circular in shape. The upper
surface of this footing may be flat i.e horizontal, stepped or sloped. The footing is
provided with slope or steps to protect the concrete and impact economy.
DEPTH OF THE FOOTING:
The following two points should be considered for the design of footing depth.
1. Maximum bending moment about the column face.
2. Punching shear about the column perimeter.
1. DEPTH OF THE FOOTING FROM BM CONSIDERATION:
Let, B = Length of the sides of square footing.
b = Length of the sides of the square column.
p = Upward soil pressure.
In the footing slab, the critical section for BM is at the column face. It acts as a
cantilever loaded slab with the total upward soil pressure p. Consider the rectangular
area of the footing to calculate the column face. (As shown in the Figure)
BM calculation about the face of the rectangle:

72. 72 | P a g e
SAQIB IMRAN 0341-7549889 72
Effective depth of the footing = √BM/Rb
2. DEPTH OF THE FOOTING ON PUNCHING SHEAR:
The slab thickness of the footing should be adequate to oppose the inclination of the
column for punching shear through the slab.
The critical section for punching shear is considered at d/2 from the face of the column.
(As per IS 456-1978)
Depth based on this consideration:
Where Sp = Allowable shear stress.
The footing depth is assumed greater than the two values.
The slab of the foundation must be checked for shear and bond.
MINIMUM THICKNESS OF THE FOOTING SLAB AT FREE
EDGE:
When the footing slab is laying on the soil minimum thickness of 15 cm at the edges
should be used. When the footing slab is laying on piles, the minimum thickness at the
edges is considered as 30 cm.
CAUSES OF FAILURE OF PILES
CAUSES OF PILE FAILURE:
The various causes of pile failure are as following

73. 73 | P a g e
SAQIB IMRAN 0341-7549889 73
1. When pile load is greater than the design load.
2. Poor and defective workmanship while casting the pile.
3. Dislocation of reinforcement while casting.
4. Bearing pile laying on delicate strata.
5. Inappropriate characterization of soil.
6. Incorrect selection of pile types.
7. Inadequate reinforcement in the pile.
8. Corrosion of the timber pile because of assault by insects.
9. Buckling of the piles because of insufficient lateral support.
10. Defective techniques used while driving the pile.
11. Inaccurate determination of the bearing capacity of the pile.
REINFORCEMENT DETAILS IN ONE WAY SLAB
ONE WAY SLAB REINFORCEMENT:
When a slab is supported on the two different sides and the ratio of longer span to
shorter span is more than 2, it will be considered as one way slab. In one way slab, one
side is larger than the other one.
In one way slab, as one side is greater than the rest one, the maximum load is
conveyed by the larger side just so giving main reinforcement comparing to that load
conveying side will be adequate.
To provide adequate support on the bigger side, main reinforcement is given
perpendicular to that side or parallel to the shorter direction. Distribution steel is
provided in the longer direction, which won’t help in conveying any load.

74. 74 | P a g e
SAQIB IMRAN 0341-7549889 74
ONE WAY SLAB REINFORCEMENT DETAILS:
For one way slab, main reinforcement is computed by a formula (In limit state design)
that is determined by comparing compressive force as well as tensile forces.
Ast = 0.5 Fck/Fu[1-√1-2.6Mu/Fck.b.d]b.d
and the distribution steel is computed as
0.15% of Ag, for mild steel.
0.12% of Ag, for tor steel.
Where Ast = Area of the steel in tension.
Fu = Ultimate strength of steel.
Mu = Ultimate moment of resistance.
b = Breadth of the slab section.
d = Depth of the slab section.
Ag = Gross area of the section.
DESIGN OF GRILLAGE FOUNDATION

75. 75 | P a g e
SAQIB IMRAN 0341-7549889 75
GRILLAGE FOUNDATION DESIGN:
Figure 1 demonstrates a simple design of a one tier grillage foundation for a steel
stanchion. The bending moment and shear force required for the grillage beam design
can easily be arrived by the following simple method.
Let, W = Load supported by one beam in N.
L = The length of the beam in m.
l = The length of the base plate in m.
Figure 1 also shows the load distribution. It is apparent the highest bending moment in
the beam
= (W/2 * L/4) – (W/2 * L/4)
= W/8(L-l) in Nm
In the beam maximum shear force develops at the edge of the base plate. The upward
pressure of soil on the beam = W/L N/m
Cantilever projection of the beam beyond the edge of the base plate
= (L-l/2)
Maximum shear force in the beam = W/L (L-l/2)
BALANCED, UNDER REINFORCED AND OVER REINFORCED SECTION

76. 76 | P a g e
SAQIB IMRAN 0341-7549889 76
BALANCED SECTION:
The section in which the quantity of steel is just sufficiently provided that the concrete in
compression zone and steel in tension zone reaches to their permissible stresses
simultaneously is called balanced section.
In this section, the critical depth is equal to its actual depth. i.e n = Na = Nc
UNDER REINFORCED SECTION:
In this section, the quantity of steel is not adequate to make the extreme concrete fibers
in the compression area to get compressed to their highest permissible stress.
In this section, the quantity of steel is not adequate to make the concrete to get
compressed in compression area to their highest permissible value. That means the
steel is provided less than that a balanced section is required. In under reinforced
section, the depth of actual Na is less than the critical Na.
i.e; Na<Nc.

77. 77 | P a g e
SAQIB IMRAN 0341-7549889 77
OVER REINFORCED SECTION:
In this section, the quantity of steel in tension zone is greater than the quantity of steel
required to make compressive zone concrete to get compressed to their most extreme
admissible value. In other words, when the extreme compressive stress in concrete
achieves its allowable limit, the comparing tensile stress in steel will be not as much as
its permissible value.
So in overreinforced section, the depth of actual Na is greater than the critical Na.
i.e; Na > Nc
DOUBLY REINFORCED BEAM
DOUBLY REINFORCED BEAM:
R.C.C beam which comprises of reinforcement both in tension zone, as well as
compression zone is called doubly reinforced beam.
Doubly reinforced beam is generally adopted in following conditions:
1. When the size of the beam is confined.
2. When the section of the beam is subjected to inversion stress.
3. When the beam is nonstop more than a few backings.

78. 78 | P a g e
SAQIB IMRAN 0341-7549889 78
Critical NA of a doubly reinforced beam is calculated by this given formula:
n = mcd/t+mc
Where, n = Critical NA
m = Modular ratio.
c = Max. compressive stress in the concrete.
d = Effective depth of the beam.
t = Allowable tensile stress in steel.
Actual NA is determined by taking moments of the effective zone about the centroid of
the effective segment.
bn2/2 + (1.5m-1)Ac(n-dc) = mAt(d-n)
Where, b = Breadth of the beam.
Ac = Area of compressive steel.
dc= Centre of gravity (c.g) of compressive region of steel from external fibres.
At = Area of tensile steel.
Doubly reinforced beam is inefficient in steel, as steel is utilized as a part of
compression zone is never stressed to its full limit. Compressive stress in steel relies on
the compressive stress in concrete at that level. Stress in concrete (C1) at level of
compressive steel can be determined by using following equation.
C1 = c(n-dc)/n
Moment Of Resistance In Doubly Reinforced Beam:
The total moment of resistance is calculated by adding the moments of following two
couples.
1. Couple (M1) having tensile steel A and compressive concrete.
2. Couple (M2) having extra tensile steel At and compressive steel.
The moment of resistance M = M1 + M2 = (bnc/2)(d-n/3) + (1.5-1)AcC1(d-dc)
Where C1 = c(n-dc/n)
DESIGN PROCEDURE OF R.C.C LINTEL

79. 79 | P a g e
SAQIB IMRAN 0341-7549889 79
RCC LINTEL DESIGN:
The steps of RCC lintel design (single span or continuous with a few openings) are
same as the design of a simple beam.
1. The lintel width is equal to the wall thickness.
2. Consider a suitable depth of the lintel.
3. Choose the effective span of the lintel ( consider reasonable end bearings and
effective depth).
4. Let W be the aggregate weight of the masonry work encased in the triangle, in the
event that conditions warrant triangular load of the workmanship on the lintel.
5. Calculate the maximum bending moment (M1) at the center of the lintel ( due to the
triangular load).
M1 = Wl/6
6. Now calculate the maximum bending moment (M2) due to the self-weight (w) of the
lintel per meter length.
M2 = wl^2/8
7. Total maximum bending moment at the center of the lintel is
M = M1 + M2 = Wl/6 + wl^2/8
8. Find out the effective depth (d) of the lintel by using the given formula
d = (M/Q×b)
9. Now calculate the area of steel (As)
Ast = M/t×jd
Give this zone in a type of appropriate diameter bars. Twist around 40% – 50% steel
rods up at l/7 distance from lintel end.
10. Calculate maximum shear force = W/2 + wl/2
11. Finally, check the lintel in shear and development length.
12. Give 6 mm ϕ two-legged ostensible stirrups at most extreme c/c spacing of the lever
arm (jd).
DIFFERENCE BETWEEN PRIMARY, SECONDARY AND TIE BEAM

80. 80 | P a g e
SAQIB IMRAN 0341-7549889 80
Beam is one of the most important structural parts of a building. In our previous article,
we have already discussed different types of beams used in construction. In this article,
we will discuss the differences between primary, secondary and tie beam.
PRIMARY BEAM:
The beams that are connecting columns for transferring loads of a structure directly to
the columns are known as primary beams. Usually, primary beams are shear connected
or simply supported and they are provided in a regular building structure. The depth of
the primary beams is always greater than secondary beams. Primary beam act as a
medium between columns and secondary beams.
SECONDARY BEAM:
The beams that are connecting primary beams for transferring loads of a structure to
the primary beams are known as primary beams. These beams are provided for
supporting and reducing the deflection of beams and slabs.
TIE BEAM:
The beams that are connected by two or more rafters in the roof or roof truss for
stiffening the whole building structure, known as tie beams.

81. 81 | P a g e
SAQIB IMRAN 0341-7549889 81
These beams do not carry the vertical load of slab or walls instead carry the axial
compression. Generally, tie beams are used in roof truss or in damp proof course at the
plinth level.
REINFORCEMENT DETAILS IN BEAMS AND SLABS
BEAM REINFORCEMENT DETAILS:
Beams are essentially provided with main reinforcement on the tension side for flexure
and transverse reinforcement for shear and torsion.
TENSION REINFORCEMENT:
The minimum tension reinforcement is denoted by the given formula
As = (0.85bd/fy)
Where, As = Minimum quantity of tension reinforcement
b = breadth of the beam,
d = effective depth,
fy = strength of reinforcement in N/mm2
D = Overall depth of the member.
The minimum tension reinforcement (As) should not be less than the value of
(0.85bd/fy).
And the maximum quantity of tension reinforcement should not be greater than the
value of 0.04bd.
COMPRESSION REINFORCEMENT:
Stirrups should be provided with the compression reinforcement in beams for lateral
restraint.

82. 82 | P a g e
SAQIB IMRAN 0341-7549889 82
The maximum quantity of compression reinforcement should not cross 0.04bd.
SIDE FACE REINFORCEMENT:
At the point when the depth of web or rib in a beam crosses 750 mm, the side face
reinforcement of cross sectional area at the very least 0.01% of the web zone is to be
given and disseminated similarly on two appearances and the dividing of the bars not
cross 300 mm thickness whichever is smaller.
TRANSVERSE OR SHEAR REINFORCEMENT:
The minimum quantity of shear reinforcement is computed by the given formula
Asv ≥ (0.4bSv/0.87fy)
Where Asv = Total cross-sectional area of stirrups legs in shear.
Sv = Spacing of stirrups along the length of the member.
b = The breadth of the beam or the web in a flanged member.
fy = Characteristic strength of stirrups reinforcement, which should not cross 415
N/mm2.
For vertical stirrups, the maximum spacing of shear reinforcement should not cross
0.75d.
and for inclined stirrups d is considered as 450.
The maximum limit of spacing is 300 mm.

83. 83 | P a g e
SAQIB IMRAN 0341-7549889 83
SLAB REINFORCEMENT DETAILS:
The details of slab reinforcement are given below.
METHODS OF UNDERPINNING

84. 84 | P a g e
SAQIB IMRAN 0341-7549889 84
UNDERPINNING METHODS:
The method of providing a new foundation underneath an existing foundation without
disturbing its stability is known as underpinning. Underpinning is necessarily adopted to
replace a defective foundation or to increase the strength of an existing foundation
which enables the load conveying limits.
PURPOSE OF UNDERPINNING:
1. To replace a defective foundation into a new foundation.
2. To increase the strength of an existing foundation.
3. To increase the load carrying capacity of a structure.
METHODS OF UNDERPINNING:
1. PIT METHOD:
In this method, short length columns of 1.2 m to 1.8 m are underpinned. First, holes are
cut in the wall above the ground level at common intervals and strong needles are then

85. 85 | P a g e
SAQIB IMRAN 0341-7549889 85
inserted through the holes to carry the entire load of the structure. Generally, the
needles are made of timber beam or steel joist.
In case of RSI beams, wooden bearing plates are used between the beams and
supporting wall to minimize the masonry crushing. Jacks are provided to support the
needle beams. Jacks should be placed sufficiently away from the supporting walls to
enable the working space for trench excavation and concreting.
When a foundation is required to be replaced, the section of the wall should be cut in 90
cm – 120 cm in length for new work to be built. Again, cut the next 90 cm to 120 cm
length of the wall and rebuilt. Thus the wall foundation can be replaced.
2. PILE METHOD:
In this process, concrete piles are pushed on the both sides of the wall. The needle
beams are then used over the piles through the wall, where the needle beams act as
pile caps. It alleviates the load from the wall. This strategy is helpful for water logged
soils where walls convey heavy loads. In this situation piles and needle beams turn into
a perpetual part of the establishment and existing foundation of the walls are not
disturbed.
REINFORCEMENT DETAILS IN COLUMNS
COLUMN REINFORCEMENT DETAILS:
Generally, concrete columns consist of square, rectangular or circular cross sectional
area. Columns are essentially required with the primary longitudinal reinforcement and
lateral ties to avoid buckling of the primary bars.

86. 86 | P a g e
SAQIB IMRAN 0341-7549889 86
The details of minimum and maximum limits of reinforcements, minimum no. of bars,
the size of bars, cover requirements, diameter, and spacing are given in the above
picture.
In case of RC columns consisting helical ties, 6 basic longitudinal reinforcement must
be given to the helical support. The spacing of the longitudinal reinforcement should not
be more than 300 mm.
The maximum and minimum values of the pitch of helical reinforcement is restricted to
75 mm and 25 mm. Helically reinforced portions have considerably greater load
conveying limit than those have common lateral ties because of higher degree control of
concrete in the center.
SINGLY REINFORCED BEAM VS DOUBLY REINFORCED BEAM
SINGLY REINFORCED BEAM:
The beam that is longitudinally reinforced only in tension zone, it is known as singly
reinforced beam. In Such beams, the ultimate bending moment and the tension due to
bending are carried by the reinforcement, while the compression is carried by the
concrete.

87. 87 | P a g e
SAQIB IMRAN 0341-7549889 87
Practically, it is not possible to provide reinforcement only in the tension zone, because
we need to tie the stirrups. Therefore two rebars are utilized in the compression zone to
tie the stirrups and the rebars act as false members just for holding the stirrups.
DOUBLY REINFORCED BEAM:
The beam that is reinforced with steel both in tension and compression zone, it is known
as doubly reinforced beam. This type of beam is mainly provided when the depth of the
beam is restricted. If a beam with limited depth is reinforced on the tension side only it
might not have sufficient resistance to oppose the bending moment.
The moment of resistance can not be increased by increasing the amount of steel in
tension zone. It can be increased by making the beam over reinforced but not more
than 25% on the strained side. Thus a doubly reinforced beam is provided to increase
the moment of resistance of a beam having limited dimensions.
Besides this, doubly reinforced beams can be utilized under following conditions,
1. When the outside load is alternating, that means the load is acting on the face of
the member.
2. The load is eccentric and the eccentricity of the load is changing from one side to
another side of the axis.
3. The member is subjected to a shock or impact or accidental lateral thrust.
DESIGN STEPS OF SIMPLY SUPPORTED STEEL BEAM

88. 88 | P a g e
SAQIB IMRAN 0341-7549889 88
SIMPLY SUPPORTED BEAM DESIGN:
1. Calculate the loads to be carried by the beam.
2. Calculate the maximum bending moment (M) with regard to the nature of loading
condition and span.
3. Calculate the section modulus (Z) of the required section of the beam by the formula:
Z = M/f
where f is the safe allowable stress in steel in bending.
4. From the table “properties of beams” select a suitable section having its section
modulus slightly greater than the calculated one. In making the selection of the section,
deeper section should be preferred.
5. Calculate maximum shear force in the beam.
6. Check the section for safe shear stress by the formula:
s = (S/Ib) × Aȳ
Where
s = intensity of shear stress.
S = maximum shear force in the beam.
Aȳ = The moment of the area of the part of the section situated beyond its neutral axis.
In case of a rolled steel joists, this formula may be reduced to

89. 89 | P a g e
SAQIB IMRAN 0341-7549889 89
s = S/d×t
where d is the overall depth of the joist and t is the thickness of the web.
7. Check the selected section for its safety from consideration of allowable deflection.
ADVANTAGES OF STEEL ROOF TRUSS OVER TIMBER TRUSS
ADVANTAGES OF STEEL ROOF TRUSS OVER TIMBER
TRUSS:
A truss consists of an assembly of rigid but elastic members jointed in the form of
triangles to act as a beam. The safe working tensile stress of mild steel is about 20
times that of structural timber. Thus steel trusses work out to be economical, especially
for biggest spans. Out of the various shapes of steel sections, angles are considered
most suitable for steel roof truss. This is on account of the fact that angles can resist
both compressive and tensile stresses effectively. In additional angles can be produced
economically and can be jointed easily.
Advantages of steel roof truss over timber truss are given below:
1. Steel trusses are stronger than timber trusses.
2. Steel section forming the truss are light in weight and can be fabricated in any
desired pattern to suit the architectural requirement.
3. There is no danger of the material being eaten away by white ants or other insects.
4. Steel trusses are more fire-resisting than timber trusses.
5. They do not have span restrictions and as such steel trusses can be used for
industrial buildings and other such structures where large areas are required to be
covered without obstructions due to columns etc.
6. The sections forming a steel truss are easy in transportation.
7. The sections can be obtained in any desired form or length to suit the requirements
and there is not much wastage of the material in cutting etc.

90. 90 | P a g e
SAQIB IMRAN 0341-7549889 90
8. On account of their easy erection techniques, the progress of roofing work with steel
trusses is fast.
REASON FOR FAILURE OF CONCRETE STRUCTURES
REASON FOR FAILURE OF CONCRETE STRUCTURES:
A reinforced concrete member can fail mostly in the following cases:
1. When the member is subjected to excessive tension, so as to exceed the permissible
stress in steel.
2. When the loading is such that the compressive stress in concrete exceeds its safe
permissible value.
3. On account of the slipping of the steel bars from concrete.
4. When the concrete is subjected to excessive shear.
5. Due to the bad quality of materials used, shrinkage, creep or thermal effects.
6. When the member is subjected to extremes of temperature, aggressive liquids or
gasses.
PILE FOUNDATION – CLASSIFICATION OF PILE FOUNDATION
PILE FOUNDATION:
In pile foundation, a thin member made of steel, concrete or wood is inserted into the
poor ground (Soil having low bearing capacity) for transferring the load of a
superstructure. The load can be transmitted to a strong soil layer by friction or by
bearing.
PURPOSE OF PILE FOUNDATION:
1. The main purpose of a pile foundation is to transfer the loads into a strong stratum.
2. Generally, pile foundations are used when the bearing capacity of soil is very low and
the structural load is heavy.
3. Compressible soil and waterlogged soil is ideal for this type of foundations.
4. Piles are mostly suitable for the foundation of high-rise buildings, bridges, piers,
docks etc.
CLASSIFICATION OF PILE FOUNDATION:
Depending upon the function, material and method of installation pile foundation can be
further classified into following categories;

91. 91 | P a g e
SAQIB IMRAN 0341-7549889 91
CLASSIFICATION DEPENDING UPON THE
FUNCTION OF PILES:
1. Bearing Piles:
Bearing piles are the pile that is driven through a soft soil until it reaches to a stronger
base. These piles are used as piers to support the superstructure and to transmit the
load into a safe stratum.
2. Friction Piles:
When piles are compelled through a soft and weak soil by developing friction between
surrounding earth and outside of the pile, it is known as friction pile.
3. Sheet piles:
These piles are used on a rare occasion like retaining wall construction. It helps to
minimize the lateral subsidence of retaining soil.
4. Anchor Piles:
This pile opposes the horizontal pull by providing anchorage slip.
5. Batter Piles:
Batter piles are used to prevent horizontal and inclined forces.
6. Fender Piles:
When ships are bounded at the deck, the concrete deck being damaged. This injury of
concrete deck is protected by fender piles.
7. Compaction Piles:
Compaction piles are used to increase the bearing capacity of granular soil.
CLASSIFICATION DEPENDING UPON THE
MATERIALS OF PILES:
1. Timber piles.
2. Concrete Piles.
3. Steel Piles.
DIFFERENCE BETWEEN ONE WAY SLAB AND TWO WAY SLAB

92. 92 | P a g e
SAQIB IMRAN 0341-7549889 92
ONE WAY SLAB:
One way slab is a slab which is supported by beams on the two opposite sides to carry
the load along one direction. In one way slab, the ratio of longer span (l) to shorter span
(b) is equal or greater than 2, i.e Longer span (l)/Shorter span (b) ≥ 2
Verandah slab is a type of one way slab, where the slab is spanning in the shorter
direction with main reinforcement and the distribution of reinforcement in the transverse
direction.
TWO WAY SLAB:
When a reinforced concrete slab is supported by beams on all the four sides and the
loads are carried by the supports along both directions, it is known as two way slab. In
two way slab, the ratio of longer span (l) to shorter span (b) is less than 2.
i.e Longer span (l)/Shorter span (b) < 2
This types of slabs are mostly used in the floor of multi-storey buildings.

93. 93 | P a g e
SAQIB IMRAN 0341-7549889 93
DIFFERENCE BETWEEN ONE WAY SLABS AND TWO WAY
SLABS:
1. In one way slab, the slabs are supported by the beams on the two opposite sides.
In two way slab, the slabs are supported on all the four sides.
2. In one way slab, the loads are carried along one direction.
In two way slab, the loads are carried along both directions.
3. In one way slab, the ratio of Longer span to shorter span is equal or greater than 2.
(i.e l/b ≥ 2).
In two way slab, the ratio of l/b is less than 2 (i.e l/b < 2).