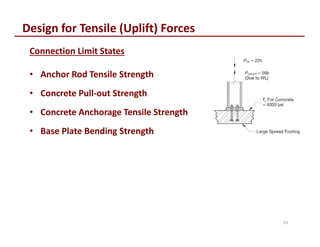
The document discusses the design and erection of column base plates. It covers types of base plates for different load cases including axial compression, tension, and combined axial and moment loads. Key topics covered include base plate and anchor rod materials, design for concrete crushing and bending, anchor rod design, and erection procedures. Diagrams illustrate critical sections and design equations for different limit states. Construction tolerances and OSHA standards for base plate design are also summarized.

1. COLUMN BASE PLATES
- DESIGN TO ERECTION –
Tom Murray
Emeritus Professor
Virginia Tech
Blacksburg, VA
1

2. Column Base Plates
2

3. Types of Column Base Plates
Compressive Axial Loads
Base Plates with Small Moments
Tensile Axial Loads
Base Plates with Large Moments
3

4. AISC Design Guide 1
4

5. AISC Specification
PERTINENT SECTIONS AND TABLES
Chapter J Design of Connections
Table J3.2 Nominal Strength of
Fasteners and Threaded Parts
J8. Column Basses and Bearing on
Concrete
Chapter M Fabrication and Erection
M2.2 Thermal Cutting
M2.8 Finish of Column Bases
M4.4 Fit of Column Compression Joints
and Base Plates
5

6. Types of Column Base Plates
TOPICS
• Base Plate and Anchor Rod Material and Details
• Base Plates for Axial Compression
• Base Plates for Tension
• Base Plates for Axial Compression and Moment
• Shear Anchorage
• Column Erection Procedures
• Result of Poor Anchor Rod Placement
6

7. Base Plate and Anchor Rod
Materials and Details
7

8. Base Plate Material, Fabrication and Finishing
Base Plate Material
• Typical A36
• 1/8” (3mm) increments to 1-1/4 in (32 mm) then ½ in. (6 mm)
• Minimum thickness ½ in. (13 mm), typical ¾ in. (20 mm)
Fabrication and Finishing
• Plate is thermally cut
• Holes drilled or thermally cut
• Specification Section M2.2 has requirements for thermal cutting
• Finishing: Specification Section M2.8
< 2 in. (50 mm) milling not generally required
2 – 4 in.(50 – 100 mm) straightened by pressing or milling
> 4 in. (100 mm) milling required
Only mill where column bears
• Bottom surface with grout need not be milled
• Top surface not milled if complete-joint-penetration (CJP) welds
8

9. Base Plate Material, Fabrication and Finishing
Base Plate Welding
• Fillet welds preferred up to ¾ in. (20 mm) then groove welds
• Avoid all around symbol
• Weld for wide-flange columns subject to axial compression
Weld on one side of column flanges
to avoid rotating the section:
• HSS subject to axial compression: Weld flats only
• Shear, Tension, Moment, and Combinations
Size weld for forces not all around
No weld at fillets of wide-flange columns
Must weld at corners of HSS if tension or moment
• Shop welded preferred
• Very heavy base plates may be field welded after grouting
9

10. Anchor Rod Materials and Details
Anchor Rod Material
• Preferred ASTM F1554 Gr 36 except when high tension and or
moment.
10

11. Anchor Rod Materials and Details
Anchor Rod Material
• Unified Course (UNC) threads
• Standard Hex Nuts permitted but Heavy Hex nuts required for
oversize holes and with high strength anchor rods.
• Hooked anchor rods have very low pull-out strength but OK for
axial compression only.
• Headed rods or rods with nuts are preferred.
Headed Rods
Rods with Nuts
11

12. Anchor Rod Materials and Details
Anchor Rod Material
• Use of plate washers at bottom of rods can cause erection
problems and should be avoided.
• Drilled-in epoxy anchor rods may be used for light loads
• Wedge-type anchors should not be used because of potential
loosing during erection.
12

13. Anchor Rod Materials and Details
Anchor Rod Holes and Washers
• Oversize holes required because of placement tolerances.
• Recommended hole and washer sizes are in Design Guide 1
(Table 2-3) and AISC 14th Ed. Manual (Table 14-2).
• Smaller holes may be used when axial compression only.
• Plate washers required when tension and/or moment.
13

14. Anchor Rods Material and Details
Anchor Rod Sizing and Layout
• Recommendations
Use ¾ in. (22 mm) minimum diameter.
Use Grade 36 rod up to about 2 in. (50 mm) diameter.
Thread at least 3 in. (75 mm) beyond what is needed.
Minimum ½ in. (12 mm) distance between edge of hole
and edge of plate.
Use symmetrical pattern whenever possible.
• Provide ample clearance for nut tightening.
• Coordinate anchor bolt placement with reinforcement location.
14

15. Occupational Safety and Health Administration (OSEA)
OSEA Safety Standards for Steel Erection (2008)
• Minimum of four anchor rods.
• Base plate to resist eccentric gravity load of 300 lb (1,300 N) 18
in. (450 mm) from extrem outer face of column in each direction.
• 300 lb (1,300) represents weight of iron worker with tools.
• Exception: Post-type columns weighing less than 300 lb.
18 in.
Note: Smallest of anchor rods on
a 4 in. by 4 in. (100 mm by 100 mm)
pattern is generally sufficient.
300 lb
15

16. Column Base Plates
DESIGN CONSIDERATIONS
• Base Plate Bending Strength
• Concrete Crushing
• Concrete Anchorage for Tension Forces
• Shear Resistance
• Anchor Rod Tension Design
• Anchor Rod Shear Design
• Anchor Rod Embedment
• Constructability
16

17. Base Plates for
Axial Compression
17

18. Design for Axial Compression
Column Base Plate Design Limit States
• Base Plate Bending
• Concrete Crushing
18

19. Design for Axial Compression
Column Base Plate Bending
fpu = Ru /(BxN) = pressure due to reaction
Let m’ = max(n and m)
Mu= fpu (1) (m’2/2 < φMp
φMp = 0.9 Fy Zx = 0.9x 1 x tp2/4) Fy
Substituting:
t p , min
=
2 f pu ( m ' 2 )
0 .9 F y
19

20. Design for Axial Compression
Column Base Plate Bending
• Lightly Loaded Base Plate
• Required concrete bearing area is less than bfdc.
d
bf
Bearing Area
20

21. Design for Axial Compression
Column Base Plate Bending
• Lightly Loaded Base Plate
Replace m′ with l = max {m, n, λn′}, where
′
′
2 X
λ =
≤ 1 .0
1+ 1-X
1
n′ =
4
db f
2f pu l 2
t p ,min =
 4db f  Pu
0.9Fy

X=
 (d + b )2  φPp
f


Reference: Thornton, W.A., Design of Base Plates for Wide Flange
Columns – A Concatenation of Methods, AISC Engineering Journal,
21
Fourth Quarter, 1990.

22. Design for Axial Compression
HSS Sections
• Bend lines.
0.95h
0.95d
0.80d
22

23. Design for Axial Compression
Concrete Crushing
Specification Section J8. Column Bases and Bearing on Concrete
φc = 0.65
(a) On the full area of a concrete support
Pp = 0.85fc′A1
(J8-1)
(b) On less than the full area of a concrete support
(J8-2)
where Pp = 0.85fc A1 A 2 / A1 ≤ 1.7fc A1
′
′
fc’ = specified compressive strength of concrete, ksi (Mpa)
A1 = area of steel bearing on concrete, in.2
A2 = area of the portion of the supporting surface that is
geometrically similar to and concentric with the
loaded area, in.2
Note: The limit < 1.7f’c is equivalent to A2/A1 < 4
23

24. Design for Axial Compression -- Example
o
24”
18”
Ex.: Determine if the base plate shown is adequate.
Column: W10x33 d = 9.73 in. bf = 7.96 in.
PL 1-½ x 18 x 1’-6” A36
Concrete Pedestal:
24 in. by 24 in. (assume square)
fc′′=3.0 ksi
Pu = 250 kips
o
o
o
18”
24”
24

25. Design for Axial Compression -- Example
Concrete Crushing
A1 = 18 x 18 = 324 in2 (Plan area of base plate)
A2 = (24)(24) = 576 in2 (Plan area of concrete pedestal)
A2/A1 = 576/324 = 1.78 < 4
o
o
o
24”
= 0.65 (0.85 × 3.0 ) (324 ) 1.78
= 716 k > 250 k OK
o
18”
′
φPp = φ 0.85 f c A 1
A2
A1
18”
24”
25

26. Design for Axial Compression -- Example
Plate Bending
n = 5.82 in. m = 4.38 in.
7.96”
n ′ = (1 / 4 ) db f
= (1 / 4 ) 9 .73 x 7 .96
= 2 .20 in .
 4db f  Pu

X=
2  φP
 (d + b )
f

 p
 4x9.73x7.96  250

=
 (9.73 + 7.96 )2  716 = 0.333


4.38”
9.24”
9.73”
18”
4.38”
5.82 6.37 5.82
18”
26

27. Design for Axial Compression -- Example
Plate Bending
n = 5.82 in. m = 4.38 in.
7.96”
n ′ = (1 / 4 ) db f
= (1 / 4 ) 9 .73 x 7 .96
= 2 .20 in .
 4db f  Pu

X=
2  φP
 (d + b )
f

 p
 4x9.73x7.96  250

=
 (9.73 + 7.96 )2  716 = 0.333


4.38”
9.24”
9.73”
18”
4.38”
5.82 6.37 5.82
18”
27

28. Design for Axial Compression -- Example
Plate Bending
2 X
2 0 . 333
λ =
=
1+ 1-X
1 + 1 - 0 . 333
= 0 . 635 ≤ 1 . 0
λ n ' = 0 . 635 x 2 . 20 = 1 . 40 in .
7.96”
4.38”
9.73”
9.24”
l = max {m, n, λn′}
′
= max {4.38,5.82,1.40} = 5.82 in.
4.38”
fpu = Ru /BN = 250/(18x18)
= 0.772 ksi
18”
5.82 6.37 5.82
18”
28

29. Design for Axial Compression -- Example
Plate Bending
tp =
2f pu l 2
0.9Fy
=
2 x 0.772 x 5.82 2
0.9 x 36
7.96”
4.38”
= 1.27 in . ≤ 1.5in . OK
9.24”
9.73”
18”
4.38”
PL 1-½ x 18 x 1’-6” A36
is Adequate.
5.82 6.37 5.82
18”
29

30. Design for Axial Compression
Variation of φPn with Base Plate Thickness with Increasing Axial Force
φPn
m or n
c
c
c
BN = bfd
Required tp
30

31. Design for Axial Compression
Was the base plate too strong?
31

32. Base Plates for
Axial Tension
32

33. Design for Tensile (Uplift) Forces
Connection Limit States
• Anchor Rod Tensile Strength
• Concrete Pull-out Strength
• Concrete Anchorage Tensile Strength
• Base Plate Bending Strength
33

34. Design for Tensile (Uplift) Forces
Anchor Rod Tensile Strength
• Tensile Strength
φTn = φ FntAb
where φ = 0.75
Fnt = 0.75Fu
Fu = specified minimum tensile strength of anchor rod
= 58 ksi (300 MPa) for Gr 36
= 75 ksi (400 MPa) for Gr 55
= 125 ksi (650 MPa) for Gr 125
Notes: Ab is the nominal area of the anchor rod = πd2/4.
0.75 in 0.75Fu account for rupture (tensile) area.
See AISC 14th Ed. Manual Table 7-17 for actual areas.
34

35. Design for Tensile (Uplift) Forces
Ex.
Determine the design strength,φTn, for the limit state
of anchor rod tension rupture. 4 - ¾ in. (20 mm)
diameter, Grade 36 anchor rods
φTn = 4 x 0.75 (0.75Fu) Ab
= 4 x 0.75 (0.75x58)(π0.752/4)
= 4 x 14.4 kips (4 x 53 kN)
= 57.6 kips (212 kN)
35

36. Design for Tensile (Uplift) Forces
Concrete Pullout Strength
• Provisions in ACI 318-08, Section D5.3
• Design pullout strength of headed anchor
rod or anchor rod with nut:
φNp = φ ψ4Abrg8f’c
where φ = 0.70
ψ4 = 1.4 for no cracking, 1.0 if cracking exists
Abrg = net bearing area of the anchor rod head or nut, in2
f’c = specified compression strength of concrete, psi
Notes: Hooked anchor rods are not recommended with tensile
loadings.
36

37. Design for Tensile (Uplift) Forces
Concrete Pullout Strength
• AISC Design Guide 1 Table for Strengths with Heavy Hex Nuts
Note: kN = 4.448 x kips
N/mm2 = 6.895x10-3 x psi
37

38. Design for Tensile (Uplift) Forces
Concrete Breakout Strength
• Provisions in ACI 318-08, Section D4.2.2
Full breakout cone
Breakout cone for group anchors
Breakout cone near edge
38

39. Design for Tensile (Uplift) Forces
Base Plate Bending Strength
• AISC Design Guide 1 recommended bend lines.
g2
g1
Alternate Critical Section is the
full width of the base plate.
39

40. Design for Tensile (Uplift) Forces
Base Plate Bending Strength
• Other possible bend lines.
Critical
Section
Critical
Section
bf + 1 in.
Similar to Extended End-Plates
For all cases:
Define: x = distance from center of anchor bolt to critical section
w = width of critical section
Tu = force in anchor bolt
4Tu x
t p ,min =
φMn = 0.9Fywtp2/4 = Mu = Tux
0.9Fy w
40

41. Base Plates for Axial
Compression and Moment
41

42. Design for Axial Compression and Moment
Connection Limit States
• Concrete Crushing
• Anchor Rod Tensile Strength
• Concrete Pull-out Strength
O
• Concrete Anchorage Tensile Strength
• Base Plate Bending Strength
Cases
• T = 0 (Relatively small moment)
• T > 0 (Relatively large moment)
42

43. Design for Axial Compression and Moment
Limit for T = 0
∑Fy = 0 with T=0 Base Plate is B by N in plan.
Pr = qY = fpBY
∑Mo = 0
Pre = qY2/2 – PrN/2
Then
e = N/2 – Y/2 of if fp < fp,max
with
′
′
fp ,max = 0.65x0.85fc A 2 / A1 ≤ 0.65x 1.7fc
then
ecrit = N/2 –Pr/(2Bfp,max)
Therefore
If e < ecrit, T =0 and Y = N-2e
ecrit = N/2 –Pr/(2Bfp,max)
43

44. Design for Axial Compression and Moment
For T > 0
e > ecrit and fp = fp,max
∑Fy = 0
Pr – T – fp,maxBY =0
∑Mo = 0
T(N/2+f) + Pr(N/2) – Pre – fp,maxBY2/2 = 0
Solving the resulting quadratic equation
Note: If the quantity in the
radical is less than zero, a
larger base plate is required.
Y =(f + N / 2) − (f +
N 2 2Pr (e + f )
) −
2
fp ,max B
T = fp ,max BY − T
44

45. Design for Axial Compression and Moment
Ex. 1. Determine required plate thickness and anchor rod diameter.
Given: Pu = 376 kips Mu = 940 in-kips
W12x96 A992
N = 19 in. B = 19 in. A2/A1 = 1 < 4 bf = 12.2 in. d = 12.7 in.
fc’ = 4.0 ksi Fy = 36 ksi
f = 8 in.
Solution:
′
fp ,max = 0.65x0.85fc A 2 / A1
= 0.65x0.85x4.0 1.0 = 2.21 ksi
e = Mu/Pu = 970/376 = 2.50
ecrit = N/2 –Pr/(2Bfp,max)
= 19.0/2 – 376/(2x19.0x2.21)
= 5.02 in.
e < ecrit → T = 0 and Y = N-2e = 19.0 – 2x 2.50
= 14.0 in.
45

46. Design for Axial Compression and Moment
Ex. 1. Determine required plate thickness and anchor rod diameter.
Given: Pu = 376 kips Mu = 940 in-kips
W12x96 A992
N = 19 in. B = 19 in. A2/A1 = 1 < 4 bf = 12.2 in. d = 12.7 in.
fc’ = 4.0 ksi Fy = 36 ksi
f = 8 in.
Solution Continued:
fp = Pu/(NY)
= 376/(19.0x14.0) = 1.41 ksi
m = (N-0.95d)/2 = (19.0-0.95x12.7)/2 = 3.47 in.
m = (B-0.80bf)/2 = (19.0-0.80x12.2)/2 = 4.62 in.
tp =
2f pu n 2
0.9Fy
=
2 x1.41x 4.62 2
= 1.36 in .
0.9 x 36
Use PL 1½ x 19 x 1ft 7 in. A36
4 – ¾ in. Anchor Rods x 12 in. F1554 Gr 36
w/ heavy hex nuts at bottom.
46

47. Design for Axial Compression and Moment
Ex. 2. Determine required plate thickness and anchor rod diameter.
Given: Pu = 376 kips Mu = 2500 in-kips
W12x96 A992
N = 19 in. B = 19 in. A2/A1 = 1 < 4 bf = 12.2 in. d = 12.7 in.
fc’ = 4.0 ksi Fy = 36 ksi
f = 8 in.
Solution:
′
fp ,max = 0.65x0.85fc A 2 / A1
= 0.65x0.85x4.0 1.0 = 2.21 ksi
e = Mu/Pu = 2500/376 = 6.65
ecrit = N/2 –Pr/(2Bfp,max)
= 19.0/2 – 376/(2x19.0x2.21)
= 5.02 in.
N
2 P (e + f )
e > ecrit → T > 0 and Y =(f + N / 2) − (f + )2 − r
2
fp ,max B
47

48. Design for Axial Compression and Moment
Ex. 2. Determine required plate thickness and anchor rod diameter.
Given: Pu = 376 kips Mu = 2500 in-kips
W12x96 A992
N = 19 in. B = 19 in. A2/A1 = 1 < 4 bf = 12.2 in. d = 12.7 in.
fc’ = 4.0 ksi Fy = 36 ksi
f = 8 in.
Solution Continued:
N 2 2Pr (e + f )
Y = (f + N / 2 ) − (f + ) −
2
fp ,max B
19.0 2 2x 376(6.65 + 8.0)
) −
= (8.0 + 19.0 / 2) − (8.0 +
2
2.21x19.0
= 10.9 in.
fp = Pu/(NY)
= 376/(19.0x10.9) = 1.82 ksi
48

49. Design for Axial Compression and Moment
Ex. 2. Determine required plate thickness and anchor rod diameter.
Given: Pu = 376 kips Mu = 2500 in-kips
W12x96 A992
N = 19 in. B = 19 in. A2/A1 = 1 < 4 bf = 12.2 in. d = 12.7 in.
fc’ = 4.0 ksi Fy = 36 ksi
f = 8 in.
Solution Continued:
m = (N - 0.95d)/2 = (19.0-0.95x12.7)/2 = 3.47 in.
n = (B - 0.80bf)/2 =(19.0-0.80x12.2)/2 = 4.62 in.
tp =
2f pu m 2
0.9Fy
=
2 x1.82 x 4.62 2
= 1.54 in .
0.9 x 36
Need to check tensions side.
49

50. Design for Axial Compression and Moment
Ex. 2. Determine required plate thickness and anchor rod diameter.
Given: Pu = 376 kips Mu = 2500 in-kips
W12x96 A992
N = 19 in. B = 19 in. A2/A1 = 1 < 4 bf = 12.2 in. d = 12.7 in.
fc’ = 4.0 ksi Fy = 36 ksi
f = 8 in.
Solution Continued:
T = fp,max BY – Pu
= 2.21x19.0x10.9 – 376 = 80.4 kips
Try 2 – Anchor Rods each Side
Required plate thickness:
X = f – 0.95d/2 = 8.0 -0.95x12.7/2
= 1.96 in.
x
w = bf + 1.0 = 12.2 + 1.0 = 13.0 in.
f
4T x
4 x 80 .4 x1.96
t p ,min =
=
= 1.22 in .
0.9Fy w
0.9 x 36 x13 .0
Use PL 1½ x 19 x 1ft 7 in. A36 50

51. Design for Axial Compression and Moment
Ex. 2. Determine required plate thickness and anchor rod diameter.
Given: Pu = 376 kips Mu = 2500 in-kips
W12x96 A992
N = 19 in. B = 19 in. A2/A1 = 1 < 4 bf = 12.2 in. d = 12.7 in.
fc’ = 4.0 ksi Fy = 36 ksi
f = 8 in.
Solution Continued:
Trod = 80.4/2 = 40.2 kips per anchor rod
Try 1 -1/4 in. diameter
φTn = 0.75 (0.75Fu) Ab
= 0.75 (0.75x58)(π1.252/4)
= 40.0 kips ≈ 40.2 kips Say OK
Check Pullout:
From AISC Design Guide 1, Table 3.2, φTn = 50.2 kips OK
51

52. Shear Anchorage
of Base Plates
52

53. Shear Anchorage of Base Plates
Transferring Shear Forces (ACI 318-08 and ACI 349-06)
• Friction between base plate and grout or concrete surface.
φVn = φμPu < φ0.2fc’Ac or φ800Ac
where φ = 0.75
μ = coefficient of friction = 0.4
Pu = factored compressive axial force
Ac = plan area of base plate, BN
• Bearing of the column and base plate and/or shear lug against
concrete.
φPu,brg = 0.55fc’Abrg
where Abrg = vertical bearing area
53

54. Shear Anchorage of Base Plates
Transferring Shear Forces (ACI 318-08 and ACI 349-06)
• Shear strength of the anchor rods.
Not recommended because of oversize holes in base plate.
• Hairpins and Tie Rods
54

55. Column Erection
Procedures
55

56. Column Erection Procedures
Anchor rods are positioned and placed in the concrete before it
cures. Plastic caps are placed over the anchor bolts to protect
laborers.
56

57. Column Erection Procedures
Concrete block-outs may be made so that the base plate and
anchor bolts are recessed below floor level for safety and
aesthetics.
57

58. Column Erection Procedures
Slotted holes are allow for difference in standard field tolerances
between concrete and steel.
58

59. Column Erection Procedures
The column is leveled by adjusting the anchor bolt nuts below the
plate. Grout will be placed under and around the base plate to
transfer axial forces to the concrete below.
59

60. Column Erection Procedures
Grout will be placed under and around the base plate to transfer
axial forces to the concrete below. At least it should be.
60

61. 61

62. Result of Poor
Anchor Rod Placement
The following slides are courtesy of Fisher &
Kloiber- AISC Field Fixes presentation.
62

63. Anchor Rod Placement
Anchor rods in the wrong location.
63

64. Anchor Rod Placement
Anchor rods in the wrong location.
64

65. Anchor Rod Placement
Anchor rods in the wrong location.
65

66. Anchor Rod Placement
Anchor rods too short.
66

67. Anchor Rod Placement
Anchor rods too long.
67

68. Anchor Rod Placement
Shop rework fo column and base plate.
68

69. Anchor Rod Placement
Anchor rods
69

70. Poor Anchor Rod Placement
Anchor bolts run over by a crane.
70

71. Poor Anchor Rod Placement
Anchor bolts run over by something.
71

72. Our next IMCA Manual, due to come out shortly, will state in the Code
of Standard Practice, that in addition to the requirement that the
contractor responsible for placing the anchors in site, present a drawing
showing the as-placed location of the anchors, that the supplier of the
structure provide the necessary templates for this purpose. They are to be
so designed as to insure the correct position, both vertically (including
the length of the anchor extending above the concrete surface) and
horizontally, show the location of the building axis relative to the anchor
group and leave permanent marks of the axis in the concrete surface. The
price of the templates is recommended to be the average price of the steel
structure. (We save so much on the cost of erection that we would be glad to
give the templates away free, but don't tell my clients.)
We have been using this method over the past 5 years in all
of our jobs. We are delighted in not having had a single problem in placing
the columns, the structures are all self-plumbing, the bolts all easily
inserted and the time for erection greatly shortened. On a job we are now
doing, from the date our bid was accepted, it took 7 weeks to design,
fabricate, erect the steel structure and install 20,000 sq. ft. of decking,
with shear anchors hand welded, for a three story school building, working
one 11 hr shift both at the shop and the site. A second similar 30,000
sq. ft. building will be finished this week, 8 weeks after the first one.
72

73. 73

74. 74

75. 75

76. 76

77. 77

78. 78

79. 79

80. 80

81. 81

82. 82

83. 83