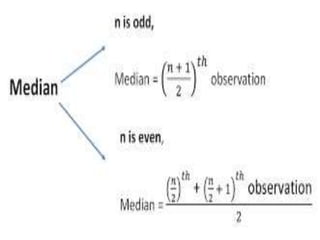
This document discusses various statistical parameters used in pharmaceutical research and development. It describes parameters like measures of central tendency (mean, median, mode), dispersion (variance, standard deviation), coefficient of dispersion, residuals, factor analysis, absolute error, mean absolute error, and percentage error of estimate. Measures of central tendency provide a summary of the central or typical values in a data set. Dispersion measures provide a way to quantify how spread out the data is from the central value. Other parameters like residuals, errors, and factor analysis are used to analyze relationships in complex data.

1. STATISTICAL PARAMETERS
BY
HASIFUL ARABI J
DEPT.OF PHARMACEUTICS

2. STATISTICAL PARAMETERS INVOLVED IN
PHRMACEUTICAL RESEARCH &DEVELOPMENT
Statistics:
Statistics is an important tool in pharmacological
research that is used to summarize (descriptive
statistics) experimental data in terms of central
tendency (mean or median) and variance (standard
deviation, standard error of the mean, confidence
interval or range) but more importantly it enables us to
conduct hypothesis testing

3. CONTD….
Parameters:
A parameter is something in an equation that is
passed on in an equation. It means something
different in statistics. It’s a value that tells you
something about a population and is the opposite
from a statistic, which tells you something about
a small part of the population.

4. STATISTICAL PARAMETERS
The various statistical parameters are,
1. Measures of central tendency
2. Dispersion (also called Variability, Scatter, Spread)
3. Coefficient of Dispersion (COD)
4. Variance
5. Standard Deviation (SD) σ
6. Residuals
7. Factor Analysis
8. Absolute Error (AE)
9. Mean Absolute Error (MAE)
10. Percentage Error of Estimate (PE)

5. 1. MEASURES OF CENTRAL TENDENCY:
• Measures of central tendency are also usually called
as the averages.
• They give us an idea about the concentration of the
values in the central part of the distribution.
• The following are the five measures of central
tendency that are in common use:
(i) Arithmetic mean,
(ii) Median,
(iii) Mode

6. CONTD….
• MEAN: The average of the data
• MEDIAN: The middle value of the data
• MODE: Most commonly occurring value

7. Mean (Average)
• Mean locate the centre of distribution. Also known
as arithmetic mean Most Common Measure The
mean is simply the sum of the values divided by the
total number of items in the set. Affected by Extreme
Values.

8. Median:
• The median is determined by sorting the data set
from lowest to highest values and taking the data
point in the middle of the sequence.
• Middle Value In Ordered Sequence
• If Odd n, Middle Value of Sequence
• If Even n, Average of 2 Middle Value
• Not Affected by Extreme Values

10. Mode
• Measure of Central Tendency
• The mode is the most frequently occurring value in
the data set.
• May Be No Mode or Several Modes
• Mode is readily comprehensible and easy to
calculate.
• Mode is not at all affected by extreme values.
• Mode can be conveniently located even if the
frequency distribution has class intervals of unequal
magnitude

11. 2. Dispersion (also called Variability, Scatter,
Spread)
• It is the extent to which a distribution is stretched or
squeezed.
• Common examples of Statistical Dispersion are the variance,
standard deviation and interquartile range.
3. Coefficient of Dispersion (COD)
• It is a measure of spread that describes the amount of
variability relative to the mean and it is unit less.
𝑪𝑶𝑫 = 𝝈/ 𝝁 ∗ 𝟏𝟎𝟎

12. 4. Variance
• It is the expectation of the squared deviation of a
random variable from its mean and it informally
measures how far a set of random numbers are
spread out from the mean.
• It is calculated by taking the differences between
each number in the set and the mean, squaring the
differences (to make them positive) and diving the
sum of the squares by the number of values in the
set.

13. • The variance provides the user with a
numerical measure of the scatter of the data.

14. 5. Standard Deviation (SD) σ
• It is a measure used to quantify the amount of variation or
dispersion of a set of data values.
• It is a number that tells how measurement for a group are
spread out from the average (mean) or expected value.
• A low standard deviation means most of the numbers are
very close to the average while a high value indicates the data
to be spread out.
• The SD provides the user with a numerical measure of the
scatter of the data.

15. 6. Residuals
• It is the difference between the observed value of
the dependent variable (y) and the predicted value
(y’).
• Each data point has one residual. Both the sum and
the mean of the residuals are equal to zero.
𝑹 = 𝑶𝒃𝒔𝒆𝒓𝒗𝒆𝒅 𝒀 𝒗𝒂𝒍𝒖𝒆 − 𝑷𝒓𝒆𝒅𝒊𝒄𝒕𝒆𝒅 𝒀 𝒗𝒂𝒍𝒖𝒆

16. 7. Factor Analysis
• It is a useful tool for investigating variable
relationships for complex concepts allowing
researchers to investigate concepts that are not
easily measured directly by collapsing a large number
of variables into a few interpretable underlying
factors.

17. 8. Absolute Error (AE)
• It is the magnitude of the difference between the
exact value and the approximation.
• The relative error is the absolute error divided by
the magnitude of the exact value.
𝑨𝑬 = 𝑿 𝒎𝒆𝒂𝒔𝒖𝒓𝒆𝒅 − 𝑿 𝒂𝒄𝒕𝒖𝒂𝒍

18. 9.Mean Absolute Error (MAE)
• It is a quantity to measure how close forecasts or
predictions are to the eventual outcomes.
• It is an average of the absolute errors.
• The simplest measure of forecast accuracy is MAE.
• The relative size of error is not always obvious.

19. 10. Percentage Error of Estimate (PE)
• It is the difference between the approximate
and the exact values as a percentage of the
exact value.
%𝑬𝒓𝒓𝒐𝒓 = 𝑬𝒙𝒂𝒄𝒕 𝑽𝒂𝒍𝒖𝒆 − 𝑨𝒑𝒑𝒓𝒐𝒙𝒊𝒎𝒂𝒕𝒆
𝑽𝒂𝒍𝒖𝒆 𝑬𝒙𝒂𝒄𝒕 𝑽𝒂𝒍𝒖𝒆 ∗ 𝟏𝟎𝟎