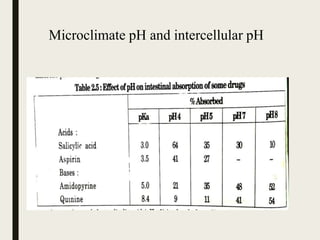
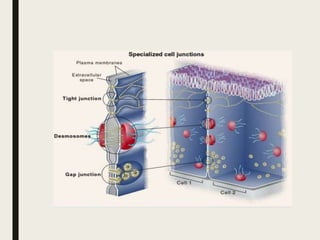
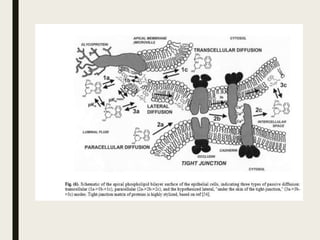
The document discusses several key concepts related to drug transport and absorption: 1) The pH partition hypothesis states that acidic drugs are absorbed from acidic solutions and basic drugs from alkaline solutions, though some exceptions exist due to the microclimate pH near the membrane surface. 2) Tight junctions form a virtually impermeable barrier between cells, composed of sealing strands that prevent fluid passage. 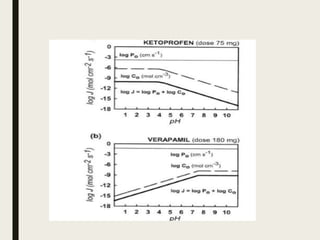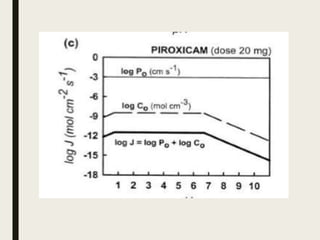3) According to Fick's first law, passive diffusion of solutes is determined by concentration gradients and membrane permeability. For ionizable drugs, the uncharged form is more permeable. The pH partition hypothesis relates permeability to pH and the fraction of uncharged molecules.

1. TRANSPORT MODELS
Presented By
Sujitha Mary
M Pharm
St Joseph College Of Pharmacy

2. Microclimate pH and intercellular pH

3. • According to pH partition hypothesis, acidic drugs absorbed
from acidic solution and basic drugs absorbed from alkaline
solution.
• Some deviations are observed, Salicylic acid ,aspirin are
completely ionised in buffer solution and rapidly absorbed . To
explain these exceptions there exist a virtual membrane pH on
the surface of the absorbing membrane.
• pH determines the fraction of unionised form of drug.
• Effective pH at the surface of the intestinal membrane, different
from the pH of the solution in the lumen and it is well absorbed.

4. • This is because the membrane surface is negatively
charged with the polyanionic chains, which attract
hydrogen ions and accumulation of H+ ions near
membrane cause decrease in pH . The pH at this virtual
surface or microclimate near the membrane determines
degree of ionisation.
• The unionized form of drug in solution would be readily
absorbed than ionized form.

5. TIGHT JUNCTION COMPLEX
• Tightjunctions,also known asoccludingjunctions
• The closely associatedareasof two cells whose membranes join
together forming avirtually impermeable barrier to fluid.
• Tight junctions are composed of abranching network of
sealing strands, eachstrand acting independently from the
others. Therefore, the efficiency of the junction in
preventing ion passageincreases exponentially with the
number of strands. Eachstrand is formed from a row of
transmembrane proteins.

7. • Freeze-fracture electron micrographs of the constrictive region
of the TJ show netlike arrays of strands circumscribing the
cell, forming a division between the apical and the basolateral
sides.
• A region ten strands wide forms junctions that have very small
pore openings; fewer strands produce leakier junctions. The
actual cell-cell adhesions occur in the adheren junctions,
located further away from the apical side.
• Apparently three calciums contiguously link 10-residue
portions of cadheren proteins spanning from two adjoining cell
walls, Calcium-binding agents can open the junctions by
interactions with the cadheren complex.

9. Permeability-Solubility-Charge State and the
pH Partition Hypothesis
 According to Ficks first law passive diffusion of a solute
is the product of diffusivity and concentration gradient of
the solute inside the membrane.
 The membrane/water apparent partition coefficient
relates the latter internal gradient to the external bulk-
water concentration difference between the two solutions
separated by the membrane

10. For an ionizable molecule to permeate by passive diffusion
most efficiently, the molecule needs to be in its uncharged
form at the membrane surface.
The amount of the uncharged form present at a given pH,
which directly contributes to the flux, depends on several
important factors, such as pH, binding to proteins and bile
acids, self-binding, and solubility

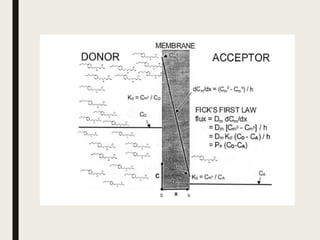
12. Consider a vessel is divided into 2 chambers separated by lipid
membrane ,left side is the donor compartment and right side is
the acceptor compartment.
Fick’s first law applied to homogeneous membranes at steady
state is a transport equation,
J = Dm dCm/dx = Dm [ Cm0 - Cmh ] / h
J = flux
Cm0 – Cmh = uncharged form of solute
within the membrane at two membrane boundaries
h = thickness of the membrane
Dm = diffusivity of the solute within the
membrane
At steady state, the concentration gradient, dCm/dx, within the
membrane is linear

13. The limitation of eq. 1 is that measurement of concentrations of
solute within different parts of the membrane is very inconvenient.
So we can estimate the distribution coefficients between bulk
water and the membrane, log Kd (the pH dependent apparent
partition coefficient),
we can convert eq. 1 into a more accessible form,
J = Dm Kd (CD - CA) / h (2)
where the substitution of Kd allows us to use bulk water
concentrations in the donor and acceptor compartments, CD and
CA, respectively. ( for ionizable molecules, CA and CD refer to
the concentrations of the solute summed over all forms of charge
state.)

14. Eq. 2 is still not sufficiently convenient, since we need to
estimate Dm and Kd.
 It is a common practice to lump these parameters and the
thickness of the membrane into a composite parameter, called
“effective permeability,” Pe,
Pe = Dm Kd / h (3)
The relevance of eq. 2 (which predicts how quickly molecules
pass through simple membranes) to solubility comes in the
concentration terms.
Consider “sink” conditions, where CA is essentially
zero. Eq. 2 reduces to the following flux equation
J = Pe CD (4)

15. Flux depends on the product of effective permeability of the
solute times the concentration of the solute (summed over all
charge state forms) at the water-side of the donor surface of
the membrane.
 This concentration ideally may be equal to the dose of the
drug, unless the dose exceeds the solubility limit, in which
case it is equal to the solubility.
 Since the uncharged molecular species is the permeant, eq.
4 may be restated as
J = Po Co < Po So (5)

16. Where, Po = the intrinsic permeability
Co = concentration of the uncharged species,
respectively.
The intrinsic permeability does not depend on
pH, but its cofactor in the flux equation, Co, does. The
concentration of the uncharged species is always equal to
or less than the intrinsic solubility of the species, So.
Note that for the uncharged species, eq. 3 takes on the
form
Po = Dm Kp / h (6)
where Kp = Cm(0) / CDo; also, Kp = Cm(h) / CAo;
CDo and CAo are the aqueous solution concentrations of
the uncharged species in the donor and acceptor sides,
respectively.

19. REFERENCE
1.Fundamentals of Biopharmaceutics and
pharmacokinetics by V.Venkateswarlu,page no:
25
2.Biopharmaceutics and Pharmacokinetics by
page no:2.8
3.Absorption and drug development solubility
permeability charge state by Alex Avdeef