Recommended
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
東京都市大学 データ解析入門 4 スパース性と圧縮センシング1
PDF
PDF
文字列カーネルによる辞書なしツイート分類 〜文字列カーネル入門〜
PPTX
【DL輪読会】Spectral Normalisation for Deep Reinforcement Learning: An Optimisatio...
PPTX
PPTX
2014.01.23 prml勉強会4.2確率的生成モデル
ZIP
PDF
PDF
PDF
[DL輪読会]Control as Inferenceと発展
PDF
Control as Inference (強化学習とベイズ統計)
PDF
PDF
PDF
PPTX
猫でも分かるVariational AutoEncoder
PDF
PPTX
【DL輪読会】Hopfield network 関連研究について
PDF
画像局所特徴量と特定物体認識 - SIFTと最近のアプローチ -
PPTX
PDF
More Related Content What's hot
PDF
PDF
PDF
東京都市大学 データ解析入門 4 スパース性と圧縮センシング1
PDF
PDF
文字列カーネルによる辞書なしツイート分類 〜文字列カーネル入門〜
PPTX
【DL輪読会】Spectral Normalisation for Deep Reinforcement Learning: An Optimisatio...
PPTX
PPTX
2014.01.23 prml勉強会4.2確率的生成モデル
ZIP
PDF
PDF
PDF
[DL輪読会]Control as Inferenceと発展
PDF
Control as Inference (強化学習とベイズ統計)
PDF
PDF
PDF
PPTX
猫でも分かるVariational AutoEncoder
PDF
PPTX
【DL輪読会】Hopfield network 関連研究について
PDF
画像局所特徴量と特定物体認識 - SIFTと最近のアプローチ -
Similar to ディジタル信号処理 課題解説 その5
PPTX
PDF
PDF
ディジタル信号処理 課題解説(その1) 2014年度版
PPTX
Graph convolution (スペクトルアプローチ)
PDF
PDF
ディジタル信号処理 課題解説(その3) 2014年度版
PDF
2021年度秋学期 画像情報処理 第3回 フーリエ級数とフーリエ変換 (2021. 10. 8)
PDF
2022年度秋学期 画像情報処理 第3回 フーリエ級数とフーリエ変換 (2022. 10. 7)
PPTX
PDF
PDF
PDF
2020年度秋学期 画像情報処理 第3回 フーリエ変換とサンプリング定理 (2020. 10. 9)
PPTX
音楽信号処理における基本周波数推定を応用した心拍信号解析
PDF
PDF
2014年度春学期 画像情報処理 第4回 離散フーリエ変換 (2014. 5. 7)
PDF
2014年度春学期 画像情報処理 第3回 フーリエ変換とサンプリング定理 (2014. 4.23)
PDF
2015年度春学期 画像情報処理 第4回 離散フーリエ変換 (2015. 4.30)
PDF
2013年度春学期 画像情報処理 第3回「フーリエ変換とサンプリング定理」
PDF
PDF
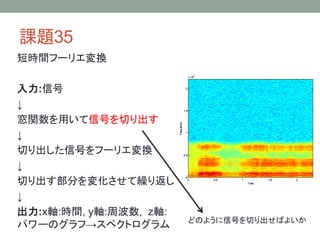
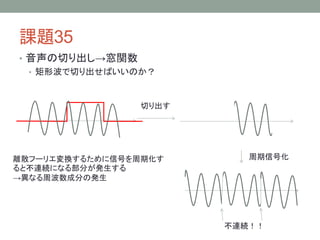
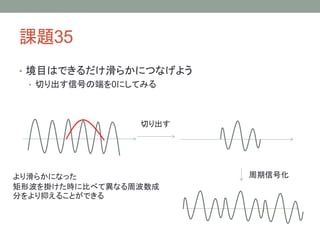
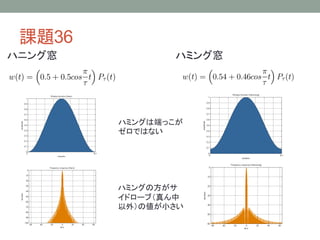
ディジタル信号処理 課題解説 その5 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 課題36
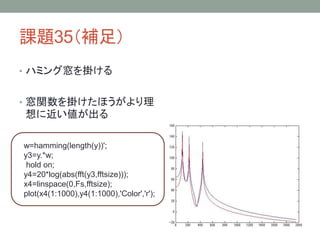
• 2次元の窓関数を作る関数を作成する
function w2=mado2(N,c)
if strcmp(c,'hamming')==1
w=hamming(N);
elseif strcmp(c,'hanning')==1
w=hanning(N);
end
w2=zeros(N,N);
for x=1:N
for y=1:N
r=round(sqrt((x-floor(N/2))^2+(y-floor(N/2))^2))+floor(N/2);
if(r<=N)
w2(x,y)=w(r);
end
end
end
15. 課題36
• 2次元の窓関数を作る関数を作成する
• 自分で関数を定義できる
• 作成したい関数名と同じファイル名でスクリプ
function w2=mado2(N,c)
if strcmp(c,'hamming')==1
w=hamming(N);
elseif strcmp(c,'hanning')==1
w=hanning(N);
end
ここでは窓の大きさNとハミングかハ
ニングかの指定cを入力として2次元
の窓関数w2を出力する
トを作成
• 一行目に
function [ output ]= function_name( input )
と記述すれば,input(入力) を受け取り
output(出力) を返す関数を定義可能
• 複数の入出力が可能
cにhammingという文字列が代入されてい
れば一次元大きさNのハミング窓を,
hanningという文字列が代入されていれば
一次元の大きさNのハニング窓を作成する
16. 課題36
• 2次元の窓関数を作る関数を作成する
w2=zeros(N,N);
for x=1:N
for y=1:N
r=round(sqrt((x-floor(N/2))^2+…
(y-floor(N/2))^2))+floor(N/2);
if(r<=N)
w2(x,y)=w(r);
end
end
end
一次元の窓関数𝑤1(𝑟)から2次元の窓関数
𝑤2(𝑥, 𝑦)を以下の式で作成する
w2 x, y = w1( 𝑥 2 + 𝑦 2 )
ただし窓関数の中央部を原点に移動させる必要
がある
rがNより大きい部分は全て0にする
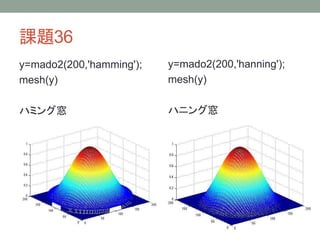
17. 18. 19. 課題36
img=imread('sima.jpg');
img=rgb2gray(img);
w1=mado2(size(img,1),'hanning');
xhan=double(img).*w1;
yhan=fft2(xhan);
詳しい解説は
MATLAB演習の
レンガのパワースペクトル
の部分を参照
[h, w]=size(img);
nw=floor(w/2);
nh=floor(h/2);
imout=[yhan(nh+1:h,nw+1:w),yhan(nh+1:h,1:nw);[yhan(1:nh,nw+1:w),y
han(1:nh,1:nw)]];
imshow(20*log10(abs(imout)),[0 255]);
20. 21. 22. 課題37
𝜓 𝑡 = 𝑔 𝜎 (𝑡)(𝑒
∞
−∞
𝑗𝜔𝑡
− 𝑒
− 𝜎𝜔 2
)のとき
𝜓 𝑡 𝑑𝑡 = 0を確認しなさい
23. 課題37
• 課題8と同じ
(t )dt
1
2
e
t2
4 2
e
jt
e ( ) dt
2
ガウス関数の無限積分
e
x2
dx
( t 2 j t )
t
2
2 2
2
1 4 2
( )
4
e
dt e
e
e dt
2
1
2 2
2
( ) 2
e
4 e
4 2 0
2
2
2
2
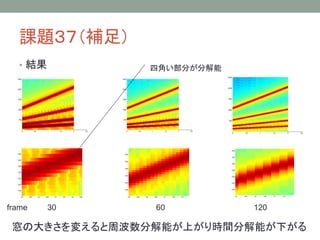
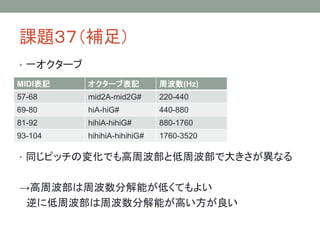
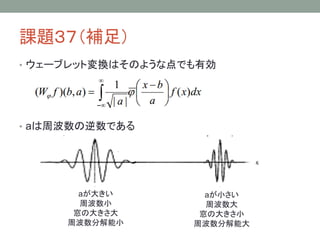
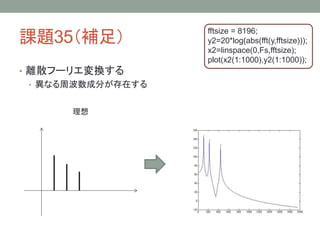
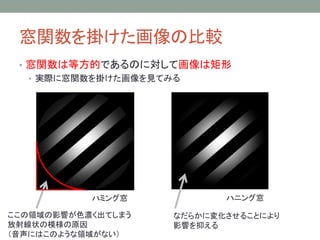
24. 課題37(補足)
分解能とウェーブレット
今度はドレミファソラシドと変化していく音源のスペクトログラム
を求めてみる(またsound(x,fp);で聴いてみよう!!)
fs=16000; %サンプリング周波数
T=2; %音の時間
t=0:1/fs:T; %x軸
f0=130.8;
f1=261.6;
x=0.5*chirp(t,f0,T,f1)+0.25*chirp(t,2*f0,T,2*f1)+...
0.125*chirp(t,4*f0,T,4*f1)+0.125*chirp(t,8*f0,T,8*f1);
x=x.';
25. 課題37(補足)
• スペクトログラムを作成する
frameMs=30;
periodMs=10;
frame=round(fs*frameMs/1000);
period=round(fs*periodMs/1000);
fftlength=2^ceil(log2(frame));
range=1:period:(length(x)-frame);
spec=zeros(fftlength/2+1,length(range));
for ii=1:length(range)
temp=20*log10(abs(fft(x([1:frame]+(ii-1)*period).*blackman(frame),fftlength))+eps);
spec(:,ii)=temp(1:fftlength/2+1);
end
xx=linspace(0,length(x)/fs,size(spec,2));
yy=linspace(0,fs/2,size(spec,1));
surface(xx,yy,spec);shading flat;
ylim([1 2500]);
26. 27. 28. 29. 課題38
𝑑 2 𝑓 𝑡 ∗𝑔 𝑡
𝑑𝑡 2
= 𝑓 𝑡 ∗
𝑑2 𝑔 𝑡
𝑑𝑡 2
が成り立つことを証明し
𝑔 𝑡 =
d2 g t
dt2
1
𝜎 2𝜋
𝑒
𝑡2
− 2
2𝜎
のとき
を計算しなさい
30. 課題38
前半
d 2 f (t ) * g (t ) d 2
2
2
dt
dt
f ( ) g (t )d
二次微分を積分の中へ
d2
d 2 g (t )
f ( ) 2 g (t )d f (t ) *
dt
dt 2
証明終わり
後半
2
2
t 2
dg (t )
1
1
t 2t 2
2 e
3
te 2
dt
なので、
2
2
d 2 g (t )
1
3
dt
2
2
t 2t22
1
2t 2
2e
t 3
1 e
2
t2
2t22
2 1e
31.







![課題36
• 2次元の窓関数を作る関数を作成する
• 自分で関数を定義できる
• 作成したい関数名と同じファイル名でスクリプ
function w2=mado2(N,c)
if strcmp(c,'hamming')==1
w=hamming(N);
elseif strcmp(c,'hanning')==1
w=hanning(N);
end
ここでは窓の大きさNとハミングかハ
ニングかの指定cを入力として2次元
の窓関数w2を出力する
トを作成
• 一行目に
function [ output ]= function_name( input )
と記述すれば,input(入力) を受け取り
output(出力) を返す関数を定義可能
• 複数の入出力が可能
cにhammingという文字列が代入されてい
れば一次元大きさNのハミング窓を,
hanningという文字列が代入されていれば
一次元の大きさNのハニング窓を作成する](https://image.slidesharecdn.com/random-131212214741-phpapp01/85/5-15-320.jpg)


![課題36
img=imread('sima.jpg');
img=rgb2gray(img);
w1=mado2(size(img,1),'hanning');
xhan=double(img).*w1;
yhan=fft2(xhan);
詳しい解説は
MATLAB演習の
レンガのパワースペクトル
の部分を参照
[h, w]=size(img);
nw=floor(w/2);
nh=floor(h/2);
imout=[yhan(nh+1:h,nw+1:w),yhan(nh+1:h,1:nw);[yhan(1:nh,nw+1:w),y
han(1:nh,1:nw)]];
imshow(20*log10(abs(imout)),[0 255]);](https://image.slidesharecdn.com/random-131212214741-phpapp01/85/5-19-320.jpg)




![課題37(補足)
• スペクトログラムを作成する
frameMs=30;
periodMs=10;
frame=round(fs*frameMs/1000);
period=round(fs*periodMs/1000);
fftlength=2^ceil(log2(frame));
range=1:period:(length(x)-frame);
spec=zeros(fftlength/2+1,length(range));
for ii=1:length(range)
temp=20*log10(abs(fft(x([1:frame]+(ii-1)*period).*blackman(frame),fftlength))+eps);
spec(:,ii)=temp(1:fftlength/2+1);
end
xx=linspace(0,length(x)/fs,size(spec,2));
yy=linspace(0,fs/2,size(spec,1));
surface(xx,yy,spec);shading flat;
ylim([1 2500]);](https://image.slidesharecdn.com/random-131212214741-phpapp01/85/5-25-320.jpg)