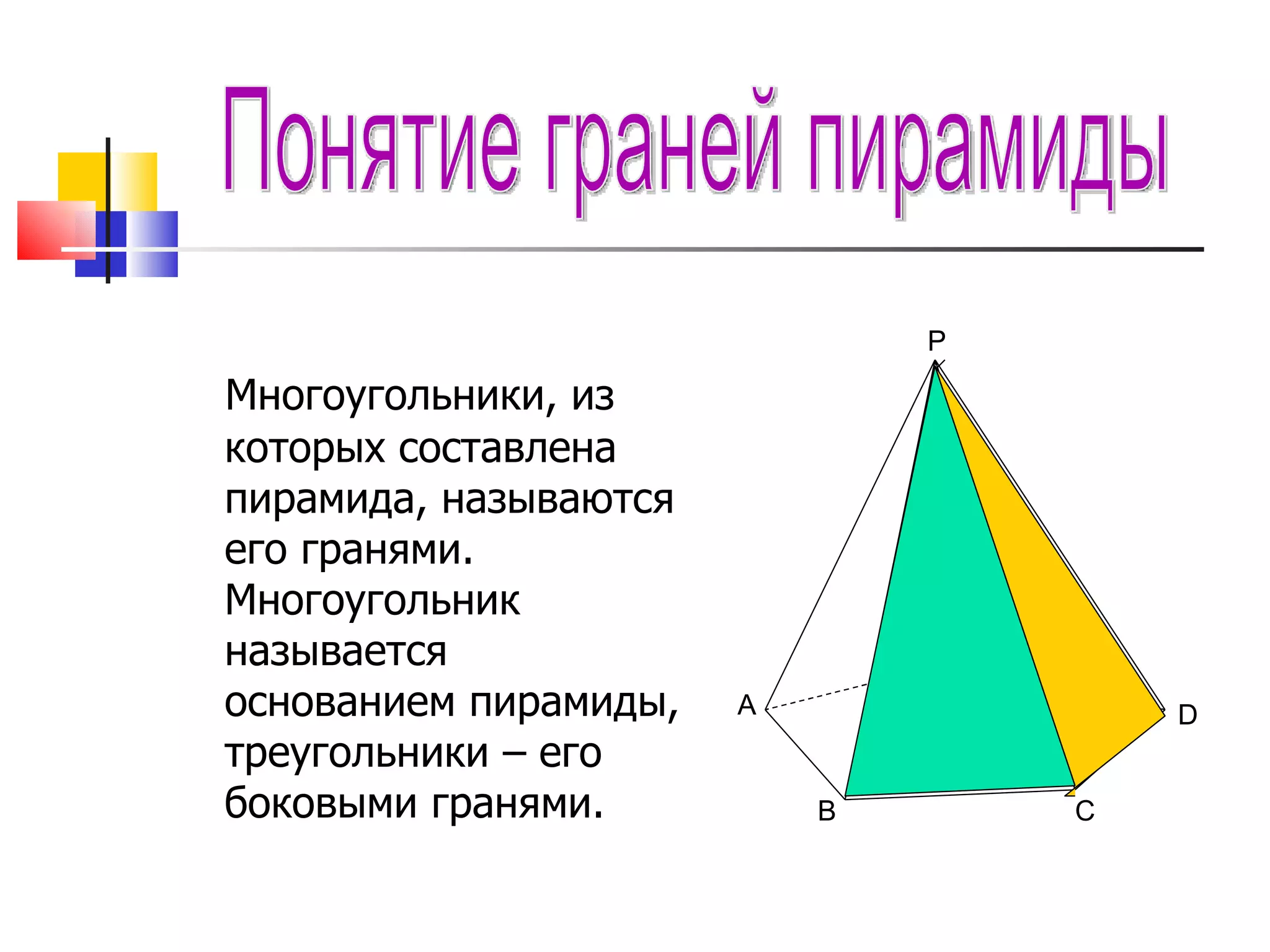
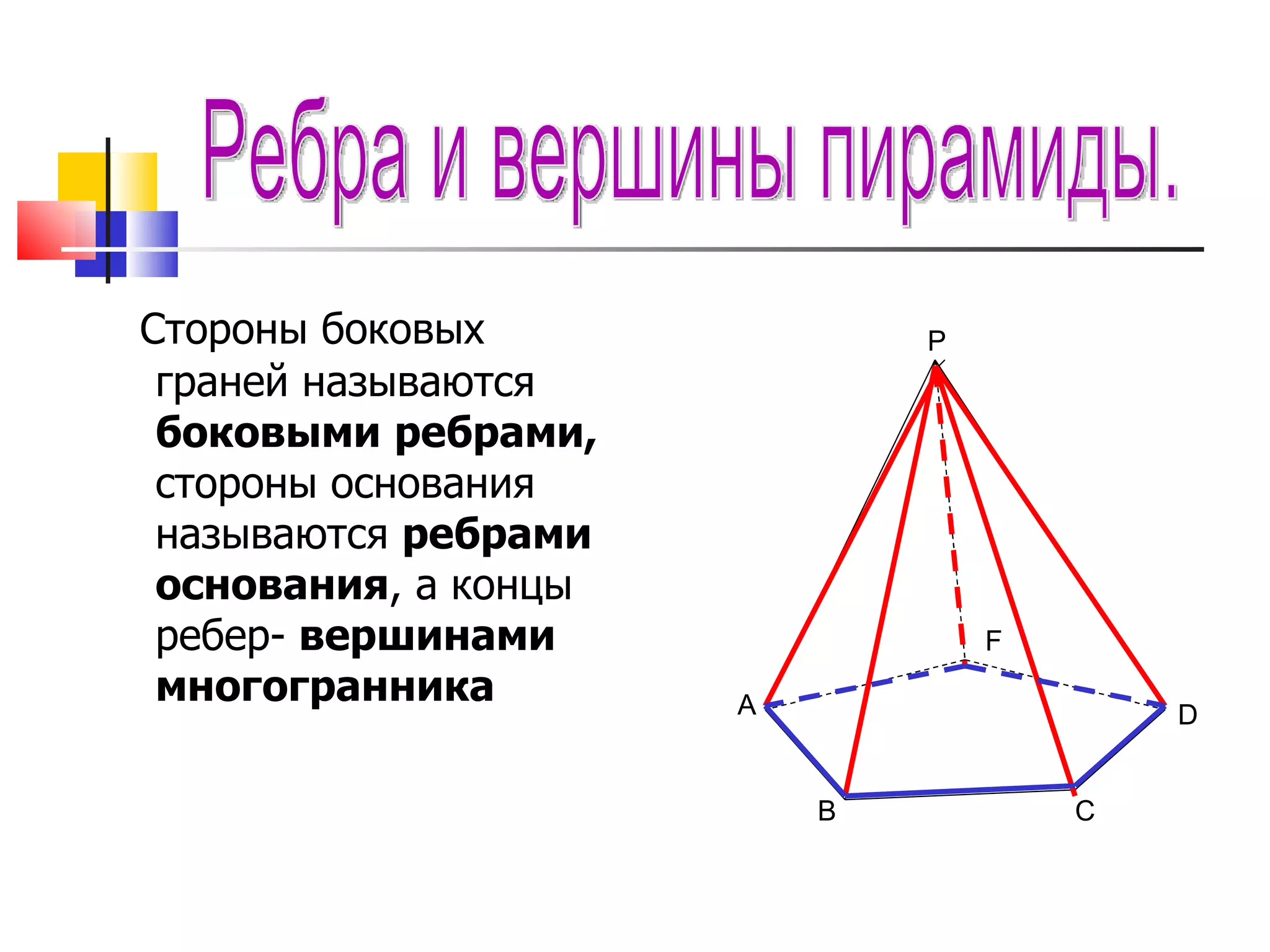
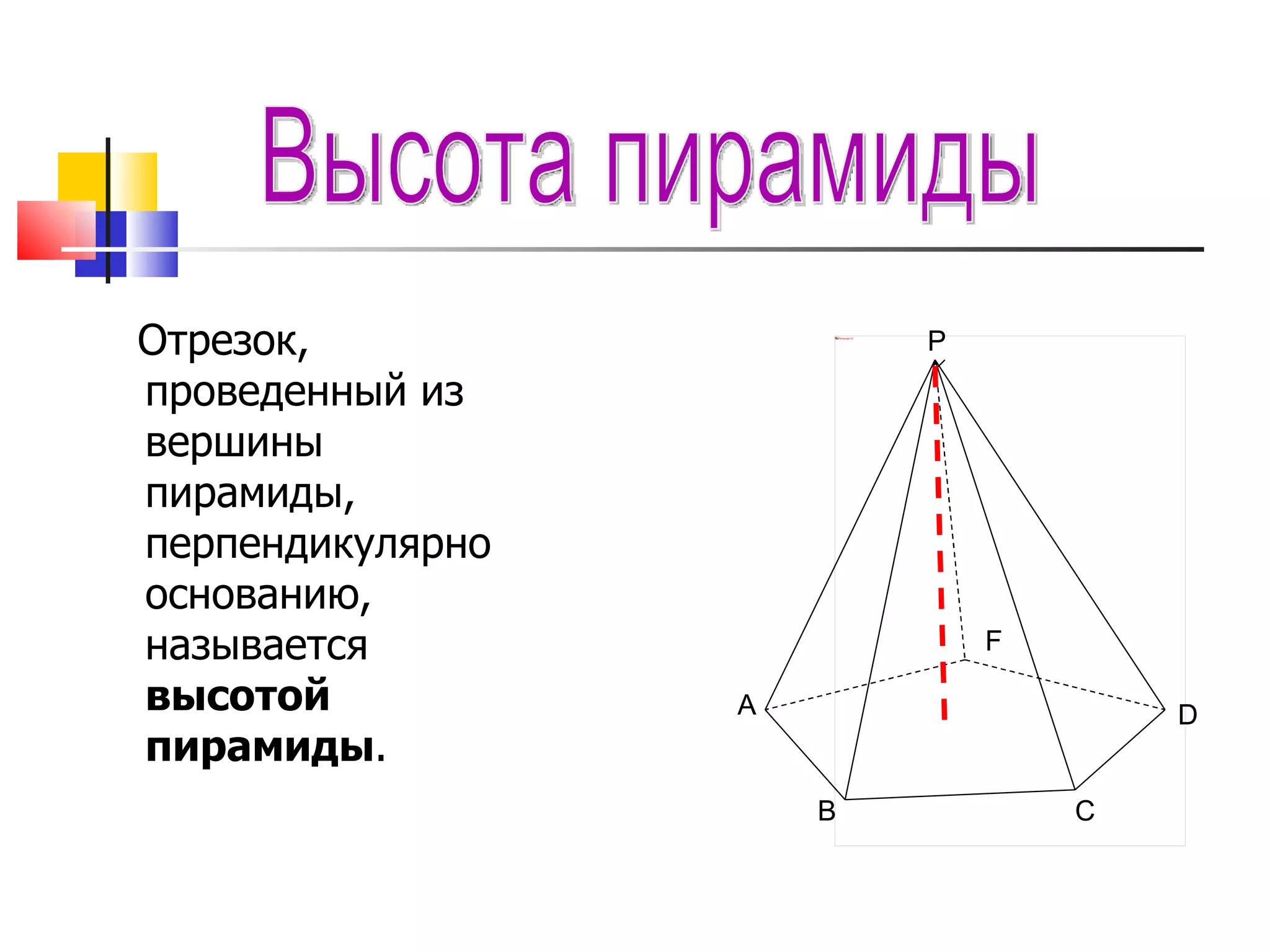
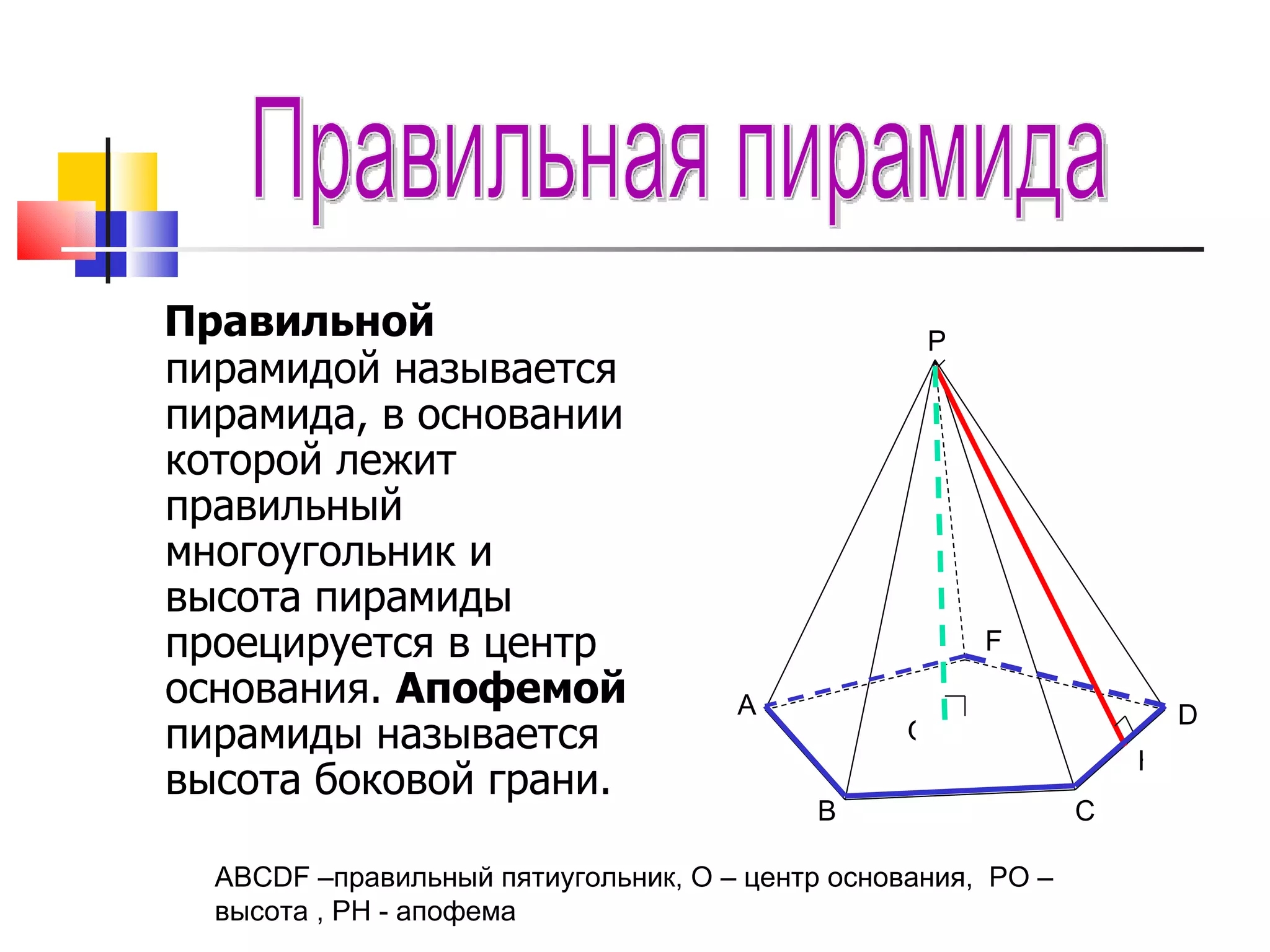
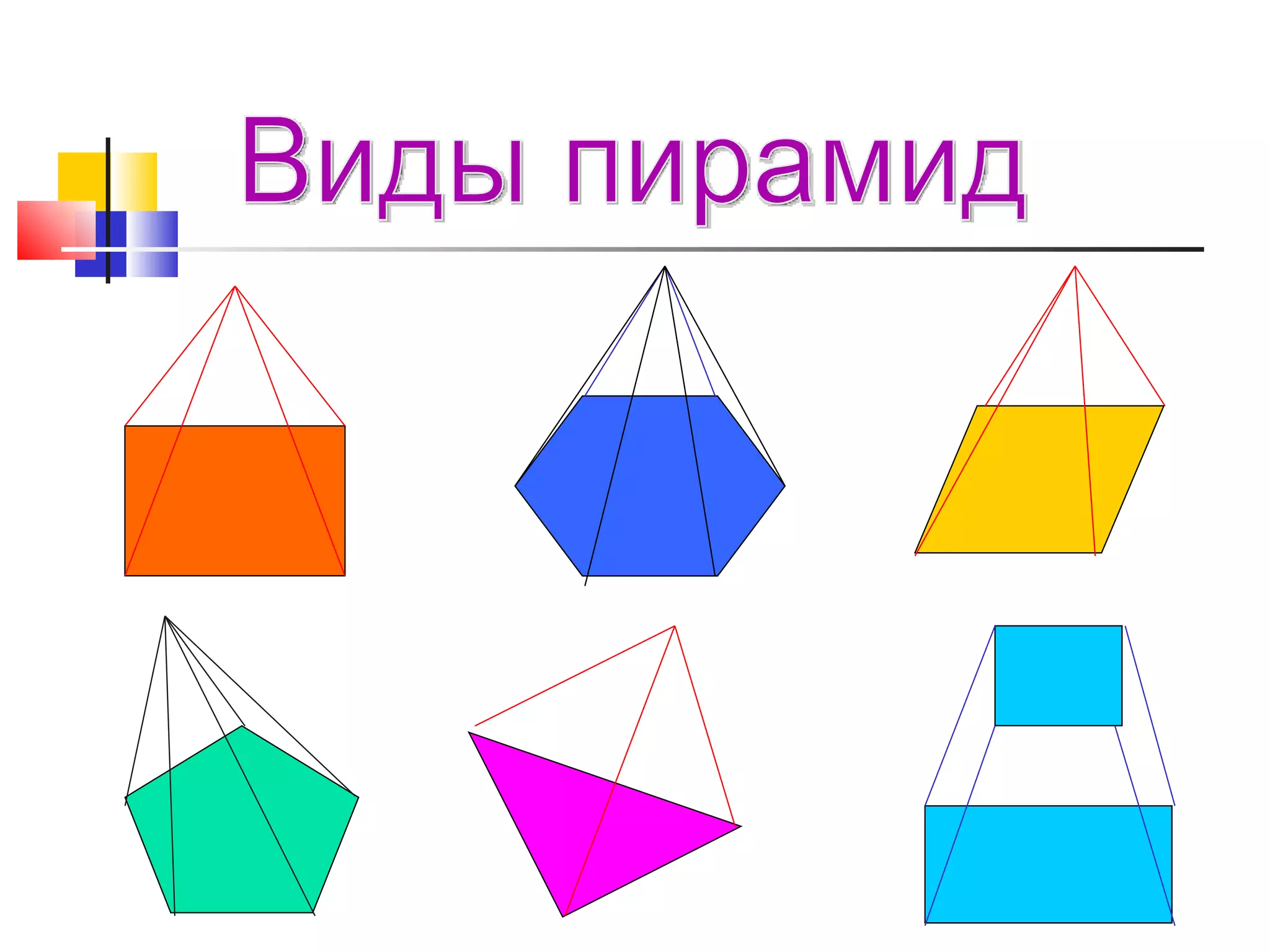
Документ описывает основные понятия и формулы, связанные с многоугольниками и пирамидами, включая вычисление площадей различных фигур и характеристики пирамид. Также рассматриваются виды пирамид, их свойства и взаимосвязи между различными элементами, такими как высоты и апофемы. В документе представлены задачи и вопросы, которые помогают закрепить материал и проверить понимание темы.

1. Повторение опорных формул Многоугольник Формулы для вычисления площади Произвольный треугольник

2. Повторение опорных формул Многоугольник Формулы для вычисления площади Равносторонний треугольник Прямоугольный треугольник Квадрат Прямоугольник Параллелограмм Ромб

3. Повторение опорных формул Многоугольник Формулы для вычисления площади Трапеция Правильный многоугольник

4. Определение: поверхность составленную из многоугольника и n треугольников, ограничивающую некоторое геометрическое тело, называется пирамидой. Понятие пирамиды

5. Многоугольники, из которых составлена пирамида, называются его гранями. Многоугольник называется основанием пирамиды, треугольники – его боковыми гранями. Понятие граней пирамиды A B C D F P

6. Стороны боковых граней называются боковыми ребрами, стороны основания называются ребрами основания , а концы ребер- вершинами многогранника Ребра и вершины пирамиды. A B C D F P

7. Отрезок, проведенный из вершины пирамиды, перпендикулярно основанию, называется высотой пирамиды . Высота пирамиды A B C D F P

8. Правильной пирамидой называется пирамида, в основании которой лежит правильный многоугольник и высота пирамиды проецируется в центр основания. Апофемой пирамиды называется высота боковой грани. H Правильная пирамида О АВС DF – правильный пятиугольник, О – центр основания, РО – высота , РН - апофема A B C D F P

9. Виды пирамид

10. Укажите многогранник, не являющийся выпуклым. Какие из данных многогранников – пирамиды. Укажите на рис. 1 и рис. 11 высоту пирамиды, апофему. Какая из пирамид может быть правильной. Укажите на рис.1 угол, который образует c плоскостью основания ребро , если - высота пирамиды. Вычислите этот угол, если проекция бокового ребра на плоскость основания в два раза меньше этого ребра. Докажите, что диагональное сечение пирамиды на рис. 11 перпендикулярно плоскости основания, если - высота призмы. Вопросы

11. Дана правильная пирамида. Отметьте на чертеже угол, который образует : а) ребром пирамиды с плоскостью основания; б) боковая грань с плоскостью основания; в) вычислить отмеченные углы. Решение по готовым чертежам

12. Сколько вершин, ребер, граней имеет шестиугольная пирамида. Какое наименьшее число граней, ребер, вершин может иметь пирамида. Как называется пирамида, у которой каждая грань может служит основанием. Сколько апофем можно провести в четырехугольной пирамиде; треугольной пирамиде. Какой отрезок служит проекцией апофемы правильной пирамиды на плоскость основания. Итоги урока: