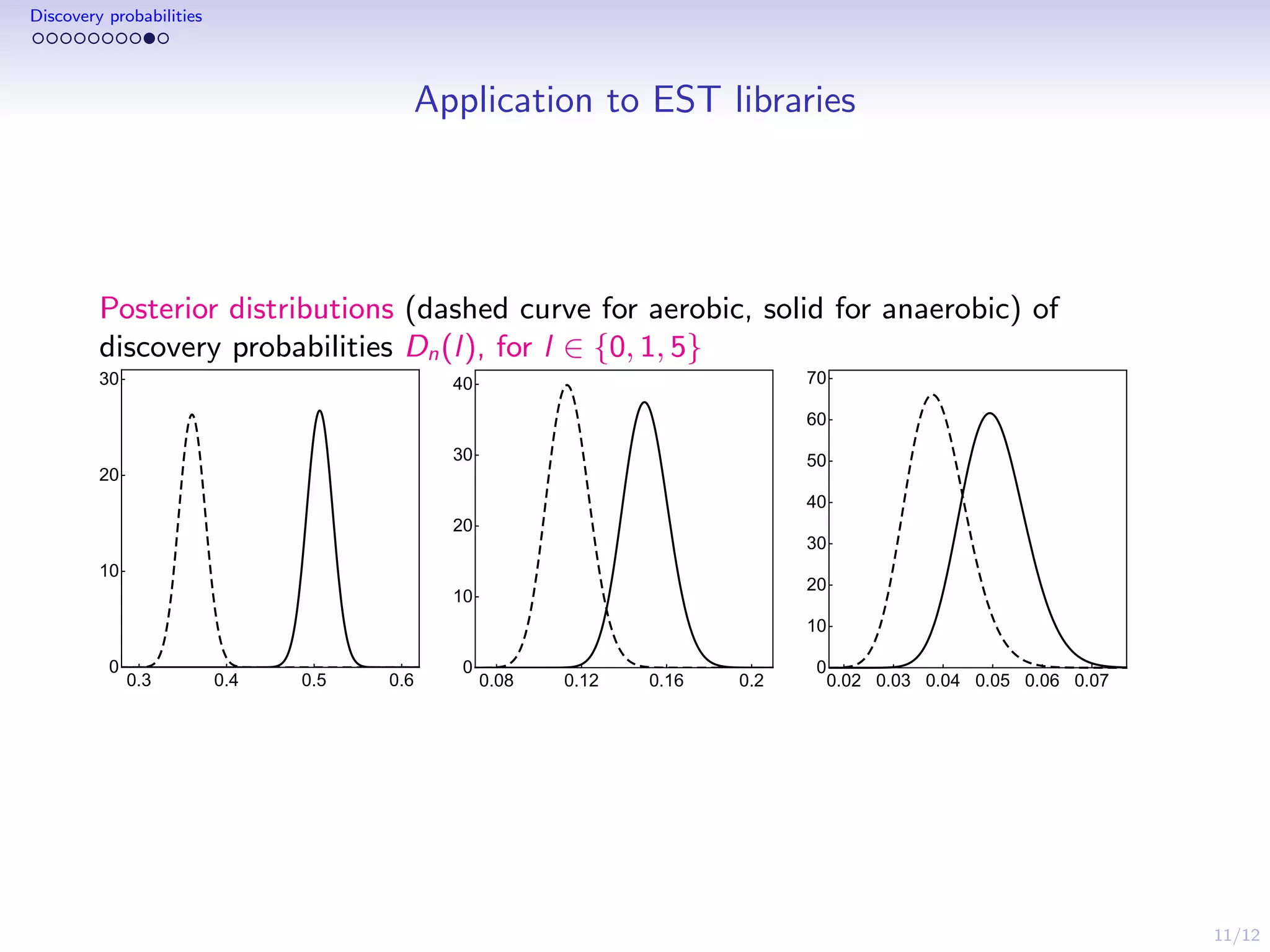
This document discusses species sampling models and discovery probabilities. It introduces the problem of estimating the probability of observing a new species given a sample. Good and Turing proposed an estimator for this during World War II. Bayesian nonparametric models provide an alternative approach by placing a prior on unknown species proportions. The document outlines BNP estimators for discovery probabilities and how credible intervals can be derived. It applies these methods to genomic datasets of expressed sequence tags to estimate discovery probabilities for observing new genes.

1. Species sampling models
julyan.arbel@carloalberto.org www.julyanarbel.com
Bocconi University, Milan, Italy & Collegio Carlo Alberto, Turin
Statalks Seminar @ Collegio Carlo Alberto
February 12, 2016
1/12

2. 2/12
Discovery probabilities
Table of Contents
Discovery probabilities

3. 3/12
Discovery probabilities
Discovery problem: motivating example
What is the probability of observing a new species?

4. 4/12
Discovery probabilities
Discovery problem: motivating example
Good and Turing worked on this problem Bletchley Park to crack German
ciphers for the Enigma machine during World War II
They proposed the estimator
Number of species observed once
Total number of species

5. 5/12
Discovery probabilities
Discovery problem
• Population of individuals (Xi )i≥1 belonging to an ideally an infinite
number of species (θi )i≥1, respective unknown proportions (pi )i≥1
• Given (X1, . . . , Xn), make inference on the probability that the (n + 1)-th
observation coincides with a species whose frequency is l, for
l = 0, 1, . . . , n. This probability is termed l-discovery, that is
Dn(l) =
i≥1
pi I{l}(˜ni )
where ˜ni is the frequency of the species of type θi in the sample
• Dn(0) denotes the proportion of yet unobserved species, or the probability
of discovering a new species, or the missing mass
• Applications arising from ecology, biology, design of experiments,
bioinformatics, genetics, linguistic, economics, network modeling,
chemistry, ...

6. 6/12
Discovery probabilities
BNP model
• The BNP approach for estimating Dn(l) is based on the randomization of
the unknown species proportions pi ’s. See Lijoi, Mena and Pr¨unster (2007)
Let P = i≥1 pi δθ denote a discrete random probability measure
Let Xn = (X1, . . . , Xn) be a sample from a population with composition P,
namely
Xi | P
iid
∼ P
P ∼ Q
with P playing the role of the nonparametric prior
• Due to the discreteness of P, the sample Xn from P exhibits ties with
positive probability. In other terms Xn features k distinct observations
X∗
1 , . . . , X∗
Kn
with corresponding frequencies (n1, . . . , nk )
• The information provided by (n1, . . . , nk ) can be coded by
mn = (m1, . . . , mn) where mi = number of species in the sample Xn
having frequency i
Under this alternative codification one obtains 1≤i≤n mi = k and
1≤i≤n imi = n.

7. 7/12
Discovery probabilities
Good Turing estimators of discovery
Remember, Good and Turing estimate the prob. of observing a new species as
Number of species observed once
Total number of species
ie
ˇDn(0) =
m1
n
Also generalized to any frequency l ≤ n
ˇDn(l) =
(l + 1)ml+1
n
Good (1953)
BNP counterparts of these estimators?

8. 8/12
Discovery probabilities
BNP estimators of discovery
Gibbs-type random probability measure P with index σ ∈ (0, 1): it is
characterized by (it induces) a predictive distribution of the form
P[Xn+1 ∈ A | Xn] =
Vn+1,kn+1
Vn,kn
G0(A) +
Vn+1,kn
Vn,kn
kn
i=1
(ni − σ) δX∗
i
(A),
BNP estimator ˆDn(l) of Dn(l) derived from the predictive using sets
A0 = X{X∗
1 , . . . , X∗
Kn
} and Al = {X∗
i : Ni,n = l}
BNP Good Turing
ˆDn(0) = E[Ph(A0) | Xn] =
Vn+1,kn+1
Vn,kn
ˇDn(l) = m1
n
ˆDn(l) = E[Ph(Al ) | Xn] = (l − σ)ml
Vn+1,kn
Vn,kn
ˇDn(l) =
(l+1)ml+1
n

9. 9/12
Discovery probabilities
Credible intervals for discovery
• Special case of Pitman–Yor process (Perman, Pitman and Yor, 1992).
For σ ∈ (0, 1) and θ > −σ and
Vn,kn =
kn−1
i=1 (θ + iσ)
(θ + 1)(n−1)
Then closed form expression for the posterior distribution as Beta
Pp(A0) | Xn
d
= Bθ+σkn,n−σkn
and
Pp(Al ) | Xn
d
= B(l−σ)ml ,θ+n−(l−σ)ml
• Similar results in the general Gibbs class
• Practical tool for deriving credible intervals for the BNP estimator ˆDn(l),
for any l = 0, 1, . . . , n. This is typically done by performing a numerical
evaluation of appropriate quantiles of the distribution of Pp(Al ) | Xn

10. 10/12
Discovery probabilities
Application to EST libraries
Application to genomic datasets called Expressed Sequence Tags (EST)
libraries
• Naegleria gruberi aerobic library consists of n = 959 ESTs with kn = 473
distinct genes and ml,959 = 346, 57, 19, 12, 9, 5, 4, 2, 4, 5, 4, 1, 1, 1, 1, 1, 1,
for l∈{1, 2, . . . , 12} ∪ {16, 17, 18} ∪ {27} ∪ {55}
• Naegleria gruberi anaerobic library consists of n = 969 ESTs with
kn = 631 distinct genes and ml,969 = 491, 72, 30, 9, 13, 5, 3, 1, 2, 0, 1, 0, 1,
for l ∈ {1, 2, . . . , 13}
• Prior specification: Pitman–Yor process, with empirical Bayes procedure
for estimating (σ, θ)
• ˆσ = 0.669, ˆθ = 46.241 for the Naegleria gruberi aerobic library
• ˆσ = 0.656, ˆθ = 155.408 for the Naegleria gruberi anaerobic library

11. 11/12
Discovery probabilities
Application to EST libraries
Posterior distributions (dashed curve for aerobic, solid for anaerobic) of
discovery probabilities Dn(l), for l ∈ {0, 1, 5}
0.3 0.4 0.5 0.6
0
10
20
30
0.08 0.12 0.16 0.2
0
10
20
30
40
0.02 0.03 0.04 0.05 0.06 0.07
0
10
20
30
40
50
60
70

12. 12/12
Discovery probabilities
Conclusion
Take-home messages
We have seen that Bayesian nonparametric methods allow for
• smoothing estimation of the discovery probabilities Dn(l) via more robust
estimators than frequentist counterparts
• a principled treatment of uncertainty where credible intervals can be
obtained naturally: closed form expression of the posterior distribution