Downloaded 37 times
Uploaded byNumenta
Sparsity In The Neocortex, And Its Implications For Machine Learning
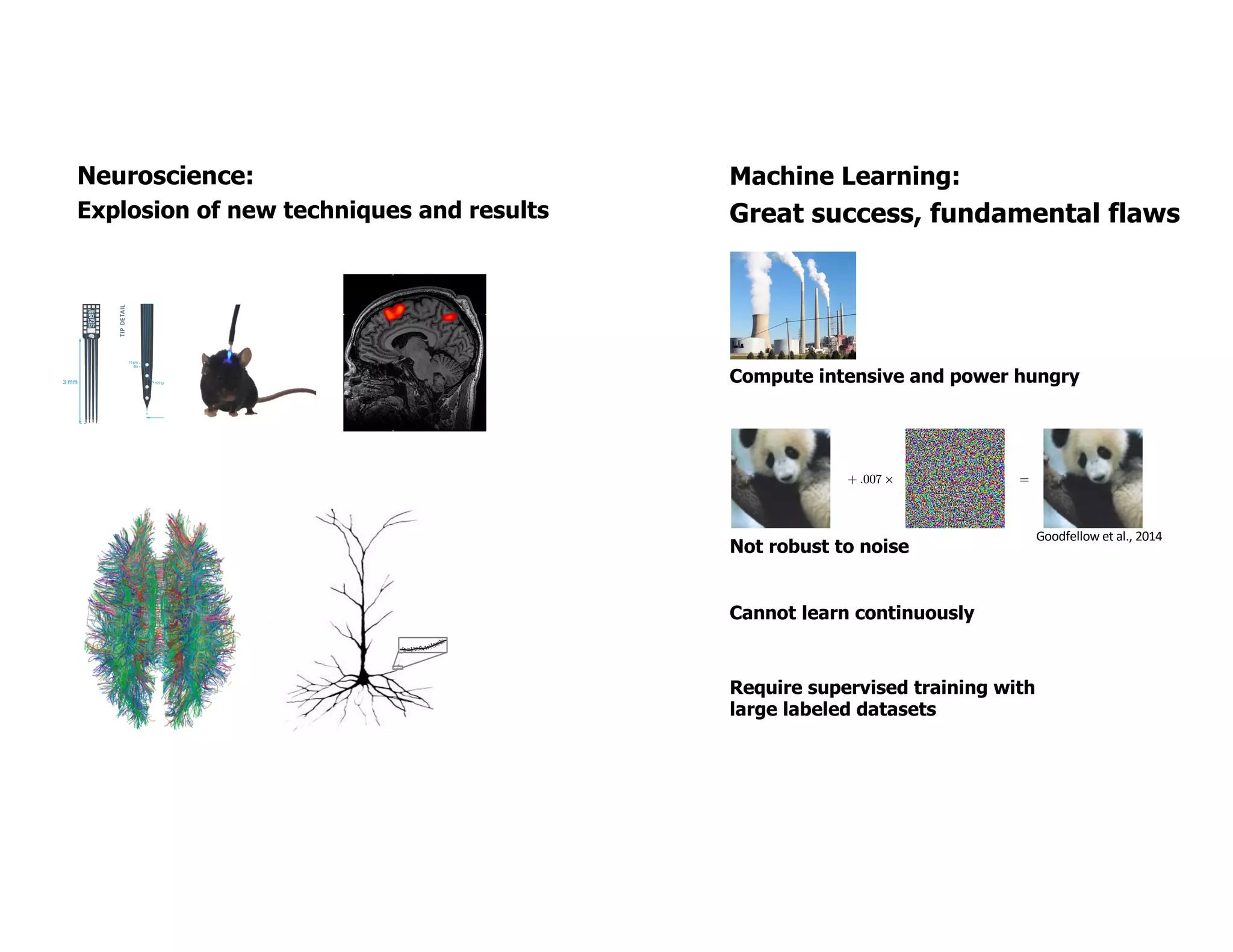
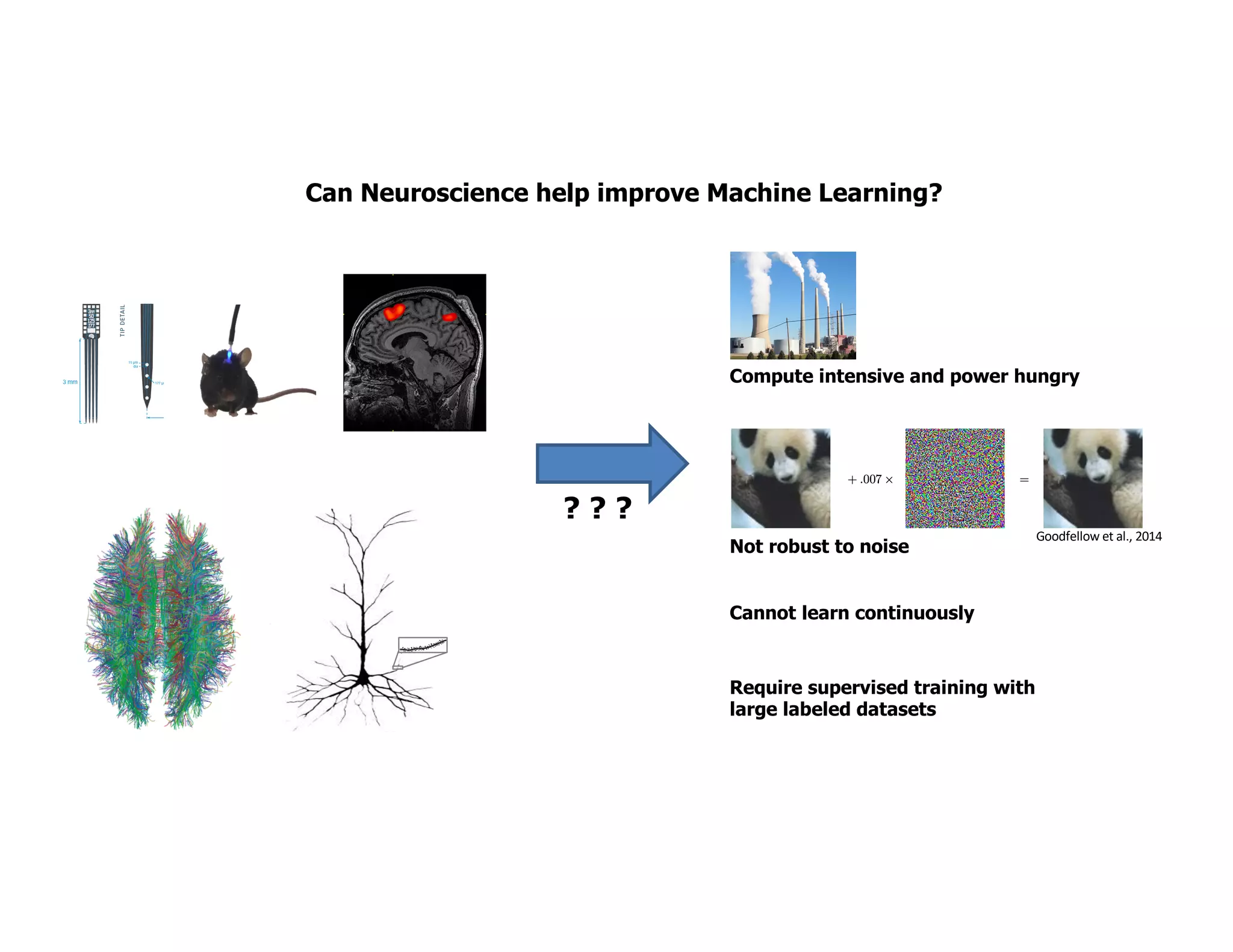
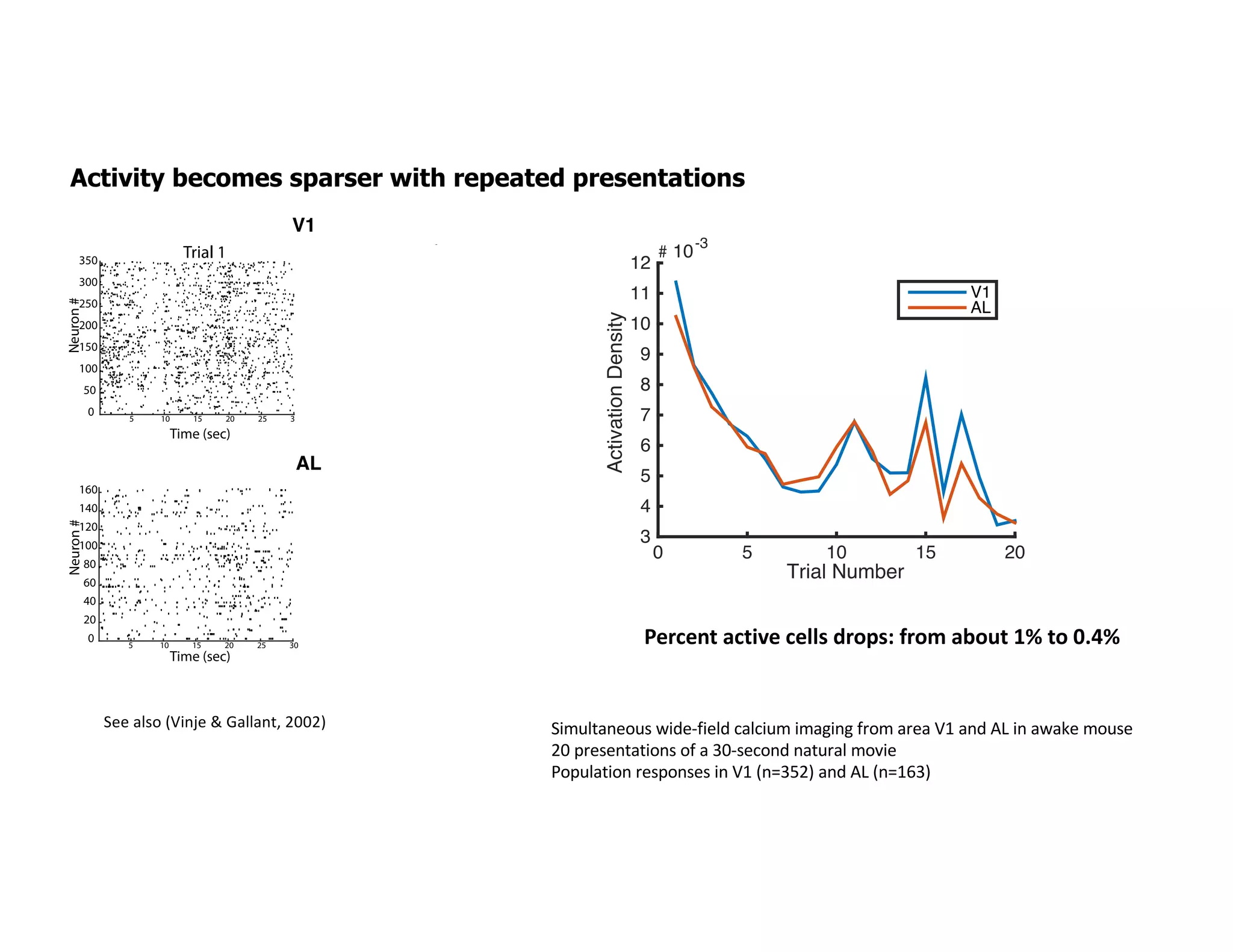
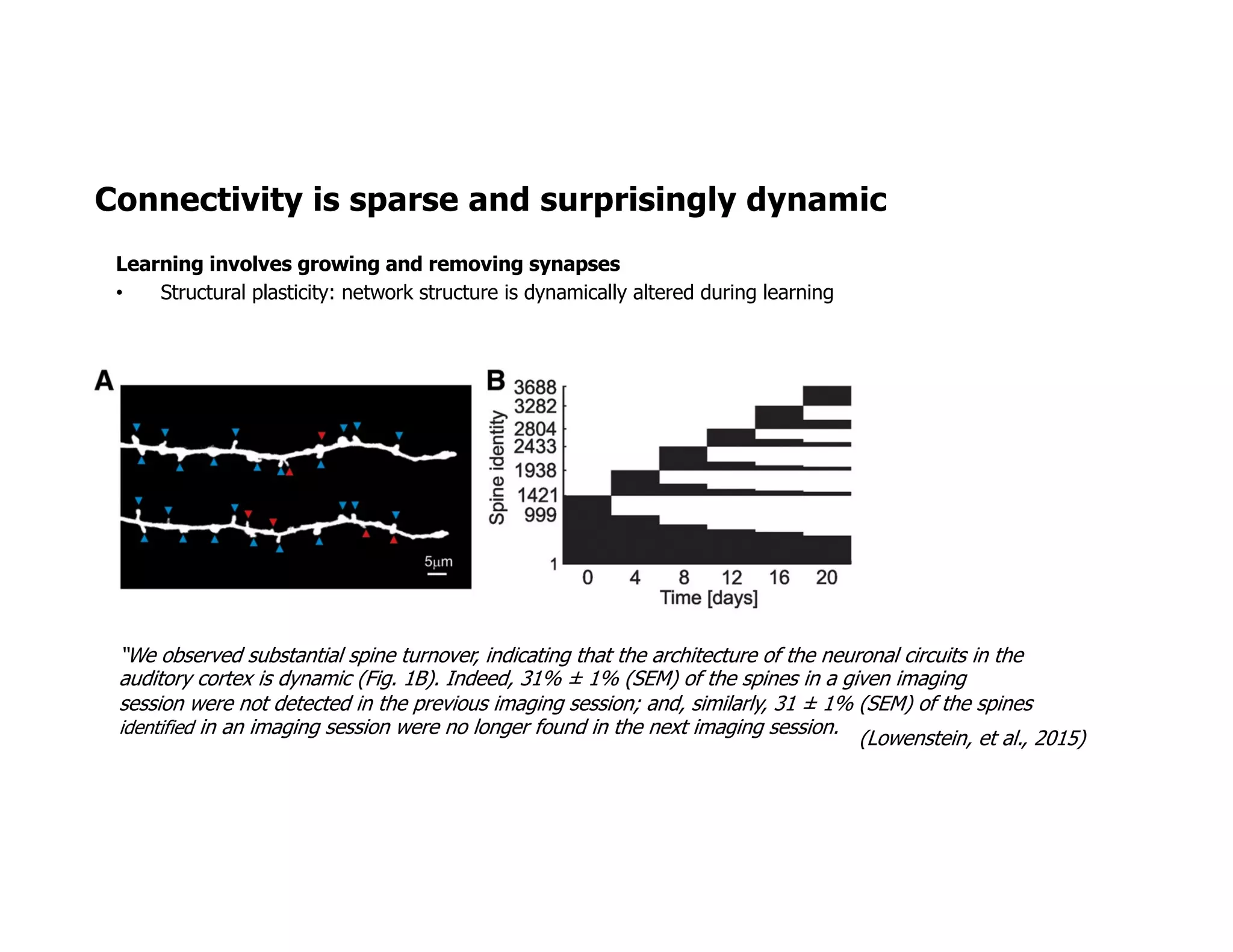
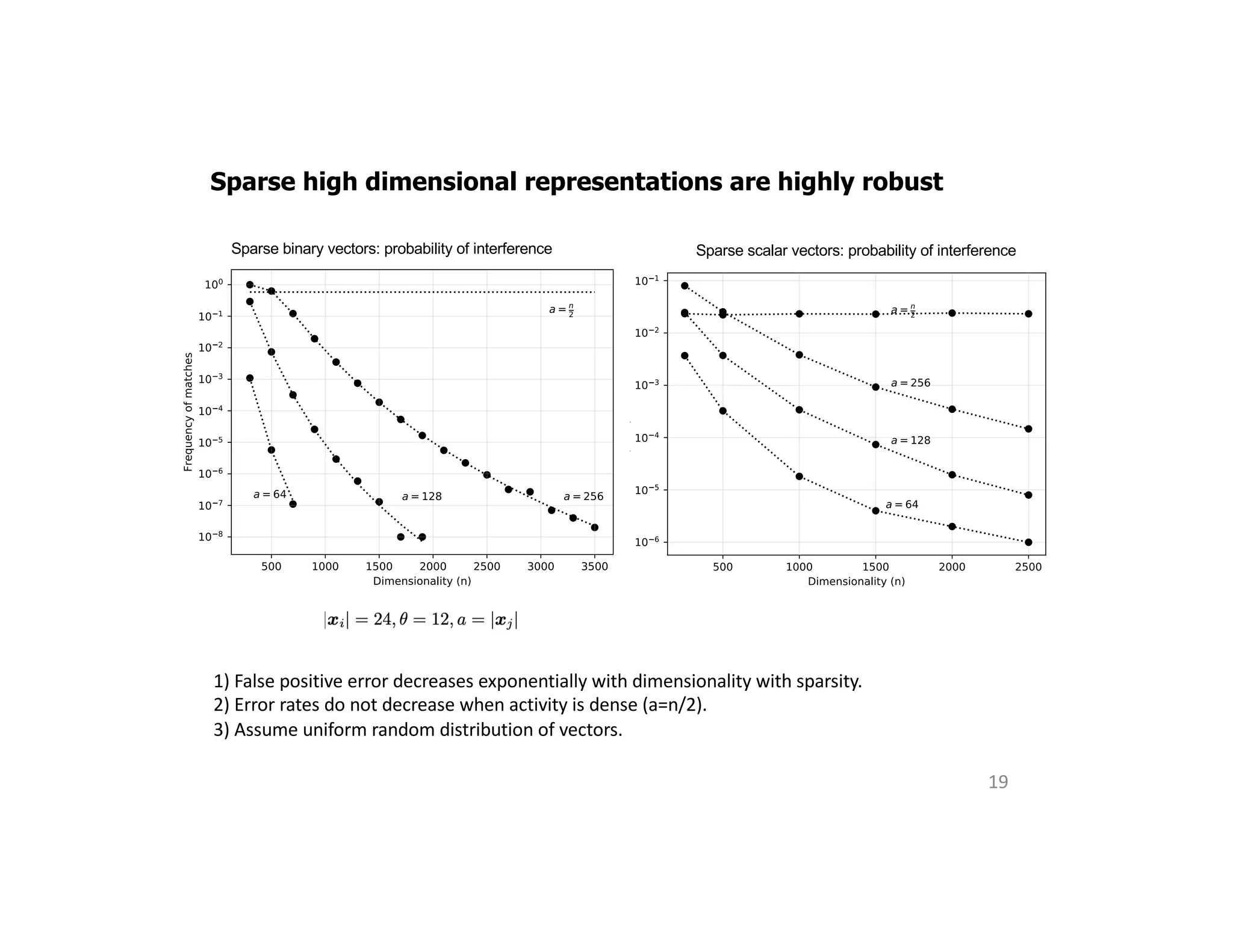
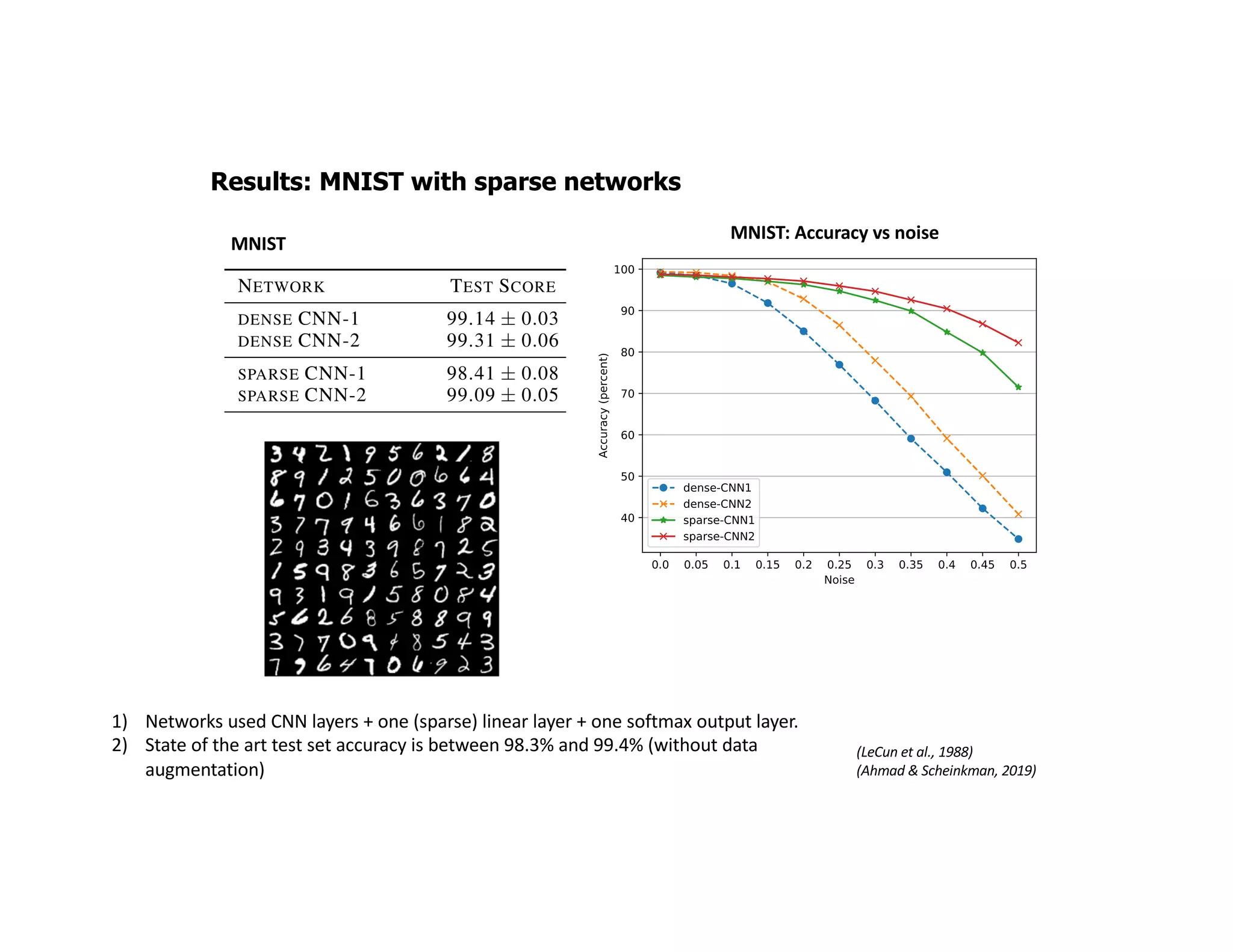
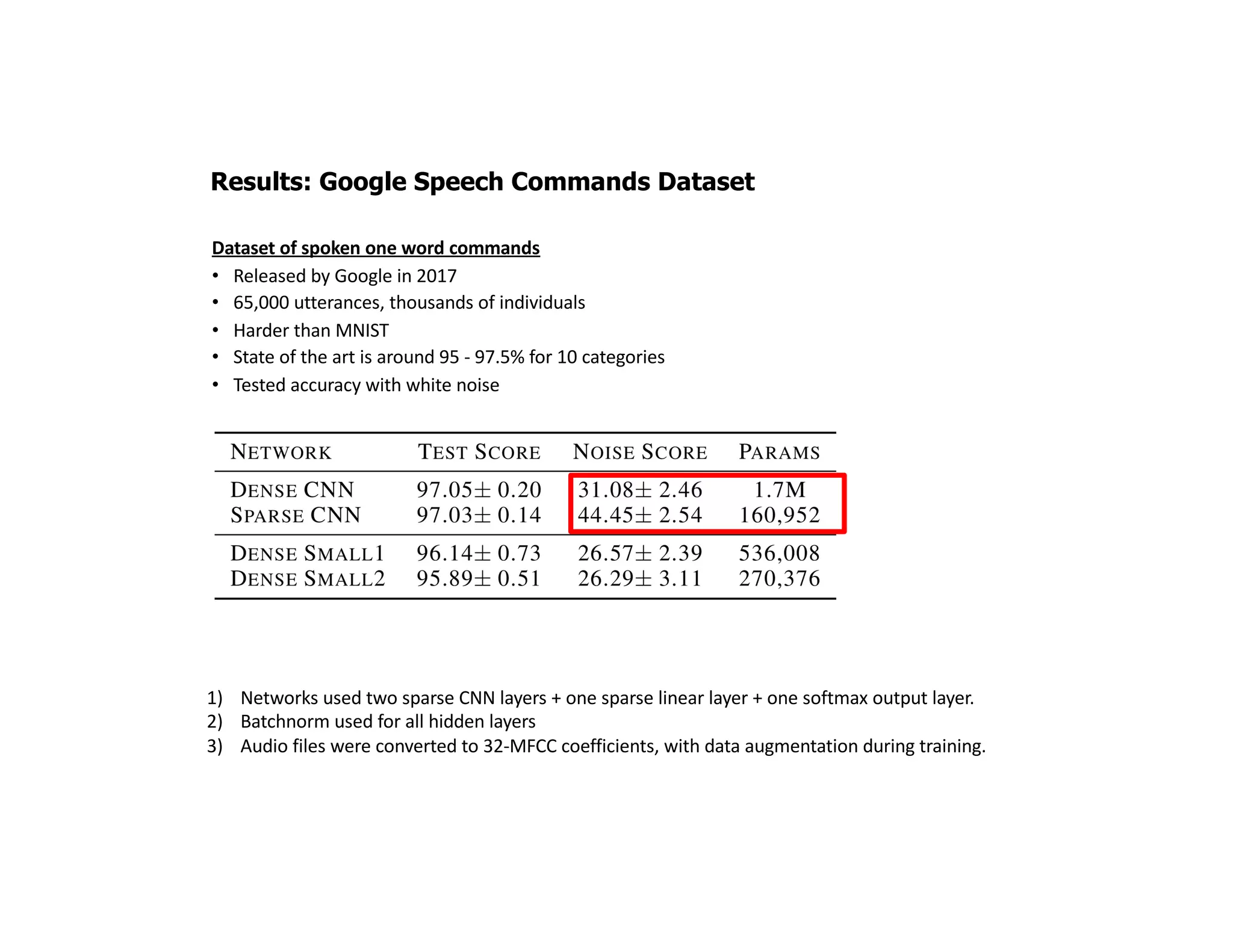
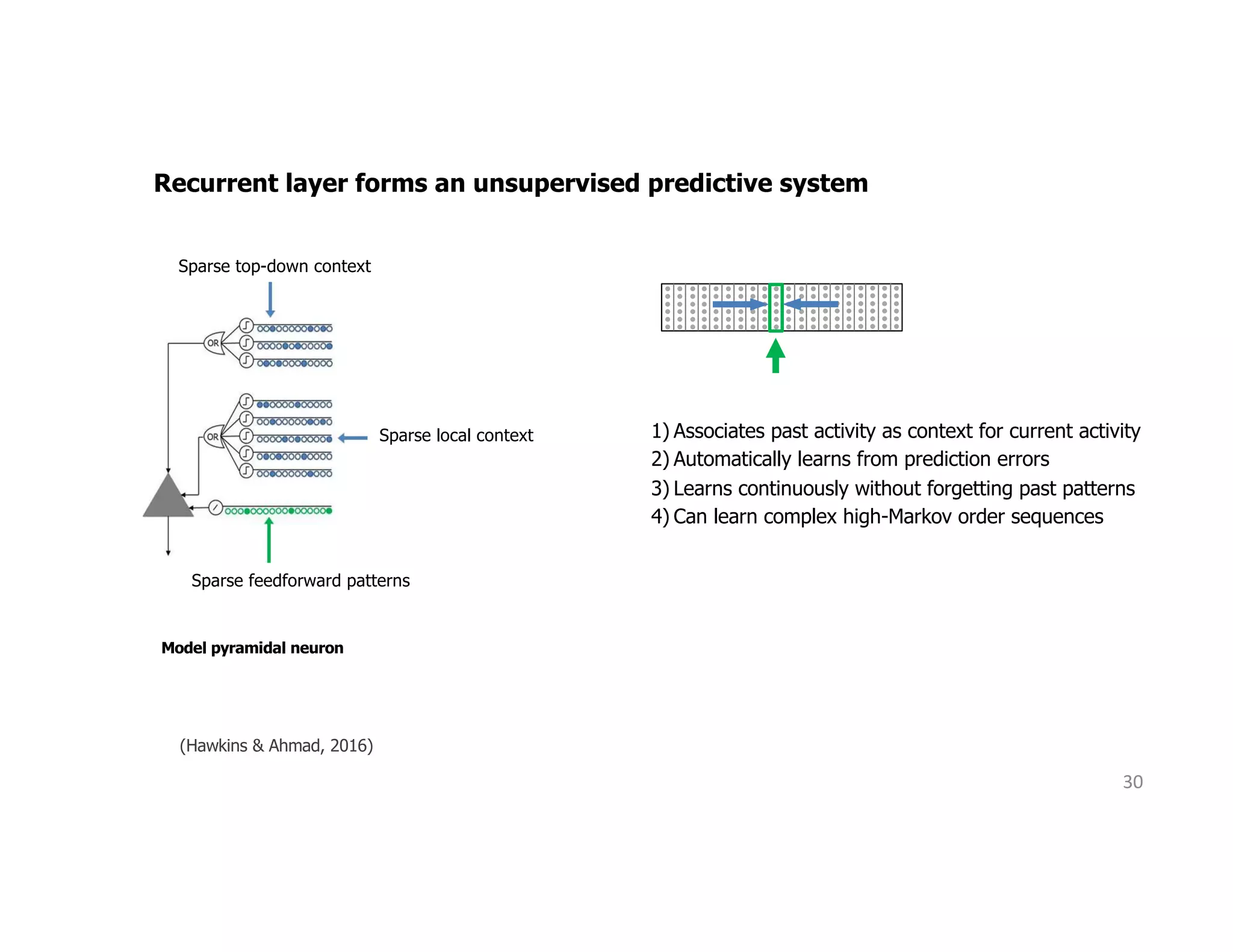
The document discusses the principles of sparsity in the neocortex and its implications for improving machine learning. It highlights three types of sparsity: population, lifetime, and connection sparsity, and emphasizes that a small percentage of neurons are active at any given time. The paper argues that understanding these principles can inform better AI techniques aimed at more efficient and robust systems.
More Related Content
Similar to Sparsity In The Neocortex, And Its Implications For Machine Learning
Sparsity In The Neocortex, And Its Implications For Machine Learning
- 1. Yale University Sparsity InThe Neocortex, And Its Implications For Machine Learning November 18, 2019 Subutai Ahmad sahmad@numenta.com @SubutaiAhmad
- 2. 1) Reverse engineerthe neocortex - biologically accurate theories - open access neuroscience publications 2) Apply neocortical principles to AI - improve current techniques - move toward truly intelligent systems Mission Founded in 2005, by Jeff Hawkins and Donna Dubinsky
- 3. Neuroscience: Explosion of newtechniques and results Machine Learning: Great success, fundamental flaws Compute intensive and power hungry Goodfellow et al., 2014 Not robust to noise Cannot learn continuously Require supervised training with large labeled datasets
- 4. Compute intensive andpower hungry Goodfellow et al., 2014 Not robust to noise Cannot learn continuously Require supervised training with large labeled datasets ? ? ? Can Neuroscience help improve Machine Learning?
- 5. Source: Prof. Hasan,Max-Planck-Institute for Research
- 6. What exactly is“sparsity”? “mostly missing” sparse vector = vector with mostly zero elements Most papers describe three types of sparsity: 1) Population sparsity How many neurons are active right now? Estimate: roughly 0.5% to 2% of cells are active at a time (Attwell & Laughlin, 2001; Lennie, 2003).
- 7. Population sparsity changeswith learning Cell Assembly Order 3 4 5 6 Numberofunique cellassemblies x104 0 1 2 3 4 5 6 7 Trial Number 0 5 10 15 20ActivationDensity # 10 -3 3 4 5 6 7 8 9 10 11 12 V1 AL Subsetindex 0 0.01 0.02 0.03 0.04 AL D ataShuffled Poisson Subsetindex 0 0.02 0.04 0.06 0.08 V1 Trial 1 Trial 20 Visual Stimulus Screen A Time (sec) 5 10 15 20 25 30 Neuron# 0 50 100 150 200 250 300 350 Time (sec) 5 10 15 20 25 30 Neuron# 0 50 100 150 200 250 300 350 Time (sec) 5 10 15 20 25 30 Neuron# 0 20 40 60 80 100 120 140 160 Time (sec) 5 10 15 20 25 30 Neuron# 0 20 40 60 80 100 120 140 160 Cell Assembly Order 3 4 5 6 0 500 1000 1500 2000 2500 3000 Data Shuffled Poisson D ataShuffled Poisson ALV1 ALV1 V1 AL B C F E D 3-order cell assembly single cell -1 -0.5 0 0.5 1 0 0.1 0.2 0.3 -1 -0.5 0 0.5 1 0 0.02 0.04 0.06 0.08 Time jitter (sec) Prob.ofobserving repeatedcellassembly Time jitter (sec) Prob.ofobserving repeatedcellassembly Spencer L. Smith (Stirman et al, 2016) YiYi Yu
- 8. Activity becomes sparserwith repeated presentations Cell Assembly Order 3 4 5 6 Numberofunique cellassemblies x104 0 1 2 3 4 5 6 7 Trial Number 0 5 10 15 20 ActivationDensity 3 4 5 6 7 8 9 10 11 V1 AL Subsetindex 0 0.01 0.02 0.03 0.04 D ataShuffled Poisson Subsetindex 0 0.02 0.04 0.06 0.08 Trial 1 Trial 20 Visual Stimulus Screen Time (sec) 5 10 15 20 25 30 Neuron# 0 50 100 150 200 250 300 350 Time (sec) 5 10 15 20 25 30 Neuron# 0 50 100 150 200 250 300 350 Time (sec) 5 10 15 20 25 30 Neuron# 0 20 40 60 80 100 120 140 160 Time (sec) 5 10 15 20 25 30 Neuron# 0 20 40 60 80 100 120 140 160 Cell Assembly Order 3 4 5 6 0 500 1000 1500 2000 2500 3000 Data Shuffled Poisson D ataShuffled Poisson ALV1 ALV1 V1 AL 3-order cell assembly single cell -1 -0.5 0 0.5 1 0 0.1 0.2 0.3 -1 -0.5 0 0.5 1 0 0.02 0.04 0.06 0.08 Time jitter (sec) Prob.ofobserving repeatedcellassembly Time jitter (sec) Prob.ofobserving repeatedcellassembly Cell Assembly Order 3 4 5 6 Numberofunique cellassemblies x104 0 1 2 3 4 5 6 7 Trial Number 0 5 10 15 20 ActivationDensity # 10-3 3 4 5 6 7 8 9 10 11 12 V1 AL D ataShuffled Poisson Subsetindex 0 0.02 0.04 0.06 0.08 V1 Trial 1 Trial 20 Visual Stimulus Screen Time (sec) 5 10 15 20 25 30 Neuron# 0 50 100 150 200 250 300 350 Time (sec) 5 10 15 20 25 30 0 50 100 150 200 250 300 350 140 160 140 160 Cel 3 0 500 1000 1500 2000 2500 3000V1 AV1 V1 AL 0.3 0.08 ly bly See also (Vinje & Gallant, 2002) Simultaneous wide-field calcium imaging from area V1 and AL in awake mouse 20 presentations of a 30-second natural movie Population responses in V1 (n=352) and AL (n=163) Percent active cells drops: from about 1% to 0.4%
- 9. What exactly is“sparsity”? “mostly missing” sparse vector = vector with mostly zero elements Most papers describe three types of sparsity: 1) Population sparsity How many neurons are active right now? Estimate: roughly 0.5% to 2% of cells are active at a time (Attwell & Laughlin, 2001; Lennie, 2003). 2) Lifetime sparsity How often does a given cell fire? 3) Connection sparsity If a group or layer of cells projects to another layer, what percentage are physically connected? Estimate: 1% - 5% of possible neuron to neuron connections exist (Holmgren et al., 2003).
- 10. Connectivity is sparseand surprisingly dynamic “We observed substantial spine turnover, indicating that the architecture of the neuronal circuits in the auditory cortex is dynamic (Fig. 1B). Indeed, 31% ± 1% (SEM) of the spines in a given imaging session were not detected in the previous imaging session; and, similarly, 31 ± 1% (SEM) of the spines identified in an imaging session were no longer found in the next imaging session. (Lowenstein, et al., 2015) Learning involves growing and removing synapses • Structural plasticity: network structure is dynamically altered during learning
- 11. What exactly is“sparsity”? “mostly missing” sparse vector = vector with mostly zero elements Most papers describe three types of sparsity: 1) Population sparsity How many neurons are active right now? Estimate: roughly 0.5% to 2% of cells are active at a time (Attwell & Laughlin, 2001; Lennie, 2003). 2) Lifetime sparsity How often does a given cell fire? 3) Connection sparsity If a group or layer of cells projects to another layer, what percentage are physically connected? Estimate: 1% - 5% of possible neuron to neuron connections exist (Holmgren et al., 2003). …but there’s more to sparsity…
- 12. Source: Smirnakis Lab,Baylor College of Medicine
- 13. Dendrites of corticalneurons detect sparse patterns (Mel, 1992; Branco & Häusser, 2011; Schiller et al, 2000; Losonczy, 2006; Antic et al, 2010; Major et al, 2013; Spruston, 2008; Milojkovic et al, 2005, etc.) Major, Larkum and Schiller 2013 13 Pyramidal neuron 3K to 10K synapses Dendrites contain dozens of independent computational segments These segments become active with cluster of 10-20 active synapses Neurons detect highly sparse patterns, in parallel
- 14. Pyramidal neuron Sparse feedforwardpatterns Sparse local patterns Sparse top-down patterns 14 Learning localized to dendritic segments “Branch specific plasticity” If cell becomes active: • If there was a dendritic spike, reinforce that segment • If there were no dendritic spikes, grow connections by subsampling cells active in the past If cell is not active: • If there was a dendritic spike, weaken the segments Sparse learning: only a small part of the neuron is updated (Gordon et al., 2006; Losonczy et al., 2008; Yang et al., 2014; Cichon & Gang, 2015; El- Boustani et al., 2018; Weber et al., 2016; Sander et al., 2016; Holthoff et al., 2004)
- 15. Sparsity is deeplyingrained in the neocortex 1) Dynamic population sparsity A small percent of neurons are active at any time 2) Lifetime sparsity Cells don’t fire very often 3) Sparse dynamic connections Connected to a small percent of potential connections 4) Neurons detect sparse patterns Dozens of independent segments detect sparse patterns 5) Sparse learning Tiny percentage of synapses are updated during learning 6) Sparse synapse weights Highly quantized, close to binary 7) Sparse energy usage
- 17. On a singleneuron, 8-20 synapses on tiny segments of dendrites can recognize patterns. Thousands of other neurons send input to it. How can neurons recognize patterns robustly using a tiny fraction of available connections and highly sparse activations? Mathematics of highly sparse representations Pyramidal neuron 3K to 10K synapses xi<latexit sha1_base64="(null)">(null)</latexit><latexit sha1_base64="(null)">(null)</latexit><latexit sha1_base64="(null)">(null)</latexit><latexit sha1_base64="(null)">(null)</latexit> n inputs<latexit sha1_base64="dwl2mcnPQNgv8dEIjD6vL0j60R0=">AAAB+XicbVDLSsNAFJ3UV62vqEtFBovgqiS60GXRjcsW7APaUCbTSTt0MgkzN8USuvQv3LhQxK2bfoc7v8GfcJp2oa0HLhzOuZd77/FjwTU4zpeVW1ldW9/Ibxa2tnd29+z9g7qOEkVZjUYiUk2faCa4ZDXgIFgzVoyEvmANf3A79RtDpjSP5D2MYuaFpCd5wCkBI3VsW+I2sAdIMZdxAnrcsYtOycmAl4k7J8Xy8aT6/XgyqXTsz3Y3oknIJFBBtG65TgxeShRwKti40E40iwkdkB5rGSpJyLSXZpeP8ZlRujiIlCkJOFN/T6Qk1HoU+qYzJNDXi95U/M9rJRBce2n2E5N0tihIBIYIT2PAXa4YBTEyhFDFza2Y9okiFExYBROCu/jyMqlflNzLklM1adygGfLoCJ2ic+SiK1RGd6iCaoiiIXpCL+jVSq1n6816n7XmrPnMIfoD6+MHppeXXg==</latexit> P(xi · xj ✓)<latexit sha1_base64="(null)">(null)</latexit><latexit sha1_base64="(null)">(null)</latexit><latexit sha1_base64="(null)">(null)</latexit><latexit sha1_base64="(null)">(null)</latexit><latexit sha1_base64="(null)">(null)</latexit><latexit sha1_base64="(null)">(null)</latexit><latexit sha1_base64="(null)">(null)</latexit><latexit sha1_base64="(null)">(null)</latexit><latexit sha1_base64="(null)">(null)</latexit><latexit sha1_base64="(null)">(null)</latexit><latexit sha1_base64="(null)">(null)</latexit><latexit sha1_base64="(null)">(null)</latexit><latexit sha1_base64="(null)">(null)</latexit> Binary sparse vector matching = connections on dendrite = input activity
- 18. We can getexcellent stability and robustness by reducing , at the cost of increased “false positives” and interference. Can compute the probability of a random vector matching a given : Numerator: volume around point (white) Denominator: full volume of space (grey) P (xi · xj ✓) = P|xi| b=✓ | ⌦n (xi, b, |xj|) | n |xj |<latexit sha1_base64="(null)">(null)</latexit><latexit sha1_base64="(null)">(null)</latexit><latexit sha1_base64="(null)">(null)</latexit><latexit sha1_base64="(null)">(null)</latexit> |⌦n (xi, b, k)| = ✓ |xi| b ◆✓ n |xi| k b ◆ <latexit sha1_base64="(null)">(null)</latexit><latexit sha1_base64="(null)">(null)</latexit><latexit sha1_base64="(null)">(null)</latexit><latexit sha1_base64="(null)">(null)</latexit> xi<latexit sha1_base64="(null)">(null)</latexit><latexit sha1_base64="(null)">(null)</latexit><latexit sha1_base64="(null)">(null)</latexit><latexit sha1_base64="(null)">(null)</latexit> P(xi · xj ✓)<latexit sha1_base64="(null)">(null)</latexit><latexit sha1_base64="(null)">(null)</latexit><latexit sha1_base64="(null)">(null)</latexit><latexit sha1_base64="(null)">(null)</latexit><latexit sha1_base64="(null)">(null)</latexit><latexit sha1_base64="(null)">(null)</latexit><latexit sha1_base64="(null)">(null)</latexit><latexit sha1_base64="(null)">(null)</latexit><latexit sha1_base64="(null)">(null)</latexit><latexit sha1_base64="(null)">(null)</latexit><latexit sha1_base64="(null)">(null)</latexit><latexit sha1_base64="(null)">(null)</latexit><latexit sha1_base64="(null)">(null)</latexit> Sparse high dimensional representations are highly robust
- 19. Sparse high dimensionalrepresentations are highly robust 19 1) False positive error decreases exponentially with dimensionality with sparsity. 2) Error rates do not decrease when activity is dense (a=n/2). 3) Assume uniform random distribution of vectors. Sparse binary vectors: probability of interference Sparse scalar vectors: probability of interference
- 20.
- 21. A simple differentiablesparse layer (Hawkins, Ahmad, & Dubinsky, 2011) (Makhzani & Frey, 2015) (Ahmad & Scheinkman, 2019) Outputs of top-k units are maintained, the rest are set to 0. Just like ReLU, but with dynamic threshold. Weight matrix is sparse (most weights are zero). 1) An exponential boosting term favors units with low activation frequency: This helps maximize the overall entropy of the layer. 2) Easy extension to sparse convolutional layer
- 22. Results: MNIST withsparse networks 1) Networks used CNN layers + one (sparse) linear layer + one softmax output layer. 2) State of the art test set accuracy is between 98.3% and 99.4% (without data augmentation) MNIST MNIST: Accuracy vs noise (LeCun et al., 1988) (Ahmad & Scheinkman, 2019)
- 23. Sparse networks aresignificantly better on noisy data
- 24. Sparse networks aresignificantly better on noisy data
- 25. Sparse networks aresignificantly better on noisy data
- 26. Results: CIFAR-10 DenseNet • DenseNet(Huang et al., 2016), implements dense level skipping in blocks. • NotSoDenseNet: sparse transition layers and sparse linear classification layer. VGG • VGG19 as in (Simonyan & Zisserman, 2014), with batch norm • Sparse CNN layers with sparse weights, no linear layer
- 27. Results: Google SpeechCommands Dataset Dataset of spoken one word commands • Released by Google in 2017 • 65,000 utterances, thousands of individuals • Harder than MNIST • State of the art is around 95 - 97.5% for 10 categories • Tested accuracy with white noise 1) Networks used two sparse CNN layers + one sparse linear layer + one softmax output layer. 2) Batchnorm used for all hidden layers 3) Audio files were converted to 32-MFCC coefficients, with data augmentation during training.
- 28. 28 Continuous learning withactive dendrites Pyramidal neuron Sparse feedforward patterns Sparse top-down patterns Sparse local patterns
- 29. 29 (Hawkins & Ahmad,2016) Continuous learning with active dendrites Model pyramidal neuron Simple localized learning rules When a cell becomes active: 1) If a segment detected pattern, reinforce that segment 2) If no segment detected a pattern, grow new connections on new dendritic segment If cell did not become active: 1) If a segment detected pattern, weaken that segment - Learning consists of growing new connections - Neurons learn continuously but since patterns are sparse, new patterns don’t interfere with old ones Sparse top-down context Sparse local context Sparse feedforward patterns
- 30. 30 (Hawkins & Ahmad,2016) Recurrent layer forms an unsupervised predictive system Model pyramidal neuron Sparse top-down context Sparse local context Sparse feedforward patterns 1) Associates past activity as context for current activity 2) Automatically learns from prediction errors 3) Learns continuously without forgetting past patterns 4) Can learn complex high-Markov order sequences
- 31. Recurrent Neural network (ESN, LSTM) HTM* 31 Continuouslearning with streaming data sources (Cui et al, Neural Computation, Nov 2016) HTM = Hierarchical Temporal Memory 2015-04-20 Monday 2015-04-21 Tuesday 2015-04-22 Wednesday 2015-04-23 Thursday 2015-04-24 Friday 2015-04-25 Saturday 2015-04-26 Sunday 0 k 5 k 10 k 15 k 20 k 25 k 30 k PassengerCountin30minwindow A B C Shift ARIM ALSTM 1000LSTM 3000LSTM 6000 TM 0.0 0.2 0.4 0.6 0.8 1.0 NRMSE 0.00 0.05 0.10 0.15 0.20 0.25 0.30 0.35 MAPE 0.0 0.5 1.0 1.5 2.0 2.5 NegativeLog-likelihood Shift ARIM ALSTM 1000LSTM 3000LSTM 6000 TM LSTM 1000LSTM 3000LSTM 6000 TM D NYC Taxi demand datastream Source: http://www.nyc.gov/html/tlc/html/about/trip_record_data.shtml ?
- 32. Apr01 15 Apr08 15 Apr15 15 Apr22 15 Apr29 15 M ay 06 15 LSTM6000 HTMMeanabsolutepercenterror 0.06 0.08 0.10 0.12 0.14 Dynamics of patternchanged 32(Cui et al, Neural Computation, 2016) Adapts quickly to changing statistics
- 33. • Sparse connections CNN Implicationsof sparsity for machine learning
- 34. • Sparse connections •Sparse activations Improved robustness no loss of accuracy Large performance gains on hardware energy – speed – size • Compartmental neurons (aka active dendrites) Continuous learning quickly reacts to changes • Intralaminar circuits Unsupervised learning predictive learning without teacher signal CNN Point neuron Neuroscience principles inform each of these steps Need to design hardware architectures that exploit these properties Implications of sparsity for machine learning
- 36. • Sparse connections •Sparse activations Improved robustness • Compartmental neurons (aka active dendrites) Continuous learning • Intralaminar circuits Unsupervised learning • Multilaminar circuits - Reference frames - Sensory-motor 3D Object models Intelligent Robotics Point neuron From sparsity to general intelligence
- 37. Implications for hardwarearchitectures 1) Population sparsity 2) Lifetime sparsity 3) Sparse dynamic connections 4) Neurons detect sparse patterns 5) Sparse learning 6) Highly quantized synapse weights 7) Sparse energy usage