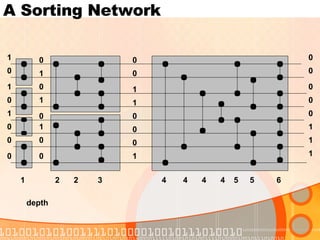
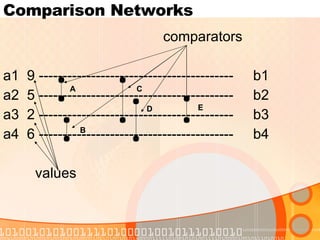
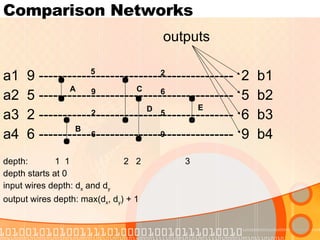
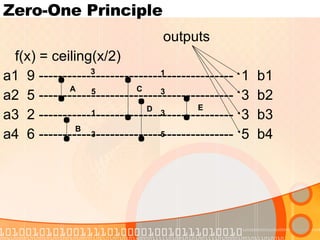
The document discusses sorting networks and their components. It describes comparison networks that use comparators to sort input sequences. A zero-one principle is presented, stating that if a network sorts all binary sequences correctly, it will sort all number sequences correctly. Bitonic sorting networks are introduced that can sort bitonic sequences using half-cleaner stages. A merging network is described that can merge two sorted sequences using a modification of the first half-cleaner stage of a bitonic sorter. Finally, a sorting network is proposed that uses merging networks in a merge sort approach to sort any input sequence in parallel.

1. SORTING NETWORKS Presented by: Vikram S. Choudhary, JECRC, Jodhpur.

2. Overview Sorting Network Components Comparison Networks Comparator Zero-one Principle Bitonic Sorting Network Half-Cleaner Bitonic Sorter Merging Network Sorting Network

3. Comparison Networks Sorting networks are Comparison Networks that always sort their inputs Comparison Network composed of: wires comparators Wires: transmits values from place to place Comparators: two inputs  two outputs

4. Comparison Networks Comparators: inputs: x and y outputs: x’ and y’ x’ = min(x, y) y’ = max(x, y) input output x   x’ = min(x, y) y   y’ = max(x, y) x ------------------------------ x’ = min(x, y) y ------------------------------ y’ = max(x, y) comparator

5. Comparison Networks Comparators n input wires: a 1 , a 2 , …, a n input sequence: < a 1 , a 2 , …, a n > n output wires: b 1 , b 2 , …, b n output sequence: <b 1 , b 2 , …, b n > Properties: requirement: graph is acyclic output produced only when input is available comparators process in parallel if input is available

6. Comparison Networks comparators a1 9 ----------------------------------------- b1 a2 5 ----------------------------------------- b2 a3 2 ----------------------------------------- b3 a4 6 ----------------------------------------- b4 values A B C D E

7. Comparison Networks outputs a1 9 ----------------------------------------- 2 b1 a2 5 ----------------------------------------- 5 b2 a3 2 ----------------------------------------- 6 b3 a4 6 ----------------------------------------- 9 b4 depth: 1 1 2 2 3 depth starts at 0 input wires depth: d x and d y output wires depth: max(d x , d y ) + 1 A B C D E 5 9 2 6 2 6 5 9

8. Comparison Networks Sorting Network is a Comparison Network where the output is sorted output sequence is monotonically increasing (b 1 <= b 2 …<= b n ) for every input sequence Not all Comparison Networks are Sorting Networks Comparison Network is like a procedure in that it specifies how comparisons are to occur

9. Zero-One Principle If a Sorting Network works correctly when each input is drawn from the set {0, 1}, then it works correctly on arbitrary input numbers (integers, reals, or values from any linearly sorted set)

10. Zero-One Principle Lemma 27.1 If a Comparison Network transforms the input sequence a = <a 1 , a 2 , …, a n > into the output sequence b = <b 1 , b 2 , …, b n >, then for any monotonically increasing function f, the network transforms the input sequence: f(a) = <f(a 1 ), f(a 2 ), …, f(a n )> into the output sequence: f(b) = <f(b 1 ), f(b 2 ), …, f(b n )>

11. Zero-One Principle Proof: prove claim: if f is a monotonically increasing function, then a single comparator with inputs f(x) and f(y) produces output f(min(x, y)) and f(max(x, y)) f(x) ------------------------------ min(f(x), f(y)) f(y) ------------------------------ max(f(x), f(y)) min(f(x), f(y)) = f(min(x, y)) max(f(x), f(y)) = f(max(x, y))

12. Zero-One Principle outputs f(x) = ceiling(x/2) a1 9 ----------------------------------------- 1 b1 a2 5 ----------------------------------------- 3 b2 a3 2 ----------------------------------------- 3 b3 a4 6 ----------------------------------------- 5 b4 A B C D E 3 5 1 3 1 3 3 5

13. Zero-One Principle Theorem 27.2 (Zero-One Principle) If a Comparison Network with n inputs sorts all 2 n possible sequences of 0’s and 1’s correctly, then it sorts all sequences of arbitrary numbers correctly.

14. Zero-One Principle Proof: By contradiction: Suppose that the network sorts all zero-one sequences, but there exists a sequence of arbitrary numbers that the network does not sort: <a 1 , a 2 , …, a n > contains elements a i and a j where a i < a j but the network places a j before a i in the output sequence

15. Zero-One Principle Define monotonically increasing function f: f(x) = { 0 if x <= a i , 1 if x > a i . a j is placed before a i in the output sequence f(a j ) placed before f(a i ) when input is <a 1 , a 2 , …, a n > since f(a j ) = 1 and f(a i ) = 0, from above we have a contradiction

16. Bitonic Sorting Network Bitonic Sequence: a sequence that monotonically increases and then decreases, or can be circularly shifted to become monotonically increasing and then monotonically decreasing examples: <1, 4, 6, 8, 3, 2>, < 6, 9, 4, 2, 3, 5>, and <9, 8, 3, 2, 4, 6> zero-one: 0 i 1 j 0 k or 1 i 0 j 1 k when i,j,k >= 0

17. Bitonic Sorting Network Half-Cleaner a bitonic sorter is composed of several stages, each of which is called a half-cleaner half-cleaner is a Comparison Network of depth 1 line i compared with i + n/2 for i = 1, 2,…, n/2 assume that n is even

18. Bitonic Sorting Network Example: Half-Cleaner[8] all 1’s or 0’s 0 ---------------------------------- 0 0 ---------------------------------- 0 bitonic 1 ---------------------------------- 0 clean bitonic 1 ---------------------------------- 0 ________ 1 ---------------------------------- 1 0 ---------------------------------- 0 bitonic 0 ---------------------------------- 1 0 ---------------------------------- 1

19. Bitonic Sorting Network Lemma 27.3 If the input to a half-cleaner is a bitonic sequence of 0’s and 1’s, then the output satisfies the following properties: both the top half and the bottom half are bitonic every element in the top half is at least as small as every element in the bottom half at least one half is clean (either all 0’s or 1’s)

20. Bitonic Sorting Network Proof: the Comparison Network Half-Cleaner[n] compares inputs i and i + n/2 for i = 1, 2, … n/2 suppose input is of the form: 00…011…100…0 there are 3 possible cases for the n/2 midpoint to fall and the situation where the midpoint falls in a block of 1’s is separated into 2 cases So 4 cases in total

21. Bitonic Sorting Network Cases: bitonic n/2 bitonic n/2 0 1 0 0 1 0 0 0 0 1 0 0 1 0 0 1 0 0 1 0 0 1 0 0 0 0 1 0 top top top top bottom bottom bottom bottom bitonic clean bitonic clean bitonic bitonic

22. Bitonic Sorting Network Cases: bitonic n/2 bitonic n/2 0 0 0 1 0 0 1 0 1 0 0 0 0 1 0 1 1 0 0 0 1 0 top top top top bottom bottom bottom bottom bitonic clean bitonic clean bitonic bitonic 0 1 1 1 1 1 1 1

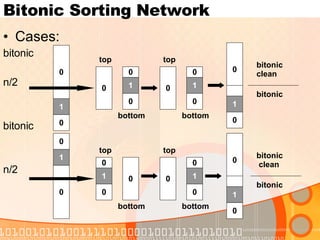
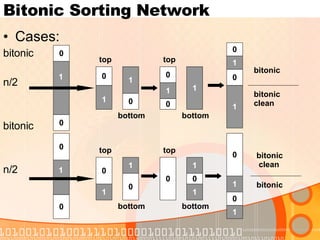
23. Bitonic Sorting Network Bitonic Sorter by recursively combining half-cleaners, we can build a bitonic sorter, a network that sorts bitonic sequences first stage: Half-Cleaner[n] subsequent sorts with Bitonic-Sorter[n/2] Depth D(n) of Bitonic-Sorter[n]: D(n) = { 0 if n =1, D(n/2) + 1 if n = 2 k and k>= 1

24. Bitonic Sorting Network Example: Half-Cleaner[n] Bitonic- Sorter[n/2] Bitonic- Sorter[n/2]

25. Bitonic Sorting Network Example: 0 0 1 1 1 0 0 0 0 0 0 0 1 0 1 1 0 0 0 0 1 0 1 1 0 0 0 0 0 1 1 1 bitonic sorted

26. Bitonic Sorting Network Bitonic-Sorter can be used to sort a zero-one sequence By the Zero-One principle it follows that any bitonic sequence of arbitrary numbers can be sorted using this network

27. A Merging Network Networks that can merge two sorted input sequences into one sorted output sequence The merging network is based on the following Given two sorted sequences, if we reverse the second sequence and then concatenate the two, the resulting sequence is bitonic. ie. given : X = 00001111 and Y = 000011111 Y R = 111110000 X● Y R = 00001111111110000

28. A Merging Network We can construct M ERGER [n] by modifying the first half cleaner of B ITONIC -S ORTER [n]. The key is to perform the reversal of the second half of the inputs implicitly. Given two sorted sequences <a 1 , a 2 , …, a n/2 > and <a n/2+1 , a n/2+2 , …, a n > Want the effect of bitonically sorting the sequence < a 1 , a 2 , …, a n/2, a n, a n-1, a n-2, ..., a n/2+1 >

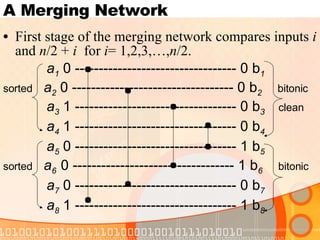
29. A Merging Network B ITONIC -S ORTER [n] compares inputs i and n /2+ i for i = 1,2,3,…, n /2. a 1 0 ---------------------------------- 0 b 1 a 2 0 ---------------------------------- 0 b 2 bitonic a 3 1 ---------------------------------- 0 b 3 clean bitonic a 4 1 ---------------------------------- 0 b 4 a 8 1 ---------------------------------- 1 b 8 a 7 0 ---------------------------------- 0 b 7 bitonic a 6 0 ---------------------------------- 1 b 6 a 5 0 ---------------------------------- 1 b 5

30. A Merging Network First stage of the merging network compares inputs i and n /2 + i for i = 1,2,3,…, n /2. a 1 0 ---------------------------------- 0 b 1 sorted a 2 0 ---------------------------------- 0 b 2 bitonic a 3 1 ---------------------------------- 0 b 3 clean a 4 1 ---------------------------------- 0 b 4 a 5 0 ---------------------------------- 1 b 5 sorted a 6 0 ---------------------------------- 1 b 6 bitonic a 7 0 ---------------------------------- 0 b 7 a 8 1 ---------------------------------- 1 b 8

31. A Merging Network Since the reversal of a bitonic sequence is bitonic sequence. Both top and bottom outputs from the first stage of the merging network satisfy the properties of Lemma 27.3 both the top half and the bottom half are bitonic every element in the top half is at least as small as every element in the bottom half at least one half is clean (either all 0’s or 1’s)

32. A Merging Network The top and bottom outputs can be bitonically sorted in parallel to produce the sorted output of the merging network.

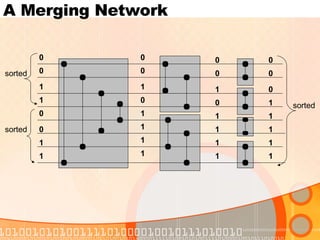
33. A Merging Network Bitonic- Sorter[n/2] Bitonic- Sorter[n/2]

34. A Merging Network 1 0 0 1 0 0 1 1 0 1 1 0 1 0 1 1 0 1 1 0 1 0 1 1 0 1 0 1 1 0 1 1 sorted sorted sorted

35. A Merging Network First stage is different Consequently the depth is the same as B ITONIC -S ORTER [n] Depth D(n) of M ERGER [n]: D(n) = { 0 if n =1, D(n/2) + 1 if n = 2 k and k>= 1 D(n) = lg n

36. A Sorting Network Now we have all the necessary tools to construct a network that can sort any input sequence We are going to use the a fore mentioned merging network to implement a parallel version of merge sort, called S ORTER [n]

37. A Sorting Network Sorter[n/2] Sorter[n/2] Merger[n]

38. A Sorting Network Merger[4] Merger[4] Merger[8] Merger[2] Merger[2] Merger[2] Merger[2]

39. A Sorting Network 1 0 1 0 1 0 0 0 0 0 1 1 0 0 0 1 0 1 0 0 0 0 1 1 0 1 0 1 0 1 0 0 1 depth 2 2 3 4 4 4 4 5 5 6

40. A Sorting Network

41. Conclusion Sorting Network Components Comparison Networks Zero-one Principle Bitonic Sorting Network Half-Cleaner Bitonic Sorter Merging Network Sorting Networks