This document describes a numerical study involving the solution of Poisson's equation using the finite volume method. It presents results from solving Laplace's equation on square domains with mixed boundary conditions, as well as solving the pressure Poisson equation derived from incompressible flow equations. Gaussian elimination, successive over-relaxation, and second-order accuracy are discussed. Numerical experiments demonstrate that over-relaxation improves convergence and the method achieves second-order accuracy based on grid refinement studies.

1. Programming Assignment 1
MECH 510 : Computational Methods in Transport
Phenomena
Solving the Poisson Equation
by
Shahzaib Malik
Student ID: 79974168
THE UNIVERSITY OF BRITISH COLUMBIA
(Vancouver)
October 2017
©Shahzaib Malik 2017
1

2. Contents
1 Introduction 3
2 Background and Methodology 4
3 Numerical Results 5
3.1 Point Gauss-Seidel iteration scheme . . . . . . . . . . . . . . . . . . . . . . . 6
3.2 Over-relaxation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
3.3 Convergence Behavior . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
3.4 Accuracy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
3.5 Poisson problem for pressure calculation for incompressible flows . . . . . . . 8
3.5.1 Solution order of accuracy for pressure problem . . . . . . . . . . . . . 10
3.5.2 Error bound in the solution value . . . . . . . . . . . . . . . . . . . . 10
4 Conclusion 11
5 Appendix 12
List of Figures
1 Square domain with mixed boundary conditions for Laplace problem . . . . . . 3
2 Solution error in each control volume for a 10×10 mesh . . . . . . . . . . . . 6
3 L norms of error and number of iterations required for 10×10 mesh . . . . . . 6
4 L norms of error and number of iterations required with over-relaxation for
10×10 mesh . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
5 Maximum change in solution at each iteration against iteration count for 20×20
mesh . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
6 L2 error norm in converged solution for different meshes . . . . . . . . . . . . 8
7 Four control volumes around (x,y) = 1
2, 1
2 . . . . . . . . . . . . . . . . . . . 9
8 Average solution value Px,y for different meshes . . . . . . . . . . . . . . . . 10
2

3. 1 Introduction
This exercise involves solving the Poisson equation using the cell-centered finite volume method
in the square domain that has mixed boundary conditions. The Poisson equation can be derived
from incompressible energy equation by making the assumptions of steady-state and zero ve-
locity (refer [2] for complete derivation). For a two-dimensional case, the Poisson equation
which is an elliptic partial differential equation can be expressed as follow:
∂2T
∂x2
+
∂2T
∂y2
= S (1.1)
with S being the source term
The exercise is divided into two problems. In this first case, there is no source term and so
the Poisson equation reduces to Laplace equation and the exact solution to this equation can be
represented by equation 1.2:
T(x,y) =
cos(πx)sinh(πy)
sinhπ
(1.2)
The boundary conditions for this case are as shown below.
Figure 1: Square domain with mixed boundary conditions for Laplace problem
However, the second case has a source term and it is an application of the Poisson problem
that calculates pressure for incompressible flows. Therefore, the code from first part had to be
modified to include the source term that can be derived by substituting the provided velocities
into equation 1.3. The velocities are as follow:
u = x3
−3xy2
v = −3x2
y+y3
Substituting the velocities into below equation:
3

4. ∂2P
∂x2
+
∂2P
∂y2
= −
∂u
∂x
2
+2
∂v
∂x
∂u
∂y
+
∂u
∂y
2
(1.3)
leads to the source term (used for second problem) below:
∇2
P = − 18x4
+18y4
+36x2
y2
(1.4)
The boundary conditions for pressure problem are ∂P
∂n = 0 at x = 0 and y = 0 while P = 5 −
1
2 (1+y)3
when x = 1and P = 5− 1
2 1+x2 3
for y = 1.
2 Background and Methodology
The point Gauss-Seidel iteration scheme can be written as follow [2]:
T
k+1
i,j =
∆y2
2(∆x2 +∆y2)
T
k
i+1,j +T
k+1
i−1,j +
∆x2
2(∆x2 +∆y2)
T
k
i,j+1 +T
k+1
i,j−1 −Si,j
∆x2∆y2
2(∆x2 +∆y2)
(2.1)
This scheme is much more efficient than point Jacobi iteration scheme and uses less storage
as the latest available data can be used unlike the point Jacobi method that requires more stor-
age (refer [2] for details on Jacobi method). Moreover, careful observation of these iteration
schemes lead to the conclusion that the solution update is always less than it should be and
as so a sensible thing will be to increase this solution update by some factor. Updating the
Gauss-Seidel iteration scheme by some factor can result in the following scheme:
δk+1
i,j =
∆y2
2(∆x2 +∆y2)
T
k
i+1,j +T
k+1
i−1,j +
∆x2
2(∆x2 +∆y2)
T
k
i,j+1 +T
k+1
i,j−1 −Si,j
∆x2∆y2
2(∆x2 +∆y2)
−T
k
i,j
T
k+1
i,j = T
k
i,j +ωδk+1
i,j (2.2)
The above iteration scheme is then known as the successive over-relaxation (SOR). In this exer-
cise, this form of the Gauss-Seidel method was used to solve the system of linear equations. The
SOR method is usually used in numerical linear algebra to enable faster convergence and was
originally introduced to automate the process of solving linear equations on digital computers.
4

5. It must be noted here from above equations that ω = 1 means no over-relaxation. Furthermore,
the stability of successive over-relaxation scheme required ω to be less than two.
There were two types of boundary conditions used known as the Dirichlet and Neumann bound-
ary conditions. These boundary conditions were enforced using the ghost cells which help to
correctly enforce boundary conditions without effecting the solution as they lie outside the com-
putational domain, meaning any solution value assigned to these cells should be just imaginary.
These imaginary solution values were calculated by making use of linear extrapolation [2].
For Dirichlet boundary condition and ghost cell, we have:
Ta,b = 2Tw −Ti,j (2.3)
where,
Ta,b =value of T in a ghost cell at Dirichlet boundary where a,b depends on position of ghost
cell from cell i, j.
Tw =value of T at the boundary next to ghost cell
Ti,j =value of T in cell i, j that is just next to ghost cell
For Neumann boundary condition and ghost cell we have:
Tc,d = Ti,j +c
∂T
∂n
∆ f (2.4)
where,
Tc,d =value of T in a ghost cell at Neumann boundary where c,d again depends on position
of ghost cell from cell i, j
Ti,j =value of T in cell i, j that is just next to ghost cell
c = +1 or −1 depending on where ghost cell is from cell i, j
∂T
∂n
=value at boundary next to ghost cell
∆ f = ∆x or ∆y depending on the direction in which linear extrapolation needs to be carried
out
3 Numerical Results
This section presents the results in a sequence following the handout.
5

6. 3.1 Point Gauss-Seidel iteration scheme
The program was run to solve the Laplace problem on a 10×10 mesh without successive over-
relaxation. Here the Gauss-Seidel routine was used and iteration carried out until the maximum
in solution reached to order of 10−9(which is much less than 10−7). The solution error was then
plotted as shown in figure 2 below:
Figure 2: Solution error in each control volume for a 10×10 mesh
Moreover, the number of iterations required and L norms of error in the converged solution
were recorded in figure 3 below:
ω L1 L2 L∞ Final max. change in solution Number of iterations
1.0 1.250×10−3 2.456×10−3 9.096×10−3 9.856×10−9 258
Figure 3: L norms of error and number of iterations required for 10×10 mesh
3.2 Over-relaxation
The Gauss-Seidel subroutine was then modified in order to do successive over-relaxation and
the SOR parameter ω was set equal to 1.5. The L norms of error and number of iterations were
then recorded again and presented in figure 4 below:
6

7. ω L1 L2 L∞ Final max. change in solution Number of iterations
1.5 1.250×10−3 2.456×10−3 9.096×10−3 9.595×10−9 108
Figure 4: L norms of error and number of iterations required with over-relaxation for 10 × 10
mesh
It can be observed that the L norms of error remained same while the number iterations dropped
significantly as a result of over-relaxation. Therefore, as expected and discussed above, the
successive over-relaxation helped to converge the solution faster.
3.3 Convergence Behavior
The next step was then to test the convergence behavior and a 20 × 20 mesh was used for this
and the program was run to steady state at three different values of ω. For each value of ω,
the desired final change in solution was set to be smaller than 10−8. The maximum change in
solution was then plotted against the number of iterations in figure 5 :
Figure 5: Maximum change in solution at each iteration against iteration count for 20×20 mesh
It can seen from the above figure that as the value of ω was increased from 1 to 1.5, the solution
started to converge faster and less number of iterations were required to achieve the desired
convergence criteria for the solution. This means that successive over-relaxation method suc-
cessfully helped to converge solution faster which was expected.
7

8. 3.4 Accuracy
The order of accuracy of the code was tested by running it for four different meshes and L2
error norm in solution was recorded in figure 6 for each mesh size.
Mesh ∆x ∆y L2 ratio (L2)width=2h
(L2)width=h
10×10 0.1 0.1 2.456×10−3 −
20×20 0.05 0.05 6.386×10−4 3.846
40×40 0.025 0.025 1.612×10−4 3.962
80×80 0.0125 0.0125 4.050×10−5 3.980
Figure 6: L2 error norm in converged solution for different meshes
For a two-dimensional case, the error for p−th order accurate method is given by:
E ∼ c1∆xp
+c2∆yp
= chp
Taking logarithm on both sides lead to:
log E = p log h+log c (3.1)
Equation 3.1 above is the equation of straight line with slope p which can be evaluated using
the L2 error norm as follow:
p =
log (L2)width=2h
(L2)width=h
log 2
=
log(3.980)
log 2
= 1.9927 ≈ 2.0
The ratio between the two finest meshes was considered as that should provide the most accurate
result. Since the value of p is almost 2 so it can be concluded the the numerical method used in
this case is second-order accurate.
3.5 Poisson problem for pressure calculation for incompressible flows
We then solved the Poisson problem for pressure and the code from first part was modified to
include the source term and boundary conditions were changed as mentioned above. The goal
was to approximate the value of solution P at (x,y) = 1
2, 1
2 and this point was exactly at the
middle of square domain. The average of pressure at this point was calculated by taking into
account control volumes surrounding this point and carrying out the interpolation. The accuracy
8

9. of solution depends on number of control volumes taken into account and it turned out that if
only two control volumes were chosen, the solution was first-order accurate. However, since we
want our solution to be second-order accurate like in the first problem so four control volumes
around 1
2, 1
2 were taken into account as shown in figure 7.
Figure 7: Four control volumes around (x,y) = 1
2, 1
2
Then , the Taylor series expansion around this point for each control volume gave:
PCV1 = Px,y −
∂P
∂x
x,y
∆x
2
+
∂P
∂y
x,y
∆y
2
+
∂2P
∂x2
x,y
∆x2
6
+
∂2P
∂x∂y
x,y
∆x∆y
4
+
∂2P
∂y2
x,y
∆y2
6
+......
PCV2 = Px,y +
∂P
∂x
x,y
∆x
2
+
∂P
∂y
x,y
∆y
2
+
∂2P
∂x2
x,y
∆x2
6
+
∂2P
∂x∂y
x,y
∆x∆y
4
+
∂2P
∂y2
x,y
∆y2
6
+......
PCV3 = Px,y −
∂P
∂x
x,y
∆x
2
−
∂P
∂y
x,y
∆y
2
+
∂2P
∂x2
x,y
∆x2
6
−
∂2P
∂x∂y
x,y
∆x∆y
4
+
∂2P
∂y2
x,y
∆y2
6
+......
PCV1 = Px,y +
∂P
∂x
x,y
∆x
2
−
∂P
∂y
x,y
∆y
2
+
∂2P
∂x2
x,y
∆x2
6
−
∂2P
∂x∂y
x,y
∆x∆y
4
+
∂2P
∂x2
x,y
∆x2
6
+......
9

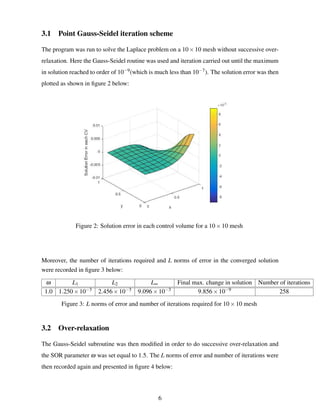
10. The average value of P at the center point was then evaluated as follow:
Px,y =
PCV1 +PCV1 +PCV1 +PCV1
4
= Px,y +
∂2P
∂x2
x,y
∆x2
6
+
∂2P
∂y2
x,y
∆y2
6
Px,y = Px,y +O(∆x2
,∆y2
)
Clearly, the above value Px,y is second-order accurate.
3.5.1 Solution order of accuracy for pressure problem
Using the above concept, the value of Px,y at (x,y) = 1
2, 1
2 was then obtained using the code
for a range of meshes and Richardson extrapolation used to get the observed order of accuracy.
The desired or final maximum change in solution was set to 10−9 for all the cases. These values
for different meshes are listed below:
Mesh Px,y
1 20×20 4.93848605706
2 40×40 4.93774397185
3 80×80 4.93754900167
Figure 8: Average solution value Px,y for different meshes
The Richardson extrapolation says that the observed order of accuracyp of the solution is
given by:
p =
log


P(x,y)
1
−P(x,y)
2
P(x,y)
2
−P(x,y)
3


log2
= 1.928 ≈ 2.0
Therefore, the observed order of accuracy suggests that the numerical method is second-order
accurate.
3.5.2 Error bound in the solution value
The ASME solution accuracy handout says that the extrapolated approximation to exact solution
is given by [1]:
10

11. Pexact ≈
2p P(x,y)
3
−P(x,y)
2
2p −1
= 4.937484012
The error bound can now be calculated by comparing Pexact with the value P(x,y) from the finest
mesh above as follow:
Error =
P(x,y)
3
−Pexact
P(x,y)
3
×100% = 0.0013%
4 Conclusion
The Poisson equation was solved successfully for two cases (with and without the source term)
using the finite volume scheme. The system of linear equations was first solved using the
Point Gauss-Seidel iteration scheme and then this was modified to enforce the successive over-
relaxation method. The effect of performing over-relaxation was studied by converging the
solution to steady-state for a sequence of meshes and faster solution convergence in case of
over-relaxation clearly highlighted the advantage of SOR method in terms of computational
cost and time. Moreover, for both the problems, it was proved that the solution is second order
accurate. For the second problem, the solution was first computed for a sequence of meshes and
Richardson extrapolation was used that gave us estimate of the order of accuracy. This order
of accuracy was then used to calculate the exact solution as mentioned in ASME handout. The
exact solution and numerical solution from the finest mesh were then compared at (x,y) = 1
2, 1
2
and error was calculated which was small enough for our numerical solution to be considered
accurate.
References
[1] Patrick J.Roache Ismail B. Celik, Urmila Ghia and Christopher J.Freitas. Statement on the
control of numerical accuracy. ASME JOURNAL OF FLUIDS ENGINEERING, 1986.
[2] Carl Ollivier-Gooch. MECH 510 Course notes: Computational Methods in Transport Phe-
nomena. UBC Department of Mechanical Engineering.
11

12. 5 Appendix
Below are some main points about the program
Laplace Problem
The inputs in this case are as follow:
• dmax_change : this is desired maximum change in solution
• Omega ω : A parameter in SOR equation
• i_cells : number of control volumes in i-direction (horizontal direction)
• j_cells : number of control volumes in j-direction (vertical direction)
The Laplace problem runs with above inputs and if the solution converges, the corresponding
message prints out.
Furthermore, following outputs can be obtained:
• Iteration number and corresponding maximum change in solution
• The L norms of error in the solution
• Solution error in each control. The program also outputs a file (solutionError.txt) that
was used to get surface plot in MATLAB
• The total number of iterations and final maximum change in solution
12

13. Pressure Problem
The inputs in this case were same as for above problem. However, we have a source term and
different boundary conditions as explained above in the report.
The Pressure problem runs with above inputs and if the solution converges, the corresponding
message prints out.
Furthermore, the following outputs can be obtained:
• Iteration number and corresponding maximum change in solution
• Solution value P at x = y = 0.5
• Average over four CV solution value P at x = y = 0.5
• The total number of iterations and final maximum change in solution
13