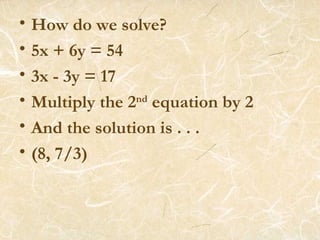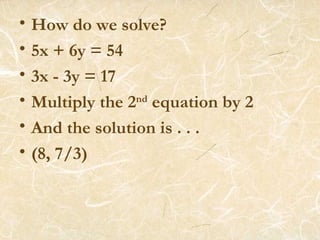
This document discusses solving systems of equations by elimination. It provides examples of eliminating a variable by adding or subtracting equations. The key steps are: 1) write the equations in standard form; 2) add or subtract the equations to eliminate one variable; 3) substitute the eliminated variable back into one equation to solve for the other variable. Checking the solution in both original equations verifies the correct solution was found.

1. Solving Systems By Elimination

2. Both equations must be in standard form. The goal is to eliminate one of the variables. You can add or subtract the equations to eliminate .

3. Solve the system by elimination: 5x – 6y = -32 3x + 6y = 48 8x = 16 x = 2 Line these two equations up. Look to if any of the variables would cancel each other out if the two equations were added or subtracted.

4. Substitute the x back into one of the equations to find the other variable. 5(2) – 6y = -32 y = 7 The point of intersection is (2, 7)

5. Check your work. Does the point work in both equations?

6. How do we solve? x + y = 6 x + 3y = 10 Subtract (or multiply 2 nd equation by -1) And the solution is . . . (4, 2)

7. How do we solve? 5x + 6y = 54 3x - 3y = 17 Multiply the 2 nd equation by 2 And the solution is . . . (8, 7/3)

8. How do we solve? -a + 2b = -1 a = 3b - 1 1 st , get that 2 nd equation in standard form. a – 3b = -1 And the solution is . . . (5, 2)

9. How do we solve? 2k – 3c = 6 6k – 9c = 9 Multiply 1 st row by -3. And the solution is . . . No solution What do you notice that helps you understand this is no solution?

10. How do we solve? x + 4y = 1 3x + 12y = 3 Multiply the 1 st one by -3 And the solution is . . . Infinite number of solutions What do you notice that helps you understand this is infinite number of solutions?