Cristiano Longo, profile picture
Uploaded byCristiano Longo
PDF, PPTX649 views

Adding Semantics to Ontologies

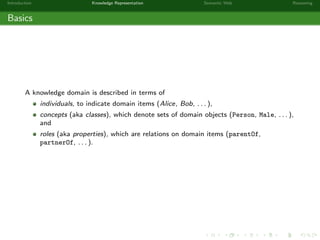
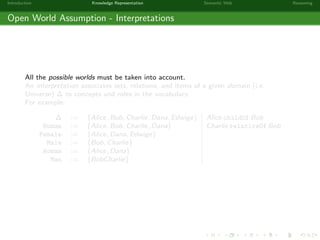
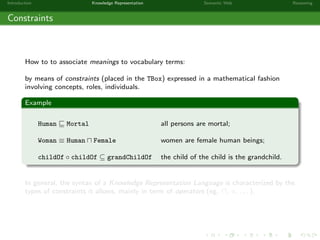
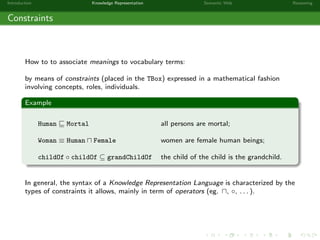
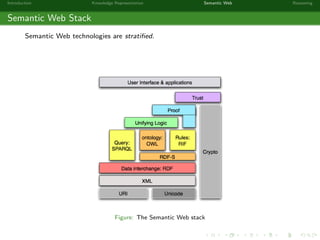
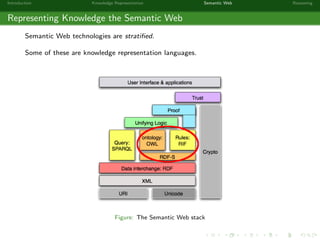
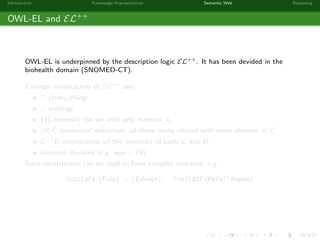
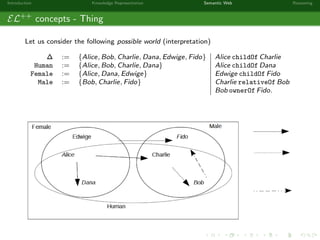
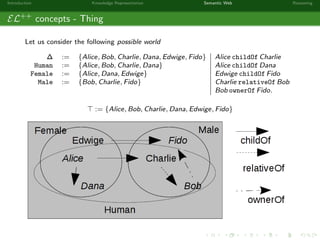
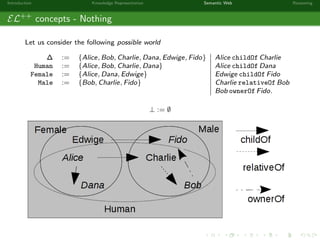
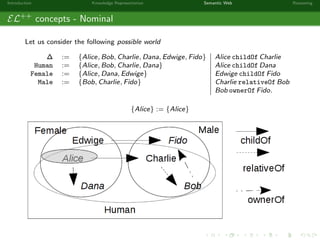
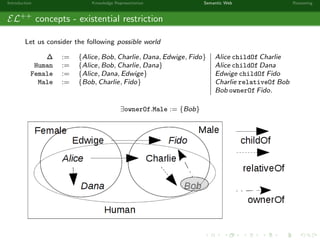
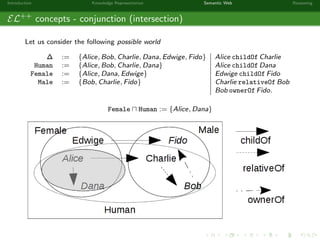
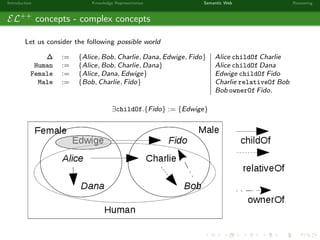
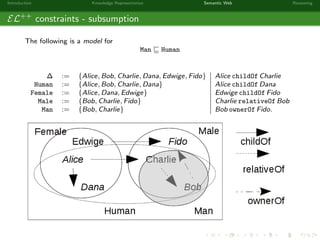
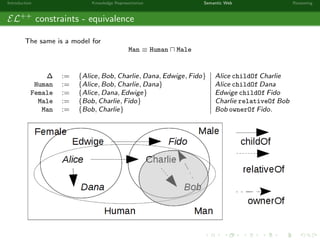
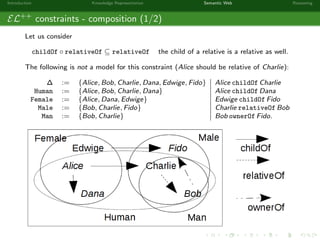
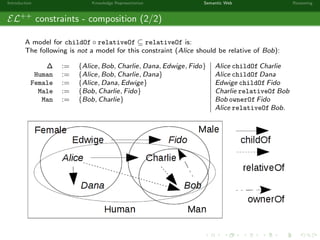
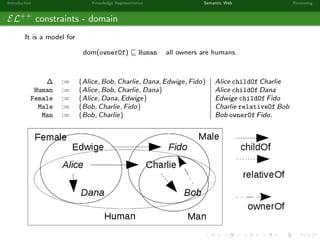
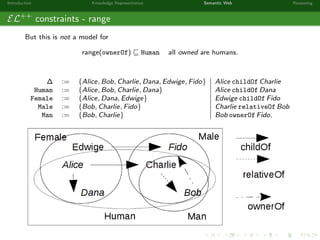
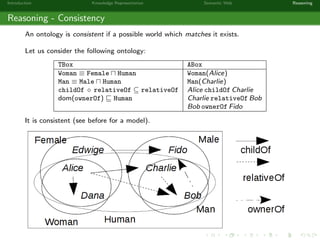
This document provides an introduction to knowledge representation and the semantic web. It discusses how ontologies can be used to represent knowledge through concepts, individuals, and roles. It also describes how the semantic web framework, particularly OWL and its subprofile OWL-EL, provides tools to represent knowledge formally using description logics. Key topics covered include ontologies, the open world assumption, vocabulary and assertions, constraints to define meanings of terms, and how semantic web technologies like OWL can be used to represent knowledge in a formal, logical way.

Science◦
Related topics:
Semantic Web•

Embed presentation

Download as PDF, PPTX
Introduction Knowledge Representation Semantic Web Reasoning Adding Semantics to Ontologies Cristiano Longo Dipartimento di Matematica e Informatica, Universit`a di Catania, Italy mailto://longo@dmi.unict.it SOD2014
Introduction Knowledge Representation Semantic Web Reasoning About This talk is about the word Semantic in the “Semantic Web.” It will provides some basic theoretical notions for a better understanding of Semantic Web technologies (in particular OWL).
Introduction Knowledge Representation Semantic Web Reasoning Topics Some answers for the following questions will be provided: How can we represent knowledge? (ontologies) Which tools the Semantic Web framework offer to this end? (OWL) How representing knowledge with these tools can be useful? (reasoning)
Introduction Knowledge Representation Semantic Web Reasoning Topics Some answers for the following questions will be provided: How can we represent knowledge? (ontologies) Which tools the Semantic Web framework offer to this end? (OWL) How representing knowledge with these tools can be useful? (reasoning)
Introduction Knowledge Representation Semantic Web Reasoning Topics Some answers for the following questions will be provided: How can we represent knowledge? (ontologies) Which tools the Semantic Web framework offer to this end? (OWL) How representing knowledge with these tools can be useful? (reasoning)
Introduction Knowledge Representation Semantic Web Reasoning Notice For the sake of readability and for historical reason, we will use notation and terminology from Descriptio Logics, which underpin Semantic Web languages (in particular OWL).
Introduction Knowledge Representation Semantic Web Reasoning Representing Knowledge in Logic and Computer Science
Introduction Knowledge Representation Semantic Web Reasoning Ontologies An ontology is a (partial) description of the world. Usually, it is a finite set of statements such as, for example, human beings are mortals, Alice is the Bob’s mother, Federico II was an emperor.
Introduction Knowledge Representation Semantic Web Reasoning Basics A knowledge domain is described in terms of individuals, to indicate domain items (Alice, Bob, . . . ), concepts (aka classes), which denote sets of domain objects (Person, Male, . . . ), and roles (aka properties), which are relations on domain items (parentOf, partnerOf, . . . ).
Introduction Knowledge Representation Semantic Web Reasoning Vocabulary and Assertions Each ontology is divided into two parts: the TBox(vocabulary), in which vocabulary terms for concepts (i.e. sets) and roles (i.e. relations) are defined, and the ABox, which contains statements (namely, assertions) about real world items. TBox Concepts: Male, Female,Human,Woman, Man. Roles: relativeOf, childOf, grandChildOf. ABox Woman(Alice), Man(Bob), Alice relativeOf Bob, Alice childOf Charlie.
Introduction Knowledge Representation Semantic Web Reasoning Vocabulary and Assertions Each ontology is divided into two parts: the TBox(vocabulary), in which vocabulary terms for concepts (i.e. sets) and roles (i.e. relations) are defined, and the ABox, which contains statements (namely, assertions) about real world items. TBox Concepts: Male, Female,Human,Woman, Man. Roles: relativeOf, childOf, grandChildOf. ABox Woman(Alice), Man(Bob), Alice relativeOf Bob, Alice childOf Charlie.
Introduction Knowledge Representation Semantic Web Reasoning Open World Assumption Facts not explicitly mentioned in the ontology are not assumed to be false, their truth value is just unknown. In general, no one has complete knowledge. TBox Concepts: Male, Female,Human,Woman, Man. Roles: relativeOf, childOf, grandChildOf. ABox Woman(Alice), Man(Bob), Alice relativeOf Bob, Alice childOf Charlie. What is the kinship relation between Alice and Bob? Charlie childOf Alice? Is Charlie a man? Is Charlie a human being? What about other persons in the world?
Introduction Knowledge Representation Semantic Web Reasoning Open World Assumption Facts not explicitly mentioned in the ontology are not assumed to be false, their truth value is just unknown. In general, no one has complete knowledge. TBox Concepts: Male, Female,Human,Woman, Man. Roles: relativeOf, childOf, grandChildOf. ABox Woman(Alice), Man(Bob), Alice relativeOf Bob, Alice childOf Charlie. What is the kinship relation between Alice and Bob? Charlie childOf Alice? Is Charlie a man? Is Charlie a human being? What about other persons in the world?
Introduction Knowledge Representation Semantic Web Reasoning Open World Assumption - Interpretations All the possible worlds must be taken into account. An interpretation associates sets, relations, and items of a given domain (i.e. Universe) ∆ to concepts and roles in the vocabulary. For example: ∆ := {Alice, Bob, Charlie, Dana, Edwige} Alice childOf Bob Human := {Alice, Bob, Charlie, Dana} Charlie relativeOf Bob Female := {Alice, Dana, Edwige} Male := {Bob, Charlie} Woman := {Alice, Dana} Man := {BobCharlie}
Introduction Knowledge Representation Semantic Web Reasoning Open World Assumption - Interpretations All the possible worlds must be taken into account. An interpretation associates sets, relations, and items of a given domain (i.e. Universe) ∆ to concepts and roles in the vocabulary. For example: ∆ := {Alice, Bob, Charlie, Dana, Edwige} Alice childOf Bob Human := {Alice, Bob, Charlie, Dana} Charlie relativeOf Bob Female := {Alice, Dana, Edwige} Male := {Bob, Charlie} Woman := {Alice, Dana} Man := {BobCharlie}
Introduction Knowledge Representation Semantic Web Reasoning Open World Assumption - Interpretations All the possible worlds must be taken into account. An interpretation associates sets, relations, and items of a given domain (i.e. Universe) ∆ to concepts and roles in the vocabulary. For example: ∆ := {Alice, Bob, Charlie, Dana, Edwige} Alice childOf Bob Human := {Alice, Bob, Charlie, Dana} Charlie relativeOf Bob Female := {Alice, Dana, Edwige} Male := {Bob, Charlie} Woman := {Alice, Dana} Man := {BobCharlie}
Introduction Knowledge Representation Semantic Web Reasoning Open World Assumption - Models (1/2) Roughly speaking, an interpretation is a model for an ontology if it does not contradicts the ontology itself For example: ∆ := {Alice, Bob, Charlie, Dana, Edwige} Alice childOf Charlie Human := {Alice, Bob, Charlie, Dana} Charlie relativeOf Bob Female := {Alice, Dana, Edwige} Male := {Bob, Charlie} Woman := {Alice, Dana} Man := {BobCharlie} is a model for TBox Concepts: Male, Female,Human,Woman, Man. Roles: relativeOf, childOf, grandChildOf. ABox Woman(Alice), Man(Bob), Alice relativeOf Bob, Alice childOf Charlie.
Introduction Knowledge Representation Semantic Web Reasoning Open World Assumption - Models (2/2) Wherease the following is not. ∆ := {Alice, Bob, Charlie, Dana, Edwige} Alice relativeOf Charlie Human := {Alice, Bob, Charlie, Dana} Charlie relativeOf Bob Female := {Alice, Dana, Edwige} Male := {Bob, Charlie} Woman := {Alice, Dana} Man := {BobCharlie} TBox Concepts: Male, Female,Human,Woman, Man. Roles: relativeOf, childOf, grandChildOf. ABox Woman(Alice), Man(Bob), Alice relativeOf Bob, Alice childOf Charlie.
Introduction Knowledge Representation Semantic Web Reasoning Constraints How to to associate meanings to vocabulary terms: by means of constraints (placed in the TBox) expressed in a mathematical fashion involving concepts, roles, individuals. Example Human Mortal all persons are mortal; Woman ≡ Human Female women are female human beings; childOf ◦ childOf ⊆ grandChildOf the child of the child is the grandchild. In general, the syntax of a Knowledge Representation Language is characterized by the types of constraints it allows, mainly in term of operators (eg. , ◦, . . . ).
Introduction Knowledge Representation Semantic Web Reasoning Constraints How to to associate meanings to vocabulary terms: by means of constraints (placed in the TBox) expressed in a mathematical fashion involving concepts, roles, individuals. Example Human Mortal all persons are mortal; Woman ≡ Human Female women are female human beings; childOf ◦ childOf ⊆ grandChildOf the child of the child is the grandchild. In general, the syntax of a Knowledge Representation Language is characterized by the types of constraints it allows, mainly in term of operators (eg. , ◦, . . . ).
Introduction Knowledge Representation Semantic Web Reasoning Representing Knowledge the Semantic Web
Introduction Knowledge Representation Semantic Web Reasoning Semantic Web Stack Semantic Web technologies are stratified. Figure: The Semantic Web stack
Introduction Knowledge Representation Semantic Web Reasoning Representing Knowledge the Semantic Web Semantic Web technologies are stratified. Some of these are knowledge representation languages. Figure: The Semantic Web stack
Introduction Knowledge Representation Semantic Web Reasoning OWL OWL is the concise name of the Web Ontology Language, currently at version 2. http://www.w3.org/TR/2012/REC-owl2-primer-20121211/ Three different profiles (fragments) have been defined for it (see http://www.w3.org/TR/2012/REC-owl2-profiles-20121211/): OWL-RL quite good expressive power; OWL-QL for large ABox; OWL-EL very efficient, also in presence of large TBox. Here we consider OWL-EL.
Introduction Knowledge Representation Semantic Web Reasoning OWL OWL is the concise name of the Web Ontology Language, currently at version 2. http://www.w3.org/TR/2012/REC-owl2-primer-20121211/ Three different profiles (fragments) have been defined for it (see http://www.w3.org/TR/2012/REC-owl2-profiles-20121211/): OWL-RL quite good expressive power; OWL-QL for large ABox; OWL-EL very efficient, also in presence of large TBox. Here we consider OWL-EL.
Introduction Knowledge Representation Semantic Web Reasoning OWL-EL and EL++ OWL-EL is underpinned by the description logic EL++. It has been devided in the biohealth domain (SNOMED-CT). Concept constructors of EL++ are: (every)thing; ⊥ nothing; {a} nominal, the set with only member a; ∃R.C existential restriction, all those items related with some element in C; C D conjunction, all the members of both C and D; concrete domains (e.g. age > 18). Such constructors can be used to form complex concepts, e.g. ∃childOf.{Fido} := {Edwige}, ∃childOf.(Male Human).
Introduction Knowledge Representation Semantic Web Reasoning OWL-EL and EL++ OWL-EL is underpinned by the description logic EL++. It has been devided in the biohealth domain (SNOMED-CT). Concept constructors of EL++ are: (every)thing; ⊥ nothing; {a} nominal, the set with only member a; ∃R.C existential restriction, all those items related with some element in C; C D conjunction, all the members of both C and D; concrete domains (e.g. age > 18). Such constructors can be used to form complex concepts, e.g. ∃childOf.{Fido} := {Edwige}, ∃childOf.(Male Human).
Introduction Knowledge Representation Semantic Web Reasoning OWL-EL and EL++ OWL-EL is underpinned by the description logic EL++. It has been devided in the biohealth domain (SNOMED-CT). Concept constructors of EL++ are: (every)thing; ⊥ nothing; {a} nominal, the set with only member a; ∃R.C existential restriction, all those items related with some element in C; C D conjunction, all the members of both C and D; concrete domains (e.g. age > 18). Such constructors can be used to form complex concepts, e.g. ∃childOf.{Fido} := {Edwige}, ∃childOf.(Male Human).
Introduction Knowledge Representation Semantic Web Reasoning EL++ concepts - Thing Let us consider the following possible world (interpretation) ∆ := {Alice, Bob, Charlie, Dana, Edwige, Fido} Alice childOf Charlie Human := {Alice, Bob, Charlie, Dana} Alice childOf Dana Female := {Alice, Dana, Edwige} Edwige childOf Fido Male := {Bob, Charlie, Fido} Charlie relativeOf Bob Bob ownerOf Fido.
Introduction Knowledge Representation Semantic Web Reasoning EL++ concepts - Thing Let us consider the following possible world ∆ := {Alice, Bob, Charlie, Dana, Edwige, Fido} Alice childOf Charlie Human := {Alice, Bob, Charlie, Dana} Alice childOf Dana Female := {Alice, Dana, Edwige} Edwige childOf Fido Male := {Bob, Charlie, Fido} Charlie relativeOf Bob Bob ownerOf Fido. := {Alice, Bob, Charlie, Dana, Edwige, Fido}
Introduction Knowledge Representation Semantic Web Reasoning EL++ concepts - Nothing Let us consider the following possible world ∆ := {Alice, Bob, Charlie, Dana, Edwige, Fido} Alice childOf Charlie Human := {Alice, Bob, Charlie, Dana} Alice childOf Dana Female := {Alice, Dana, Edwige} Edwige childOf Fido Male := {Bob, Charlie, Fido} Charlie relativeOf Bob Bob ownerOf Fido. ⊥ := ∅
Introduction Knowledge Representation Semantic Web Reasoning EL++ concepts - Nominal Let us consider the following possible world ∆ := {Alice, Bob, Charlie, Dana, Edwige, Fido} Alice childOf Charlie Human := {Alice, Bob, Charlie, Dana} Alice childOf Dana Female := {Alice, Dana, Edwige} Edwige childOf Fido Male := {Bob, Charlie, Fido} Charlie relativeOf Bob Bob ownerOf Fido. {Alice} := {Alice}
Introduction Knowledge Representation Semantic Web Reasoning EL++ concepts - existential restriction Let us consider the following possible world ∆ := {Alice, Bob, Charlie, Dana, Edwige, Fido} Alice childOf Charlie Human := {Alice, Bob, Charlie, Dana} Alice childOf Dana Female := {Alice, Dana, Edwige} Edwige childOf Fido Male := {Bob, Charlie, Fido} Charlie relativeOf Bob Bob ownerOf Fido. ∃ownerOf.Male := {Bob}
Introduction Knowledge Representation Semantic Web Reasoning EL++ concepts - conjunction (intersection) Let us consider the following possible world ∆ := {Alice, Bob, Charlie, Dana, Edwige, Fido} Alice childOf Charlie Human := {Alice, Bob, Charlie, Dana} Alice childOf Dana Female := {Alice, Dana, Edwige} Edwige childOf Fido Male := {Bob, Charlie, Fido} Charlie relativeOf Bob Bob ownerOf Fido. Female Human := {Alice, Dana}
Introduction Knowledge Representation Semantic Web Reasoning EL++ concepts - complex concepts Let us consider the following possible world ∆ := {Alice, Bob, Charlie, Dana, Edwige, Fido} Alice childOf Charlie Human := {Alice, Bob, Charlie, Dana} Alice childOf Dana Female := {Alice, Dana, Edwige} Edwige childOf Fido Male := {Bob, Charlie, Fido} Charlie relativeOf Bob Bob ownerOf Fido. ∃childOf.{Fido} := {Edwige}
Introduction Knowledge Representation Semantic Web Reasoning EL++ constraints Constraints allowed in EL++ TBox are of the types: C D every member of C is a member of D as well; C ≡ D the sets C and D coincide; R1 ◦ . . . ◦ Rn S the composition of R1, . . . , Rn is a subrelation of S; dom(R) C if x is related to y by R, then x must be a member of C; range(R) C if x is related to y by R, then y must be a member of C.
Introduction Knowledge Representation Semantic Web Reasoning EL++ constraints - subsumption The following is a model for Man Human ∆ := {Alice, Bob, Charlie, Dana, Edwige, Fido} Alice childOf Charlie Human := {Alice, Bob, Charlie, Dana} Alice childOf Dana Female := {Alice, Dana, Edwige} Edwige childOf Fido Male := {Bob, Charlie, Fido} Charlie relativeOf Bob Man := {Bob, Charlie} Bob ownerOf Fido.
Introduction Knowledge Representation Semantic Web Reasoning EL++ constraints - equivalence The same is a model for Man ≡ Human Male ∆ := {Alice, Bob, Charlie, Dana, Edwige, Fido} Alice childOf Charlie Human := {Alice, Bob, Charlie, Dana} Alice childOf Dana Female := {Alice, Dana, Edwige} Edwige childOf Fido Male := {Bob, Charlie, Fido} Charlie relativeOf Bob Man := {Bob, Charlie} Bob ownerOf Fido.
Introduction Knowledge Representation Semantic Web Reasoning EL++ constraints - composition (1/2) Let us consider childOf ◦ relativeOf ⊆ relativeOf the child of a relative is a relative as well. The following is not a model for this constraint (Alice should be relative of Charlie): ∆ := {Alice, Bob, Charlie, Dana, Edwige, Fido} Alice childOf Charlie Human := {Alice, Bob, Charlie, Dana} Alice childOf Dana Female := {Alice, Dana, Edwige} Edwige childOf Fido Male := {Bob, Charlie, Fido} Charlie relativeOf Bob Man := {Bob, Charlie} Bob ownerOf Fido.
Introduction Knowledge Representation Semantic Web Reasoning EL++ constraints - composition (2/2) A model for childOf ◦ relativeOf ⊆ relativeOf is: The following is not a model for this constraint (Alice should be relative of Bob): ∆ := {Alice, Bob, Charlie, Dana, Edwige, Fido} Alice childOf Charlie Human := {Alice, Bob, Charlie, Dana} Alice childOf Dana Female := {Alice, Dana, Edwige} Edwige childOf Fido Male := {Bob, Charlie, Fido} Charlie relativeOf Bob Man := {Bob, Charlie} Bob ownerOf Fido Alice relativeOf Bob.
Introduction Knowledge Representation Semantic Web Reasoning EL++ constraints - domain It is a model for dom(ownerOf) Human all owners are humans. ∆ := {Alice, Bob, Charlie, Dana, Edwige, Fido} Alice childOf Charlie Human := {Alice, Bob, Charlie, Dana} Alice childOf Dana Female := {Alice, Dana, Edwige} Edwige childOf Fido Male := {Bob, Charlie, Fido} Charlie relativeOf Bob Man := {Bob, Charlie} Bob ownerOf Fido.
Introduction Knowledge Representation Semantic Web Reasoning EL++ constraints - range But this is not a model for range(ownerOf) Human all owned are humans. ∆ := {Alice, Bob, Charlie, Dana, Edwige, Fido} Alice childOf Charlie Human := {Alice, Bob, Charlie, Dana} Alice childOf Dana Female := {Alice, Dana, Edwige} Edwige childOf Fido Male := {Bob, Charlie, Fido} Charlie relativeOf Bob Man := {Bob, Charlie} Bob ownerOf Fido.
Introduction Knowledge Representation Semantic Web Reasoning Using Knowledge encoded in EL++
Introduction Knowledge Representation Semantic Web Reasoning Reasoning Defining a formal semantics enables some reasoning task to be performed automatically. Here we will see consistency checking, to check the absence of logical errors, inferencing, to extract hidden knowledge.
Introduction Knowledge Representation Semantic Web Reasoning Reasoning - Consistency An ontology is consistent if a possible world which matches it exists. Let us consider the following ontology: TBox ABox Woman ≡ Female Human Woman(Alice) Man ≡ Male Human Man(Charlie) childOf ◦ relativeOf ⊆ relativeOf Alice childOf Charlie dom(ownerOf) Human Charlie relativeOf Bob Bob ownerOf Fido It is consistent (see before for a model).
Introduction Knowledge Representation Semantic Web Reasoning Reasoning - Consistency - example 2 The following one is not consistent. TBox ABox Woman ≡ Female Human Woman(Alice) Man ≡ Male Human Man(Charlie) childOf ◦ relativeOf ⊆ relativeOf Alice childOf Charlie dom(ownerOf) Human Charlie relativeOf Bob Male Female ≡ ⊥ Bob ownerOf Fido Female(Bob) Bob must be Male, as it is a Man, all men are Male and Male and Female are disjoint.
Introduction Knowledge Representation Semantic Web Reasoning Reasoning - Consistency - example 3 The following one is not consistent. TBox ABox Woman ≡ Female Human Woman(Alice) Man ≡ Male Human Man(Charlie) childOf ◦ relativeOf ⊆ relativeOf Alice childOf Charlie dom(ownerOf) Human Charlie relativeOf Bob Human Edwige ≡ ⊥ Bob ownerOf Fido Edwige ownerOf Fido Edwige can’t be the owner of Fido because Edwige is not a member of Human.
Introduction Knowledge Representation Semantic Web Reasoning Reasoning - Inference Inferences retrieves all the assertions which hold in all the possible models. TBox ABox Woman ≡ Female Human Woman(Alice) Man ≡ Male Human Man(Charlie) childOf ◦ relativeOf ⊆ relativeOf Alice childOf Charlie dom(ownerOf) Human Charlie relativeOf Bob Bob ownerOf Fido Inferred Statements
Introduction Knowledge Representation Semantic Web Reasoning Reasoning - Inference Inferences retrieves all the assertions which hold in all the possible models. TBox ABox Woman ≡ Female Human Woman(Alice) Man ≡ Male Human Man(Charlie) childOf ◦ relativeOf ⊆ relativeOf Alice childOf Charlie dom(ownerOf) Human Charlie relativeOf Bob Bob ownerOf Fido Inferred Statements Female(Alice) Human(Alice)
Introduction Knowledge Representation Semantic Web Reasoning Reasoning - Inference Inferences retrieves all the assertions which hold in all the possible models. TBox ABox Woman ≡ Female Human Woman(Alice) Man ≡ Male Human Man(Charlie) childOf ◦ relativeOf ⊆ relativeOf Alice childOf Charlie dom(ownerOf) Human Charlie relativeOf Bob Bob ownerOf Fido Inferred Statements Female(Alice) Human(Alice) Male(Charlie) Human(Charlie)
Introduction Knowledge Representation Semantic Web Reasoning Reasoning - Inference Inferences retrieves all the assertions which hold in all the possible models. TBox ABox Woman ≡ Female Human Woman(Alice) Man ≡ Male Human Man(Charlie) childOf ◦ relativeOf ⊆ relativeOf Alice childOf Charlie dom(ownerOf) Human Charlie relativeOf Bob Bob ownerOf Fido Inferred Statements Female(Alice) Human(Alice) Male(Charlie) Human(Charlie) Alice relativeOf Bob
Introduction Knowledge Representation Semantic Web Reasoning Reasoning - Inference Inferences retrieves all the assertions which hold in all the possible models. TBox ABox Woman ≡ Female Human Woman(Alice) Man ≡ Male Human Man(Charlie) childOf ◦ relativeOf ⊆ relativeOf Alice childOf Charlie dom(ownerOf) Human Charlie relativeOf Bob Bob ownerOf Fido Inferred Statements Female(Alice) Human(Alice) Male(Charlie) Human(Charlie) Alice relativeOf Bob Human(Bob)
Introduction Knowledge Representation Semantic Web Reasoning Thank You! (questions?)

More Related Content

PDF
An Approach to Automated Learning of Conceptual Graphs from Text
byFulvio Rotella
 
PPTX
Knowledge representation and reasoning
byMaryam Maleki
 
PDF
Ontological Conjunctive Query Answering over large, semi-structured knowledge...
bygraphdevroom
 
PPTX
Human Level Artificial Intelligence
byRahul Chaurasia
 
PPT
Halo Pcs Kcap2007 V2
byJose Manuel Gómez-Pérez
 
PDF
Knowledge Representation and Reasoning with Apache Stanbol
byAndrea Nuzzolese
 
PDF
Linked Census Data
byRinke Hoekstra
 
PPSX
Artificial intelligence01
byMemory Silver
 
An Approach to Automated Learning of Conceptual Graphs from Text
byFulvio Rotella
 
Knowledge representation and reasoning
byMaryam Maleki
 
Ontological Conjunctive Query Answering over large, semi-structured knowledge...
bygraphdevroom
 
Human Level Artificial Intelligence
byRahul Chaurasia
 
Halo Pcs Kcap2007 V2
byJose Manuel Gómez-Pérez
 
Knowledge Representation and Reasoning with Apache Stanbol
byAndrea Nuzzolese
 
Linked Census Data
byRinke Hoekstra
 
Artificial intelligence01
byMemory Silver
 

Viewers also liked

PPTX
Semantic Perspectives for Contemporary Question Answering Systems
byAndre Freitas
 
PPT
Artificial Intelligence
byu053675
 
PPTX
Knowledge representation in AI
byVishal Singh
 
PDF
Deep Learning - The Past, Present and Future of Artificial Intelligence
byLukas Masuch
 
PPTX
What is knowledge representation and reasoning ?
byAnant Soft Computing
 
PPT
First order logic
byRushdi Shams
 
PPT
Artificial intelligence and Neural Network
byAbdullah Saghir Ahmad
 
PPTX
Classical relations and fuzzy relations
byBaran Kaynak
 
PPT
Artificial Intelligence
byNeil Mathew
 
PPT
Robotics & Artificial Intelligence
byAnthony Caramele
 
PDF
Knowledge Representation on the Web
byRinke Hoekstra
 
PPTX
Artificial Intelligence Presentation
bylpaviglianiti
 
PPTX
Knowledge Representation essay outline
bymondesser
 
Semantic Perspectives for Contemporary Question Answering Systems
byAndre Freitas
 
Artificial Intelligence
byu053675
 
Knowledge representation in AI
byVishal Singh
 
Deep Learning - The Past, Present and Future of Artificial Intelligence
byLukas Masuch
 
What is knowledge representation and reasoning ?
byAnant Soft Computing
 
First order logic
byRushdi Shams
 
Artificial intelligence and Neural Network
byAbdullah Saghir Ahmad
 
Classical relations and fuzzy relations
byBaran Kaynak
 
Artificial Intelligence
byNeil Mathew
 
Robotics & Artificial Intelligence
byAnthony Caramele
 
Knowledge Representation on the Web
byRinke Hoekstra
 
Artificial Intelligence Presentation
bylpaviglianiti
 
Knowledge Representation essay outline
bymondesser
 

Similar to Adding Semantics to Ontologies

PDF
Ch 7 Knowledge Representation.pdf
byKrishnaMadala1
 
PPTX
"Why the Semantic Web will Never Work" (note the quotes)
byJames Hendler
 
PPTX
sOCIAL NETWORK ANALYSIS AND ONTOLOGIES A VIEW
bysyedanwarf
 
PDF
Ontology Engineering Synthesis Lectures on Data Semantics and Knowledge 1st ...
bybobelelmien
 
PDF
Ontology development
byStefano Bragaglia
 
PPT
Knowldge reprsentations
byTribhuvan University
 
PPT
Reasoning on the Semantic Web
byYannis Kalfoglou
 
PDF
Knowledge Representation In The Social Semantic Web Katrin Weller
byjuniamonekfv
 
PPT
Towards Linked Ontologies and Data on the Semantic Web
byJie Bao
 
PPT
Lri Owl And Ontologies 04 04
byRinke Hoekstra
 
PPT
Representing and Reasoning with Modular Ontologies
byJie Bao
 
PDF
Effective Semantics for Engineering NLP Systems
byAndre Freitas
 
PPTX
Semantic Modelling using Semantic Web Technology
byRinke Hoekstra
 
PPTX
BT02.pptx
byThAnhonc
 
PPT
Ontology modelling and the semantic web
byasgeirr
 
PDF
A category theoretic model of rdf ontology
byIJwest
 
PPTX
Jim Hendler's Presentation at SSSW 2011
bysssw2011
 
PDF
Artificial Intelligence of the Web through Domain Ontologies
byInternational Journal of Science and Research (IJSR)
 
PPT
Where Does It Break?
byFrank van Harmelen
 
PDF
A Contextualized Knowledge Repository for Open Data about Trentino
byPlanetData Network of Excellence
 
Ch 7 Knowledge Representation.pdf
byKrishnaMadala1
 
"Why the Semantic Web will Never Work" (note the quotes)
byJames Hendler
 
sOCIAL NETWORK ANALYSIS AND ONTOLOGIES A VIEW
bysyedanwarf
 
Ontology Engineering Synthesis Lectures on Data Semantics and Knowledge 1st ...
bybobelelmien
 
Ontology development
byStefano Bragaglia
 
Knowldge reprsentations
byTribhuvan University
 
Reasoning on the Semantic Web
byYannis Kalfoglou
 
Knowledge Representation In The Social Semantic Web Katrin Weller
byjuniamonekfv
 
Towards Linked Ontologies and Data on the Semantic Web
byJie Bao
 
Lri Owl And Ontologies 04 04
byRinke Hoekstra
 
Representing and Reasoning with Modular Ontologies
byJie Bao
 
Effective Semantics for Engineering NLP Systems
byAndre Freitas
 
Semantic Modelling using Semantic Web Technology
byRinke Hoekstra
 
BT02.pptx
byThAnhonc
 
Ontology modelling and the semantic web
byasgeirr
 
A category theoretic model of rdf ontology
byIJwest
 
Jim Hendler's Presentation at SSSW 2011
bysssw2011
 
Artificial Intelligence of the Web through Domain Ontologies
byInternational Journal of Science and Research (IJSR)
 
Where Does It Break?
byFrank van Harmelen
 
A Contextualized Knowledge Repository for Open Data about Trentino
byPlanetData Network of Excellence
 

More from Cristiano Longo

PDF
Semantic Web e Linked Open Data - Parte I
byCristiano Longo
 
PDF
Linked Open Data e Semantic Web: Fondamenti e Linguaggi di Interrogazione - P...
byCristiano Longo
 
PDF
Linked Open Data for Cultural Heritage
byCristiano Longo
 
PDF
Herbrand-satisfiability of a Quantified Set-theoretical Fragment (Cantone, Lo...
byCristiano Longo
 
PDF
Open Data di Comunità
byCristiano Longo
 
PDF
OpenDataTour: CO.P.E.
byCristiano Longo
 
PDF
Sulle Linee Guida per gli Open Data nei Comuni
byCristiano Longo
 
PDF
Open Data e Open Data Sicilia
byCristiano Longo
 
PDF
Introduzione ai Linked Open Data e al Web Semantico
byCristiano Longo
 
PDF
Attivismo Open Data a Catania: dal tour all'hacklab
byCristiano Longo
 
PDF
Beni Culturali Aperti
byCristiano Longo
 
Semantic Web e Linked Open Data - Parte I
byCristiano Longo
 
Linked Open Data e Semantic Web: Fondamenti e Linguaggi di Interrogazione - P...
byCristiano Longo
 
Linked Open Data for Cultural Heritage
byCristiano Longo
 
Herbrand-satisfiability of a Quantified Set-theoretical Fragment (Cantone, Lo...
byCristiano Longo
 
Open Data di Comunità
byCristiano Longo
 
OpenDataTour: CO.P.E.
byCristiano Longo
 
Sulle Linee Guida per gli Open Data nei Comuni
byCristiano Longo
 
Open Data e Open Data Sicilia
byCristiano Longo
 
Introduzione ai Linked Open Data e al Web Semantico
byCristiano Longo
 
Attivismo Open Data a Catania: dal tour all'hacklab
byCristiano Longo
 
Beni Culturali Aperti
byCristiano Longo
 

Recently uploaded

PDF
Deep-Behavioral Phenotyping in Systems Neuroscience for Functional Atlasing a...
byAna Luísa Pinho
 
PDF
Mechanical Properties of Fluids (Prashant Kirad).pdf
byarleenaulakh97
 
PPTX
PRE NATAL GROWTH OF MAXILLA in orthodontics.pptx
byharanip03
 
PDF
Presentacion Cap. 22_d078bd243e36ee08576f0f6412f24754.pdf
byXamaitaTrinidad
 
PDF
12th Bio NCERT Important Questions @irfanullah_ mehar.pdf
byWorld of Wisdom
 
PPTX
Ppt-about-Reproductive-Endocrine-and-Nervous-System.pptx
byeunicejayzenn
 
PDF
SS-Geologic Time Scale-EON, ERA,PERIOD,EPOCH
bySandraMaeSubaan1
 
PDF
Star Constollations and Quasars.pdf Files
bycastilloronelparro22
 
PDF
Cardiovascular Nanomedicines: A Review of Nanoparticle-Mediated Strategies fo...
bykarishmayjm
 
PPTX
Lecture 3_CellStructureFunction_2025.pptx
byAngelMaria66
 
PPTX
Polarity - Polar and non-polar, electronegativity and molecular geometry
byJovenAlvarado
 
PPTX
cellstructurefunction-190628175900..PPTX
byAubreyDilla
 
PPTX
Trusted Industrial Ammonia Supply – Contact Us
bymysoreammoniaseo
 
PPTX
genesilencing and gene engineering of technilogy
bymhossainkhan2022
 
PPT
What is Ecosystem Stability and its relevance.ppt
byWorrelThomas1
 
PPTX
Avascular necrosis of femoral head of femur.pptx
bynazsky86716
 
PPTX
ALLOSTERIC INHIBITION : ITS CHARACTERISTICS, STRUCTURE AND MECHANISMS
byaubrey02judd
 
PPTX
GRANULOCYTES: NEUTROPHILS, EOSINOPHIL AND BASOPHIL
byBIOSPHERE OF KNOWLEDGE
 
PPTX
Cell cycle part 2 (Mitosis, Meiosis, Differences, Nondisjuction and Aneuploid...
byRashmiMG2
 
PPTX
All-About-Missiles-----------------.pptx
byOmkarWandhekar
 
Deep-Behavioral Phenotyping in Systems Neuroscience for Functional Atlasing a...
byAna Luísa Pinho
 
Mechanical Properties of Fluids (Prashant Kirad).pdf
byarleenaulakh97
 
PRE NATAL GROWTH OF MAXILLA in orthodontics.pptx
byharanip03
 
Presentacion Cap. 22_d078bd243e36ee08576f0f6412f24754.pdf
byXamaitaTrinidad
 
12th Bio NCERT Important Questions @irfanullah_ mehar.pdf
byWorld of Wisdom
 
Ppt-about-Reproductive-Endocrine-and-Nervous-System.pptx
byeunicejayzenn
 
SS-Geologic Time Scale-EON, ERA,PERIOD,EPOCH
bySandraMaeSubaan1
 
Star Constollations and Quasars.pdf Files
bycastilloronelparro22
 
Cardiovascular Nanomedicines: A Review of Nanoparticle-Mediated Strategies fo...
bykarishmayjm
 
Lecture 3_CellStructureFunction_2025.pptx
byAngelMaria66
 
Polarity - Polar and non-polar, electronegativity and molecular geometry
byJovenAlvarado
 
cellstructurefunction-190628175900..PPTX
byAubreyDilla
 
Trusted Industrial Ammonia Supply – Contact Us
bymysoreammoniaseo
 
genesilencing and gene engineering of technilogy
bymhossainkhan2022
 
What is Ecosystem Stability and its relevance.ppt
byWorrelThomas1
 
Avascular necrosis of femoral head of femur.pptx
bynazsky86716
 
ALLOSTERIC INHIBITION : ITS CHARACTERISTICS, STRUCTURE AND MECHANISMS
byaubrey02judd
 
GRANULOCYTES: NEUTROPHILS, EOSINOPHIL AND BASOPHIL
byBIOSPHERE OF KNOWLEDGE
 
Cell cycle part 2 (Mitosis, Meiosis, Differences, Nondisjuction and Aneuploid...
byRashmiMG2
 
All-About-Missiles-----------------.pptx
byOmkarWandhekar
 

Adding Semantics to Ontologies

  • 1.
    Introduction Knowledge RepresentationSemantic Web Reasoning Adding Semantics to Ontologies Cristiano Longo Dipartimento di Matematica e Informatica, Universit`a di Catania, Italy mailto://longo@dmi.unict.it SOD2014
  • 2.
    Introduction Knowledge RepresentationSemantic Web Reasoning About This talk is about the word Semantic in the “Semantic Web.” It will provides some basic theoretical notions for a better understanding of Semantic Web technologies (in particular OWL).
  • 3.
    Introduction Knowledge RepresentationSemantic Web Reasoning Topics Some answers for the following questions will be provided: How can we represent knowledge? (ontologies) Which tools the Semantic Web framework offer to this end? (OWL) How representing knowledge with these tools can be useful? (reasoning)
  • 4.
    Introduction Knowledge RepresentationSemantic Web Reasoning Topics Some answers for the following questions will be provided: How can we represent knowledge? (ontologies) Which tools the Semantic Web framework offer to this end? (OWL) How representing knowledge with these tools can be useful? (reasoning)
  • 5.
    Introduction Knowledge RepresentationSemantic Web Reasoning Topics Some answers for the following questions will be provided: How can we represent knowledge? (ontologies) Which tools the Semantic Web framework offer to this end? (OWL) How representing knowledge with these tools can be useful? (reasoning)
  • 6.
    Introduction Knowledge RepresentationSemantic Web Reasoning Notice For the sake of readability and for historical reason, we will use notation and terminology from Descriptio Logics, which underpin Semantic Web languages (in particular OWL).
  • 7.
    Introduction Knowledge RepresentationSemantic Web Reasoning Representing Knowledge in Logic and Computer Science
  • 8.
    Introduction Knowledge RepresentationSemantic Web Reasoning Ontologies An ontology is a (partial) description of the world. Usually, it is a finite set of statements such as, for example, human beings are mortals, Alice is the Bob’s mother, Federico II was an emperor.
  • 9.
    Introduction Knowledge RepresentationSemantic Web Reasoning Basics A knowledge domain is described in terms of individuals, to indicate domain items (Alice, Bob, . . . ), concepts (aka classes), which denote sets of domain objects (Person, Male, . . . ), and roles (aka properties), which are relations on domain items (parentOf, partnerOf, . . . ).
  • 10.
    Introduction Knowledge RepresentationSemantic Web Reasoning Vocabulary and Assertions Each ontology is divided into two parts: the TBox(vocabulary), in which vocabulary terms for concepts (i.e. sets) and roles (i.e. relations) are defined, and the ABox, which contains statements (namely, assertions) about real world items. TBox Concepts: Male, Female,Human,Woman, Man. Roles: relativeOf, childOf, grandChildOf. ABox Woman(Alice), Man(Bob), Alice relativeOf Bob, Alice childOf Charlie.
  • 11.
    Introduction Knowledge RepresentationSemantic Web Reasoning Vocabulary and Assertions Each ontology is divided into two parts: the TBox(vocabulary), in which vocabulary terms for concepts (i.e. sets) and roles (i.e. relations) are defined, and the ABox, which contains statements (namely, assertions) about real world items. TBox Concepts: Male, Female,Human,Woman, Man. Roles: relativeOf, childOf, grandChildOf. ABox Woman(Alice), Man(Bob), Alice relativeOf Bob, Alice childOf Charlie.
  • 12.
    Introduction Knowledge RepresentationSemantic Web Reasoning Open World Assumption Facts not explicitly mentioned in the ontology are not assumed to be false, their truth value is just unknown. In general, no one has complete knowledge. TBox Concepts: Male, Female,Human,Woman, Man. Roles: relativeOf, childOf, grandChildOf. ABox Woman(Alice), Man(Bob), Alice relativeOf Bob, Alice childOf Charlie. What is the kinship relation between Alice and Bob? Charlie childOf Alice? Is Charlie a man? Is Charlie a human being? What about other persons in the world?
  • 13.
    Introduction Knowledge RepresentationSemantic Web Reasoning Open World Assumption Facts not explicitly mentioned in the ontology are not assumed to be false, their truth value is just unknown. In general, no one has complete knowledge. TBox Concepts: Male, Female,Human,Woman, Man. Roles: relativeOf, childOf, grandChildOf. ABox Woman(Alice), Man(Bob), Alice relativeOf Bob, Alice childOf Charlie. What is the kinship relation between Alice and Bob? Charlie childOf Alice? Is Charlie a man? Is Charlie a human being? What about other persons in the world?
  • 14.
    Introduction Knowledge RepresentationSemantic Web Reasoning Open World Assumption - Interpretations All the possible worlds must be taken into account. An interpretation associates sets, relations, and items of a given domain (i.e. Universe) ∆ to concepts and roles in the vocabulary. For example: ∆ := {Alice, Bob, Charlie, Dana, Edwige} Alice childOf Bob Human := {Alice, Bob, Charlie, Dana} Charlie relativeOf Bob Female := {Alice, Dana, Edwige} Male := {Bob, Charlie} Woman := {Alice, Dana} Man := {BobCharlie}
  • 15.
    Introduction Knowledge RepresentationSemantic Web Reasoning Open World Assumption - Interpretations All the possible worlds must be taken into account. An interpretation associates sets, relations, and items of a given domain (i.e. Universe) ∆ to concepts and roles in the vocabulary. For example: ∆ := {Alice, Bob, Charlie, Dana, Edwige} Alice childOf Bob Human := {Alice, Bob, Charlie, Dana} Charlie relativeOf Bob Female := {Alice, Dana, Edwige} Male := {Bob, Charlie} Woman := {Alice, Dana} Man := {BobCharlie}
  • 16.
    Introduction Knowledge RepresentationSemantic Web Reasoning Open World Assumption - Interpretations All the possible worlds must be taken into account. An interpretation associates sets, relations, and items of a given domain (i.e. Universe) ∆ to concepts and roles in the vocabulary. For example: ∆ := {Alice, Bob, Charlie, Dana, Edwige} Alice childOf Bob Human := {Alice, Bob, Charlie, Dana} Charlie relativeOf Bob Female := {Alice, Dana, Edwige} Male := {Bob, Charlie} Woman := {Alice, Dana} Man := {BobCharlie}
  • 17.
    Introduction Knowledge RepresentationSemantic Web Reasoning Open World Assumption - Models (1/2) Roughly speaking, an interpretation is a model for an ontology if it does not contradicts the ontology itself For example: ∆ := {Alice, Bob, Charlie, Dana, Edwige} Alice childOf Charlie Human := {Alice, Bob, Charlie, Dana} Charlie relativeOf Bob Female := {Alice, Dana, Edwige} Male := {Bob, Charlie} Woman := {Alice, Dana} Man := {BobCharlie} is a model for TBox Concepts: Male, Female,Human,Woman, Man. Roles: relativeOf, childOf, grandChildOf. ABox Woman(Alice), Man(Bob), Alice relativeOf Bob, Alice childOf Charlie.
  • 18.
    Introduction Knowledge RepresentationSemantic Web Reasoning Open World Assumption - Models (2/2) Wherease the following is not. ∆ := {Alice, Bob, Charlie, Dana, Edwige} Alice relativeOf Charlie Human := {Alice, Bob, Charlie, Dana} Charlie relativeOf Bob Female := {Alice, Dana, Edwige} Male := {Bob, Charlie} Woman := {Alice, Dana} Man := {BobCharlie} TBox Concepts: Male, Female,Human,Woman, Man. Roles: relativeOf, childOf, grandChildOf. ABox Woman(Alice), Man(Bob), Alice relativeOf Bob, Alice childOf Charlie.
  • 19.
    Introduction Knowledge RepresentationSemantic Web Reasoning Constraints How to to associate meanings to vocabulary terms: by means of constraints (placed in the TBox) expressed in a mathematical fashion involving concepts, roles, individuals. Example Human Mortal all persons are mortal; Woman ≡ Human Female women are female human beings; childOf ◦ childOf ⊆ grandChildOf the child of the child is the grandchild. In general, the syntax of a Knowledge Representation Language is characterized by the types of constraints it allows, mainly in term of operators (eg. , ◦, . . . ).
  • 20.
    Introduction Knowledge RepresentationSemantic Web Reasoning Constraints How to to associate meanings to vocabulary terms: by means of constraints (placed in the TBox) expressed in a mathematical fashion involving concepts, roles, individuals. Example Human Mortal all persons are mortal; Woman ≡ Human Female women are female human beings; childOf ◦ childOf ⊆ grandChildOf the child of the child is the grandchild. In general, the syntax of a Knowledge Representation Language is characterized by the types of constraints it allows, mainly in term of operators (eg. , ◦, . . . ).
  • 21.
    Introduction Knowledge RepresentationSemantic Web Reasoning Representing Knowledge the Semantic Web
  • 22.
    Introduction Knowledge RepresentationSemantic Web Reasoning Semantic Web Stack Semantic Web technologies are stratified. Figure: The Semantic Web stack
  • 23.
    Introduction Knowledge RepresentationSemantic Web Reasoning Representing Knowledge the Semantic Web Semantic Web technologies are stratified. Some of these are knowledge representation languages. Figure: The Semantic Web stack
  • 24.
    Introduction Knowledge RepresentationSemantic Web Reasoning OWL OWL is the concise name of the Web Ontology Language, currently at version 2. http://www.w3.org/TR/2012/REC-owl2-primer-20121211/ Three different profiles (fragments) have been defined for it (see http://www.w3.org/TR/2012/REC-owl2-profiles-20121211/): OWL-RL quite good expressive power; OWL-QL for large ABox; OWL-EL very efficient, also in presence of large TBox. Here we consider OWL-EL.
  • 25.
    Introduction Knowledge RepresentationSemantic Web Reasoning OWL OWL is the concise name of the Web Ontology Language, currently at version 2. http://www.w3.org/TR/2012/REC-owl2-primer-20121211/ Three different profiles (fragments) have been defined for it (see http://www.w3.org/TR/2012/REC-owl2-profiles-20121211/): OWL-RL quite good expressive power; OWL-QL for large ABox; OWL-EL very efficient, also in presence of large TBox. Here we consider OWL-EL.
  • 26.
    Introduction Knowledge RepresentationSemantic Web Reasoning OWL-EL and EL++ OWL-EL is underpinned by the description logic EL++. It has been devided in the biohealth domain (SNOMED-CT). Concept constructors of EL++ are: (every)thing; ⊥ nothing; {a} nominal, the set with only member a; ∃R.C existential restriction, all those items related with some element in C; C D conjunction, all the members of both C and D; concrete domains (e.g. age > 18). Such constructors can be used to form complex concepts, e.g. ∃childOf.{Fido} := {Edwige}, ∃childOf.(Male Human).
  • 27.
    Introduction Knowledge RepresentationSemantic Web Reasoning OWL-EL and EL++ OWL-EL is underpinned by the description logic EL++. It has been devided in the biohealth domain (SNOMED-CT). Concept constructors of EL++ are: (every)thing; ⊥ nothing; {a} nominal, the set with only member a; ∃R.C existential restriction, all those items related with some element in C; C D conjunction, all the members of both C and D; concrete domains (e.g. age > 18). Such constructors can be used to form complex concepts, e.g. ∃childOf.{Fido} := {Edwige}, ∃childOf.(Male Human).
  • 28.
    Introduction Knowledge RepresentationSemantic Web Reasoning OWL-EL and EL++ OWL-EL is underpinned by the description logic EL++. It has been devided in the biohealth domain (SNOMED-CT). Concept constructors of EL++ are: (every)thing; ⊥ nothing; {a} nominal, the set with only member a; ∃R.C existential restriction, all those items related with some element in C; C D conjunction, all the members of both C and D; concrete domains (e.g. age > 18). Such constructors can be used to form complex concepts, e.g. ∃childOf.{Fido} := {Edwige}, ∃childOf.(Male Human).
  • 29.
    Introduction Knowledge RepresentationSemantic Web Reasoning EL++ concepts - Thing Let us consider the following possible world (interpretation) ∆ := {Alice, Bob, Charlie, Dana, Edwige, Fido} Alice childOf Charlie Human := {Alice, Bob, Charlie, Dana} Alice childOf Dana Female := {Alice, Dana, Edwige} Edwige childOf Fido Male := {Bob, Charlie, Fido} Charlie relativeOf Bob Bob ownerOf Fido.
  • 30.
    Introduction Knowledge RepresentationSemantic Web Reasoning EL++ concepts - Thing Let us consider the following possible world ∆ := {Alice, Bob, Charlie, Dana, Edwige, Fido} Alice childOf Charlie Human := {Alice, Bob, Charlie, Dana} Alice childOf Dana Female := {Alice, Dana, Edwige} Edwige childOf Fido Male := {Bob, Charlie, Fido} Charlie relativeOf Bob Bob ownerOf Fido. := {Alice, Bob, Charlie, Dana, Edwige, Fido}
  • 31.
    Introduction Knowledge RepresentationSemantic Web Reasoning EL++ concepts - Nothing Let us consider the following possible world ∆ := {Alice, Bob, Charlie, Dana, Edwige, Fido} Alice childOf Charlie Human := {Alice, Bob, Charlie, Dana} Alice childOf Dana Female := {Alice, Dana, Edwige} Edwige childOf Fido Male := {Bob, Charlie, Fido} Charlie relativeOf Bob Bob ownerOf Fido. ⊥ := ∅
  • 32.
    Introduction Knowledge RepresentationSemantic Web Reasoning EL++ concepts - Nominal Let us consider the following possible world ∆ := {Alice, Bob, Charlie, Dana, Edwige, Fido} Alice childOf Charlie Human := {Alice, Bob, Charlie, Dana} Alice childOf Dana Female := {Alice, Dana, Edwige} Edwige childOf Fido Male := {Bob, Charlie, Fido} Charlie relativeOf Bob Bob ownerOf Fido. {Alice} := {Alice}
  • 33.
    Introduction Knowledge RepresentationSemantic Web Reasoning EL++ concepts - existential restriction Let us consider the following possible world ∆ := {Alice, Bob, Charlie, Dana, Edwige, Fido} Alice childOf Charlie Human := {Alice, Bob, Charlie, Dana} Alice childOf Dana Female := {Alice, Dana, Edwige} Edwige childOf Fido Male := {Bob, Charlie, Fido} Charlie relativeOf Bob Bob ownerOf Fido. ∃ownerOf.Male := {Bob}
  • 34.
    Introduction Knowledge RepresentationSemantic Web Reasoning EL++ concepts - conjunction (intersection) Let us consider the following possible world ∆ := {Alice, Bob, Charlie, Dana, Edwige, Fido} Alice childOf Charlie Human := {Alice, Bob, Charlie, Dana} Alice childOf Dana Female := {Alice, Dana, Edwige} Edwige childOf Fido Male := {Bob, Charlie, Fido} Charlie relativeOf Bob Bob ownerOf Fido. Female Human := {Alice, Dana}
  • 35.
    Introduction Knowledge RepresentationSemantic Web Reasoning EL++ concepts - complex concepts Let us consider the following possible world ∆ := {Alice, Bob, Charlie, Dana, Edwige, Fido} Alice childOf Charlie Human := {Alice, Bob, Charlie, Dana} Alice childOf Dana Female := {Alice, Dana, Edwige} Edwige childOf Fido Male := {Bob, Charlie, Fido} Charlie relativeOf Bob Bob ownerOf Fido. ∃childOf.{Fido} := {Edwige}
  • 36.
    Introduction Knowledge RepresentationSemantic Web Reasoning EL++ constraints Constraints allowed in EL++ TBox are of the types: C D every member of C is a member of D as well; C ≡ D the sets C and D coincide; R1 ◦ . . . ◦ Rn S the composition of R1, . . . , Rn is a subrelation of S; dom(R) C if x is related to y by R, then x must be a member of C; range(R) C if x is related to y by R, then y must be a member of C.
  • 37.
    Introduction Knowledge RepresentationSemantic Web Reasoning EL++ constraints - subsumption The following is a model for Man Human ∆ := {Alice, Bob, Charlie, Dana, Edwige, Fido} Alice childOf Charlie Human := {Alice, Bob, Charlie, Dana} Alice childOf Dana Female := {Alice, Dana, Edwige} Edwige childOf Fido Male := {Bob, Charlie, Fido} Charlie relativeOf Bob Man := {Bob, Charlie} Bob ownerOf Fido.
  • 38.
    Introduction Knowledge RepresentationSemantic Web Reasoning EL++ constraints - equivalence The same is a model for Man ≡ Human Male ∆ := {Alice, Bob, Charlie, Dana, Edwige, Fido} Alice childOf Charlie Human := {Alice, Bob, Charlie, Dana} Alice childOf Dana Female := {Alice, Dana, Edwige} Edwige childOf Fido Male := {Bob, Charlie, Fido} Charlie relativeOf Bob Man := {Bob, Charlie} Bob ownerOf Fido.
  • 39.
    Introduction Knowledge RepresentationSemantic Web Reasoning EL++ constraints - composition (1/2) Let us consider childOf ◦ relativeOf ⊆ relativeOf the child of a relative is a relative as well. The following is not a model for this constraint (Alice should be relative of Charlie): ∆ := {Alice, Bob, Charlie, Dana, Edwige, Fido} Alice childOf Charlie Human := {Alice, Bob, Charlie, Dana} Alice childOf Dana Female := {Alice, Dana, Edwige} Edwige childOf Fido Male := {Bob, Charlie, Fido} Charlie relativeOf Bob Man := {Bob, Charlie} Bob ownerOf Fido.
  • 40.
    Introduction Knowledge RepresentationSemantic Web Reasoning EL++ constraints - composition (2/2) A model for childOf ◦ relativeOf ⊆ relativeOf is: The following is not a model for this constraint (Alice should be relative of Bob): ∆ := {Alice, Bob, Charlie, Dana, Edwige, Fido} Alice childOf Charlie Human := {Alice, Bob, Charlie, Dana} Alice childOf Dana Female := {Alice, Dana, Edwige} Edwige childOf Fido Male := {Bob, Charlie, Fido} Charlie relativeOf Bob Man := {Bob, Charlie} Bob ownerOf Fido Alice relativeOf Bob.
  • 41.
    Introduction Knowledge RepresentationSemantic Web Reasoning EL++ constraints - domain It is a model for dom(ownerOf) Human all owners are humans. ∆ := {Alice, Bob, Charlie, Dana, Edwige, Fido} Alice childOf Charlie Human := {Alice, Bob, Charlie, Dana} Alice childOf Dana Female := {Alice, Dana, Edwige} Edwige childOf Fido Male := {Bob, Charlie, Fido} Charlie relativeOf Bob Man := {Bob, Charlie} Bob ownerOf Fido.
  • 42.
    Introduction Knowledge RepresentationSemantic Web Reasoning EL++ constraints - range But this is not a model for range(ownerOf) Human all owned are humans. ∆ := {Alice, Bob, Charlie, Dana, Edwige, Fido} Alice childOf Charlie Human := {Alice, Bob, Charlie, Dana} Alice childOf Dana Female := {Alice, Dana, Edwige} Edwige childOf Fido Male := {Bob, Charlie, Fido} Charlie relativeOf Bob Man := {Bob, Charlie} Bob ownerOf Fido.
  • 43.
    Introduction Knowledge RepresentationSemantic Web Reasoning Using Knowledge encoded in EL++
  • 44.
    Introduction Knowledge RepresentationSemantic Web Reasoning Reasoning Defining a formal semantics enables some reasoning task to be performed automatically. Here we will see consistency checking, to check the absence of logical errors, inferencing, to extract hidden knowledge.
  • 45.
    Introduction Knowledge RepresentationSemantic Web Reasoning Reasoning - Consistency An ontology is consistent if a possible world which matches it exists. Let us consider the following ontology: TBox ABox Woman ≡ Female Human Woman(Alice) Man ≡ Male Human Man(Charlie) childOf ◦ relativeOf ⊆ relativeOf Alice childOf Charlie dom(ownerOf) Human Charlie relativeOf Bob Bob ownerOf Fido It is consistent (see before for a model).
  • 46.
    Introduction Knowledge RepresentationSemantic Web Reasoning Reasoning - Consistency - example 2 The following one is not consistent. TBox ABox Woman ≡ Female Human Woman(Alice) Man ≡ Male Human Man(Charlie) childOf ◦ relativeOf ⊆ relativeOf Alice childOf Charlie dom(ownerOf) Human Charlie relativeOf Bob Male Female ≡ ⊥ Bob ownerOf Fido Female(Bob) Bob must be Male, as it is a Man, all men are Male and Male and Female are disjoint.
  • 47.
    Introduction Knowledge RepresentationSemantic Web Reasoning Reasoning - Consistency - example 3 The following one is not consistent. TBox ABox Woman ≡ Female Human Woman(Alice) Man ≡ Male Human Man(Charlie) childOf ◦ relativeOf ⊆ relativeOf Alice childOf Charlie dom(ownerOf) Human Charlie relativeOf Bob Human Edwige ≡ ⊥ Bob ownerOf Fido Edwige ownerOf Fido Edwige can’t be the owner of Fido because Edwige is not a member of Human.
  • 48.
    Introduction Knowledge RepresentationSemantic Web Reasoning Reasoning - Inference Inferences retrieves all the assertions which hold in all the possible models. TBox ABox Woman ≡ Female Human Woman(Alice) Man ≡ Male Human Man(Charlie) childOf ◦ relativeOf ⊆ relativeOf Alice childOf Charlie dom(ownerOf) Human Charlie relativeOf Bob Bob ownerOf Fido Inferred Statements
  • 49.
    Introduction Knowledge RepresentationSemantic Web Reasoning Reasoning - Inference Inferences retrieves all the assertions which hold in all the possible models. TBox ABox Woman ≡ Female Human Woman(Alice) Man ≡ Male Human Man(Charlie) childOf ◦ relativeOf ⊆ relativeOf Alice childOf Charlie dom(ownerOf) Human Charlie relativeOf Bob Bob ownerOf Fido Inferred Statements Female(Alice) Human(Alice)
  • 50.
    Introduction Knowledge RepresentationSemantic Web Reasoning Reasoning - Inference Inferences retrieves all the assertions which hold in all the possible models. TBox ABox Woman ≡ Female Human Woman(Alice) Man ≡ Male Human Man(Charlie) childOf ◦ relativeOf ⊆ relativeOf Alice childOf Charlie dom(ownerOf) Human Charlie relativeOf Bob Bob ownerOf Fido Inferred Statements Female(Alice) Human(Alice) Male(Charlie) Human(Charlie)
  • 51.
    Introduction Knowledge RepresentationSemantic Web Reasoning Reasoning - Inference Inferences retrieves all the assertions which hold in all the possible models. TBox ABox Woman ≡ Female Human Woman(Alice) Man ≡ Male Human Man(Charlie) childOf ◦ relativeOf ⊆ relativeOf Alice childOf Charlie dom(ownerOf) Human Charlie relativeOf Bob Bob ownerOf Fido Inferred Statements Female(Alice) Human(Alice) Male(Charlie) Human(Charlie) Alice relativeOf Bob
  • 52.
    Introduction Knowledge RepresentationSemantic Web Reasoning Reasoning - Inference Inferences retrieves all the assertions which hold in all the possible models. TBox ABox Woman ≡ Female Human Woman(Alice) Man ≡ Male Human Man(Charlie) childOf ◦ relativeOf ⊆ relativeOf Alice childOf Charlie dom(ownerOf) Human Charlie relativeOf Bob Bob ownerOf Fido Inferred Statements Female(Alice) Human(Alice) Male(Charlie) Human(Charlie) Alice relativeOf Bob Human(Bob)
  • 53.
    Introduction Knowledge RepresentationSemantic Web Reasoning Thank You! (questions?)