Il documento tratta delle ontologie, delle interrogazioni e dei vocabolari nel contesto del web semantico e dei linked open data, evidenziando le difficoltà nell'interpretazione delle informazioni attualmente disponibili sul web. Descrive come le tecnologie promosse dal W3C affrontano le limitazioni del web tradizionale attraverso linguaggi di rappresentazione e query complesse labilitando interrogazioni tra database diversi. Inoltre, introduce la nozione di ontologie e di reasoning come strumenti per estrarre conoscenza implicita, insieme a esempi pratici di interrogazioni su dati semantici.

1. Introduzione Ontologie Interrogazioni Vocabolari
Linked Open Data e Semantic Web:
Fondamenti e Linguaggi di Interrogazione
Parte Prima
Cristiano Longo
longo@dmi.unict.it
Universita di Catania, 2014-2015

2. Introduzione Ontologie Interrogazioni Vocabolari
Argomenti
Questa presentazione trattera i seguenti argomenti:
Motivazioni del Web Semantico
De

3. nizione formale di Ontologie
Interrogazioni sulle Ontologie
Vocabolari

4. Introduzione Ontologie Interrogazioni Vocabolari
World Wide Web Consortium
Le tecnologie del Web Semantico rispondono ad un insieme di standard e protocolli
promossi e mantenuti dal World Wide Web Consortium (in breve W3C, vedi
http://www.w3.org).
Il W3C e un consorzio di standardizzazione per il Web che conta 403 membri tra
aziende e organizzazioni governative: CNR, Microsoft Corporation, Apple Inc., Intel
Corporation, Facebook, Google Inc., . . .
Altri standard sviluppati in seno al W3C sono: URL, HTTP, XML, HTML, CSS,
SOAP, WSDL, Javascript.

5. Introduzione Ontologie Interrogazioni Vocabolari
Limiti del World Wide Web (1/4)
The Web was designed as an information space, with the goal that it should
be useful not only for human-human communication, but also that machines
would be able to participate and help. One of the major obstacles to this has
been the fact that most information on the Web is designed for human
consumption, and even if it was derived from a database with well de

6. ned
meanings (in at least some terms) for its columns, that the structure of the
data is not evident to a robot browsing the web.
Semantic Web Roadmap, Tim Berners-Lee, 1998.

7. Introduzione Ontologie Interrogazioni Vocabolari
Limiti del World Wide Web (2/4)
Alcuni problemi nell'interpretazione di testi derivano da:
Lingue Dierenti e.g. Parigi e Paris possono indicare la stessa citta.
Omonimie e.g. esistono svariate citta chiamate Paris nel mondo (Arkansas,
Idaho, Illinois, Kentucky, Maine, Michigan, Missouri, New York, . . . );

8. Introduzione Ontologie Interrogazioni Vocabolari
Limiti del World Wide Web (3/4)
La situazione si complica in presenza di contenuti multimediali.

9. Introduzione Ontologie Interrogazioni Vocabolari
Limiti del World Wide Web (4/4)
Come conseguenza, spesso e impossibile eseguire su web ricerce complesse ottenendo
risultati accurati. Ad esempio, cercando sul web Federico II places non si ottengono
risultati in prima pagina su Federico II, ma solo sull'omonima universita:
1 Universita degli Studi di Napoli Federico II | OPEN Places
2 AOU - Policlinico Federico II - Napoli, Italy - Hospital | Facebook
3 Federico II Ingegneria Via Claudio - College and University | Facebook
4 MARIA CATERINA FONTE - www.docenti.unina.it

10. Introduzione Ontologie Interrogazioni Vocabolari
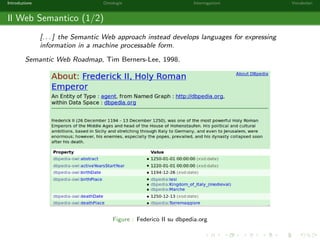
Il Web Semantico (1/2)
[. . . ] the Semantic Web approach instead develops languages for expressing
information in a machine processable form.
Semantic Web Roadmap, Tim Berners-Lee, 1998.
Figure : Federico II su dbpedia.org

11. Introduzione Ontologie Interrogazioni Vocabolari
Il Web Semantico (1/2)
I linguaggi di rappresentazione usati nel Web semantico hanno una sintassi rigorosa e
sono dotati di una semantica formale.
Questo rende possibile eettuare interrogazioni complesse sui dataset, ottenendo dei
risultati precisi anche se a volte parziali:
Q = Luoghi di nascita di Federico II e dei suoi parenti stretti .

12. Introduzione Ontologie Interrogazioni Vocabolari
Linked Open Data Cloud (1/2)
The Semantic Web is a web of data, in some ways like a global database.
Semantic Web Roadmap, Tim Berners-Lee, 1998.
Figure : Linked Open Data Cloud

13. Introduzione Ontologie Interrogazioni Vocabolari
Linked Open Data Cloud (2/2)
Nel Linked Open Data Cloud sono presenti 365 dataset (fonte
http://stats.lod2.eu/).
Alcuni dataset:
DBPedia (dbpedia.org) corrispondente a wikipedia.org;
Linked Movie Database (http://linkedmdb.org/) controparte sul Web
Semantico di Internet Movie Database (http://www.imdb.com/);
Linked GeoData (http://linkedgeodata.org) contiene i dati di OpenStreetMap
(http://www.openstreetmap.org/);
AGROVOC (http://aims.fao.org/agrovoc) e il dataset della FAO
(http://fao.org);
Europeana (http://pro.europeana.eu/linked-open-data) contiene dati su
beni culturali e tradizioni Europee.

14. Introduzione Ontologie Interrogazioni Vocabolari
Linked Data (1/2)
I dataset nel Web Semantico possono essere collegati tra loro. Ad esempio, una stessa
risorsa puo essere descritta sotto diversi aspetti in dataset dierenti.
Ad esempio, la citta di Catania e presente:
come pubblica amministrazione nel dataset del sistema pubblico di connettivita e
cooperazione http://spcdata.digitpa.gov.it/;
come divisione amministrativa nel dataset http://www.geonames.org;
come area territoriale nel dataset dell'ISTAT
http://linkedstat.spaziodati.eu/.

15. Introduzione Ontologie Interrogazioni Vocabolari
Linked Data (2/2)
E
possibile eettuare interrogazioni che coinvolgano diversi dataset (anche
eterogenei).
Ad esempio, la seguente query puo essere eseguita interrogando un data set
contenente dati storici ed uno sulle strutture ricettive:
Q = Strutture ricettive nei luoghi di nascita di Federico II e dei suoi parenti stretti.

16. Introduzione Ontologie Interrogazioni Vocabolari
Ontologie
I dataset del Web Semantico vengono spesso de

17. niti ontologie.
Una ontologia e una descrizione parziale del mondo:
descrive una porzione del mondo, spesso e limitata ad un'unico dominio di
conoscenza;
non si assume che i fatti non esplicitamente presenti nell'ontologia siano falsi
(Open World Assumption).
Essa e costituita da un insieme

18. nito di aermazioni. Ad esempio:
Tutti gli esseri umani sono mortali;
Socrate e mortale;
Alice e la madre di Roberto.

19. Introduzione Ontologie Interrogazioni Vocabolari
Ontologie - Aermazioni
Le aermazioni contenute in una ontologia sono di tre tipi:
Constraints: impongono dei vincoli semantici sul dominio di conoscenza che si va a
rappresentare. La notazione richiama quella insiemistica;
HumanBeing v Mortal
Property Assertions: impongono una relazione tra due elementi del dominio;
Alice motherOf Bob
Class Assertions: indicano l'appartenenza di un elemento ad un insieme.
HumanBeing(Socrate)

20. Introduzione Ontologie Interrogazioni Vocabolari
Ontologie - Reasoning
Con il termine reasoning si intende l'attivita di estrazione di conoscenza implicita in
una ontologia.
HumanBeing v Mortal;
HumanBeing(Socrate)
=) Mortal(Socrate)
Le attivita di reasoning sono rese possibili dalle semantiche formali associate ai
linguaggi di rappresentazione utilizzati.

21. Introduzione Ontologie Interrogazioni Vocabolari
Ontologie - De

22. nizione
Siano NC , NP, NI tre insiemi in

23. niti, numerabili e a due a due disgiunti di nomi di
classe, proprieta e individuo, rispettivamente.
Una ontologia e un insieme

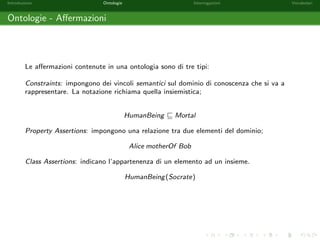
24. nito di asserzioni dei seguenti tipi:
Sintassi Semantica
Constraints C v D (8x)(x 2 C ! x 2 D)
R v S (8x; y)([x; y] 2 R ! [x; y] 2 S)
dom(R) v C (8x; y)([x; y] 2 R ! x 2 C)
range(R) v C (8x; y)([x; y] 2 R ! y 2 C)
Class Assertions C(a) a 2 C
Property Assertions a P b (equivalente P(a; b)) [a; b] 2 P
dove C;D 2 NC , R; S 2 NP e a; b 2 NI .

25. Introduzione Ontologie Interrogazioni Vocabolari
Ontologie - Esempio
Riportiamo un esempio di ontologia. Siano HumanBeing;Mortal 2 NC ,
teacherOf 2 NP, Socrate; Platone 2 NI .
O = fHumanBeing v Mortal;
range(teacherOf ) v HumanBeing;
HumanBeing(Socrate);
Socrate teacherOf Platoneg

26. Introduzione Ontologie Interrogazioni Vocabolari
Ontologie - Esempio
Riportiamo un esempio di ontologia. Siano HumanBeing;Mortal 2 NC ,
teacherOf 2 NP, Socrate; Platone 2 NI .
Mediante reasoning e possibile esplicitare ulteriori aermazioni.
O = fHumanBeing v Mortal; O0 = fMortal(Socrate);
range(teacherOf ) v HumanBeing; =)
HumanBeing(Socrate); g
Socrate teacherOf Platoneg

27. Introduzione Ontologie Interrogazioni Vocabolari
Ontologie - Esempio
Riportiamo un esempio di ontologia. Siano HumanBeing;Mortal 2 NC ,
teacherOf 2 NP, Socrate; Platone 2 NI .
Mediante reasoning e possibile esplicitare ulteriori aermazioni.
O = fHumanBeing v Mortal; O0 = fMortal(Socrate);
range(teacherOf) v HumanBeing; =) HumanBeing(Platone);
HumanBeing(Socrate); g
Socrate teacherOf Platoneg

28. Introduzione Ontologie Interrogazioni Vocabolari
Ontologie - Esempio
Riportiamo un esempio di ontologia. Siano HumanBeing;Mortal 2 NC ,
teacherOf 2 NP, Socrate; Platone 2 NI .
Mediante reasoning e possibile esplicitare ulteriori aermazioni.
O = fHumanBeing v Mortal O0 = fMortal(Socrate);
range(teacherOf ) v HumanBeing; =) HumanBeing(Platone)
HumanBeing(Socrate); Mortal(Platone)g
Socrate teacherOf Platoneg

29. Introduzione Ontologie Interrogazioni Vocabolari
Interrogazioni
Il metodo piu immediato per ottenere informazioni da una ontologia e il Conjunctive
Query Answering. Consideriamo ad esempio la seguente ontologia:
O = fFemale(Elise); Female(Alice); Male(Bob);
Male(Charlie); Male(Daniel);
Alice childOf Elise; Charlie childOf Elise;
Daniel childOf Alice; Daniel childOf Bob;
Francis childOf Charlieg
Alcune interrogazioni che e possibile eettuare con il conjunctive query answering
sono:
Trova tutti gli individui maschi.
Chi sono gli individui con almeno un

30. glio maschio?
Chi sono i

31. gli di Alice?
Chi sono gli individui con almeno un

32. glio maschio ed una femmina?
Chi sono gli individui maschi con almeno un

33. glio maschio?

34. Introduzione Ontologie Interrogazioni Vocabolari
Formule Atomiche
Per de

35. nire in maniera rigorosa le query congiuntive e necessario de

36. nire
preliminarmente l'insieme delle formule atomiche.
Sia V = fx; y; z; :::g l'insieme in

37. nito, numerabile e disgiunto da NC , NP e NI delle
variabili. Le formule atomiche sono espressioni dei due seguenti tipi:
C(x); P(x; y)
con x; y 2 NI [ V, P 2 NC e P 2 NP.
Esempi di formule atomiche sono:
HumanBeing(x),
x childOf Alice,
Bob childOf x,
x childOf y,
Mortal(Socrate),
Alice childOf Elise
con HumanBeing;Mortal 2 NC , childOf 2 NP, Alice; Bob; Elise 2 NI e x; y 2 V.

38. Introduzione Ontologie Interrogazioni Vocabolari
Formule Atomiche Chiuse
Una formula atomica nella quale non compaiano variabili si dice chiusa.
Negli esempi che seguono sono evidenziate le formule atomiche chiuse:
HumanBeing(x),
x childOf Alice,
Bob childOf x,
x childOf y,
Mortal(Socrate),
Alice childOf Elise
con HumanBeing;Mortal 2 NC , childOf 2 NP, Alice; Bob; Elise 2 NI e x; y 2 V.

39. Introduzione Ontologie Interrogazioni Vocabolari
Formule Atomiche Chiuse
Una formula atomica nella quale non compaiano variabili si dice chiusa.
Negli esempi che seguono sono evidenziate le formule atomiche chiuse:
HumanBeing(x),
x childOf Alice,
Bob childOf x,
x childOf y,
Mortal(Socrate),
Alice childOf Elise
con HumanBeing;Mortal 2 NC , childOf 2 NP, Alice; Bob; Elise 2 NI e x; y 2 V.
Le asserzioni presenti nelle ontologie sono formule atomiche chiuse.

40. Introduzione Ontologie Interrogazioni Vocabolari
Query Congiuntive
Una query congiuntiva e una congiunzione

41. nita di formule atomiche T1 ^ : : : ^ Tn.
Alcuni esempi di query congiuntive:
Trova tutti gli individui maschi.
Male(x)
Chi sono gli individui con almeno un

42. glio maschio?
y childOf x ^ Male(y)
Chi sono i

43. gli di Alice?
x childOf Alice
con x; y 2 V, Male; Female 2 NC , childOf 2 NP e Alice 2 NI .

44. Introduzione Ontologie Interrogazioni Vocabolari
Sostituzioni (1/2)
Per de

45. nire le soluzioni (risposte) delle query congiuntive introduciamo la nozione di
sostituzione.
Una sostituzione = [x1 ! a1; : : : ; xn ! an] (x1; : : : ; xn 2 V, a1; : : : ; an 2 NI ) e una
mappa

46. nita che associa nomi di individui a variabili.
Sia T una formula atomica e = [x1 ! a1; : : : ; xn ! an] una sostituzione.
L'applicazione T di a T e la formula atomica che si ottiene sostituendo in T ad
ogni occorrenza della variabile xi il corrispondente nome di individuo ai , per ogni
1 i n.
Alcuni esempi:
Male(x)[x ! Bob] = Male(Bob)
Male(x)[y ! Bob] =
(x childOf y)[x ! Alice] =
(x childOf y)[x ! Alice; y ! Elise] =
con x; y 2 V, Male 2 NC , childOf 2 NP e Alice; Bob; Elise 2 NI .

47. Introduzione Ontologie Interrogazioni Vocabolari
Sostituzioni (1/2)
Per de

48. nire le soluzioni (risposte) delle query congiuntive introduciamo la nozione di
sostituzione.
Una sostituzione = [x1 ! a1; : : : ; xn ! an] (x1; : : : ; xn 2 V, a1; : : : ; an 2 NI ) e una
mappa

49. nita che associa nomi di individui a variabili.
Sia T una formula atomica e = [x1 ! a1; : : : ; xn ! an] una sostituzione.
L'applicazione T di a T e la formula atomica che si ottiene sostituendo in T ad
ogni occorrenza della variabile xi il corrispondente nome di individuo ai , per ogni
1 i n.
Alcuni esempi:
Male(x)[x ! Bob] = Male(Bob)
Male(x)[y ! Bob] = Male(x)
(x childOf y)[x ! Alice] =
(x childOf y)[x ! Alice; y ! Elise] =
con x; y 2 V, Male 2 NC , childOf 2 NP e Alice; Bob; Elise 2 NI .

50. Introduzione Ontologie Interrogazioni Vocabolari
Sostituzioni (1/2)
Per de

51. nire le soluzioni (risposte) delle query congiuntive introduciamo la nozione di
sostituzione.
Una sostituzione = [x1 ! a1; : : : ; xn ! an] (x1; : : : ; xn 2 V, a1; : : : ; an 2 NI ) e una
mappa

52. nita che associa nomi di individui a variabili.
Sia T una formula atomica e = [x1 ! a1; : : : ; xn ! an] una sostituzione.
L'applicazione T di a T e la formula atomica che si ottiene sostituendo in T ad
ogni occorrenza della variabile xi il corrispondente nome di individuo ai , per ogni
1 i n.
Alcuni esempi:
Male(x)[x ! Bob] = Male(Bob)
Male(x)[y ! Bob] = Male(x)
(x childOf y)[x ! Alice] = Alice childOf y
(x childOf y)[x ! Alice; y ! Elise] =
con x; y 2 V, Male 2 NC , childOf 2 NP e Alice; Bob; Elise 2 NI .

53. Introduzione Ontologie Interrogazioni Vocabolari
Sostituzioni (1/2)
Per de

54. nire le soluzioni (risposte) delle query congiuntive introduciamo la nozione di
sostituzione.
Una sostituzione = [x1 ! a1; : : : ; xn ! an] (x1; : : : ; xn 2 V, a1; : : : ; an 2 NI ) e una
mappa

55. nita che associa nomi di individui a variabili.
Sia T una formula atomica e = [x1 ! a1; : : : ; xn ! an] una sostituzione.
L'applicazione T di a T e la formula atomica che si ottiene sostituendo in T ad
ogni occorrenza della variabile xi il corrispondente nome di individuo ai , per ogni
1 i n.
Alcuni esempi:
Male(x)[x ! Bob] = Male(Bob)
Male(x)[y ! Bob] = Male(x)
(x childOf y)[x ! Alice] = Alice childOf y
(x childOf y)[x ! Alice; y ! Elise] = Alice childOf Elise
con x; y 2 V, Male 2 NC , childOf 2 NP e Alice; Bob; Elise 2 NI .

56. Introduzione Ontologie Interrogazioni Vocabolari
Sostituzioni (2/2)
L'applicazione di sostituzioni a query congiuntive si de

57. nisce come segue.
Sia = [x1 ! a1; : : : ; xn ! an] una sostituzione e siano T1; : : : ;Tm formule atomiche.
Allora
(T1 ^ : : : ^ Tm) =Def T1 ^ : : : ^ Tm:
Alcuni esempi:
(y childOf x ^ Male(y))[x ! Alice] =Def
(y childOf x ^ Male(y))[x ! Alice; z ! Bob] =Def
(y childOf x ^ Male(y))[x ! Alice; y ! Bob] =Def

58. Introduzione Ontologie Interrogazioni Vocabolari
Sostituzioni (2/2)
L'applicazione di sostituzioni a query congiuntive si de

59. nisce come segue.
Sia = [x1 ! a1; : : : ; xn ! an] una sostituzione e siano T1; : : : ;Tm formule atomiche.
Allora
(T1 ^ : : : ^ Tm) =Def T1 ^ : : : ^ Tm:
Alcuni esempi:
(y childOf x ^ Male(y))[x ! Alice] =Def y childOf Alice ^ Male(y)
(y childOf x ^ Male(y))[x ! Alice; z ! Bob] =Def
(y childOf x ^ Male(y))[x ! Alice; y ! Bob] =Def

60. Introduzione Ontologie Interrogazioni Vocabolari
Sostituzioni (2/2)
L'applicazione di sostituzioni a query congiuntive si de

61. nisce come segue.
Sia = [x1 ! a1; : : : ; xn ! an] una sostituzione e siano T1; : : : ;Tm formule atomiche.
Allora
(T1 ^ : : : ^ Tm) =Def T1 ^ : : : ^ Tm:
Alcuni esempi:
(y childOf x ^ Male(y))[x ! Alice] =Def y childOf Alice ^ Male(y)
(y childOf x ^ Male(y))[x ! Alice; z ! Bob] =Def y childOf Alice ^ Male(y)
(y childOf x ^ Male(y))[x ! Alice; y ! Bob] =Def

62. Introduzione Ontologie Interrogazioni Vocabolari
Sostituzioni (2/2)
L'applicazione di sostituzioni a query congiuntive si de

63. nisce come segue.
Sia = [x1 ! a1; : : : ; xn ! an] una sostituzione e siano T1; : : : ;Tm formule atomiche.
Allora
(T1 ^ : : : ^ Tm) =Def T1 ^ : : : ^ Tm:
Alcuni esempi:
(y childOf x ^ Male(y))[x ! Alice] =Def y childOf Alice ^ Male(y)
(y childOf x ^ Male(y))[x ! Alice; z ! Bob] =Def y childOf Alice ^ Male(y)
(y childOf x ^ Male(y))[x ! Alice; y ! Bob] =Def Bob childOf Alice ^ Male(Bob)

64. Introduzione Ontologie Interrogazioni Vocabolari
Soluzioni per una Query
Siano = [x1 ! a1; : : : ; xn ! an] una sostituzione, Q = T1 ^ : : : ^ Tm una query
congiuntiva e O una ontologia.
e detta essere una soluzione per Q rispetto ad O se e solo se T1; : : : ;T2
compaiono in O.
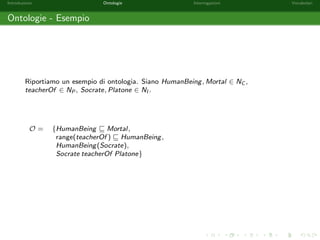
Consideriamo l'ontologia O e la query Q de

65. nite come segue:
O = fFemale(Elise); Female(Alice); Male(Bob);
Male(Charlie); Male(Daniel);
Alice childOf Elise; Charlie childOf Elise;
Daniel childOf Alice; Daniel childOf Bob;
Francis childOf Charlieg
Q = y childOf x ^ Male(y):
Sia 1 = [x ! Alice; y ! Daniel]. 1 e una soluzione per Q rispetto ad O?

66. Introduzione Ontologie Interrogazioni Vocabolari
Soluzioni per una Query - Esempio 1
Siano = [x1 ! a1; : : : ; xn ! an] una sostituzione, Q = T1 ^ : : : ^ Tm una query
congiuntiva e O una ontologia.
e detta essere una soluzione per Q rispetto ad O se e solo se T1; : : : ;T2
compaiono in O.
Consideriamo l'ontologia O e la query Q (Chi sono gli individui con almeno un

67. glio
maschio?) de

68. nite come segue:
O = fFemale(Elise); Female(Alice); Male(Bob);
Male(Charlie); Male(Daniel);
Alice childOf Elise; Charlie childOf Elise;
Daniel childOf Alice; Daniel childOf Bob;
Francis childOf Charlieg
Q = y childOf x ^ Male(y):
Sia 1 = [x ! Alice; y ! Daniel]. 1 e una soluzione per Q rispetto ad O? SI.
Q1 = Daniel childOf Alice ^ Male(Daniel):

69. Introduzione Ontologie Interrogazioni Vocabolari
Soluzioni per una Query - Esempio 2
Siano = [x1 ! a1; : : : ; xn ! an] una sostituzione, Q = T1 ^ : : : ^ Tm una query
congiuntiva e O una ontologia.
e detta essere una soluzione per Q rispetto ad O se e solo se T1; : : : ;T2
compaiono in O.
Consideriamo l'ontologia O e la query Q de

70. nite come segue:
O = fFemale(Elise); Female(Alice); Male(Bob);
Male(Charlie); Male(Daniel);
Alice childOf Elise; Charlie childOf Elise;
Daniel childOf Alice; Daniel childOf Bob;
Francis childOf Charlieg
Q = y childOf x ^ Male(y):
Sia 2 = [x ! Alice; y ! Bob]. 2 e una soluzione per Q rispetto ad O?

71. Introduzione Ontologie Interrogazioni Vocabolari
Soluzioni per una Query - Esempio 2
Siano = [x1 ! a1; : : : ; xn ! an] una sostituzione, Q = T1 ^ : : : ^ Tm una query
congiuntiva e O una ontologia.
e detta essere una soluzione per Q rispetto ad O se e solo se T1; : : : ;T2
compaiono in O.
Consideriamo l'ontologia O e la query Q (Chi sono gli individui con almeno un

72. glio
maschio?) de

73. nite come segue:
O = fFemale(Elise); Female(Alice); Male(Bob);
Male(Charlie); Male(Daniel);
Alice childOf Elise; Charlie childOf Elise;
Daniel childOf Alice; Daniel childOf Bob;
Francis childOf Charlieg
Q = y childOf x ^ Male(y):
Sia 2 = [x ! Alice; y ! Bob]. 2 e una soluzione per Q rispetto ad O? NO.
Q2 = Bob childOf Alice ^ Male(Bob):

74. Introduzione Ontologie Interrogazioni Vocabolari
Soluzioni per una Query - Esempio 3
Siano = [x1 ! a1; : : : ; xn ! an] una sostituzione, Q = T1 ^ : : : ^ Tm una query
congiuntiva e O una ontologia.
e detta essere una soluzione per Q rispetto ad O se e solo se T1; : : : ;T2
compaiono in O.
Consideriamo l'ontologia O e la query Q de

75. nite come segue:
O = fFemale(Elise); Female(Alice); Male(Bob);
Male(Charlie); Male(Daniel);
Alice childOf Elise; Charlie childOf Elise;
Daniel childOf Alice; Daniel childOf Bob;
Francis childOf Charlieg
Q = y childOf x ^ Male(y):
Sia 3 = [x ! Charlie; y ! Francis]. 3 e una soluzione per Q rispetto ad O?

76. Introduzione Ontologie Interrogazioni Vocabolari
Soluzioni per una Query - Esempio 3
Siano = [x1 ! a1; : : : ; xn ! an] una sostituzione, Q = T1 ^ : : : ^ Tm una query
congiuntiva e O una ontologia.
e detta essere una soluzione per Q rispetto ad O se e solo se T1; : : : ;T2
compaiono in O.
Consideriamo l'ontologia O e la query Q (Chi sono gli individui con almeno un

77. glio
maschio?) de

78. nite come segue:
O = fFemale(Elise); Female(Alice); Male(Bob);
Male(Charlie); Male(Daniel);
Alice childOf Elise; Charlie childOf Elise;
Daniel childOf Alice; Daniel childOf Bob;
Francis childOf Charlieg
Q = y childOf x ^ Male(y):
Sia 3 = [x ! Charlie; y ! Francis]. 2 e una soluzione per Q rispetto ad O? NO.
Q3 = Francis childOf Charlie ^ Male(Francis):

79. Introduzione Ontologie Interrogazioni Vocabolari
Soluzioni per una Query - Esempio 4
Siano = [x1 ! a1; : : : ; xn ! an] una sostituzione, Q = T1 ^ : : : ^ Tm una query
congiuntiva e O una ontologia.
e detta essere una soluzione per Q rispetto ad O se e solo se T1; : : : ;T2
compaiono in O.
Consideriamo l'ontologia O e la query Q de

80. nite come segue:
O = fFemale(Elise); Female(Alice); Male(Bob);
Male(Charlie); Male(Daniel);
Alice childOf Elise; Charlie childOf Elise;
Daniel childOf Alice; Daniel childOf Bob;
Francis childOf Charlieg
Q = y childOf x ^ Male(y):
Sia 4 = [y ! Daniel]. 4 e una soluzione per Q rispetto ad O?