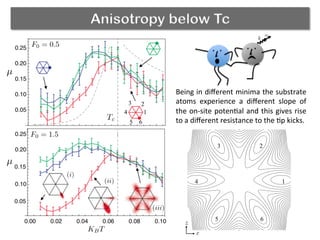
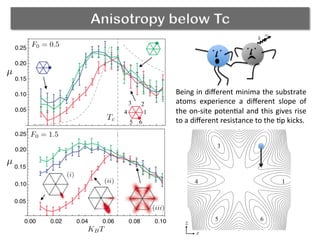
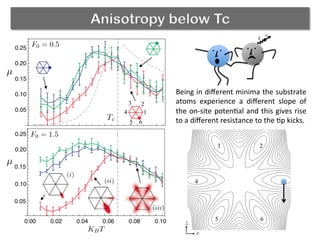
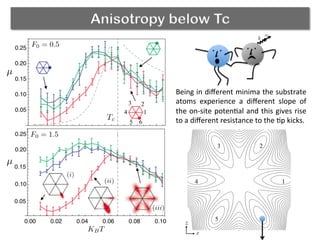
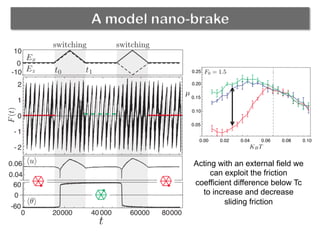
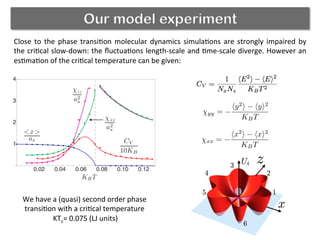
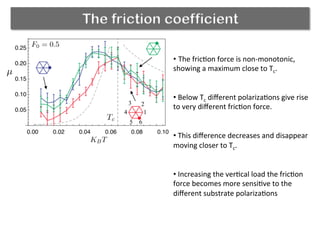
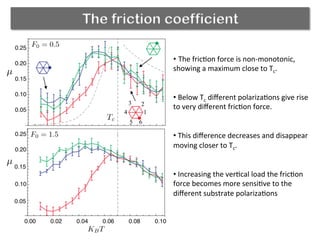
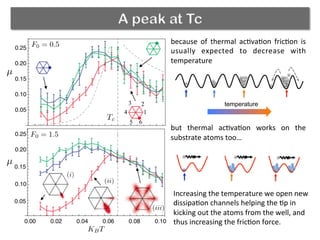
The document discusses using a phase transition in a substrate material to dynamically control friction. A molecular dynamics simulation models a 2D solid with a structural phase transition. It finds that the friction coefficient is non-monotonic near the critical temperature Tc, peaking at Tc. Below Tc, different substrate polarizations result in different friction forces, but this difference disappears near Tc. Increasing load makes friction more sensitive to polarization. The peak in friction at Tc occurs because thermal activation helps the tip kick atoms out of potential wells, aiding dissipation. Near Tc, substrate property correlations diverge, increasing damping and friction.

1. Sliding Over a Phase Transition*
Andrea Benassi
CNR-IOM Trieste and CNR-IENI Milano
*A.Benassi, A. Vanossi, G.L. Santoro and E. Tosatti PRL 106 256102 (2011)

2. A phase transition to control friction
Lubrica(on:
ü Addi(ves
ü Organic
molecule
ü Bio
molecules
Surface
modifica(on:
ü Texturing
ü Func(onaliza(on
ü Coa(ng
(SEM,DLC,…)
Mechanical
Vibra(ons

3. A phase transition to control friction
• The
sliding
bodies
always
play
a
passive
role:
we
never
exploit
the
material
physical
proper(es
• Dynamical
control
of
fric(on:
changing
fric(on
coefficient
during
sliding

4. A phase transition to control friction
Can
we
exploit
the
substrate
physical
proper(es
to
dynamically
control
fric(on?
We
need
a
substrate
with
some
tunable
material
property
Such
a
flexibility
cab
be
provided
by
the
presence
of
a
phase
transi(on

5. Some experimental evidence
The
effect
of
conductor/superconductor
transi(on
on
dissipa(on
and
fric(on
of…
...
QCM
adsorbates
Highland
&
Krim
PRL
(2006)
…pendulum
type
AFM
Kisiel
et
al.
Nature
Mat.
(2011)
Fric(on
force
microscopy
to
image
ferroelectric
domains…
FFM of TGS (Tc=49.9oC): the domain
contrast disappears approaching Tc
Bluhm,
Schwarz
&
Wiesendanger
(1998)
Eng
et
al.
(1999)
The
presence
of
domains
allows
us
to
control
the
local
value
of
the
fric(on
coefficient
using
temperature,
electric
fields
or
stress
fields.

6. Our model experiment
Uij = −U + α(|ri − rj| − a)2
+ β(|ri − rj| − a)4
Ui = UM −
2(UM − Um)
a2
0
3
xi
ui
− 4
x3
i
u3
i
u2
i +
UM − Um
a4
0
u4
i
a0
UM
Um
The
simplest
case
of
structural
phase
transi(on
is
the
ferrodistor)ve
one:
even
if
a
distor(on
of
the
la`ce
cell
take
place,
no
net
dipole
momet
arise
and
we
can
neglect
all
the
electrosta(c
interac(ons.
Despite
its
simplicity,
a
model
with
an
inter-­‐site
poten(al
+
a
mul(
well
on-­‐site
poten(al
catch
all
the
qualita(ve
features
of
a
structural
phase
transi(on.
We
studied
a
2D
solid
with
a
triangular
la`ce
and
an
on-­‐site
poten(al
with
6
wells
in
the
direc(ons
of
the
nearest
neighbors:
r uposition vector
displacement vector

7. Our model experiment
Close
to
the
phase
transi(on
molecular
dynamics
simula(ons
are
strongly
impaired
by
the
cri(cal
slow-­‐down:
the
fluctua(ons
length-­‐scale
and
(me-­‐scale
diverge.
However
an
es(ma(on
of
the
cri(cal
temperature
can
be
given:
χxx = −
x2
− x2
KBT
χyy = −
y2
− y2
KBT
We
have
a
(quasi)
second
order
phase
transi(on
with
a
cri(cal
temperature
KTc=
0.075
(LJ
units)

8. The friction coefficient
• The
fric(on
force
is
non-­‐monotonic,
showing
a
maximum
close
to
Tc.
•
Below
Tc
different
polariza(ons
give
rise
to
very
different
fric(on
force.
•
This
difference
decreases
and
disappear
moving
closer
to
Tc.
•
Increasing
the
ver(cal
load
the
fric(on
force
becomes
more
sensi(ve
to
the
different
substrate
polariza(ons

9. The friction coefficient
• The
fric(on
force
is
non-­‐monotonic,
showing
a
maximum
close
to
Tc.
•
Below
Tc
different
polariza(ons
give
rise
to
very
different
fric(on
force.
•
This
difference
decreases
and
disappear
moving
closer
to
Tc.
•
Increasing
the
ver(cal
load
the
fric(on
force
becomes
more
sensi(ve
to
the
different
substrate
polariza(ons

10. A peak at Tc
because
of
thermal
ac(va(on
fric(on
is
usually
expected
to
decrease
with
temperature
but
thermal
ac(va(on
works
on
the
substrate
atoms
too…
Increasing
the
temperature
we
open
new
dissipa(on
channels
helping
the
(p
in
kicking
out
the
atoms
from
the
well,
and
thus
increasing
the
fric(on
force.
temperature

11. A peak at Tc
Within
the
linear
response
theory
(Ying
et
al.
1990-­‐92),
the
damping
coefficient
relates
to
the
microscopic
proper(es
of
the
substrate:
close
to
a
structural
phase
transi(on,
the
correla(on
func(ons
diverges,
the
viscous
damping
too
and
goes
to
zero.
ri
r
γ =
1
KBT
ij
Si,jU(r − r0
i )U(r − r0
j )
Sij = Ft[ ri(t)rj(t
) ]

12. Anisotropy below Tc
Being
in
different
minima
the
substrate
atoms
experience
a
different
slope
of
the
on-­‐site
poten(al
and
this
gives
rise
to
a
different
resistance
to
the
(p
kicks.
k
v0
1
23
4
5 6
x
z

13. Anisotropy below Tc
Being
in
different
minima
the
substrate
atoms
experience
a
different
slope
of
the
on-­‐site
poten(al
and
this
gives
rise
to
a
different
resistance
to
the
(p
kicks.
k
v0
1
23
4
5 6
x
z

14. Anisotropy below Tc
Being
in
different
minima
the
substrate
atoms
experience
a
different
slope
of
the
on-­‐site
poten(al
and
this
gives
rise
to
a
different
resistance
to
the
(p
kicks.
k
v0
1
23
4
5 6
x
z

15. Anisotropy below Tc
Being
in
different
minima
the
substrate
atoms
experience
a
different
slope
of
the
on-­‐site
poten(al
and
this
gives
rise
to
a
different
resistance
to
the
(p
kicks.
k
v0
1
23
4
5 6
x
z

16. A model nano-brake
Acting with an external field we
can exploit the friction
coefficient difference below Tc
to increase and decrease
sliding friction

17. Conclusion
The
presence
of
a
phase
transi(on
provides
new
degrees
of
freedom
for
the
substrate
physical
proper(es
This
degrees
of
freedom
open
up
new
dissipa(on
channels
for
the
slider/(p
energy
Below
Tc
dissipa(on
and
fric(on
can
be
controlled
ac(ng
on
this
degrees
of
freedom
with
some
external
field
Model
Improvements:
• Include
dipole-­‐dipole
interac(on
(ferrodistor(ve
to
ferroelectric)
• Include
electrosta(c
(p-­‐substrate
interac(on
and
piezoelectric
response
• Beker
(p
descrip(on
Looking
for
different
kinds
of
phase
transi(on
(ferromagne(c?)
Thanks
for
your
a-en/on!