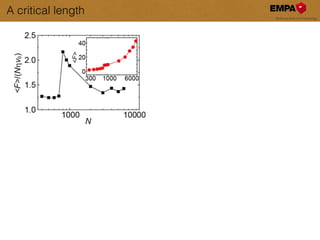
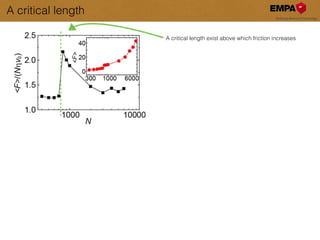
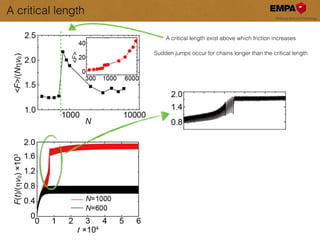
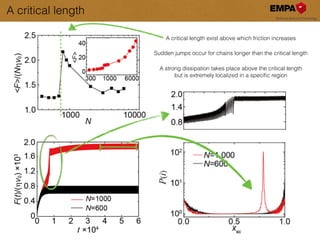
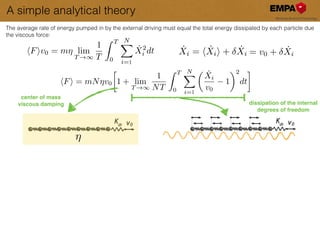
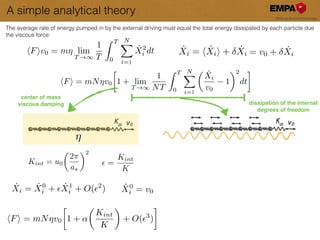
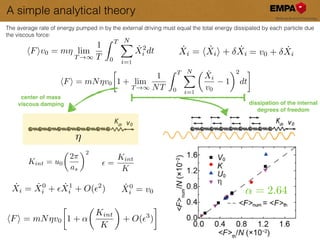
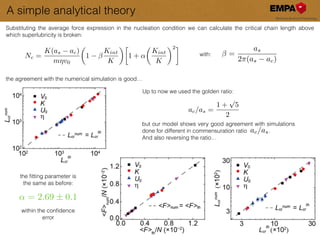
This document discusses the modeling and understanding of superlubricity in atomically precise elongated nanostructures, emphasizing the role of finite size and edge driving in disrupting the ideal superlubric state. It presents a Frenkel-Kontorova model to analyze these effects and identifies a critical chain length above which superlubricity breaks down. Furthermore, experimental validations and implications for nano-manipulation and the production of nano structures are highlighted.

1. A. Benassi !
in collaboration with M. Ma, A. Vanossi, M. Urbakh
How long can the superlubricity go?

2. New atomically precise elongated nano-structures
Progresses in nano-synthesis techniques allow to create defect free quasi 1D structures of considerable length that can be
picked up and manipulated:
Kawai et al.
PNAS 111 (2014) 3968
Polymer chains ~100nm
double-walled carbon nanotubes ~1cm
R. Zhang et al.
Nature Nanotech. 8 (2013) 912
Graphene nanoribbons ~50nm
work in progress
with Meyer & Kawai
Understanding their tribological properties is important for:
!
• Nano-manipulation and production of nano structures
for mechanics or electronics purposes
• Bringing peculiar nano-scale friction concepts at larger
scales (i.e. superlubricity)

3. The breaking of superlubricity
Assuming we can model these nanostructures as 1D incommensurate systems our Frenkel-Kontorova model must take
into account:
!
• Finite size
• Edge driving (non-uniform driving)
!!
that destroy the ideal superlubric state (in the standard Aubry sense). However, at small N, we are left with a state of very
low (dynamic) friction that we still call superlubric.
!
We know that, also for defect free systems, superlubricity is expected to vanish as we move to the macro scale:
!
Muser Europhys. Lett. 66 97 (2004) Consoli et al. PRL 85 302 (2000)
van de Ende J. Phys. Condens. Matter 24 445009 (2012)
!
Heuristically one might think that in a finite size incommensurate FK model edges plays a major role and, when N
increases, the effective stiffness of the chain decreases leaving more freedom to the edges of sitting in a minimum of the
potential increasing friction.
!
!
!
!
!
however for non-uniformly driven systems the way in which superlubricity is broken is non-trivial…
1/Keff = N/K

4. The breaking of superlubricity
Assuming we can model these nanostructures as 1D incommensurate systems our Frenkel-Kontorova model must take
into account:
!
• Finite size
• Edge driving (non-uniform driving)
!!
that destroy the ideal superlubric state (in the standard Aubry sense). However, at small N, we are left with a state of very
low (dynamic) friction that we still call superlubric.
!
We know that, also for defect free systems, superlubricity is expected to vanish as we move to the macro scale:
!
Muser Europhys. Lett. 66 97 (2004) Consoli et al. PRL 85 302 (2000)
van de Ende J. Phys. Condens. Matter 24 445009 (2012)
!
Heuristically one might think that in a finite size incommensurate FK model edges plays a major role and, when N
increases, the effective stiffness of the chain decreases leaving more freedom to the edges of sitting in a minimum of the
potential increasing friction.
!
!
!
!
!
however for non-uniformly driven systems the way in which superlubricity is broken is non-trivial…
1/Keff = N/K
- infinite size!
- incommensurate condition!
- stiff chain!
- uniform driving
zero static friction force

5. A critical length

6. A critical length
A critical length exist above which friction increases

7. A critical length
A critical length exist above which friction increases
Sudden jumps occur for chains longer than the critical length

8. A critical length
A critical length exist above which friction increases
Sudden jumps occur for chains longer than the critical length
A strong dissipation takes place above the critical length
but is extremely localized in a specific region

9. A kink of commensuration
We can define a local index of commensurability as:
and look how does it behave along the chain in time…
d(i) =
Xi Xi 1
as
A narrow region in which the chain is
commensurate nucleates at the driving edge
ad propagates up to a specific position.
!
!
The atoms pertaining to this region undergo a
regular stick-slip with strong dissipation.

10. We can define a local index of commensurability as:
and look how does it behave along the chain in time…
d(i) =
Xi Xi 1
as
A narrow region in which the chain is
commensurate nucleates at the driving edge
ad propagates up to a specific position.
!
!
The atoms pertaining to this region undergo a
regular stick-slip with strong dissipation.
A kink of commensuration

11. d(i) =
Xi Xi 1
as
P(i) = m⌘ lim
T !1
Z T
0
˙x2
i
m⌘v2
0
dt
F(t) = Kdr(V0t XN (t))
A kink of commensuration

12. d(i) =
Xi Xi 1
as
P(i) = m⌘ lim
T !1
Z T
0
˙x2
i
m⌘v2
0
dt
F(t) = Kdr(V0t XN (t))
Nucleation of the
commensuration kink
at the driving edge
incommensurate
incommensurate
commensurate
A kink of commensuration

13. A simple analytical theory
The nucleation of the kink of commensurability starts with the commensuration of the rightmost couple of atoms, the
external force needed for such a commensuration can be calculated exactly:
Fext = K(as ac) +
2⇡u0
as
sin
✓
2⇡xN
as
◆
Fmin
ext = K(as ac)
2⇡u0
as
Fmin
ext = hFi
applied to the rightmost atom, is minimum value is
the nucleation occurs when the average friction force exceed this minimum threshold
how to calculate the average friction force?

14. A simple analytical theory
The average rate of energy pumped in by the external driving must equal the total energy dissipated by each particle due
the viscous force:
hFiv0 = m⌘ lim
T !1
1
T
Z T
0
NX
i=0
˙X2
i dt
hFi = mN⌘v0

1 + lim
T !1
1
NT
Z T
0
NX
i=0
✓ ˙Xi
v0
1
◆2
dt
˙Xi = h ˙Xii + ˙Xi = v0 + ˙Xi
1
1

15. A simple analytical theory
center of mass!
viscous damping
⌘
The average rate of energy pumped in by the external driving must equal the total energy dissipated by each particle due
the viscous force:
hFiv0 = m⌘ lim
T !1
1
T
Z T
0
NX
i=0
˙X2
i dt
hFi = mN⌘v0

1 + lim
T !1
1
NT
Z T
0
NX
i=0
✓ ˙Xi
v0
1
◆2
dt
˙Xi = h ˙Xii + ˙Xi = v0 + ˙Xi
1
1

16. A simple analytical theory
center of mass!
viscous damping
⌘
dissipation of the internal !
degrees of freedom
The average rate of energy pumped in by the external driving must equal the total energy dissipated by each particle due
the viscous force:
hFiv0 = m⌘ lim
T !1
1
T
Z T
0
NX
i=0
˙X2
i dt
hFi = mN⌘v0

1 + lim
T !1
1
NT
Z T
0
NX
i=0
✓ ˙Xi
v0
1
◆2
dt
˙Xi = h ˙Xii + ˙Xi = v0 + ˙Xi
1
1

17. A simple analytical theory
center of mass!
viscous damping
⌘
dissipation of the internal !
degrees of freedom
The average rate of energy pumped in by the external driving must equal the total energy dissipated by each particle due
the viscous force:
hFiv0 = m⌘ lim
T !1
1
T
Z T
0
NX
i=0
˙X2
i dt
hFi = mN⌘v0

1 + lim
T !1
1
NT
Z T
0
NX
i=0
✓ ˙Xi
v0
1
◆2
dt
˙Xi = h ˙Xii + ˙Xi = v0 + ˙Xi
✏ =
Kint
K
˙Xi = ˙X0
i + ✏ ˙X1
i + O(✏2
) ˙X0
i = v0
hFi = mN⌘v0

1 + ↵
✓
Kint
K
◆
+ O(✏3
)
Kint = u0
✓
2⇡
as
◆2
1
1

18. A simple analytical theory
center of mass!
viscous damping
⌘
dissipation of the internal !
degrees of freedom
The average rate of energy pumped in by the external driving must equal the total energy dissipated by each particle due
the viscous force:
hFiv0 = m⌘ lim
T !1
1
T
Z T
0
NX
i=0
˙X2
i dt
hFi = mN⌘v0

1 + lim
T !1
1
NT
Z T
0
NX
i=0
✓ ˙Xi
v0
1
◆2
dt
˙Xi = h ˙Xii + ˙Xi = v0 + ˙Xi
✏ =
Kint
K
˙Xi = ˙X0
i + ✏ ˙X1
i + O(✏2
) ˙X0
i = v0
hFi = mN⌘v0

1 + ↵
✓
Kint
K
◆
+ O(✏3
)
↵ = 2.64
Kint = u0
✓
2⇡
as
◆2
1
1

19. A simple analytical theory
Substituting the average force expression in the nucleation condition we can calculate the critical chain length above
which superlubricity is broken:
the agreement with the numerical simulation is good…
Nc =
K(as ac)
m⌘v0
✓
1
Kint
K
◆
1 + ↵
✓
Kint
K
◆2
=
as
2⇡(as ac)
with:
ac/as =
1 +
p
5
2
but our model shows very good agreement with simulations
done for different in commensuration ratio .
And also reversing the ratio…
ac/as
Up to now we used the golden ratio:
the fitting parameter is
the same as before:
!
!
!
within the confidence
error
↵ = 2.69 ± 0.1

20. Testing the model with existing experiments
DWCNTs GNRs
R. Zhang et al.
Nature Nanotech. 8 (2013) 912
`c = Ncac = 0.5m
50 times > than the maximum NT size
Under investigation
Moire’ pattern
and ribbon rippling
Orientation dependent friction
Still according to static friction force measurements the
system is superlubric up to 30 nm:
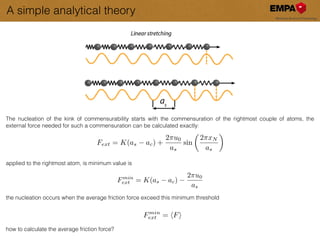
Can the edge driving
allow the nucleation
of a kink of
commensurability ?
0
0.5
1
1.5
2
2.5
0 5 10 15 20 25 30 35
peratomforce[pN]
ribbon length [nm]
Static friction force per atom VS GNR length (0 degs)
MD simulation

21. More information at:
https://sites.google.com/site/benassia/
Thank you!
Modeling material
properties !
at different length scales