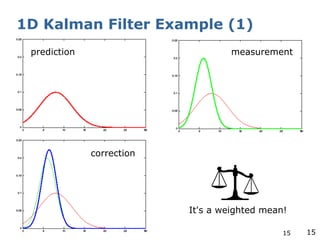
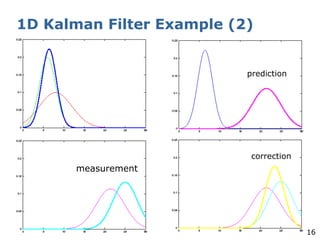
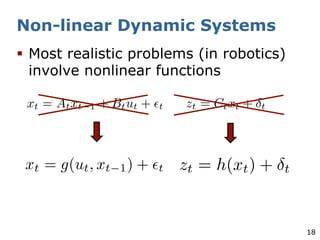
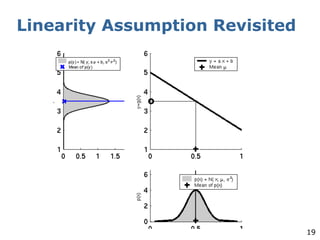
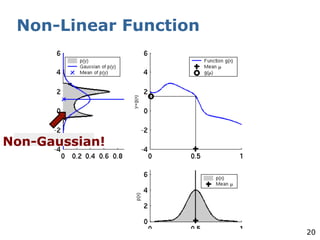
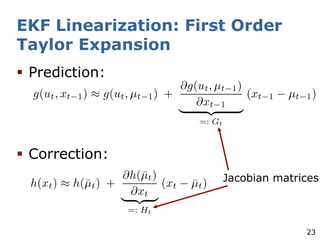
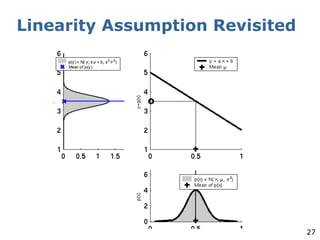
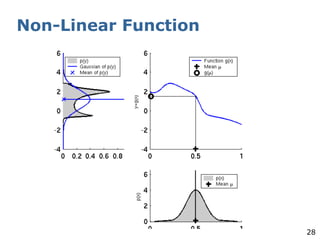
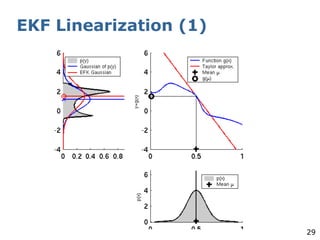
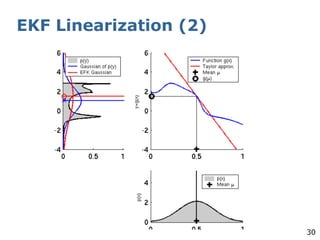
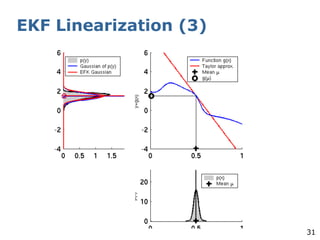
The document explains the Extended Kalman Filter (EKF) as a crucial method for addressing the simultaneous localization and mapping (SLAM) problem in robotics. It covers the principles of Kalman filters, including their assumptions of linear Gaussian models, and addresses the challenges posed by non-linear systems. The EKF is proposed as an ad-hoc solution that performs local linearizations to manage non-linearities effectively.