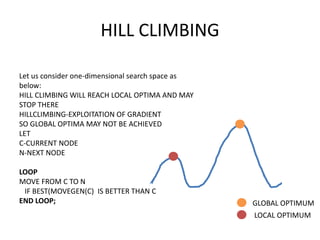
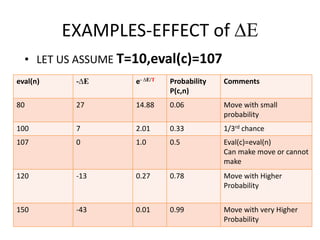
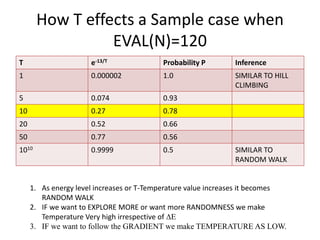
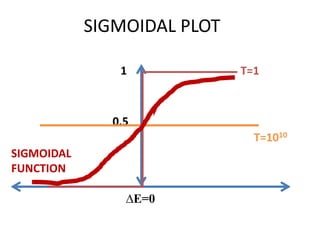
This document discusses simulated annealing, a stochastic optimization algorithm inspired by the physical annealing process. It can help avoid getting stuck in local optima like hill climbing algorithms. It works by randomly exploring different solutions and probabilistically accepting moves that decrease fitness, controlled by a temperature parameter. The probability of accepting worse moves decreases over time, guiding the search toward better solutions like hill climbing, but also allowing some exploration to avoid local optima.

1. SIMULATED ANNEALING
STOCHASTIC OR RANDOMIZED
APPROACH FOR ESCAPING LOCAL
OPTIMA
OPTIMIZATION

2. HILL CLIMBING
GLOBAL OPTIMUM
LOCAL OPTIMUM
Let us consider one-dimensional search space as
below:
HILL CLIMBING WILL REACH LOCAL OPTIMA AND MAY
STOP THERE
HILLCLIMBING-EXPLOITATION OF GRADIENT
SO GLOBAL OPTIMA MAY NOT BE ACHIEVED
LET
C-CURRENT NODE
N-NEXT NODE
LOOP
MOVE FROM C TO N
IF BEST(MOVEGEN(C) IS BETTER THAN C
END LOOP;

3. RANDOM WALK
• RANDOM WALK IS CHOOSING JUST RANDOM
NEXT NODE
• IT IS NOTHING BUT EXPLORATION

4. GOING BEYOND LOCAL OPTIMA-
APPROACHES
• TABU SEARCH
• STOCHASTIC HILL CLIMBING
• SIMULATED ANNEALING

5. OPTIMIZATION
• OPTIMIZATION IS HAPPENING IN PHYSICAL
WORLD AND NATURE
• OPTIMIZATION IN PHYSICAL WORLD
REPRESENTS THE WAY ATOMS ARE ARRANGED
IN MATERIALS
• FOR EXAMPLE IF ATOMS ARE IN ARRAY –
CRYSTALLINE STRUCTURE IS FORMED

6. OPTIMIZATION
• SO BASIC METHOD OF ACHIEVING A WELL
DEFINED PHYSICAL MATERIAL IS BY
GRADUALLY
1. HAVING A LIQUID FORM OF MATERIAL
2. AND SLOWLY COOLING IT DOWN TO FORM
MOLTEN MATERIAL
– THIS PROCESS CALLED CASTING IS USED IN
MAKING BRONZE STATUES etc…

7. Optimization
• Final form of materials- low energy materials –
minimum energy state
• Physical process of MINIMIZATION-
ANNEALING
• ANNEALING is nothing but CONTROLLED
COOLING

8. OPTIMIZATION
• HILL CLIMBING -> Generate neighbors of a
given candidate. Inspect their evaluation
Heuristic value and depending on that move
to efficient nearest neighbor->It can reach
local optima.
• RANDOM WALK-UNGUIDED.It Can choose
ANY random points-EXPLORATION
• For optimizing we need a mixture of both

9. Maximizing and Minimizing Functions
• C-> Current node
• N-> next node
• eval(c)- Fitness function of c
• eval (n)-Fitness function of n
• Maximizing function means
Move to n if eval(n)>eval(c)
• Minimizing function means
 Move to n if eval(n)<eval(c)

10. Optimization
• Take a Random Neighbour
• Then we make a decision to move to that neighbour or not
• So we take
– ∆E=eval(n)-eval(c), for maximizing
• For maximizing problems if ∆E>0 (OR) positive we will
surely make a move with HIGHER PROBABILITY
• With negative ∆E,we will still allow moves with lower
probability
• So we NEED A FUNCTION to compute probability such
that
– ∆E should influence probability
– A control variable how much ∆E should influence
probability

11. SIGMOIDAL FUNCTION
• WE WILL CHOOSE THAT FUNCTION TO BE
SIGMOIDAL
• P(c,n)=1/(1+e- ∆E/T )
• T-CONTROL VARIABLE

12. STOCHASTIC HILL CLIMBING
• n<-random neighbor(c)
• Evaluate ∆E
– ∆E=eval(n)-eval(c)
• Move with Probability
– P(c,n)=1/(1+e- ∆E/T )

13. EXAMPLES-EFFECT of ∆E
• LET US ASSUME T=10,eval(c)=107
eval(n) -∆E e- ∆E/T Probability
P(c,n)
Comments
80 27 14.88 0.06 Move with small
probability
100 7 2.01 0.33 1/3rd chance
107 0 1.0 0.5 Eval(c)=eval(n)
Can make move or cannot
make
120 -13 0.27 0.78 Move with Higher
Probability
150 -43 0.01 0.99 Move with very Higher
Probability

14. EXAMPLES-EFFECT of ∆E
• The previous table illustrates HOW
STOCHASTIC HILL CLIMBING RESPONDS TO
DIFFERENT VALUES OF ∆E
• HOW TO CHOOSE T is the next Question?
• Let us take this case which is better one and
evaluate how T effects this case:
eval(n) -∆E e- ∆E/T Probability
P(c,n)
Comments
120 -13 0.27 0.78 Move with Higher
Probability

15. How T effects a Sample case when
EVAL(N)=120
T e-13/T Probability P Inference
1 0.000002 1.0 SIMILAR TO HILL
CLIMBING
5 0.074 0.93
10 0.27 0.78
20 0.52 0.66
50 0.77 0.56
1010 0.9999 0.5 SIMILAR TO
RANDOM WALK
1. As energy level increases or T-Temperature value increases it becomes
RANDOM WALK
2. IF we want to EXPLORE MORE or want more RANDOMNESS we make
Temperature Very high irrespective of ∆E
3. IF we want to follow the GRADIENT we make TEMPERATURE AS LOW.

16. SIGMOIDAL PLOT
1
∆E=0
T=1
0.5
T=1010
SIGMOIDAL
FUNCTION

17. SIMULATED ANNEALING-ALGORITHM
• SET T<-VERY HIGH VALUE
• OUTER LOOP
– INNER LOOP
• N<-RANDOM NEIGHBOR(C)
• Evaluate ∆E
– ∆E=eval(n)-eval(c)
• Move with Probability
– P(c,n)=1/(1+e- ∆E/T )
– END INNER LOOP
– T<-MONOTONIC DECREASING FUNCTION(T)
• END OUTER LOOP

18. MONOTONIC DECREASING
FUNCTION(T)
• IT IS CALLED COOLOING RATE
• SIMPLEST IS T<-T-1