The document describes Shellsort, a sorting algorithm developed by Donald Shell in 1959. It is an improvement on insertion sort. Shellsort works by sorting elements first with large gaps between elements, then reducing the gaps and sorting again until the final gap is 1, completing the sort. It takes advantage of insertion sort being most efficient on nearly sorted lists. The time complexity is O(n^r) for 1 < r < 2, better than O(n^2) of insertion sort but generally worse than O(n log n) of quicker algorithms.

1. CSCD 300 Data Structures
Donald Shell’s Sorting Algorithm
Originally developed by Bill Clark, modified
by Tom Capaul and Tim Rolfe
1

2. Shell Sort - Introduction
More properly, Shell’s Sort
Created in 1959 by Donald Shell
Link to a local copy of the article:
Donald Shell, “A High-Speed Sorting
Procedure”, Communications of the ACM
Vol 2, No. 7 (July 1959), 30-32
Originally Shell built his idea on top of
Bubble Sort (link to article flowchart),
but it has since been transported over to
Insertion Sort.
2

3. Shell Sort -General Description
Essentially a segmented insertion sort
Divides an array into several smaller noncontiguous segments
The distance between successive elements
in one segment is called a gap.
Each segment is sorted within itself using
insertion sort.
Then resegment into larger segments
(smaller gaps) and repeat sort.
Continue until only one segment (gap = 1) final sort finishes array sorting.
3

4. Shell Sort -Background
General Theory:
Makes use of the intrinsic strengths of Insertion
sort. Insertion sort is fastest when:
The array is nearly sorted.
The array contains only a small number of
data items.
Shell sort works well because:
It always deals with a small number of elements.
Elements are moved a long way through array
with each swap and this leaves it more nearly
sorted.
4

5. Shell Sort - example
Initial Segmenting Gap = 4
80
93
60
12
42
30
68
85
10
10
30
60
12
42
93
68
85
80
5

6. Shell Sort - example (2)
Resegmenting Gap = 2
10
30
60
12
42
93
68
85
80
10
12
42
30
60
85
68
93
80
6

7. Shell Sort - example (3)
Resegmenting Gap = 1
10
12
42
30
60
85
68
93
80
10
12
30
42
60
68
80
85
93
7

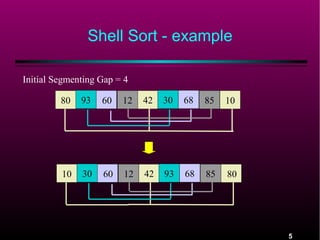
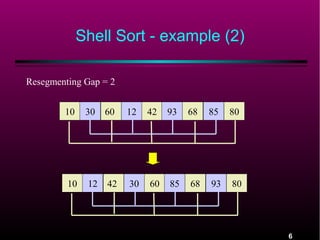
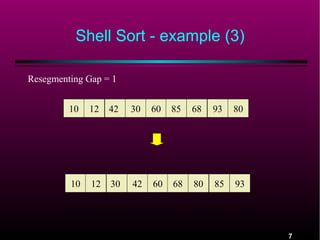
8. Gap Sequences for Shell Sort
The sequence h1, h2, h3,. . . , ht is a sequence of
increasing integer values which will be used as
a sequence (from right to left) of gap values.
Any sequence will work as long as it is increasing
and h1 = 1.
For any gap value hk we have A[i] <= A[i + hk]
An array A for which this is true is hk sorted.
An array which is hk sorted and is then hk-1
sorted remains hk sorted.
8

9. Shell Sort - Ideal Gap Sequence
Although any increasing sequence will
work ( if h1 = 1):
Best results are obtained when all values in
the gap sequence are relatively prime
(sequence does not share any divisors).
Obtaining a relatively prime sequence is often
not practical in a program so practical
solutions try to approximate relatively prime
sequences.
9

10. Shell Sort - Practical Gap Sequences
Three possibilities presented:
1) Shell's suggestion - first gap is N/2 - successive
gaps are previous value divided by 2.
Odd gaps only - like Shell method except if division
produces an even number add 1.
better performance than 1) since all odd values
eliminates the factor 2.
2.2 method - like Odd gaps method (add 1 to even
division result) but use a divisor of 2.2 and
truncate.
best performance of all - most nearly a relatively
prime sequence.
10

11. Shell Sort - Added Gap Sequence
Donald Knuth, in his discussion of Shell’s
Sort, recommended another sequence of
gaps.
h0 = 1
hj+1 = hj * 3 + 1
Find the hj > n, then start with hj/3
11

12. Link to the Java program that generated the above data.
12

13. Shell Sort - Time Complexity
Time complexity: O(nr) with 1 < r < 2
This is better than O(n2) but generally
worse than O(n log2n).
13

14. Shellsort - Code
public static void
shellSort( Comparable[ ] theArray, int n ) {
// shellSort: sort first n items in array theArray
for( int gap = n / 2; gap > 0; gap = gap / 2 )
for( int i = gap; i < n; i++ ) {
Comparable tmp = theArray[ i ];
int j = i;
for( ; j >= gap && tmp.compareTo(theArray[ j - gap ]) < 0 ; j -= gap )
theArray[ j ] = theArray[ j - gap ];
theArray[ j ] = tmp;
}
}
14

15. ShellSort -Trace (gap = 4)
[0] [1] [2]
theArray 80
n: 9
gap: 4
93
60
[3] [4] [5] [6]
[7]
[8]
12
85
10
42
30
68
i:
j:
for( int gap = n / 2; gap > 0; gap = gap / 2 )
for( int i = gap; i < n; i++ ) {
Comparable tmp = theArray[ i ];
int j = i;
for( ; j >= gap && tmp.compareTo(theArray[ j - gap ]) < 0 ; j -= gap )
theArray[ j ] = theArray[ j - gap ];
theArray[ j ] = tmp;
}
15

16. ShellSort -Trace (gap = 2)
[0] [1] [2]
theArray
[3] [4] [5] [6]
[7]
[8]
10
12
85
80
n: 9
gap: 2
30
60
42
93
68
i:
j:
for( int gap = n / 2; gap > 0; gap = gap / 2 )
for( int i = gap; i < n; i++ ) {
Comparable tmp = theArray[ i ];
int j = i;
for( ; j >= gap && tmp.compareTo(theArray[ j - gap ]) < 0 ; j -= gap )
theArray[ j ] = theArray[ j - gap ];
theArray[ j ] = tmp;
}
16

17. ShellSort -Trace (gap = 1)
[0] [1] [2]
theArray
[3] [4] [5] [6]
[7]
[8]
10
30
93
80
n: 9
gap: 1
12
42
60
85
68
i:
j:
for( int gap = n / 2; gap > 0; gap = gap / 2 )
for( int i = gap; i < n; i++ ) {
Comparable tmp = theArray[ i ];
int j = i;
for( ; j >= gap && tmp.compareTo(theArray[ j - gap ]) < 0 ; j -= gap )
theArray[ j ] = theArray[ j - gap ];
theArray[ j ] = tmp;
}
17