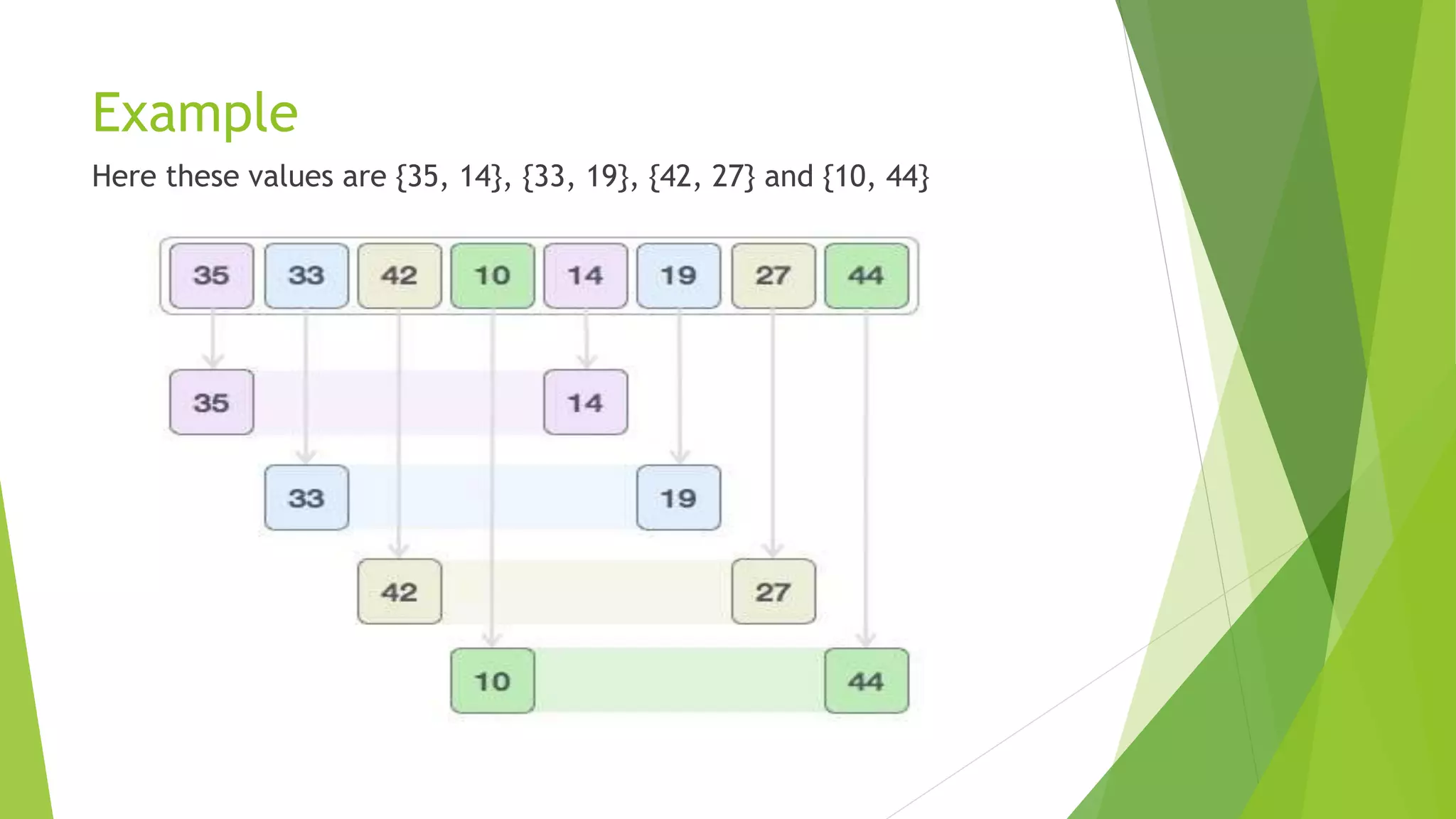
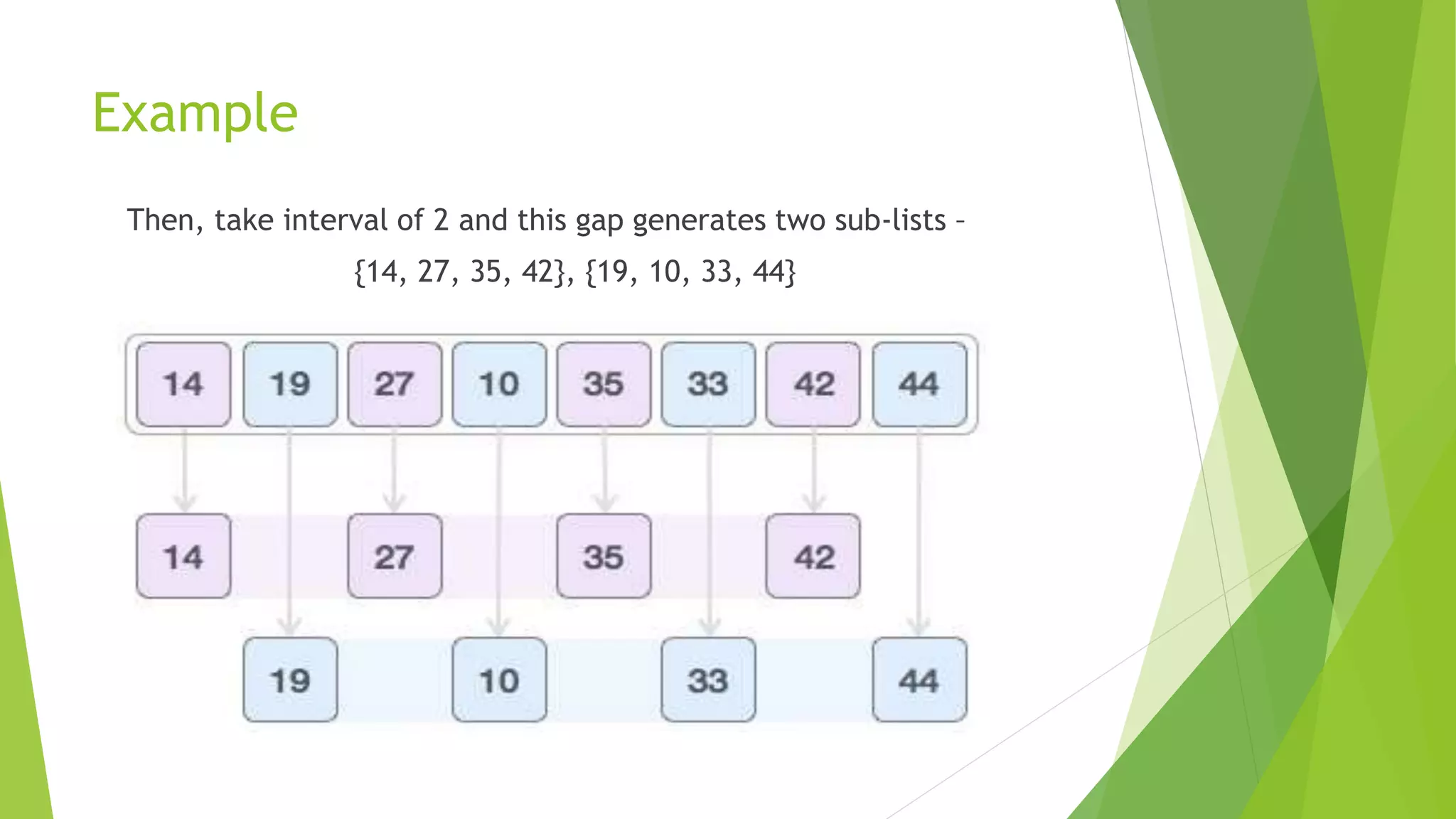
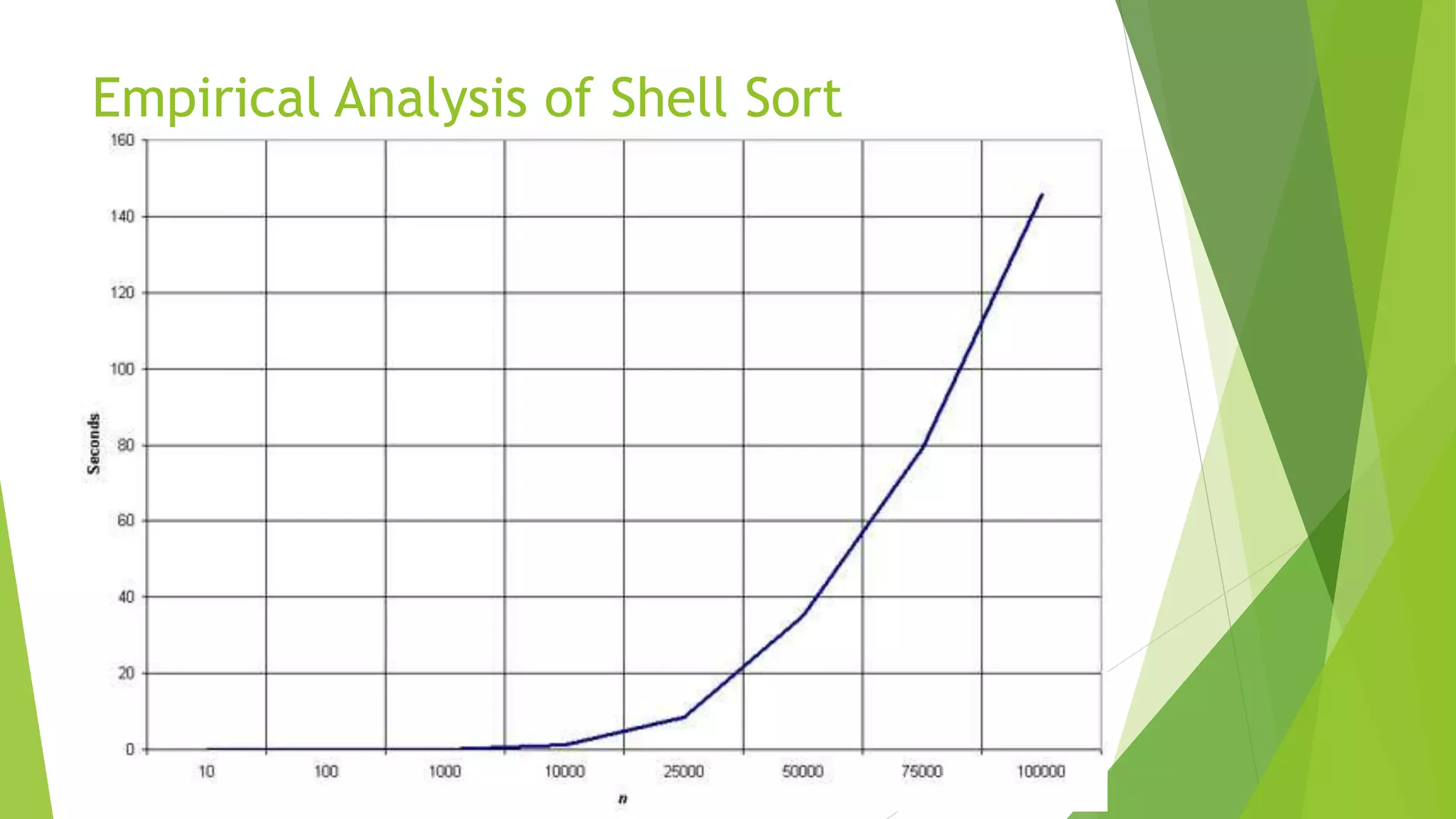
Shell sort, developed by Donald Shell in 1959, is a highly efficient sorting algorithm that minimizes the time complexity of sorting by comparing distant elements instead of adjacent ones. It operates using an increment sequence, allowing for multiple passes through a list and is generally faster than bubble and insertion sorts, though it is less efficient than merge, heap, and quick sorts. The algorithm’s performance depends on the choice of increment sequence, with its best case occurring when the array is already sorted.

1. SHELL SORT ALGORITHM

2. Shell Sort
 Founded by Donald Shell in 1959
 1st algorithm to break the quadratic time barrier
 a highly efficient sorting algorithm
 known as diminishing increment sort
 Generalization of insertion short

3. How does Shell Sort Works?
 works by comparing elements that are distant rather than
adjacent elements in an array or list where adjacent elements are
compared
 uses increment sequence
 makes multiple passes through a list
 improves on the efficiency of insertion sort
 decreases distance between comparisons

4. Example
Here these values are {35, 14}, {33, 19}, {42, 27} and {10, 44}

5. Example
Compare values in each sub-list and swap them (if necessary) in the
original array. After this step, the new array should look like this −

6. Example
Then, take interval of 2 and this gap generates two sub-lists –
{14, 27, 35, 42}, {19, 10, 33, 44}

7. Example
Again, compare and swap the values, if required, in the original array.
After this step, the array should look like this −
Finally, the rest of the array sorted using interval of value 1. Shell
sort uses insertion sort to sort the array.

8. Example
We see that it
required only four
swaps to sort the rest
of the array.

9. Empirical Analysis of Shell Sort

10. Empirical Analysis of Shell Sort
(Advantage)
 Fastest of all O (N^2) sorting algorithms
 it’s only efficient for medium size lists
 Five (5) times faster than the bubble sort
 a little over twice as fast as the insertion sort

11. Empirical Analysis of Shell Sort
(Dis-advantage)
 it is a complex algorithm
 it’s not nearly as efficient as the merge, heap, and quick sorts
 still significantly slower than the merge, heap, and quick sorts
 also an excellent choice for repetitive sorting of smaller lists.

12. Shell Sort Best Case
 when the array is already sorted in the right order
 the number of comparisons is less.
Shell Sort Worst Case
 running time of Shell sort depends on the choice of increment
sequence.
 pairs of increments are not necessarily relatively prime and smaller
increments can have little effect.