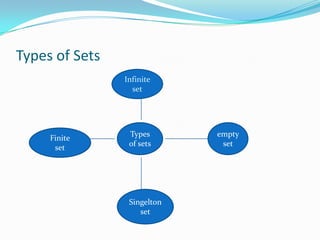
This document defines and provides examples of sets and related concepts: - A set is a well-defined collection of objects, called elements or members. Sets are denoted by capital letters and elements by lowercase letters. - There are four main types of sets: empty sets which have no elements; singleton sets with one element; finite sets with a countable number of elements; and infinite sets with an uncountable number of elements. - Subsets contain all the elements of another set. A proper subset excludes at least one element, while an improper subset is equal to the other set. The universal set is the largest set of which all other sets are subsets.

1. Compiled by
Prof . Sandeep
Gupta

3. Meaning
 Set is a WELL DEFINED collection of objects

4. Meaning

5. Meaning
Bag is a set which consists of well defined
Objects i.e. pencils, erasers, scale,
books etc. These objects are the elements of
this set

6. Examples

7. Examples
Can a beautiful girl or group of beautiful girls be
a set?

8. Examples
The answer is ‘NO’
because beauty is not well defined

9. Examples
Can a group of boys be a collection of Set?
‘YES’ , group of boys is a set because number
of boys in the group are well defined

10. Ur turn to think…..
A smart man …. Is it a Set?
Ans. ………

11. Examples
Group of good teachers in school…….is it a
collection of set?
Ans………

12. Examples
Collection of prime numbers?
Ans…….

13. SETS
 Indiviual object in the set is called ELEMENT or a
MEMBER of the set.
 Sets are denoted by capital alphabets , e.g. A, B, C etc.
 Elements of set are denoted by small alphabets , e.g. a,
b, c etc.
 If a is an element of set X then we write it as a Є X
 If a is not an element of set X, then it is written as a Є X

14. Types of Sets
Types
of sets
empty
set
Singelton
set
Finite
set
Infinite
set

15. Types of Sets
 Empty set : it’s a set having no element. Also known as
Null set, it is denoted by Ф
 Singleton set : it’s a set having only one element
 Finite set : it’s a set wherein counting of elements ends
at a certain stage
 Infinite set : it’s a set in which counting of elements do
not end at any stage
 An empty set is a finite set
 Natural and whole numbers, integers, rational and real
numbers are infinite sets

16. Few concepts worth remembering
 Natural and Whole numbers
 these includes numbers like 1,2,3,4 etc
only difference is we include ‘0’ (zero) in whole
numbers but not in natural numbers
are not fractions, decimals or negative numbers
 Integers
 are positive or negative numbers and includes zero
are whole numbers but can be negative too

17. Few concepts worth remembering
 Rational numbers
Includes integers, fractions and repeating decimals
• Irrational numbers
Includes only decimals that have no pattern and continue
forever
• Real numbers
It includes every thing discussed above

18. Symbols
Symbols commonly used:
Whole numbers W
Integers I
Rational numbers Q
Natural numbers N
Real numbers R

19. Methods of writing sets
 Listing method (Roster form)
 Rule method (Set builder form)
Examples
1. Set of first 20 even natural numbers
Roster form
A = {2, 4, 6, 8, ………40}
Set builder form
A = {x|x is even natural number, 2 ≤ x ≤ 40}

20. Examples
Example 2
Set of first 10 multiples of 5
Roster form
A = {5, 10, 15, 20, …..50}
Set builder form
A = {x|x=5n, n Є N, 1 ≤ n ≤ 10}

21. Concept of Subsets
 If every element of set B is an element of set A, then
set B is subset of set A
 Subset can be proper subset or improper subset
 If set B is subset of set A and set A contains at least one
element which is not in set B, then set B is proper
subset of set A
 If set A is subset of set B and if set B is subset of set A,
then they are improper subsets of each other
 B A is to be read as set B is proper subset of set A

22. Concepts of subsets
 A B is to be read as set A is super set of set B
 A B is to be read as set A is improper subset of set
B
 Every set is subset of itself
 Empty set is subset of every set

23. Universal set
 A non-empty set of which all the sets under
consideration are the subsets of that set is called
universal set
 It is denoted by ‘U’

24. The
End