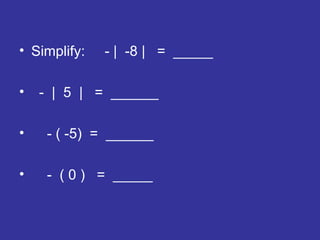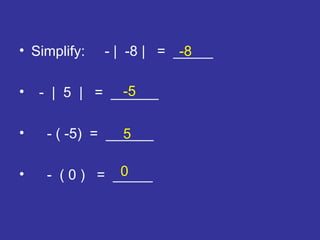The document is a lesson on integers from a math textbook. It covers topics like the integer number line, comparing integers using less than/greater than symbols, ordering integers from least to greatest, opposites, absolute value, and simplifying expressions with integers. It provides examples and practice problems for students to learn about properties of integers and how to perform operations with positive and negative numbers.

1. Lesson 2.1 , For use with pages 57-61 Copy and complete the statement with < or > . 1. 27 ? 13 2. 15 ? 51 3. 6 ? 0

2. Lesson 2.1 , For use with pages 57-61 Copy and complete the statement with < or > . ANSWER < ANSWER > ANSWER > 1. 27 ? 13 2. 15 ? 51 3. 6 ? 0

3. Math Tests

4. Awards

5. Standards and Benchmarks 8.2.4

6. Chapter 2 Integers Understanding the four operations using positive and negative numbers

7. In this chapter you will also learn about and work with the coordinate plane, numerous number properties, opposites, absolute value, reciprocals, and the various sets of numbers in our INTEGER number set.

8. Integers and Absolute Value Section 2.1 P. 57 The students will learn to compare integers and simplify expressions.

9. Integers The set of integers can be described as all the whole numbers and their opposites. Integers = { . . . -3, -2, -1, 0, 1, 2, 3, . . . } Number line: - 3 - 1 0 1 3

10. Section 2.1 The INTEGER Number Line Negative ORIGIN Positive Zero is a neutral number. It NEVER carries a positive or negative sign. ____ + 0

11. Graph the following numbers: -4, 0, 1, -2 Plotting a point on the number line means the point has been graphed . Put the numbers in order from least to greatest -4 -3 -2 -1 0 1 2 3 4

12. Two points that are the same distance from the origin but on opposite sides (of the origin) are opposites . Name some opposites on this #-line -4 -3 -2 -1 0 1 2 3 4

13. Sometimes it is good to think of money or temperatures when comparing positive & negatives numbers. Positive -- a gain, an increase - others? Negative – a loss, a decrease, --??

14. Order these numbers from least to greatest: -35, 18, 75, -53, -39, 62, 7, 0 Put > or < sign 6 ___ -4 - 4 _____0 5_____-5 -37 ____-39 -9 _____9 -2 ____-8 > > < < > >

15. Order these numbers from least to greatest: -35, 18, 75, -53, -39, 62, 7, 0 Put > or < sign 6 ___ -4 - 4 _____0 5_____-5 -37 ____-39 -9 _____9 -2 ____-8

16. Hint: When the negative is next to a number it is read as a negative. (-3) When the negative sign is outside the parenthesis it is read as “the opposite of.” –(3) The expression “ (-3)” can be stated as “negative three” and the expression “-(3)” can be stated as “the opposite of three” Does zero have an opposite? - (-4) = _____ - [ -(-5)] = _____

17. Hint: When the negative is next to a number it is read as a negative. (-3) When the negative sign is outside the parenthesis it is read as “the opposite of.” –(3) The expression “ (-3)” can be stated as “negative three” and the expression “-(3)” can be stated as “the opposite of three” Does zero have an opposite? - (-4) = _____ - [ -(-5)] = _____ 4 -5

18. Absolute Value The absolute value of a real number is the distance between the origin and the point representing the number. The symbol | a | represents the absolute value of a . The absolute value of a number is never negative.

19. Note: ABSOLUTE VALUE is NOT the same as OPPOSITE. They both have different meanings when working with the INTEGERS. This is often a common mistake for students.

20. Examples: | 6 | = _______ | 0 | = _______ | -5 | = _______ | -32 | = _______ | 52 | = _______

21. Examples: | 6 | = _______ | 0 | = _______ | -5 | = _______ | -32 | = _______ | 52 | = _______ 0 6 5 52 32

22. Simplify: - | -8 | = _____ - | 5 | = ______ - ( -5) = ______ - ( 0 ) = _____

23. Simplify: - | -8 | = _____ - | 5 | = ______ - ( -5) = ______ - ( 0 ) = _____ -8 -5 5 0

24. Assignment P. 59 #1, 2-20 evens , 21 – 32 all Read directions carefully!!