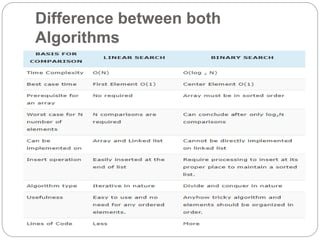
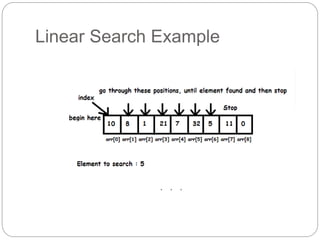
The document discusses linear and binary search algorithms. Linear search is the simplest algorithm that sequentially compares each element of an array to the target element. It has a worst case time complexity of O(N). Binary search works on a sorted array by comparing the middle element to the target. It eliminates half of the remaining elements with each comparison. It has a worst case time complexity of O(log n), which is faster than linear search for large data sets. Pseudocode and C programs are provided as examples to implement linear and binary search.

1. By: Er. Anupam Sharma
Assistant Professor in CSE
Searching

2. Linear search
Linear search is the simplest searching algorithm
which is sometimes known as sequential search.
In this algorithm each element of array is
compared with the targeted element sequentially.
Worst Case Time Complexity -O(N)
Best Case Time Complexity: O(1)

3. Linear Search Algorithm
Linear Search ( Array A, Value x)
Step 1: Set i to 1
Step 2: if i > n then go to step 7
Step 3: if A[i] = x then go to step 6
Step 4: Set i to i + 1
Step 5: Go to Step 2
Step 6: Print Element x Found at index i and go to step 8
Step 7: Print element not found
Step 8: Exit

4. Pseudocode for Linear Search
procedure linear_search (list, value)
for each item in the list
if match item == value
return the item's location
end if
end for
end procedure

5. Linear Search Example

6. Program for Linear Search in C
#include<stdio.h>
int main()
{
int a[20],i,x,n;
printf("How many elements?");
scanf("%d",&n);
printf("Enter array elements:n");
for(i=0;i<n;++i)
scanf("%d",&a[i]);
printf("nEnter element to search:");
scanf("%d",&x);
for(i=0;i<n;++i)
if(a[i]==x)
break;
if(i<n)
printf("Element found at index %d",i);
else
printf("Element not found");
return 0;
}
Output
How many elements?4
Enter array elements:
6 8 9 1
Enter element to
search:9
Element found at index
2

7. Binary Search
Binary search algorithm can be applied on a sorted array
to search an element. Search begins with comparing
middle element of array to target element. If both are
equal then position of element is returned. If target
element is less than middle element of array then upper
half of array is discarded and again search continued by
dividing the lower half. If target element is greater than
middle element then lower half is discarded and search is
continued in upper half.
 Worst Case Time Complexity: O(log n)
 Best Case Time Complexity: O(1)

8. Binary Search Algorithm
 Following are the steps of implementation that we will
be following:
 Start with the middle element:
 If the target value is equal to the middle element of the
array, then return the index of the middle element.
 If not, then compare the middle element with the target
value,
 If the target value is greater than the number in the middle
index, then pick the elements to the right of the middle index,
and start with Step 1.
 If the target value is less than the number in the middle index,
then pick the elements to the left of the middle index, and start
with Step 1.
 When a match is found, return the index of the
element matched.

9. Pseudo code for Binary Search
Procedure binary_search
A ← sorted array
n ← size of array
x ← value to be searched
Set lowerBound = 1
Set upperBound = n
while x not found
if upperBound < lowerBound
EXIT: x does not exists.
set midPoint = lowerBound + ( upperBound - lowerBound ) / 2
if A[midPoint] < x set lowerBound = midPoint + 1
if A[midPoint] > x set upperBound = midPoint - 1
if A[midPoint] = x EXIT: x found at location midPoint
end while
end procedure

10. Example

11. #include <stdio.h>
int main()
{ int c, first, last, middle, n, search, array[100];
printf("Enter number of elementsn");
scanf("%d",&n);
printf("Enter %d integersn", n);
for (c = 0; c < n; c++)
scanf("%d",&array[c]);
printf("Enter value to findn");
scanf("%d", &search);
first = 0; last = n - 1;
middle = (first+last)/2;
while (first <= last) {
if (array[middle] < search)
first = middle + 1;
else if (array[middle] == search) {
printf("%d found at location %d.n", search, middle+1);
break; }
else
last = middle - 1;
middle = (first + last)/2; }
if (first > last)
printf("Not found! %d isn't present in the list.n", search);
return 0; }
Program for Binary Search in
C

12. Difference between both
Algorithms