Scala. Introduction to FP. Monads

Scala. Introduction to FP.
Monads.
k.v.kozlov@gmail.com, 2015

Functions as Objects
What about functions?
In fact function values are treated as objects in Scala.
The function type A => B is just an abbreviation for the class
scala.Function1[A, B], which is deﬁned as follows.
package scala
trait Function1[A, B] {
def apply(x: A): B
}
So functions are objects with apply methods.

An anonymous function such as
(x: Int) => x * x
is expanded to:
{
class AnonFun extends Function1[Int, Int] {
def apply(x: Int) = x * x
}
new AnonFun
}
or, shorter, using anonymous class syntax:
new Function1[Int, Int] {
}

A function call, such as f(a, b), where f is a value of some class
type, is expanded to
f.apply(a, b)
So the OO-translation of
val f = (x: Int) => x * x
f(7)
would be
val f = new Function1[Int, Int] {
}
f.apply(7)

Case Classes
A case class definition is similar to a normal class
definition, except that it is preceded by the
modifier case. For example:
trait Expr
case class Number(n: Int) extends Expr
case class Sum(e1: Expr, e2: Expr) extends Expr
Like before, this defines a trait Expr, and two
concrete subclasses
Number and Sum

Case Classes
It also implicitly deﬁnes companion objects with apply
methods.
object Number {
def apply(n: Int) = new Number(n)
}
object Sum {
def apply(e1: Expr, e2: Expr) = new Sum(e1, e2)
}
so you can write Number(1) instead of new Number(1).

Pattern matching
Pattern matching is a generalization of switch from C/Java to
class hierarchies.
It’s expressed in Scala using the keyword match.
Example
eval(Sum(Number(1), Number(2)))
def eval(e: Expr): Int = e match {
case Number(n) => n
case Sum(e1, e2) => eval(e1) + eval(e2)
}

Lists
The list is a fundamental data stucture in functional programming.
A list having x1, ...,xn as elements is written List(x1, ...,xn)
Example
val fruit = List(«apples», «oranges», «pears»)
val nums = List(1, 2, 3, 4)
val diag3 = List(List(1, 0, 0), List(0, 1, 0), List(0, 0, 1))
val empty = List()
There are two important differences between lists and arrays.
● List are imuttable - the elements of list cannot be changed
● Lists are recursive, while arrays are flat

Constructors of Lists
All lists are constructed from:
● The empty list Nil, and
● The constructor operation :: (pronounces cons):
x :: xs gives a new list with the first element x, followed
by the element of xs
Example
fruit = «apples» :: («oranges» :: («pears» :: Nil))
nums = 1 :: (2 :: (3 :: (4 :: Nil)))
empty = Nil

Map
A simple way to define map is as follows:
abstract class List[T] { ...
def map[U](f: T => U): List[U] = this match {
case Nil => Nil
case x :: xs => f(x) :: xs.map(f)
}
Example
def scaleList(xs: List[Double], factor: Double) =
xs map (x => x * factor)

flatMap
abstract class List[T] {
def flatMap[U](f: T => List[U]): List[U] = this match {
case x :: xs => f(x) ++ xs.flatMap(f)
case Nil => Nil
}
}

Filter
This pattern is generalized by the method filter of the List class:
abstract class List[T] {
...
def filter(p: T => Boolean): List[T] = this match {
case Nil => Nil
case x :: xs => if (p(x)) x :: xs.filter(p) else xs.filter(p)
}
}
Example
def posElems(xs: List[Int]): List[Int] =
xs filter (x => x > 0)

For-Expression
Higher-order functions such as map, flatMap
or filter provide powerful constructs for
manipulating lists.
But sometimes the level of abstraction
required by these function make the program
difficult to understand.
In this case, Scala's for expression notation
can help.

For-Expression Example
Let person be a list of elements of class Person, with fields
name and age.
case class Person(name: String, age: Int)
To obtain the names of person over 20 years old, you can
write:
for ( p <- persons if p.age > 20 ) yield p.name
Which is equivalent to:
persons filter (p => p.age > 20) map (p => p.name)
The for-expression is similar to loops in imperative languages,
except that is builds a list of the result of all iterations.

Syntax of For
A for-expression is of the form:
for ( s ) yield e
where s is a sequence of generators and filters, and e is an expression whose value is
returned by an iteration.
●
A generator is of the form p <- e, where p is a pattern and e an expression whose value is a
collection.
●
A filter is of the form if f where f is a boolean expression.
●
The sequence must start with generator.
●
If there are several generators in the sequence, the last generators vary faster than the first.
Example
for {
i <- 1 until n
j <- 1 until i
if isPrime(i + j)
} yield (i, j)

Queries with for
case class Book(title: String, authors: List[String])
val books: List[Book] = List(
Book(title = ”Structure and Interpretation of Computer Programs”,
authors = List(”Abelson, Harald”, ”Sussman, Gerald J.”)),
Book(title = ”Introduction to Functional Programming”,
authors = List(”Bird, Richard”, ”Wadler, Phil”)),
Book(title = ”Effective Java”,
authors = List(”Bloch, Joshua”)),
Book(title = ”Java Puzzlers”,
authors = List(”Bloch, Joshua”, ”Gafter, Neal”)),
Book(title = ”Programming in Scala”,
authors = List(”Odersky, Martin”, ”Spoon, Lex”, ”Venners, Bill”)))
To find the names of all authors who have written at least two books present in the database:
for {
b1 <- books
b2 <- books
if b1.title < b2.title
a1 <- b1.authors
a2 <- b2.authors
if a1 == a2
} yield a1

For-Expressions and Higher-Order
Functions
The syntax of for is closely related to the higher-order
functions map, flatMap and filter.
First of all, these functions can all be defined in terms of for:
def map[T, U](xs: List[T], f: T => U): List[U] =
for (x <- xs) yield f(x)
def flatMap[T, U](xs: List[T], f: T => Iterable[U]): List[U] =
for (x <- xs; y <- f(x)) yield y
def filter[T](xs: List[T], p: T => Boolean): List[T] =
for (x <- xs if p(x)) yield x
And vice versa

Translation of For
In reality, the Scala compiler expresses for-
expression in terms of map, flatMap and a lazy
variant of filter.
1. A simple for expression
for (x <- e1) yield e2
is translated to
e1.map(x => e2)

Translation of For
2: A for-expression
for (x <- e1 if f; s) yield e2
where f is a filter and s is a (potentially empty)
sequence of generators and filters, is translated to
for (x <- e1.withFilter(x => f); s) yield e2
(and the translation continues with the new expression)
You can think of withFilter as a variant of filter that
does not produce an intermediate list, but instead
filters the following map or flatMap function application.

Translation of For
3: A for-expression
for (x <- e1; y <- e2; s) yield e3
where s is a (potentially empty) sequence of
generators and ﬁlters,
is translated into
e1.flatMap(x => for (y <- e2; s) yield e3)
(and the translation continues with the new
expression)

Example
Take the for-expression that computed pairs whose sum is
prime:
for {
i <- 1 until n
j <- 1 until i
if isPrime(i + j)
} yield (i, j)
Applying the translation scheme to this expression gives:
(1 until n).flatMap(i =>
(1 until i).withFilter(j => isPrime(i+j))
.map(j => (i, j)))

For and Databases
For example, books might not be a list, but a database stored on
some server.
As long as the client interface to the database deﬁnes the methods
map, flatMap and withFilter, we can use the for syntax for querying
the database.
This is the basis of the Scala data base connection frameworks
ScalaQuery and Slick.
Similar ideas underly Microsoft’s LINQ(for (c < -coffees;
if c.sales > 999
)yield c.nam e).run
select"CO F_NAM E"
from "CO FFEES"
w here "SALES" > 999

Coffee break
As soon as you understand Monads, you will understand that
this is a Monad, too.
{{alt: What if someone broke out of a hypothetical situation in
your room right now?}}

Monads
Data structures with map and flatMap seem to
be quite common.
In fact there’s a name that describes this class
of a data structures together with some
algebraic laws that they should have.
They are called monads.

What is a Monad?
A monad M is a parametric type M[T] with two
operations, flatMap and unit, that have to satisfy
some laws.
trait M[T] {
def flatMap[U](f: T => M[U]): M[U]
}
def unit[T](x: T): M[T]
In the literature, flatMap is more commonly
called bind.

Examples of Monads
– List is a monad with unit(x) = List(x)
– Set is monad with unit(x) = Set(x)
– Option is a monad with unit(x) = Some(x)
– Generator is a monad with unit(x) = single(x)
– …......
flatMap is an operation on each of these
types, whereas unit in Scala is di erent forﬀ
each monad.

Monads and map
map can be deﬁned for every monad as a
combination of flatMap and unit:
m map f
== m flatMap (x => unit(f(x)))
== m flatMap (f andThen unit)

Monad Laws
To qualify as a monad, a type has to satisfy
three laws:
Associativity
m flatMap f flatMap g == m flatMap (x => f(x) flatMap g)
Left unit
unit(x) flatMap f == f(x)
Right unit
m flatMap unit == m

The Option monad
sealed trait Option[A] {
def map[B](f: A => B): Option[B]
def flatMap[B](f: A => Option[B]): Option[B]
}
case class Some[A](a: A) extends Option[A]
case class None[A] extends Option[A]
The Option monad makes the possibility of
missing data explicit in the type system, while
hiding the boilerplate «if non-null» logic

Checking Monad Laws
Let’s check the monad laws for Option.
Here’s flatMap for Option:
abstract class Option[+T] {
def flatMap[U](f: T => Option[U]): Option[U] = this match
{
case Some(x) => f(x)
case None => None
}
}

Try
Try resembles Option, but instead of Some/None
there is a Success case with a value and a Failure
case that contains an exception:
abstract class Try[+T]
case class Success[T](x: T) extends Try[T]
case class Failure(ex: Exception) extends Try[Nothing]
Try is used to pass results of computations that
can fail with an exception between threads and
computers

Creating a Try
You can wrap up an arbitrary computation in a Try.
Try(expr) // gives Success(someValue) or Failure(someException)
Here’s an implementation of Try:
object Try {
def apply[T](expr: => T): Try[T] =
try Success(expr)
catch {
case NonFatal(ex) => Failure(ex)
}
}

Composing Try
Just like with Option, Try-valued computations can be composed
in for
expresssions.
for {
x <- computeX
y <- computeY
} yield f(x, y)
If computeX and computeY succeed with results Success(x) and
Success(y), this will return Success(f(x, y)).
If either computation fails with an exception ex, this will return
Failure(ex).

Deﬁnition of flatMap and map on Try
abstract class Try[T] {
def flatMap[U](f: T => Try[U]): Try[U] = this match {
case Success(x) => try f(x) catch { case NonFatal(ex) => Failure(ex) }
case fail: Failure => fail
}
def map[U](f: T => U): Try[U] = this match {
case Success(x) => Try(f(x))
case fail: Failure => fail
}
}
The Try monad makes the possibility of errors explicit in
the type system, while hiding the boilerplate «try/catch»
logic

We have seen that for-expressions are useful not only for collections. Many other types
also define map,flatMap, and withFilter operations and with them for-expressions.
Examples: Generator, Option, Try.
Many of the types defining flatMap are monads.
(If they also define withFilter, they are called “monads with zero”).
The three monad laws give useful guidance in the design of library APIs.

Reactive manifesto
[Merriam Webster] reactive: “readily responsive to a stimulus”.
▶ React to events (event-driven)
▶ React to load (scalable)
▶ React to failures (resilient)
▶ React to users (responsive)

Lets play a simple game:
trait Adventure {
def collectCoins(): List[Coin]
def buyTreasure(coins: List[Coin]): Treasure
}
val adventure = Adventure()
val coins = adventure.collectCoins()
val treasure = adventure.buyTreasure(coins)

Actions may fail
def collectCoins(): List[Coin] = {
if (eatenByMonster(this))
throw new GameOverException(“Ooops”)
List(Gold, Gold, Silver)
}
def buyTreasure(coins: List[Coin]): Treasure = {
if (coins.sumBy(_.value) < treasureCost)
throw new GameOverException(“Nice try!”)
Diamond
}

Sequential composition of actions
that may fail
// block until coins are collected
// only continue if there is no exception
// block until treasure is bought

Expose possibility of failure in the
types, honestly
T => S
T => Try[S]

Making failure evident intypes
import scala.util.{Try, Success, Failure}
abstract class Try[T]
case class Success[T](elem: T) extends Try[T]
case class Failure(t: Throwable) extends Try[Nothing]
object Try {
def apply[T](r: =>T): Try[T] = {
try { Success(r) }
catch { case t => Failure(t) }
}
trait Adventure {
def collectCoins(): Try[List[Coin]]
def buyTreasure(coins: List[Coin]): Try[Treasure]
}

Dealing with failure explicitly
val coins: Try[List[Coin]] = adventure.collectCoins()
val treasure: Try[Treasure] = coins match {
case Success(cs) adventure.buyTreasure(cs)⇒
case failure @ Failure(t) failure⇒
}

Noise reduction
val treasure: Try[Treasure] =
adventure.collectCoins().flatMap(coins {⇒
adventure.buyTreasure(coins)
})
val treasure: Try[Treasure] = for {
coins <- adventure.collectCoins()
treasure <- buyTreasure(coins)
} yield treasure

Amonad that handles exceptions.
Try[T]
The Try monad makes the possibility of errors
explicit in the type system, while hiding the
boilerplate «try/catch» logic

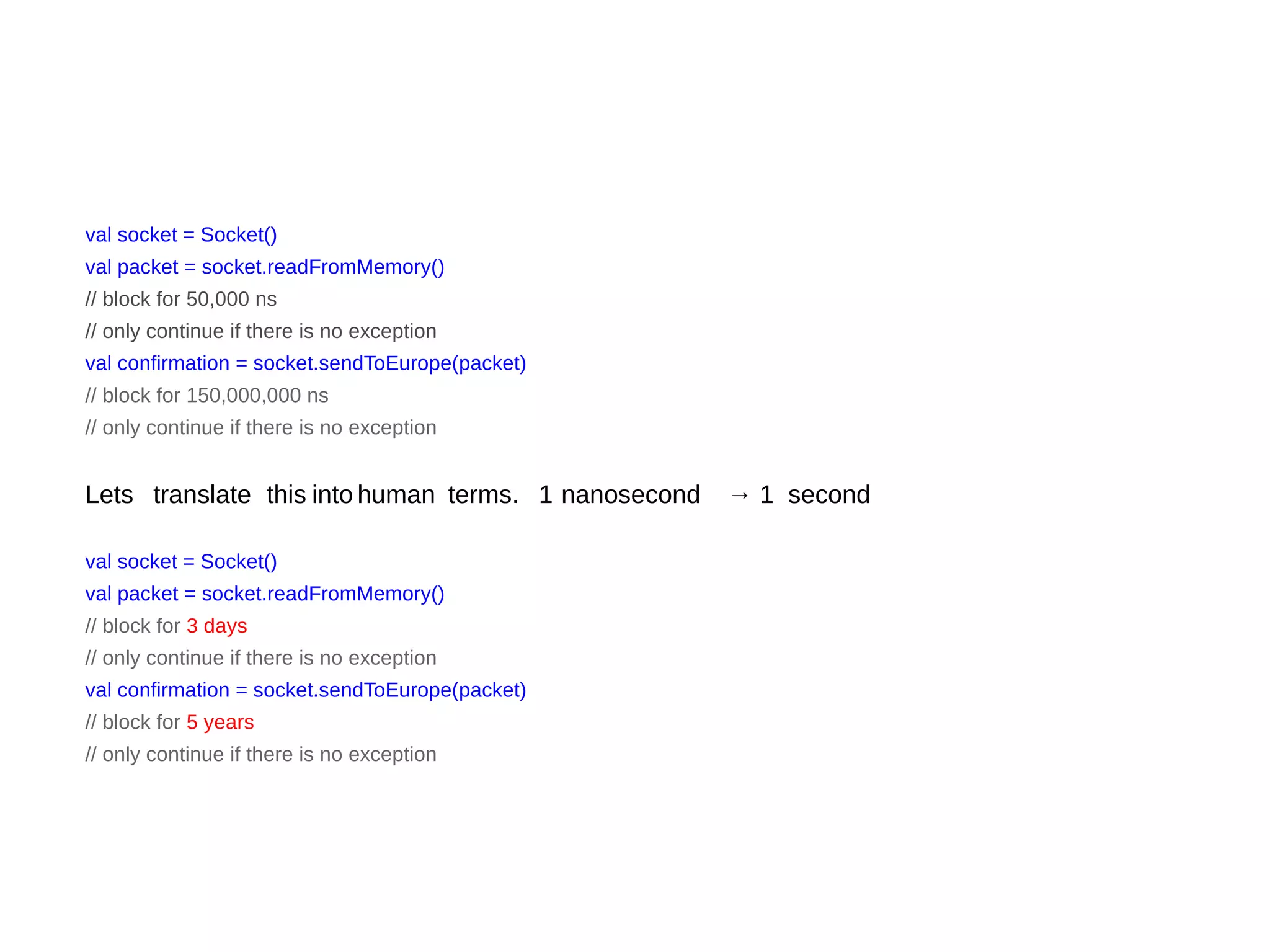
trait Socket {
def readFromMemory(): Array[Byte]
def sendToEurope(packet: Array[Byte]): Array[Byte]
}
val socket = Socket()
val packet = socket.readFromMemory()
val confirmation = socket.sendToEurope(packet)

Timings for various operations on
a typical PC

// block for 50,000 ns
// block for 150,000,000 ns
Lets translate this into human terms. 1 nanosecond → 1 second
// block for 3 days
// block for 5 years

Futures asynchronously notify
consumers
Future[T]
A monad that handles
exceptions and latency
import scala.concurrent._
import scala.concurrent.ExecutionContext.Implicits.global
trait Future[T] {
def onComplete(callback: Try[T] Unit)⇒
(implicit executor: ExecutionContext): Unit
}

Futures asynchronously notify
consumers
import scala.concurrent._
trait Future[T] {
def onComplete(callback: Try[T] Unit)⇒
(implicit executor: ExecutionContext): Unit
}
trait Socket {
def readFromMemory(): Future[Array[Byte]]
def sendToEurope(packet: Array[Byte]): Future[Array[Byte]]
}

Sendpackets using futures
val packet: Future[Array[Byte]] =
socket.readFromMemory()
packet onComplete {
case Success(p) {⇒
val confirmation: Future[Array[Byte]] =
socket.sendToEurope(p)
}
case Failure(t) => …
}

Creating Futures
// Starts an asynchronous computation
// and returns a future object to which you
// can subscribe to be notified when the
// future completes
object Future {
def apply(body: T)⇒
(implicit context: ExecutionContext): Future[T]
}

Creating Futures
import scala.concurrent.ExecutionContext.Implicits.global
import akka.serializer._
val memory = Queue[EMailMessage](
EMailMessage(from = “Erik”, to = “Roland”),
EMailMessage(from = “Martin”, to = “Erik”),
EMailMessage(from = “Roland”, to = “Martin”))
def readFromMemory(): Future[Array[Byte]] = Future {
val email = queue.dequeue()
val serializer = serialization.findSerializerFor(email)
serializer.toBinary(email)
}

Some Other Useful Monads
● The List monad makes nondeterminism explicit in the type
system, while hiding the boilerplate of nested for-loops.
● The Promise monad makes asynchronous computation
explicit in the type system, while hiding the boilerplate of
threading logic
● The Transaction monad (non-standard) makes
transactionality explicit in the type system, while hiding the
boilerplate of invoking rollbacks
● … and more. Use monads wherever possible to keep your
code clean!

Future[T] and Try[T] are dual
trait Future[T] {
def OnComplete[U](func: Try[T] U)⇒
(implicit ex: ExecutionContext): Unit
}
Lets simplify:
(Try[T] Unit) Unit⇒ ⇒

(Try[T] Unit) Unit⇒ ⇒
Reverse:
Unit (Unit Try[T])⇒ ⇒
Simplify:
() (() Try[T])⇒ ⇒ ≈ Try[T]

Receive result of type Try[T] by passing
callback (Try[T] Unit)⇒ to method
def asynchronous(): Future[T] = { … }
Receive result of type Try[T] by blocking
until method returns
def synchronous(): Try[T] = { … }

Iterable[T]
trait Iterable[T] {
def iterator(): Iterator[T]
}
trait Iterator[T] {
def hasNext: Boolean
def next(): T
}
() (() Try[Option[T]])⇒ ⇒

Iterable[T] vs Observables[T]
() (() Try[Option[T]])⇒ ⇒
Reverse:
(Try[Option[T]] Unit) Unit⇒ ⇒
Simplify:
( T Unit⇒
, Throwable Unit⇒
, () Unit⇒
) Unit⇒

( T Unit,⇒
, Throwable Unit⇒
, () Unit⇒
) Unit⇒
trait Observable[T] {
def Subscribe(observer: Observer[T]): Subscription
}
trait Observer[T] {
def onNext(value: T): Unit
def onError(error: Throwable): Unit
def onCompleted(): Unit
}
trait Subscription {
def unsubscribe(): Unit
}

More INFO
● Functional Programming Principles in Scala
https://www.coursera.org/course/progfun
● Principles of Reactive Programming
https://www.coursera.org/course/reactive
● Programming Languages https://www.coursera.org/course/proglang
● Paradigms of Computer Programming
https://www.edx.org/course/louvainx/louvainx-louv1-01x-paradigms-compu
ter-1203
● Functional Reactive Programming & ClojureScript
https://www.youtube.com/watch?v=R4sTvHXkToQ&list=PL6JL99ajzlXU
bXUY0nwWr2imcrhJHT3Z7
● An Introduction to Functional Reactive Programming
https://www.youtube.com/watch?v=ZOCCzDNsAtI
● The reactive manifesto http://www.reactivemanifesto.org/

Scala. Introduction to FP. Monads

More Related Content

What's hot

Similar to Scala. Introduction to FP. Monads

Recently uploaded

Scala. Introduction to FP. Monads