Fp in scala part 2

FP in Scala
the exploratorium for monads (part 2)

for comprehension (review)
Use the OO/FP hybrid style List code
we can do
def test = {
val a = List(1,2)
val b = List(3,4)
for {
t1 <- a
t2 <- b
} yield ((t1,t2))
}
We get
[ (1,3) (1,4) (2,3) (2,4) ]

for comprehension (review)
It is in fact flatMap/map in disguise, it is same as
def test = {
val a = List(1,2)
val b = List(3,4)
a.flatMap {
t1 => b.map {
t2 => (t1,t2)
}
}
}
Types that has flatMap implemented is a Monadic type (You can use flatMap
to implement map)

Error Handling
This can cause ArithmeticException
def mean(xs: Seq[Double]): Double =
xs.sum / xs.length
Explicitly throw it, this is not pure (does not always return)
def mean(xs: Seq[Double]): Double =
if (xs.isEmpty)
throw new ArithmeticException("mean of empty list!")
else xs.sum / xs.length
Have default number instead of throw exception,this is pure as it return Double
all the time. But still bad for using a Double to represent empty List
def mean_1(xs: IndexedSeq[Double], onEmpty: Double): Double =
if (xs.isEmpty) onEmpty
else xs.sum / xs.length
All What else can we do?

Option/Try/Either
sealed trait Option[+A]
case object None extends Option[Nothing]
case class Some[+A](get: A) extends Option[A]
def mean_option(xs: Seq[Double]): Option[Double] =
if (xs.isEmpty) None
else Some(xs.sum / xs.length)
sealed trait Try[+T]
case class Failure[+T](exception: Throwable) extends Try[T]
case class Success[+T](value: T) extends Try[T]
def mean_try(xs: Seq[Double]): Try[Double] =
if (xs.isEmpty) Failure(new ArithmeticException("mean of
empty list!"))
else Success(xs.sum / xs.length)
sealed trait Either[+E,+A]
case class Left[+E](get: E) extends Either[E,Nothing]
case class Right[+A](get: A) extends Either[Nothing,A]
def mean_either(xs: Seq[Double]): Either[String, Double] =
if (xs.isEmpty) Left("Why gave me a empty Seq and ask me to
get mean?")
else Right(xs.sum / xs.length)
Now we return a richer type that can represent
correct value and a wrong value, Option represent
wrong value as None (Nothing), Try represent with
wrong value as Failure (Throwable), Either
represent wrong value as some type you specified.

Option/Try/Either
They all are monadic types, and have flatMap,
map and filter defined with them (Either is not a
monad, but left/right projection of Either are), so
we can use the for comprehension.
The error (the part that we do not want) will
propagate in the chain of operations. One error
means final result is error.
def test = for {
x <- mean_option(Seq(1,2,3,4,5))
y <- mean_option(Seq(4,5))
z <- mean_option(Seq())
} yield (x+y+z)
None
def test = for {
x <- mean_either(Seq(1,2,3,4,5)).left
y <- mean_either(Seq(4,5)).left
z <- mean_either(Seq()).left
} yield (x+y+z)
Right(3.0)
def test = for {
x <- mean_either(Seq(1,2,3,4,5)).right
y <- mean_either(Seq(4,5)).right
z <- mean_either(Seq()).right
} yield (x+y+z)
Left(Why gave me a empty Seq and ask me
to get mean?)
def test1 = for {
x <- mean_try(Seq(1,2,3,4,5))
y <- mean_try(Seq(4,5))
z <- mean_try(Seq())
} yield (x+y+z)
Failure(java.lang.
ArithmeticException: mean of empty
list!)

Option/Try/Either
Option, Try and Either all have much more
combinators (functions that work on the them)
give them even more tools to be useful
You can see it in the links above.

Laziness / Strictness
Generally speaking, laziness lets us separate
the description of an expression from the
evaluation of that expression.
Strictness is just link the description of an
expression and the evaluation of that
expression together.

Stream
We want to do this:
List(1,2,3,4).map(_ + 10).filter(_ % 2 == 0).map(_ * 3)
It is in fact:
List(1,2,3,4).map(_ + 10).filter(_ % 2 == 0).map(_ * 3)
List(11,12,13,14).filter(_ % 2 == 0).map(_ * 3)
List(12,14).map(_ * 3)
List(36,42)
3 passes
We can in fact use Laziness make it one pass

Examine Laziness
false && { println("!!"); true }
true || { println("!!"); false }
if (input.isEmpty) sys.error("empty input") else input
These are in fact all lazy evaluation (no prints)
We can do the same:
def if2[A](cond: Boolean, onTrue: => A, onFalse: => A): A =
if (cond) onTrue else onFalse
=> A here means lazy evaluate the passed in parameter,
by not evaluating them until they are used.
if2(false, sys.error("fail"), 3)
get 3

Examine Laziness
def maybeTwice(b: Boolean, i: => Int) = if (b) i+i else 0
val x = maybeTwice(true, { println("hi"); 1+41 })
get
hi
hi
84
the above is because lazy Param evaluated every time,we can fix it by using
this:
def maybeTwice2(b: Boolean, i: => Int) = {
lazy val j = i
if (b) j+j else 0
}
val x = maybeTwice2(true, { println("hi"); 1+41 })
get
hi
84
Because lazy val will cache the value

Stream (Lazy List)
sealed abstract class Stream[+A]
object Empty extends Stream[Nothing]
sealed abstract class Cons[+A] extends Stream[A]
def empty[A]: Stream[A] = Empty // A "smart constructor" for creating an empty stream of a particular type.
def cons[A](hd: => A, tl: => Stream[A]): Stream[A] = new Cons[A] { // A "smart constructor" for creating a nonempty stream.
lazy val head = hd // The head and tail are implemented by lazy vals.
lazy val tail = tl
}
By carefully using lazy val and => in parameter list, we can
achieve the lazy List: Stream, whose data member will not
be evaluated before get used.

Stream
Stream(1,2,3,4).map(_ + 10).filter(_ % 2 == 0).map(_ * 3)
It is in fact:
Stream(1,2,3,4).map(_ + 10).filter(_ % 2 == 0).map(_ * 3)
cons(11,Stream(2,3,4).map(_ + 10)).filter(_ % 2 == 0).map(_ * 3)
Stream(2,3,4).map(_ + 10).filter(_ % 2 == 0).map(_ * 3)
cons(12,Stream(3,4).map(_ + 10)).filter(_ % 2 == 0).map(_ * 3)
cons(12,Stream(3,4).map(_ + 10).filter(_ % 2 == 0)).map(_ * 3)
cons(36,Stream(3,4).map(_ + 10).filter(_ % 2 == 0).map(_ * 3))
cons(36,cons(13, Stream(4).map(_ + 10)).filter(_ % 2 == 0).map(_ * 3))
….
cons(36,cons(42, Empty)
Stream(36,42)
1 pass

Stream
def unfold[A, S](z: S)(f: S => Option[(A, S)]): Stream[A] =
f(z) match {
case Some((h,s)) => cons(h, unfold(s)(f))
case None => empty
}
unfold is a generic powerful
combinator to generate infinite
Stream.
val fibsViaUnfold: Stream[Int] = cons(0,
unfold((0,1)) { case (f0,f1) => Some((f1,(f1,f0+f1))) })
def test6 = fibsViaUnfold.take(5).toList
get
List(0, 1, 1, 2, 3)
Stream is also a monadic type like
List, and can use for comprehension:
def test = {
val a = Stream(1,2)
val b = Stream(3,4)
for {
t1 <- a
t2 <- b
} yield ((t1,t2))
}
get
Stream((1,3), ?)
? means it is lazy evaluated, you need
to use toList/foreach to get the real
value

Future
trait Future[+T]
when complete return a Try[T]
trait Promise[T]
It wraps in a future result of type T which can be a Failure
It is closely related to Promise, Promise is one way to
generate a Future. Promise generate a Future and later
fulfill it.

Future/Promise
val p = promise[Int]
val f = p.future
def producer = {
println("Begin producer")
Thread.sleep(3000)
val r = 100 //produce an Int
p success r
println("end producer")
}
def consumer = {
println("Begin consumer")
f onSuccess {
case r => println("receive product: " + r.toString)
}
println("end consumer")
}
def test2 = {
consumer
producer
}
get result as:
Begin consumer
end consumer
Begin producer
(after 3 secs)
end producer
receive product: 100

Future
Future is also a monadic type, you can in fact do for
comprehension on Futures.
Basically, it will give you the ability to specify how to use
the data inside the futures before it really have a value.
If one of the value is a failure, it will automatically propagate
downstream until you want to handle it case by case.
If you have dependency between the futures (based on
parameter chain), it will automatically wait.

Future
def xFut: Future[Int] = future {
Thread.sleep(10000);
println("x happened");
10
}.flatMap(i => Future.successful(i + 1))
def yFut(a: Int) : Future[Int] = future {
println("y begin")
Thread.sleep(6000);
println("y happened " + a);
20
}
def zFut(a: Int): Future[Int] = future {
println("z begin")
Thread.sleep(5000);
println("z hapenned " + a);
30
}
result is:
(after 10 secs) x happened
(immediately after) y begin
(immediately after) z begin
(after 5 secs) z hapenned 11
(after 1 secs) y happened 11
(after 4 secs)
The end
def test = {
val xf = xFut
val result: Future[(Int, (Int, Int))] =
for {
x <- xf
a <- af(x)
} yield (x, a)
Thread.sleep(20000)
println("nThe end")
}
def af: Int => Future[(Int, Int)] = a =>
{
val yf = yFut(a)
val zf = zFut(a)
for {
y <- yf
z <- zf
} yield ((y,z))
}

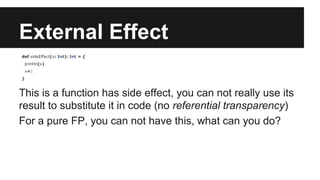
External Effect
def sideEffect(x: Int): Int = {
println(x)
x+1
}
This is a function has side effect, you can not really use its
result to substitute it in code (no referential transparency)
For a pure FP, you can not have this, what can you do?

IO monad
wrap in the IO side effect and
produces description of the IO
effect (without executing), and
then at the end, let some
interpreter do the job based on
the description.
So you have a pure core, and a
non pure shell for you program.
trait IO[+A] {
self =>
def run: A
def map[B](f: A => B): IO[B] =
new IO[B] { def run = f(self.run) }
def flatMap[B](f: A => IO[B]): IO[B] =
new IO[B] { def run = f(self.run).run }
}
object IO {
def unit[A](a: => A): IO[A] = new IO[A] { def run = a }
def flatMap[A,B](fa: IO[A])(f: A => IO[B]) = fa flatMap f
def apply[A](a: => A): IO[A] = unit(a)
}

IO monad in action
def ReadLine: IO[String] = IO { readLine }
def PrintLine(msg: String): IO[Unit] = IO { println(msg) }
def fahrenheitToCelsius(f: Double): Double =
(f - 32) * 5.0/9.0
def converter: IO[Unit] = for {
_ <- PrintLine("Enter a temperature in degrees fahrenheit: ")
d <- ReadLine.map(_.toDouble)
_ <- PrintLine(fahrenheitToCelsius(d).toString)
} yield ()
get
IO[Unit] = IO$$anon$2@2a9d61bf
converter.run
This will really run it.

IO monad
Can be expanded to aggregate different
source, distribute to different destination
Can even expanded to Future like async
operation.

Internal state
def rollDie: Int = {
val rng = new scala.util.Random
rng.nextInt(6)
}
This is not pure (can return different value based on same
input), and this is wrong (return 0 to 5), and hard to test
(correct 5 out of 6 times)
For a pure FP, you can not have this, what can you do?

State monad
sealed trait State[S,A] { self =>
def run(s: S): (A,S)
def map[B](f: A => B): State[S,B] = new State[S,B] {
def run(s: S) = {
val (a, s1) = self.run(s)
(f(a), s1)
}
}
def flatMap[B](f: A => State[S,B]): State[S,B] = new
State[S,B] {
def run(s: S) = {
val (a, s1) = self.run(s)
f(a).run(s1)
}
}
}
object State {
def apply[S,A](f: S => (A,S) ) = {
new State[S,A] {
def run(s: S): (A,S) = f(s)
}
}
def unit[S, A](a: A): State[S, A] =
State(s => (a, s))
def get[S]: State[S, S] = State(s => (s, s))
def set[S](s: S): State[S, Unit] = State(_ => ((), s))
def modify[S](f: S => S): State[S, Unit] = for {
s <- get
_ <- set(f(s))
} yield ()
}

State monad
basically, we wrap in the internal state S,
transition take a state, produce a output and a
new state.
It will not run until you ask it run with a state. So
it like IO monad, provide a description of the
transition flow and delay the execution. Before
execution, you can combine it in any way.

State monad in action
trait RNG {
def nextInt: (Int, RNG)
}
case class Simple(seed: Long) extends RNG{
def nextInt: (Int, RNG) = {
val newSeed = (seed * 0x5DEECE66DL + 0xBL) & 0xFFFFFFFFFFFFL
val nextRNG = Simple(newSeed)
val n = (newSeed >>> 16).toInt
(n, nextRNG)
}
}
type Rand[A] = State[RNG, A]
val int: Rand[Int] = State(_.nextInt)
generate new random generators:
val posInt = int.map[Int]{ i:Int => if (i < 0) -(i + 1) else i }
def positiveLessThan(n: Int): Rand[Int] = posInt.flatMap {
i => {
val mod = i % n
if (i + (n-1) - mod > 0) State.unit(mod) else positiveLessThan(n)
}}
positiveLessThan(6).run(Simple(5))
produce: 0 (now we can test it)
chain of state transitions: produce 3 result from one initial state
def test4 =
for {
x <- int
y <- int
z <- posInt
} yield ((x , y , z))
test4.run(Simple(1)) produce ((384748,-1151252339,549383846),
Simple(245470556921330))

State monad
State monad can in fact be expanded to accept
an input for transition, (A, S) => (B, S), a
powerful State Machine
State monad can also be expanded so that we
can use the Scala static type system to check if
any internal variable leaked outside (we can
have local variable, but still immutable from
outside)

for unit and flatMap
Just to remind that although we used for comprehension for all examples, for comprehension is in fact
just syntax sugar for unit/flatMap in Scala
for {
r1 <- m1
r2 <- m2
…….
rx <- mx
} yield (f(r1, r2, ….., rx))
is always the translated by compiler to
m1.flatMap {
r1 => m2.flatMap {
r2 => m3.flatMap {
……..
r x-1 => mx.flatMap {
rx => unit(f(r1, r2, ….., rx))
}
……..
}

Monad
All the types we introduced in this session are all monadic
types.
So what is a monad:
● an abstract construction in Category Theory
● an abstract structure of can do a sequence of chained
operations in FP
● a higher kinded types (type of types) in Scala
Let us see the formal definition

Monad
// id function:
// def id[A](a: A): A = a
// compose function:
// def compose[A,B,C](f: B => C, g: A => B): A => C =
// a => f(g(a))
trait Functor[F[_]] {
def map[A,B](fa: F[A])(f: A => B): F[B]
}
// Functor Law
// identity: map(x)(id) == x
// composition: map(a)(compose(f, g)) == map(map(a,g), f)
trait Monad[F[_]] extends Functor[F] {
def unit[A](a: => A): F[A]
def flatMap[A,B](ma: F[A])(f: A => F[B]): F[B]
override def map[A,B](ma: F[A])(f: A => B): F[B] =
flatMap(ma)(a => unit(f(a)))
}
// Monad Law
// left identity: f(a) == flatmap(unit(a), f)
// right identity: a == flatMap(a, x => unit(x))
// associativity: flatMap(a, x => flatMap(f(x), g)) == flatMap(flatMap(a, f), g)

Higher Kinded Type
[F[ _ ]] is called Higher Kinded Type in Scala, basically a type of types.
Compare to normal [A], this basically says we have a type F that will be used in
code, and F itself is a type that can use F[A], where A is a value type.
Use the value constructor to make a comparison:
proper first-order higher-order
value 10 (x: Int) => x (f(Int => Int)) => f(10)
type String List Monad

Monad Laws
As a formal definition of a structure, Monad is
basically a group of types that can implement
unit/flatMap function that match the signature in
the previous slide.
But that is not enough, we also have law that
Monad type need to fulfill so that we know our
implementation of unit/flatMap is correct.

Monad Laws
// Monad Law
// left identity: f(a) == flatmap(unit(a), f)
// right identity: a == flatMap(a, x => unit(x))
// associativity: flatMap(a, x => flatMap(f(x), g)) == flatMap(flatMap(a, f), g)
As the name suggest, associative law means flatMap
operation obey the associative law similar to plus/multiple
(a+b) + c = a + (b+c)
As the name suggest, identity laws basically means we
have a unit function that server as a identity in monad, like
0 in addition, which similar to x + 0 = x, and 0 + x = x

Still, what is a Monad
Now see all these formal definition, still what is a Monad for us programmer? and Why we need them?
def unit[A](a: => A): M[A]
def flatMap[A,B](ma: M[A])(f: A => M[B]): M[B]
A bit long explanation here:
Monad seems just like a wrapper, it wraps in a basic type (A here), and put into a context M, generate
a richer type (M[A] here). unit function does this.
We care about the value of type A in context M, but we hate part of the context that is troublesome.
The troublesome part in the context M make us lose the composability for values of type A in
context M (make us not be able to combine functions generate value of type A). So we wrap in the
value and troublesome part together into context M, and now we can combine functions that generate
M[A], just as if the troublesome part is gone. That is what flatMap does.
Using unit and flatMap, we regain the composability for values of type A in context M, which is
kind of what monad brings us, and it specifically useful in pure FP as side effect are the things prevent
clean combination of functions.

Example monads in our talk
Context Troublesome Part
List multiple value
Option can have empty value
Try can have error
Either can be another unintended (error message etc.) value
Stream multiple value and also not accessible until touched
Future can have error and also have latency to be availuable
IO input/output side effect
State internal states side effect

Fp in scala part 2

More Related Content

What's hot

Similar to Fp in scala part 2

Recently uploaded

Fp in scala part 2