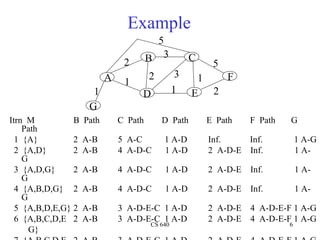
The document summarizes routing and switching fabrics. It discusses link state routing, Dijkstra's shortest path algorithm, and link state routing protocols. It also covers goals in switch design such as throughput, size, cost, and functionality. Different switching fabric designs are mentioned for forwarding data from input ports to output ports in switches.

1. Routing and Switching Fabrics Outline Link state routing Link weights Switching Fabrics

2. Intradomain Routing Summary Intradomain routing protocols determine how forwarding tables are maintained in routers Least cost algorithms Distance vector routing Algorithm based on building forwarding table by distributing vector of distances to neighbors Completely distributed and based only on knowledge of immediate neighbors Known to converge under static conditions Count to infinity problem Limited network diameter

3. Link State (Dijkstra’s algorithm,OSPF) Find SP from a given node by sending path data to all nodes and developing paths in order of increasing length Strategy Route calculation is based on sum of all accumulated link state information All nodes forward all information to all directly connected links Link State Packet (LSP) – created by each node id of the node that created the LSP cost of the link to each directly connected neighbor sequence number (SEQNO) time-to-live (TTL) for this packet

4. Link State contd. Send out LSP based on timer and triggers Timer should be coarse grained Seqno’s do not wrap around Since when routers reboot – they start at seqno 0 64 bit field Routing table is not computed until LSP’s from all nodes have been received

5. Route Calculation Dijkstra’s shortest path algorithm Let N denotes set of nodes in the graph l ( i , j ) denotes non-negative cost (weight) for edge ( i , j ) s denotes this node M denotes the set of nodes incorporated so far C ( n ) denotes cost of the path from s to node n M = { s } for each n in N - { s } C ( n ) = l ( s , n ) /* Costs of directly connected nodes */ while ( N != M ) M = M union { w } such that C ( w ) /* Add a node */ is the minimum for all w in ( N - M ) for each n in ( N - M ) /* Recalculate costs */ C ( n ) = MIN( C ( n ), C ( w ) + l ( w, n ))

6. Example Itrn M B Path C Path D Path E Path F Path G Path 1 {A} 2 A-B 5 A-C 1 A-D Inf. Inf. 1 A-G 2 {A,D} 2 A-B 4 A-D-C 1 A-D 2 A-D-E Inf. 1 A-G 3 {A,D,G} 2 A-B 4 A-D-C 1 A-D 2 A-D-E Inf. 1 A-G 4 {A,B,D,G} 2 A-B 4 A-D-C 1 A-D 2 A-D-E Inf. 1 A-G 5 {A,B,D,E,G} 2 A-B 3 A-D-E-C 1 A-D 2 A-D-E 4 A-D-E-F 1 A-G 6 {A,B,C,D,E 2 A-B 3 A-D-E-C 1 A-D 2 A-D-E 4 A-D-E-F 1 A-G G} 7 {A,B,C,D,E 2 A-B 3 A-D-E-C 1 A-D 2 A-D-E 4 A-D-E-F 1 A-G F,G} D G A B C E F 5 1 1 1 2 1 3 5 2 2 3

7. Link State Routing Summary One of the oldest algorithm for routing Finds SP by developing paths in order of increasing length Requires each node to have complete information about the network Nodes exchange information with all other nodes in the network Known to converge quickly under static conditions Does not generate much network traffic Other possible routing algorithms?

8. Metrics for link cost Simplest method is to simply assign 1 to each link Original ARPANET metric link cost = number of packets enqueued on each link This moves packets toward shortest queue not the destination!! took neither latency or bandwidth into consideration New ARPANET metric link cost = average delay over some time period stamp each incoming packet with its arrival time ( AT ) record departure time ( DT ) when link-level ACK arrives, compute Delay = (DT - AT) + Transmit + Latency Transmit and latency are static for the link if timeout, reset DT to departure time for retransmission Fine Tuning compress range over which costs can span using static function smooth variation of cost over time using averaging

9. Introduction to switching fabrics Switches must not only determine routing but also do forwarding quickly and efficiently If this is done on a general purpose computer, the I/O bus limits performance This means that a system with 1Gbps I/O could not handle OC12 Special purpose hardware is required Switch capabilities drive protocol decisions Context – a “router” is defined as a datagram “switch” Switching fabrics are internal to routers and facilitate forwarding

10. Goals in switch design Throughput Ability to forward as many pkts per second as possible Size Number of input/output ports Cost Minimum cost per port Functionality QoS

11. Throughput Consider a switch with n inputs and m outputs and link speed of s n Typical notion of throughput:  s n This is an upper bound Assumes all inputs get mapped to a unique output Another notion of throughput is packets per second (pps) Indicates how well switch handles fixed overhead operations Throughput depends on traffic model Goal is to be representative This is VERY tricky!

12. Size/Scalability/Cost Maximum size is typically limited by HW constraints Eg. fanout Cost is related to number of inputs/outputs How does cost scale with inputs/outputs?

13. Ports and Fabrics Ports on switches handle the difficult functions of signaling, buffering, circuits, RED, etc. Most buffering is via FIFO on output ports This prevents head-of-the-line blocking on input ports which is possible if only one input port can forward to one output port at a time Switching fabrics in switches handle the simple function of forwarding data from input ports to output ports Typically fabric does not buffer (but it can) Contention is an issue Many different designs