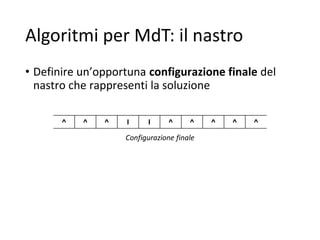
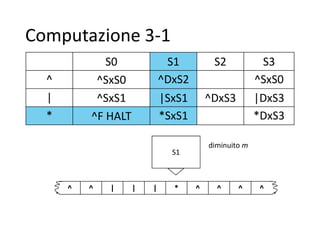
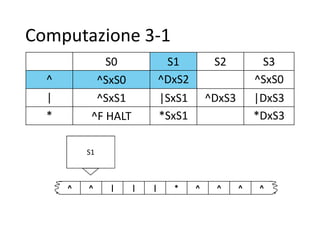
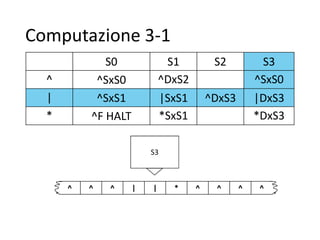
Il documento descrive la macchina di Turing, un modello astratto di calcolo introdotto da Alan Turing nel 1936, utilizzato per fornire una definizione formale di algoritmo e affrontare problemi di decisione. Viene illustrata la struttura e il funzionamento della macchina, compresi il nastro, la testina di lettura/scrittura e l'unità di controllo, con esempi pratici di algoritmi per operazioni aritmetiche come la sottrazione. Inoltre, si discute la tesi di Church-Turing, evidenziando che le funzioni calcolabili da una macchina di Turing coincidono con quelle calcolabili da altri formalismi, come i linguaggi di programmazione moderni.

1. La macchina più geek
dell’universo
The Turing Machine
Pierpaolo Basile

2. Macchina di Turing
• Modello astratto di
calcolo introdotto nel
1936 da Alan Turing
• Fornire una definizione
matematica/formale
del concetto di
algoritmo
• Risolvere il problema di
decisione

3. Algoritmo
«Procedimento di risoluzione dei problemi
per passi successivi, in particolare un
procedimento computazionale ricorsivo
determinato per risolvere un problema in
un numero finito di passi»
American Heritage Dictionary

4. Problema di decisione
«Esiste un «processo
meccanico» in grado di
stabilire se per un dato
problema esiste un
algoritmo risolvibile in
un numero finito di
passi?»

5. La Macchina di Turing (MdT)

6. Problema di decisione

7. Problema di decisione
• Costruiamo un algoritmo H che prende in input un
altro algoritmo P
• H si comporta nel seguente modo:
vero se P termina
falso se P NON termina
H restituisce

8. Problema di decisione
• Costruiamo un altro algoritmo K che utilizzando H
decide se P termina
stampa loop se H(P)=falso
va in loop se H(P)=vero
K restituisce
K si comporta in maniera opposta al suo input P!

9. Problema di decisione
• Supponiamo di dare in input a K lo stesso K
stampa loop se K NON
termina
va in loop se K termina
K(K) restituisce
Assurdo
• K(K) si ferma quando K va in loop
• K(K) va in loop quando K si ferma
H non può esistere

10. La Macchina di Turing

11. MdT: il nastro
• Nastro potenzialmente infinito diviso in celle
(memoria)
• ogni cella contiene un simbolo preso da un
alfabeto finito

12. MdT: la testina…
• Testina di lettura/scrittura
• può leggere/scrivere in una cella per volta

13. MdT: …la testina…
• Testina di lettura/scrittura
• può leggere/scrivere in una cella per volta
• può spostarsi a destra o a sinistra di una cella
per volta

14. MdT: …la testina
• Testina di lettura/scrittura
• può leggere/scrivere in una cella per volta
• può spostarsi a destra o a sinistra di una cella
per volta

15. MdT: l’unità di controllo
• Unità di controllo
• decodifica ed esegue comandi rivolti alla testina
(controlla la testina)
Unità di
Controllo

16. MdT: lo stato
• La macchina può trovarsi in un numero finito di
stati
• La macchina può cambiare stato in seguito ad una
lettura di un simbolo dal nastro
• Chiameremo configurazione la coppia:
<simbolo visibile alla testina, stato
corrente>
• Esiste uno stato «speciale» HALT che indica la fine
dell’algoritmo

17. Macchine di Turing (MdT)
L’unità di controllo esegue un algoritmo A sui dati
memorizzati sul nastro
Le istruzioni di A sono del tipo:
< simbolo_letto,
stato_corrente,
simbolo_da_scrivere,
sinistra/destra/ferma,
nuovo_stato >
configurazione

18. Algoritmi per MdT: il nastro
• Definire un’opportuna configurazione iniziale del
nastro
• Codificare i dati
• Es.: nastro iniziale per problema della sottrazione tra
interi
4 – 2
operandi codificati con ‘I’ e separati da *
blank=^
^ I I I I * I I ^ ^
Configurazione iniziale

19. Algoritmi per MdT: il nastro
• Definire un’opportuna configurazione finale del
nastro che rappresenti la soluzione
^ ^ ^ I I ^ ^ ^ ^ ^
Configurazione finale

20. Algoritmi per MdT: il controllo
• Definire le azioni (algoritmo) dell’unità di controllo
• In pratica l’algoritmo per una MdT è una sequenza
di quintuple del tipo:
< simbolo_letto, stato_corrente, simbolo_da_scrivere,
sinistra/destra/ferma, nuovo_stato >
Es.
<|, S1, ^, D, S2 > : se leggi | e sei nello stato S1 allora
scrivi ^, sposta a destra la testina e vai nello stato S2

21. MdT: sottrazione tra interi
• Progettiamo un algoritmo per eseguire la
sottrazione tra due numeri interi n e m, n≥0, m≥0
• Per semplicità assumiamo che n≥m
• La testina è posizionata sulla prima cella vuota a destra
dell’ultimo simbolo del sottraendo
• Il modello di calcolo ci "obbliga" a pensare l’algoritmo in
base alle operazioni possibili
S0
Configurazione iniziale

22. MdT: sottrazione tra interi
• Progettiamo un algoritmo per eseguire la
sottrazione tra due numeri interi n e m, n≥0, m≥0
• Per semplicità assumiamo che n≥m
• La testina è posizionata sulla prima cella vuota a destra
dell’ultimo simbolo del sottraendo
• Il modello di calcolo ci "obbliga" a pensare l’algoritmo in
base alle operazioni possibili
S0
Configurazione iniziale
Cancellare ugual numero di
simboli da n e da m in
modo che sul nastro resti
solo il risultato finale

23. MdT: algoritmo per la sottrazione
1. Diminuisci di una unità m
• ricorda di aver cancellato un simbolo da m
2. Spostati a Sx in cerca del primo simbolo di n
3. Cancellalo
• Ricorda che ora entrambi gli operandi sono stati
diminuiti di una unità
4. Spostati a Dx in cerca dell’ultimo simbolo di m
• Se non ci sono più simboli da cancellare da m allora
cancella il separatore  HALT
• In caso contrario torna al punto 1

24. La MdT per la sottrazione…
• Alfabeto = {I, *, ^}
• Stati = {S0, S1, S2, S3, HALT}
• S0 ≡ stato iniziale della computazione ovvero
ricerca ultimo simbolo di m
• S1 ≡ diminuito m
• S2 ≡ raggiunto simbolo iniziale di n
• S3 ≡ diminuiti entrambi operandi

25. …la MdT per la sottrazione
<^,S0,^,Sx,S0>
<|,S0,^,Sx,S1>
<*,S0,^,F,HALT>
<^,S1,^,Dx,S2>
<|,S1,|,Sx,S1>
<*,S1,*,Sx,S1>
<|,S2,^,Dx,S3>
<^,S3,^,Sx,S0>
<|,S3,|,Dx,S3>
<*,S3,*,Dx,S3>

26. La Matrice Funzionale
S0 S1 S2 S3
^ ^SxS0 ^DxS2 ^SxS0
| ^SxS1 |SxS1 ^DxS3 |DxS3
* ^FHALT *SxS1 *DxS3

27. Computazione 3-1
S0
^ ^ | | | * | ^ ^ ^
n m
S0 S1 S2 S3
^ ^SxS0 ^DxS2 ^SxS0
| ^SxS1 |SxS1 ^DxS3 |DxS3
* ^F HALT *SxS1 *DxS3

28. Computazione 3-1
S0
^ ^ | | | * | ^ ^ ^
S0 S1 S2 S3
^ ^SxS0 ^DxS2 ^SxS0
| ^SxS1 |SxS1 ^DxS3 |DxS3
* ^F HALT *SxS1 *DxS3

29. Computazione 3-1
S0
^ ^ | | | * | ^ ^ ^
S0 S1 S2 S3
^ ^SxS0 ^DxS2 ^SxS0
| ^SxS1 |SxS1 ^DxS3 |DxS3
* ^F HALT *SxS1 *DxS3

30. Computazione 3-1
S1
^ ^ | | | * ^ ^ ^ ^
diminuito m
S0 S1 S2 S3
^ ^SxS0 ^DxS2 ^SxS0
| ^SxS1 |SxS1 ^DxS3 |DxS3
* ^F HALT *SxS1 *DxS3

31. Computazione 3-1
S1
^ ^ | | | * ^ ^ ^ ^
S0 S1 S2 S3
^ ^SxS0 ^DxS2 ^SxS0
| ^SxS1 |SxS1 ^DxS3 |DxS3
* ^F HALT *SxS1 *DxS3

32. Computazione 3-1
S1
^ ^ | | | * ^ ^ ^ ^
S0 S1 S2 S3
^ ^SxS0 ^DxS2 ^SxS0
| ^SxS1 |SxS1 ^DxS3 |DxS3
* ^F HALT *SxS1 *DxS3

33. Computazione 3-1
S1
^ ^ | | | * ^ ^ ^ ^
S0 S1 S2 S3
^ ^SxS0 ^DxS2 ^SxS0
| ^SxS1 |SxS1 ^DxS3 |DxS3
* ^F HALT *SxS1 *DxS3

34. Computazione 3-1
S1
^ ^ | | | * ^ ^ ^ ^
S0 S1 S2 S3
^ ^SxS0 ^DxS2 ^SxS0
| ^SxS1 |SxS1 ^DxS3 |DxS3
* ^F HALT *SxS1 *DxS3

35. Computazione 3-1
S2
^ ^ | | | * ^ ^ ^ ^
raggiunto simbolo
iniziale di n
S0 S1 S2 S3
^ ^SxS0 ^DxS2 ^SxS0
| ^SxS1 |SxS1 ^DxS3 |DxS3
* ^F HALT *SxS1 *DxS3

36. Computazione 3-1
S3
^ ^ ^ | | * ^ ^ ^ ^
Diminuiti entrambi
gli operandi
S0 S1 S2 S3
^ ^SxS0 ^DxS2 ^SxS0
| ^SxS1 |SxS1 ^DxS3 |DxS3
* ^F HALT *SxS1 *DxS3

37. Computazione 3-1
S3
^ ^ ^ | | * ^ ^ ^ ^
S0 S1 S2 S3
^ ^SxS0 ^DxS2 ^SxS0
| ^SxS1 |SxS1 ^DxS3 |DxS3
* ^F HALT *SxS1 *DxS3

38. Computazione 3-1
S3
^ ^ ^ | | * ^ ^ ^ ^
S0 S1 S2 S3
^ ^SxS0 ^DxS2 ^SxS0
| ^SxS1 |SxS1 ^DxS3 |DxS3
* ^F HALT *SxS1 *DxS3

39. Computazione 3-1
S3
^ ^ ^ | | * ^ ^ ^ ^
S0 S1 S2 S3
^ ^SxS0 ^DxS2 ^SxS0
| ^SxS1 |SxS1 ^DxS3 |DxS3
* ^F HALT *SxS1 *DxS3

40. Computazione 3-1
S0
^ ^ ^ | | * ^ ^ ^ ^
Stato iniziale della
computazione
S0 S1 S2 S3
^ ^SxS0 ^DxS2 ^SxS0
| ^SxS1 |SxS1 ^DxS3 |DxS3
* ^F HALT *SxS1 *DxS3

41. Computazione 3-1
HALT
^ ^ ^ | | ^ ^ ^ ^ ^
trovare un * nello stato iniziale
della computazione è segno del
fatto che non ci sono più simboli
da processare in m
S0 S1 S2 S3
^ ^SxS0 ^DxS2 ^SxS0
| ^SxS1 |SxS1 ^DxS3 |DxS3
* ^F HALT *SxS1 *DxS3

42. Have Fun with MdT
1. Stabilire se un numero rappresentato con ‘|’ è pari oppure
dispari
2. Stabilire se una stringa binaria è palindroma (ovvero si legge
indifferentemente da Sx a Dx, es.: 010010)

43. Soluzioni

44. Esercizio 1
• Stabilire se un numero rappresentato con ‘|’ è pari
oppure dispari
S0
^ ^ ^ | | | | ^ ^ ^
Configurazione iniziale
^ ^ ^ ^ ^ ^ ^ P ^ ^
Configurazione finale

45. Esercizio 1
• Cancellare i simboli dal nastro e memorizzare in
uno stato la situazione di parità/disparità
• q0 ≡ stato iniziale della computazione ovvero PARI
• q1 ≡ DISPARI
S0 S1
^ P F HALT D F HALT
| ^ Dx S1 ^ Dx S0

46. Esercizio 2
• Stabilire se una stringa binaria è palindroma
(ovvero si legge indifferentemente da Sx a Dx, es.:
010010)
S0
^ ^ ^ 0 1 1 0 ^ ^ ^
Configurazione iniziale
^ ^ ^ ^ ^ ^ ^ ^ ^ ^
Configurazione finale

47. Esercizio 2
• Stabilire se una stringa binaria è palindroma
(ovvero si legge indifferentemente da Sx a Dx, es.:
010010)
S0
^ ^ ^ 0 1 0 0 ^ ^ ^
Configurazione iniziale
^ ^ ^ ^ 1 ^ ^ ^ ^ ^
Configurazione finale

48. Esercizio 2
S0 S1 S2 S3 S4 S5
0 0 S0 Dx ^ S2 Sx 0 S2 Sx 0 S3 Sx ^ S0 Dx 0 F Halt
1 1 S0 Dx ^ S3 Sx 1 S2 Sx 1 S3 Sx 1 F Halt ^ S0 Dx
^ ^ S1 Sx ^ S5 Dx ^ S4 Dx ^ S5 Dx ^ F Halt ^ F Halt
S1: leggo il primo simbolo a sinistra
S2: ho letto 0 e mi sposto tutto a sinistra
S3: ho letto 1 e mi sposto tutto a sinistra
S4: verifica che l’ultimo simbolo a sinistra sia 0
S5: verifica che l’ultimo simbolo a sinistra sia 1
S0: mi riporto a destra della stringa se leggo 0 o 1, altrimenti prova
a leggere il primo simbolo a sinistra

49. Tesi di Church-Turing
• La classe delle funzioni calcolabili coincide con la
classe delle funzioni calcolabili da una MdT
• ogni funzione calcolabile è calcolata da una MdT
• non esiste alcun formalismo capace di risolvere una
classe di problemi più ampia di quella che si può
risolvere con MdT
• Le funzioni calcolabili con C o Java sono di più di
quelle calcolabili con MdT?

50. Tesi di Church-Turing
• La classe delle funzioni calcolabili coincide con la
classe delle funzioni calcolabili da una MdT
• ogni funzione calcolabile è calcolata da una MdT
• non esiste alcun formalismo capace di risolvere una
classe di problemi più ampia di quella che si può
risolvere con MdT
• Le funzioni calcolabili con C o Java sono di più di
quelle calcolabili con MdT?
NO

51. MdT vs. CPU
• MdT
1. Legge / scrive su
nastro
2. Transita in un nuovo
stato
3. Si sosta sul nastro di
cella in cella
4. Esegue un programma
specifico CABLATO
nella macchina  è
specifica per un certo
problema
• CPU
1. lettura / scrittura da /
su memoria RAM o
ROM
2. nuova configurazione
dei registri della CPU
3. scelta della cella di
memoria su cui
operare
4. È generale, nel senso
che può eseguire
programmi diversi

52. La MdT Universale (MdTU)
• Legge dal nastro DATI e PROGRAMMA
• Il programma non è più cablato nell’unità di controllo
• Codificato sul nastro come i dati
• In pratica sono rappresentate sul nastro anche le 5-ple
che definiscono l’algoritmo solutivo
• E’ una macchina programmabile
• prende le 5-ple (istruzioni) dal nastro  FETCH
• le decodifica  DECODE
• le esegue scrivendo sul nastro  EXECUTE
• E’ un computer programmabile!

53. MdTU vs. Macchina Von Neumann
MdTU
(controllo)
Nastro
MdTU è un modello della macchina di Von Neumann
ovvero un modello degli attuali calcolatori!
(manca solo la parte di I/O)
processore
memoria
interna
memoria
esterna
interfaccia
periferiche

54. La MdT di LEGO
• Realizzata interamente con mattoncini Lego
utilizzando il LEGO MINDSTORMS NXT set
http://www.legoturingmachine.org/

55. La MdT di LEGO

56. pierpaolo.basile@gmail.com

57. BACKUP SLIDES

58. MdT: il modello matematico
Una MdT è definita da una quintupla
M = (X, Q, fm, fd, )
X = insieme finito di simboli
 comprende il blank ovvero cella vuota
Q = insieme finito di stati
 comprende HALT che definisce la terminazione

59. MdT: il modello matematico
Una MdT è definita da una quintupla:
M = (X, Q, fm, fd, )
Funzione di direzione
 Determina lo spostamento della testina
 S=sinistra, D=destra, F=ferma
},,{: FDSXQfd 
XXQfm :Funzione di macchina
 Determina il simbolo da scrivere sul nastro
Funzione di transizione di stato
 Definisce lo stato successivo della computazione
QXQ :