Il documento tratta un corso di abilità informatiche in ingegneria chimica, con focus su MATLAB come linguaggio di programmazione e ambiente di calcolo scientifico. Vengono esplorati topics tra cui l'uso di comandi, vettori, matrici, cicli, funzioni e grafici in MATLAB. Inoltre, il documento fornisce esempi pratici e spiega la creazione di script e funzioni, evidenziando l'importanza della precisione e della gestione degli errori.

1. Abilità Informatiche
Ingegneria Chimica
Lezione 23 del 9/5/2012
Prof. Antonino Stelitano

2. Docente Antonino
Stelitano
Tutor
Lezioni Lunedì 14:00 – 17:30 aula 16
Mercoledì 15:45 – 19:00 aula 17
Lab. Paolo Ercoli – via Tiburtina 205
Ricevimento: Per antonino.stelitano@uniroma1.it
appuntamento
stelitano.a@libero.it
Sito web: http://w3.uniroma1.it/ab_informatiche

3. Introduzione a Matlab

4. Che cosa è Matlab
Matlab è
• un linguaggio di programmazione
• un ambiente di calcolo scientifico con routines
altamente specializzate
• un ambiente grafico

5. Argomenti trattati
• Matlab come calcolatrice
• Inserire comandi, vettori, matrici
• Operazioni su vettori
• Cicli
• File .m e functions
• Grafici

6. Matlab come calcolatrice
Per usare Matlab come calcolatrice, inserisco i comandi dopo il >>.
Per esempio:
>> 2+1 >> log(4)
ans = Oppure: ans =
3 1.3863
Matlab normalmente stampa solo le prime 4 cifre decimali,
ma in realta’ne memorizza molte di piu’. Per vederle tutte:
>> format long
>> log(4)
ans =
1.38629436111989

7. Help online
Matlab ha un ricco help online. Per accedere alle informazioni, basta
digitare help nella finestra dei comandi:
>> help
HELP topics:
matlabgeneral - General purpose commands.
matlabops - Operators and special characters.
matlablang - Programming language constructs.
matlabelmat - Elementary matrices and matrix manipulation.
matlabelfun - Elementary math functions.
matlabspecfun - Specialized math functions.
matlabmatfun - Matrix functions - numerical linear algebra.
… etc.

8. Per avere informazioni su una particolare function, per esempio,
eye:
>> help eye
EYE Identity matrix.
EYE(N) is the N-by-N identity matrix.
EYE(M,N) or EYE([M,N]) is an M-by-N matrix with 1's on
the diagonal and zeros elsewhere.
EYE(SIZE(A)) is the same size as A.
See also ONES, ZEROS, RAND, RANDN.

9. Per cercare informazioni su un particolare argomento, si usa il
comando lookfor (look for = cerca)
>> lookfor logarithm
LOGSPACE Logarithmically spaced vector.
LOG Natural logarithm.
LOG10 Common (base 10) logarithm.
LOG2 Base 2 logarithm and dissect floating point number.
BETALN Logarithm of beta function.
GAMMALN Logarithm of gamma function.
LOGM Matrix logarithm.
L’output di lookfor contiene i nomi di tutte le functions che
presentano la parola “logarithm”nel loro help.

10. Inserire comandi, vettori e matrici
Per inserire comandi, basta digitare il comando al prompt
per esempio:
>> pi
ans =
3.1416
Matlab crea una variabile ans a cui assegna il valore
richiesto (in questo caso pi greco). Anche qui:
>> format long
>> pi
ans =
3.14159265358979

11. Per inserire matrici, si usano parentesi quadre:
il comando:
>> a=[2, 3; 1, 2]
produce in output:
a=
2 3
1 2
Notare che non c’è nessun bisogno di dimensionare la matrice:
Matlab infatti attribuisce automaticamente la memoria richiesta.
Attenzione!
Matlab automaticamente stampa l’output di ogni comando: per
eliminare questa risposta è necessario terminare il comando con
un ;
Questo comando, per esempio, non produce nessun output:
>> a=[2, 3; 1, 2];

12. E’ possibile costruire matrici automaticamente:
>> a=zeros(2)
a=
0 0
0 0
crea una matrice 2 per 2 di zeri, mentre:
>> a=zeros(2,3)
a=
0 0 0
0 0 0
crea una matrice 2 per 3.
N.B. Le functions di Matlab (come zeros) possono accettare un
numero variabile di elementi in input.
Analogamente funzionano le functions ones (che genera matrici
di 1), rand (che genera matrici di numeri casuali), eye (che
genera le matrici identità).

13. Column notation
Il carattere : indica un ciclo implicito, che si usa per creare
vettori:
>> x=1:5
x=
1 2 3 4 5
Si può introdurre anche un incremento non intero:
>> x=1:.1:2
x=
Columns 1 through 8
1.0000 1.1000 1.2000 1.3000 1.4000 1.5000 1.6000 1.7000
Columns 9 through 11
1.8000 1.9000 2.0000

14. Operazioni su vettori
Matlab esegue automaticamente le operazioni algebriche sulle
matrici:
>> a=ones(2,3);
>> b=ones(2,3);
>> a+b
ans =
2 2 2
2 2 2
o anche:
>> a=2*eye(2)
a=
2 0
0 2

15. Naturalmente, le operazioni richieste devono essere ben definite:
>> a*b
??? Error using ==> *
Inner matrix dimensions must agree.
Perché il prodotto fra matrici è definito solo quando il numero di colonne
della prima matrice e il numero di righe della seconda coincidono.
Posso invece moltiplicare a per la trasposta di b. Per calcolare la trasposta:
>> b'
ans =
ora il prodotto è ben definito:
1 1
1 1
1 1 >> a*b'
ans =
3 3
3 3

16. Si possono calcolare funzioni di matrici:
>> a=zeros(1,2)
a=
0 0
>> b=cos(a)
b=
1 1
Con questo sistema è possibile calcolare in modo vettoriale i
valori di una funzione:
>> x=1:0.1:2;
>> fx=cos(3*x)+2;

17. Per calcolare un prodotto, una potenza o un quoziente, Matlab
distingue due operatori diversi. Nel caso del prodotto per esempio:
* denota il prodotto fra due matrici
.* denota il prodotto fra le singole componenti
La stessa distinzione vale per / (quoziente) e ^ (potenza)
Esempio
>> x=1:0.1:2;
>> fx=cos(3*x)*exp(x);
??? Error using ==> *
Inner matrix dimensions must agree.
Il comando corretto è:
>> fx=cos(3*x).*exp(x);

18. Un altro esempio:
>> x=ones(2,2);
>> x^2
ans =
2 2
2 2
>> x.^2
ans =
1 1
1 1
Infatti X^2 indica il prodotto della matrice X con sé stessa,
che è definito solo per matrice quadrate, cioè X^2 = X*X,
mentre A=X.^2 indica la matrice con elementi
A i,j = ( X i,j ) 2 .

19. Operatori relazionali
Gli operatori relazionali più comuni sono:
== uguale
~= diverso da
< minore di
<= minore o uguale etc.
Esempi:
>> x=2; (questa relazione e’falsa:)
>> x==0 => ans=0
ans =
0
>> x==2 (questa relazione è vera:)
ans = => ans=1
1

20. Gli operatori relazionali possono essere applicati anche alle
matrici:
>> a=[1 2; 0 -1];
>> a>0 (qui i primi due elementi sono veri)
ans =
1 1
0 0
>> a>=0 (qui i primi tre elementi sono veri)
ans =
1 1
1 0

21. Operatori logici
Gli operatori logici più comuni sono:
& and logico
| or logico
~ not logico
Esempi:
>> x=1; y= -1;
>> x>0 & y>0 (questa relazione è falsa)
ans =
0
>> x>0 | y>0 (questa relazione è vera)
ans =
1

22. Ciclo if … elseif …end
Il ciclo basato su if ha la struttura:
if espressione
istruzioni
end
Esempio:
Le istruzioni vengono eseguite solo se
>> a=[1,4];
espressione è vera, cioè se espressione
>> if a>0
è diversa da zero.
sqrt(a)
end
>> if cos(2)
ans = Esempio:
display('ciao')
1 2
end

23. Un esempio piu’ complicato:
if x=='domenica' | x=='sabato ' In questo esempio, x deve
sempre essere impostato
display('Evviva!') come variabile di 8
elseif x=='venerdi ' caratteri
display('Torno a casa')
else
display('Vado al Dipartimento')
end
Se imposto: >> x='sabato '
ottengo: ans =
Evviva!

24. Ciclo for … end
Il ciclo for ha la struttura:
for variabile = espressione
istruzioni
end
Di solito espressione è un vettore:
>> s=0;
>> for i=1:10
s=s+i;
end calcola la somma dei primi 10 numeri
>> s interi
s=
55

25. I cicli for possono essere uno dentro l’altro:
>> n=4;
>> for i=1:n
for j=1:i
a(i,j) = 1;
end
end
Crea una matrice triangolare inferiore:
>> a
a=
1 0 0 0
1 1 0 0
1 1 1 0
1 1 1 1

26. Non sempre i cicli hanno indici interi.
Per esempio:
>> for x=[pi, 51, -72.1]
display(x)
end
in output produce questo risultato:
x=
3.14159265358979
x=
51
x=
-72.1

27. Ciclo while … end
Il ciclo while ha la seguente struttura
while espressione
istruzioni
end
Esempio
>> i=1;
>> while i<5
i=i+1;
end
>> i
i=
5

28. Calcolare la precisione di macchina
• Devo calcolare un numero x=2^p tale che
x=x+1
• .
%Calcola la precisione di macchina
p = 0;
epsilon=1;
while 1~=1+epsilon
epsilon = epsilon/2;
p = p+1;
end
epsilon=epsilon*2, p=p-1
N.B. Il ciclo viene eseguito una volta di troppo, per questo nell’ultima
riga il valore di epsilon viene corretto

29. Eseguendo il programma precedente, troviamo:
epsilon =
2.2204e-016
p=
52
Questo è lo stesso valore contenuto nella variabile intrinseca
eps, che contiene appunto la precisione di macchina:
>> eps
ans =
2.2204e-016

30. Calcolare il piu’ piccolo numero floating point
della forma x=2^p
• Devo trovare un numero della forma x=2^p
tale che x sia considerato 0.
•
% Calcola il piu' piccolo numero floating point della
% forma xmin=2^p
x=1;
while x>0
xmin = x;
x=x/2;
end
xmin

31. Risultati:
Il piu’ piccolo numero floating point è
>> xmin
xmin =
4.9407e-324
Notare che se dimezzo xmin, trovo:
>> xmin/2
ans =
0

32. Il più grande numero floating point
Il più grande numero floating point della forma 2^p è
>> xmax
xmax =
8.9885e+307
Se raddoppio xmax, trovo
>> xmax*2
ans =
Inf

33. File .m e functions
• Un file .m (M-file) è un programma riconoscibile da Matlab.
La scrittura di files .m permette di:
• Sperimentare con un algoritmo, senza dover reintrodurre
una lunga lista di comandi
• Ottenere una documentazione permanente per un lavoro
• Ottenere programmi che possono essere riutilizzati, per
esempio cambiando solo i dati
• Scambiare programmi con altri utenti

34. Struttura di un file .m
•I Script M-files: due tipi: di comandi. Non
files .m sono di
sono files
hanno variabili in entrata e in uscita e operano
sulle variabili del workspace
• function M-files: sono files di comandi, che
hanno argomenti in entrata e in uscita. Le
variabili interne a questi programmi non
influenzano le variabili del workspace

35. Commenti
• Sia gli scripts che le functions devono
contenere righe di commento.
• I commenti sono segnalati da %: Matlab
ignora tutti i caratteri di una riga dopo il %
• Le prime righe di commento di uno script o di
una function diventano parte dello help online

36. Esempio: file radice.m
% Questo file calcola la radice degli elementi di
% una matrice a, se a>0, altrimenti da' un messaggio di errore
if a>=0
a=sqrt(a)
else
display('errore')
end
Attenzione: nel workspace deve essere stata definita una
variabile a. Inoltre l’esecuzione di questo script modifica il
contenuto della variabile a

37. Function M-files
Esempio
function a=radfunz(x)
% RADFUNZ(X) calcola la radice degli elementi di X
% se X>=0, altrimenti stampa un messaggio di errore
%
if x>=0
a=sqrt(x)
else
display('errore')
end
Questo file deve essere salvato come radfunz.m

38. Struttura di una function
• La function inizia con una riga che ne specifica il
nome (nell’esempio radfunz), le variabili di input e
le variabili di output.
• La function deve essere salvata in un file con lo
stesso nome (nell’esempio radfunz.m)
• I commenti dopo la prima riga faranno parte dello
help on-line
• Seguono le istruzioni con eventuali altri commenti

39. Un altro esempio:
function [xmin,xmax]=minmax(a)
%MINMAX(A,M,N) calcola l'elemento minimo, XMIN, e l’elemento
% massimo, XMAX della matrice A.
xmin=Inf; xmax=-Inf;
% ricava le dimensioni della matrice A:
[m,n] = size(a);
for i=1:m
for j=1:n
if a(i,j) > xmax
xmax = a(i,j);
end
if a(i,j) < xmin
xmin = a(i,j);
end
end
end

40. La function precedente ha la seguente struttura
function [out1,out2,…]=funz(in1,in2,….)
• Gli argomenti in output vanno a sinistra dell’ =, fra [
]
• Gli argomenti in input vanno a destra dell’ = , fra (
)
• Posso usare un numero di argomenti minore di
quello indicato nella definizione della function, sia
in entrata che in uscita.
• Per esempio: a=funz(b), assegna a “in1” il valore
“b”, e ad “a” il valore “out1”

41. Grafici
Per ottenere il grafico di una funzione, devo:
• Preparare un vettore di ascisse
• Preparare un vettore di ordinate
• Fare il grafico
• Esempio: grafico di cos(4x)*exp(x), su [0,2]
>> x=0:0.01:2;
>> f=cos(4*x).*exp(x);
>> plot(x,f)

42. Esercizio
Scrivere una function che calcoli la funzione esponenziale,
utilizzando i primi N termini della serie di Taylor.
Valutare l’ errore per x fissato, utilizzando come confronto la
funzione exp di Matlab, e disegnare un grafico dell’ errore in
funzione di N.

43. La function che calcola l’esponenziale può essere scritta come:
function ex=esponenziale(n,x)
% EX=ESPONENZIALE(N;X) Calcola l'esponenziale di e^x
% utilizzando i primi N termini dello sviluppo in serie
% dell'esponenziale
ex=1;
for k=1:n
den=factorial(k);
ex=ex+x.^k/den;
end

44. Mentre la function che calcola l’ errore può essere scritta così:
function err=errore_exp(n,x)
% ERR=ERRORE_EXP(N,X) Disegna un grafico dell'errore fra
% la formula di Taylor calcolata per i primi K termini,
% per k=1:N, per l' esponenziale e il
% risultato fornito dalla function EXP
% ERR(K) contiene il l'errore commesso con i primi K
% termini K=1,...,N.
for k=1:n
err(k)=abs(exp(x)-esponenziale(k,x));
end
semilogy(err)

45. Si nota che l’ errore diminuisce rapidamente, se aumento N:

46. Tuttavia, per valori di N più elevati, l’ errore non diminuisce più,
perché si è a livello dell’ errore di macchina.

47. Esempio. Grafico di una circonferenza
>> t=0:0.01:2*pi;
>> x=cos(t);
>> y=sin(t);
>> plot(x,y,'g+')
>> axis equal

48. Calcolo della norma 2 di una matrice 2 X 2
function c=norma(a)
%NORMA(A) fornisce una stima della norma 2 di una matrice 2
per 2
%costruisce il cerchio unitario e ne stampa il grafico:
t=0:0.05:2*pi;
x=cos(t);
y=sin(t);
plot(x,y)
axis equal
hold on

49. …il listato continua ...
%calcola a*[x;y] e stampa il grafico di ogni punto
c=0;
for i=1:length(t)
b=a*[x(i); y(i)];
plot(b(1),b(2),'g+')
nb = sqrt( b(1)^2 +b(2)^2 );
if nb>c
c=nb;
end
end

50. Esempio di cancellazione numerica
Calcolare (1-x)^6 con le due formule:
y1 = (1-x)^6
y2 = 1-6x +15x^2 -20x^3 +15x^4 -6x^5 +x^6
e confrontare y1 e y2 in un intorno di uno

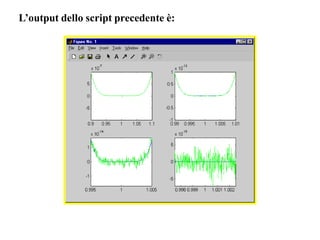
51. Esempio di cancellazione numerica
%Calcola (1-x)^6 con le due formule:
%y1 = (1-x)^6
%y2 = 1-6x +15x^2 -20x^3 +15x^4 -6x^5 +x^6
%e confronta y1 e y2 in un intorno di uno
%
k=0
for delta = [0.1, 0.01, 0.005, 0.0025]
h = delta/100;
x = 1-delta:h:1+delta;
y1 = (1-x).^6;
y2 = 1 -6*x +15*x.^2 -20*x.^3 +15*x.^4 -6*x.^5 + x.^6;
k = k+1;
subplot(2,2,k)
plot(x,y1)
hold
plot(x,y2,'g')
axis([1-delta 1+delta -max(abs(y2)) max(abs(y2)) ])
end

52. L’output dello script precedente è:

53. Istruzione subplot
L’istruzione subplot(M,N,K) crea una figura contenente
M*N
grafici, distribuiti su M righe ed N colonne.
L’indice K indica che le istruzioni seguenti si riferiscono al
K-esimo grafico, con K che varia fra 1 e M*N

54. Esercizi
1) Scrivere una function cha calcoli il valor medio di una
sequenza di numeri assegnati.
2) Scrivere una function che produca una matrice quadrata di zeri,
con degli 1 sulla diagonale che scende da destra verso sinistra.
3) Scrivere una function che disegni un rettangolo, centrato
sull’origine, con i lati assegnati in input.
4) Scrivere una function che disegni l’effetto di una matrice 2 X 2
assegnata, sul segmento S: S    x  2; y  0
1