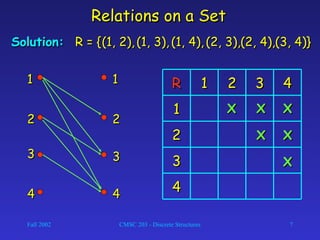
The document discusses binary relations and properties of relations. A binary relation R from set A to set B is a subset of the Cartesian product A × B. Relations can model real-world relationships between elements, like which people drive which cars. Functions are a special type of binary relation where each element of the domain A is related to exactly one element of the range B. The properties of relations discussed include reflexive, symmetric, antisymmetric, transitive, and combining relations using operations like union, intersection, and composition.






























![Fall 2002 CMSC 203 - Discrete Structures 32
Representing RelationsRepresenting Relations
We already know different ways of representingWe already know different ways of representing
relations. We will now take a closer look at tworelations. We will now take a closer look at two
ways of representation:ways of representation: Zero-one matricesZero-one matrices andand
directed graphsdirected graphs..
If R is a relation from A = {aIf R is a relation from A = {a11, a, a22, …, a, …, amm} to B =} to B =
{b{b11, b, b22, …, b, …, bnn}, then R can be represented by the}, then R can be represented by the
zero-one matrix Mzero-one matrix MRR = [m= [mijij] with] with
mmijij = 1, if (a= 1, if (aii, b, bjj))∈∈R, andR, and
mmijij = 0, if (a= 0, if (aii, b, bjj))∉∉R.R.
Note that for creating this matrix we first need toNote that for creating this matrix we first need to
list the elements in A and B in alist the elements in A and B in a particular, butparticular, but
arbitrary orderarbitrary order..](https://image.slidesharecdn.com/sadatsumon-190107174530/85/Sadat-sumon-32-320.jpg)







![Fall 2002 CMSC 203 - Discrete Structures 40
Representing Relations Using MatricesRepresenting Relations Using Matrices
Do you remember theDo you remember the Boolean productBoolean product of two zero-of two zero-
one matrices?one matrices?
Let A = [aLet A = [aijij] be an m] be an m××k zero-one matrix andk zero-one matrix and
B = [bB = [bijij] be a k] be a k××n zero-one matrix.n zero-one matrix.
Then theThen the Boolean productBoolean product of A and B, denoted byof A and B, denoted by
AAοοB, is the mB, is the m××n matrix with (i, j)th entry [cn matrix with (i, j)th entry [cijij], where], where
ccijij = (a= (ai1i1 ∧∧ bb1j1j)) ∨∨ (a(ai2i2 ∧∧ bb2i2i)) ∨∨ …… ∨∨ (a(aikik ∧∧ bbkjkj).).
ccijij = 1 if and only if at least one of the terms= 1 if and only if at least one of the terms
(a(ainin ∧∧ bbnjnj) = 1 for some n; otherwise c) = 1 for some n; otherwise cijij = 0.= 0.](https://image.slidesharecdn.com/sadatsumon-190107174530/85/Sadat-sumon-40-320.jpg)
![Fall 2002 CMSC 203 - Discrete Structures 41
Representing Relations Using MatricesRepresenting Relations Using Matrices
Let us now assume that the zero-one matricesLet us now assume that the zero-one matrices
MMAA = [a= [aijij], M], MBB = [b= [bijij] and M] and MCC = [c= [cijij] represent relations A,] represent relations A,
B, and C, respectively.B, and C, respectively.
Remember:Remember: For MFor MCC = M= MAAοοMMBB we have:we have:
ccijij = 1 if and only if at least one of the terms= 1 if and only if at least one of the terms
(a(ainin ∧∧ bbnjnj) = 1 for some n; otherwise c) = 1 for some n; otherwise cijij = 0.= 0.
In terms of theIn terms of the relationsrelations, this means that C contains a, this means that C contains a
pair (xpair (xii, z, zjj) if and only if there is an element y) if and only if there is an element ynn suchsuch
that (xthat (xii, y, ynn) is in relation A and) is in relation A and
(y(ynn, z, zjj) is in relation B.) is in relation B.
Therefore, C = BTherefore, C = B°°A (A (compositecomposite of A and B).of A and B).](https://image.slidesharecdn.com/sadatsumon-190107174530/85/Sadat-sumon-41-320.jpg)
![Fall 2002 CMSC 203 - Discrete Structures 42
Representing Relations Using MatricesRepresenting Relations Using Matrices
This gives us the following rule:This gives us the following rule:
MMBB°°AA = M= MAAοοMMBB
In other words, the matrix representing theIn other words, the matrix representing the
compositecomposite of relations A and B is theof relations A and B is the BooleanBoolean
productproduct of the matrices representing A and B.of the matrices representing A and B.
Analogously, we can find matrices representing theAnalogously, we can find matrices representing the
powers of relationspowers of relations::
MMRRnn = M= MRR
[n][n]
(n-th(n-th Boolean powerBoolean power).).](https://image.slidesharecdn.com/sadatsumon-190107174530/85/Sadat-sumon-42-320.jpg)
![Fall 2002 CMSC 203 - Discrete Structures 43
Representing Relations Using MatricesRepresenting Relations Using Matrices
Example:Example: Find the matrix representing RFind the matrix representing R22
, where, where
the matrix representing R is given bythe matrix representing R is given by
=
001
110
010
RM
Solution:Solution: The matrix for RThe matrix for R22
is given byis given by
==
010
111
110
]2[
2 RR
MM](https://image.slidesharecdn.com/sadatsumon-190107174530/85/Sadat-sumon-43-320.jpg)






![Fall 2002 CMSC 203 - Discrete Structures 50
Equivalence ClassesEquivalence Classes
Definition:Definition: Let R be an equivalence relation on aLet R be an equivalence relation on a
set A. The set of all elements that are related toset A. The set of all elements that are related to
an element a of A is called thean element a of A is called the equivalence classequivalence class
of a.of a.
The equivalence class of a with respect to R isThe equivalence class of a with respect to R is
denoted bydenoted by [a][a]RR..
When only one relation is under consideration, weWhen only one relation is under consideration, we
will delete the subscript R and writewill delete the subscript R and write [a][a] for thisfor this
equivalence class.equivalence class.
If bIf b∈∈[a][a]RR, b is called a, b is called a representativerepresentative of thisof this
equivalence class.equivalence class.](https://image.slidesharecdn.com/sadatsumon-190107174530/85/Sadat-sumon-50-320.jpg)
![Fall 2002 CMSC 203 - Discrete Structures 51
Equivalence ClassesEquivalence Classes
Example:Example: In the previous example (strings ofIn the previous example (strings of
identical length), what is the equivalence class ofidentical length), what is the equivalence class of
the word mouse, denoted by [mouse] ?the word mouse, denoted by [mouse] ?
Solution:Solution: [mouse] is the set of all English words[mouse] is the set of all English words
containing five letters.containing five letters.
For example, ‘horse’ would be a representative ofFor example, ‘horse’ would be a representative of
this equivalence class.this equivalence class.](https://image.slidesharecdn.com/sadatsumon-190107174530/85/Sadat-sumon-51-320.jpg)
![Fall 2002 CMSC 203 - Discrete Structures 52
Equivalence ClassesEquivalence Classes
Theorem:Theorem: Let R be an equivalence relation on a setLet R be an equivalence relation on a set
A. The following statements are equivalent:A. The following statements are equivalent:
• aRbaRb
• [a] = [b][a] = [b]
• [a][a] ∩∩ [b][b] ≠≠ ∅∅
Definition:Definition: AA partitionpartition of a set S is a collection ofof a set S is a collection of
disjoint nonempty subsets of S that have S as theirdisjoint nonempty subsets of S that have S as their
union. In other words, the collection of subsets Aunion. In other words, the collection of subsets Aii,,
ii∈∈I, forms a partition of S if and only ifI, forms a partition of S if and only if
(i) A(i) Aii ≠≠ ∅∅ for ifor i∈∈II
• AAii ∩∩ AAjj == ∅∅, if i, if i ≠≠ jj
• ∪∪ii∈∈II AAii = S= S](https://image.slidesharecdn.com/sadatsumon-190107174530/85/Sadat-sumon-52-320.jpg)




