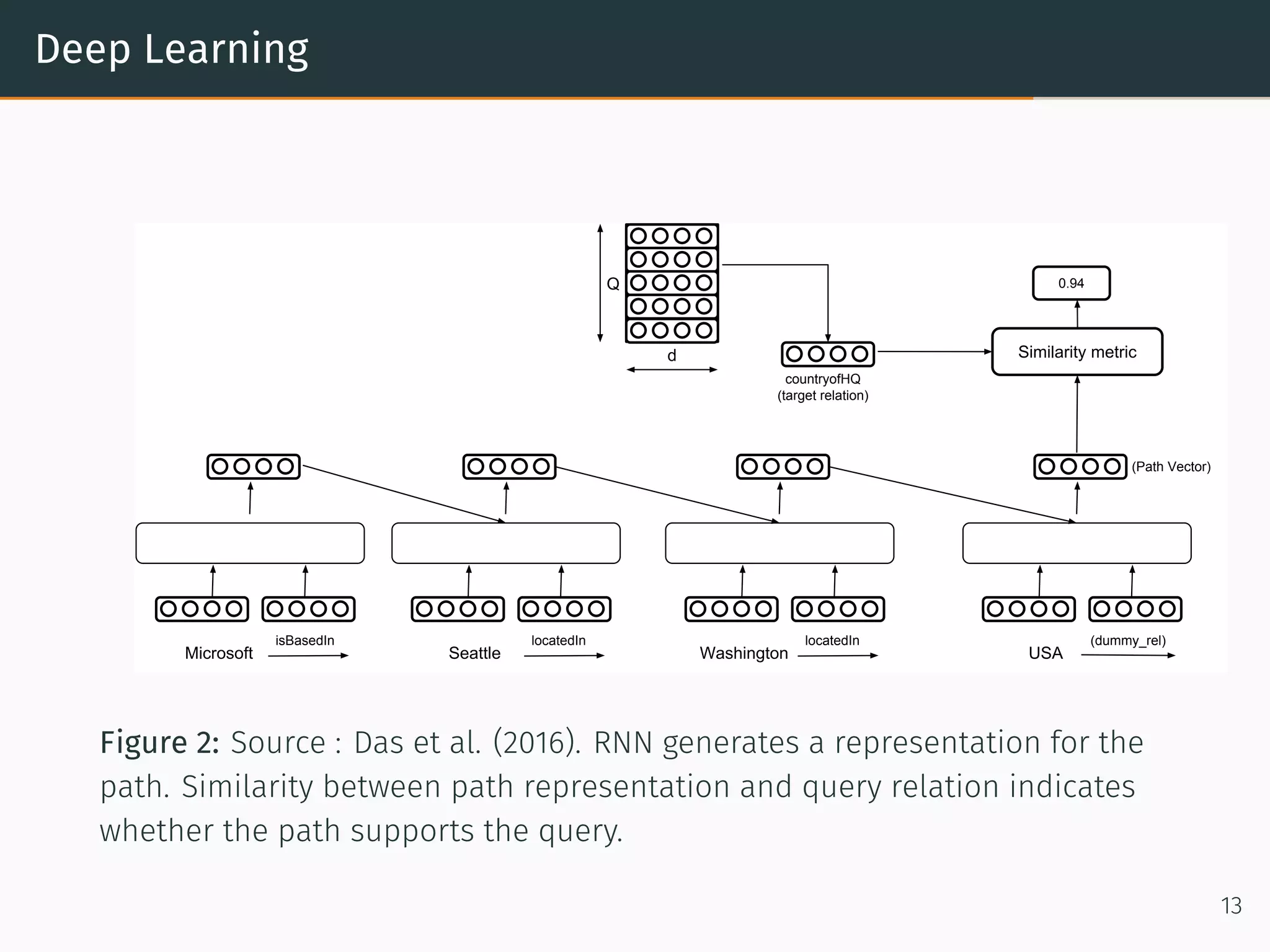
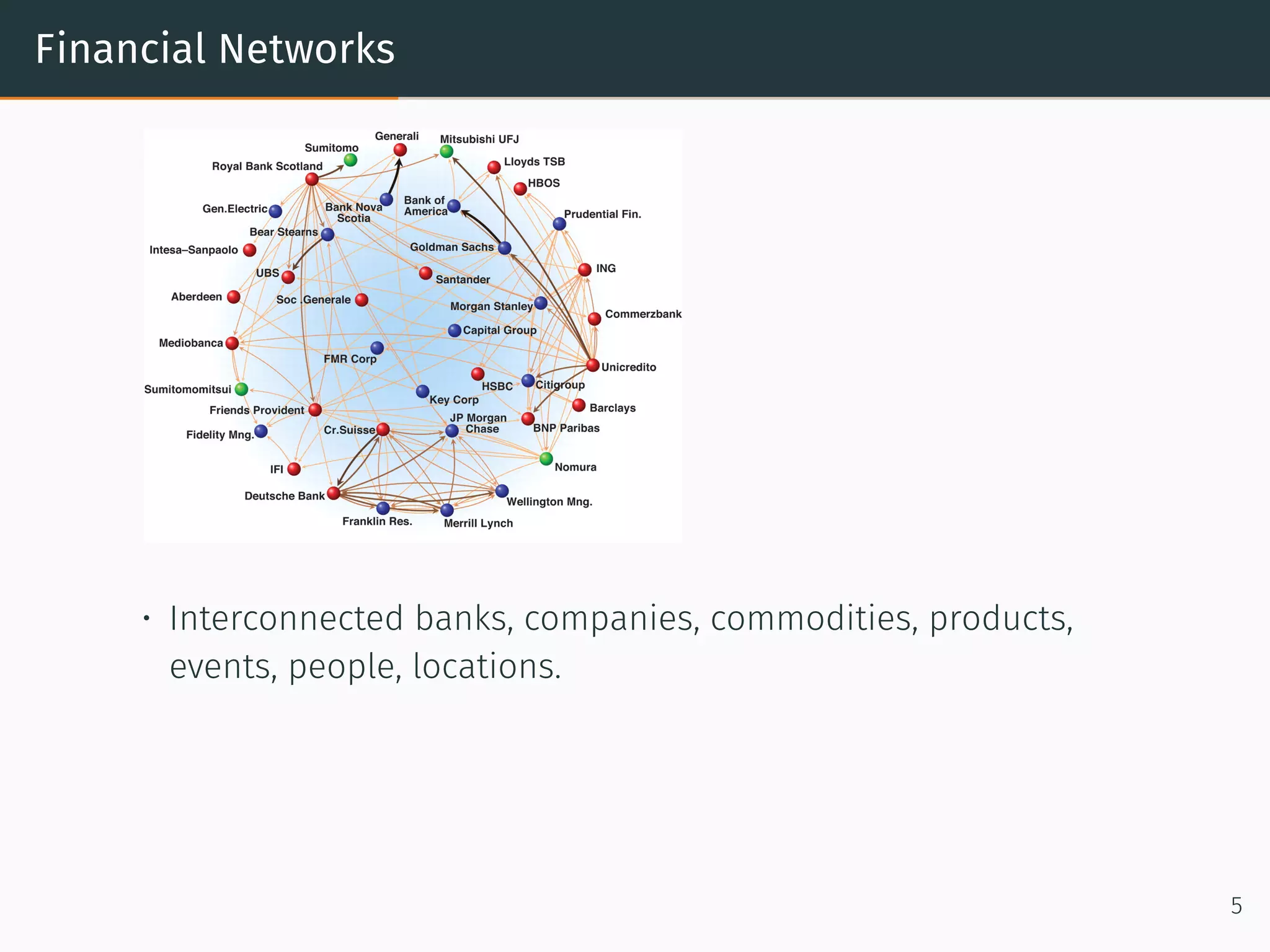
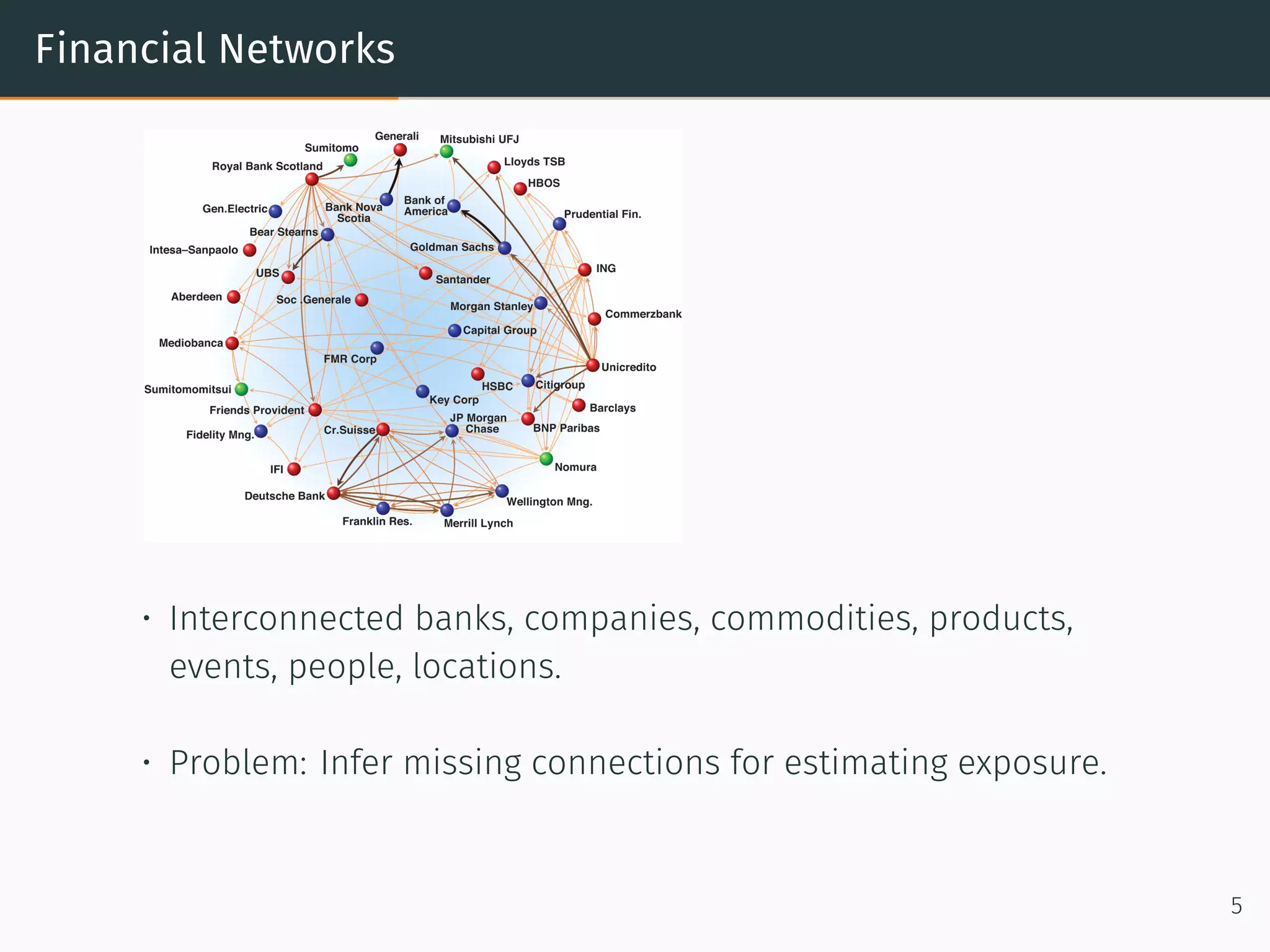
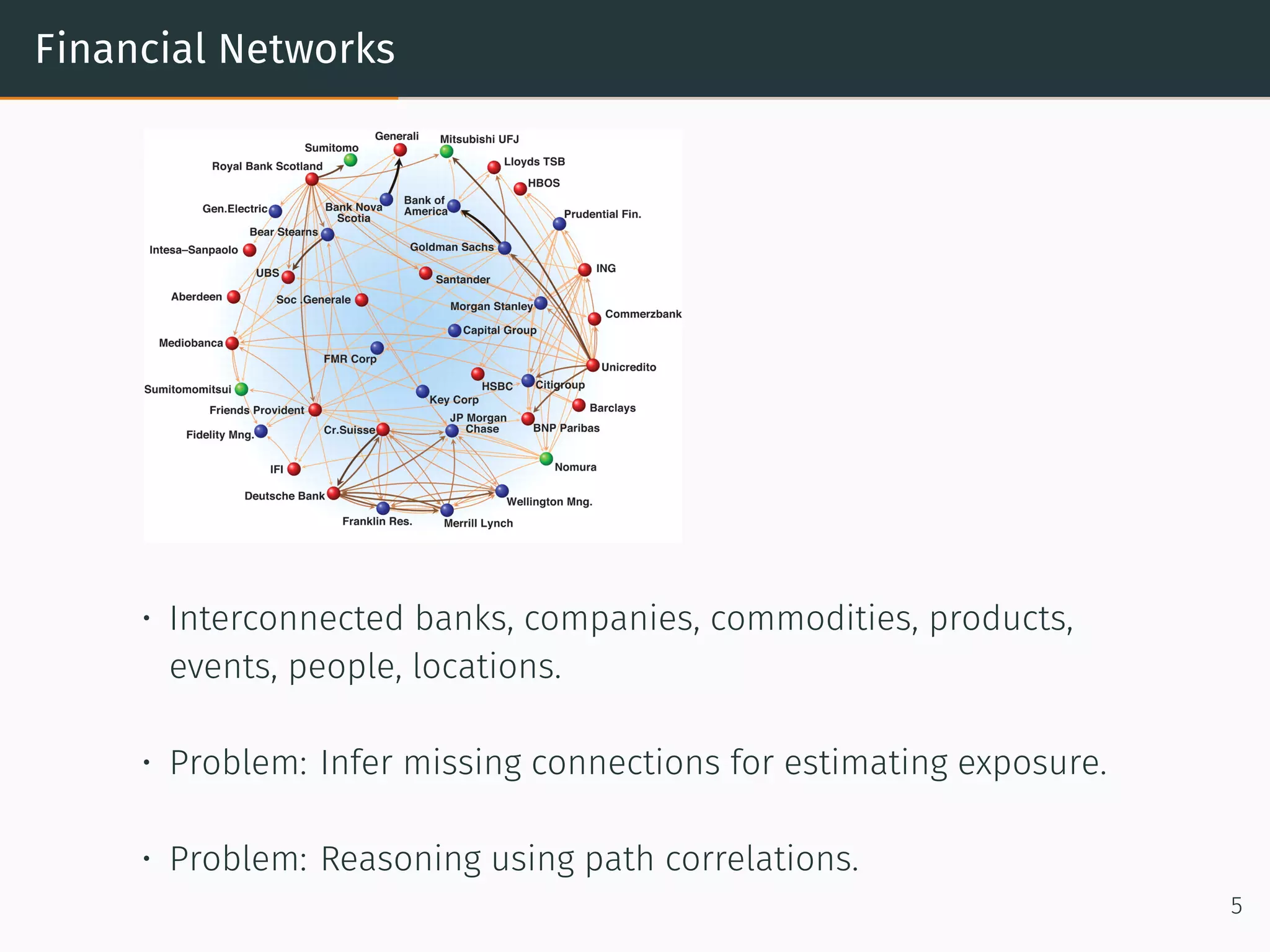
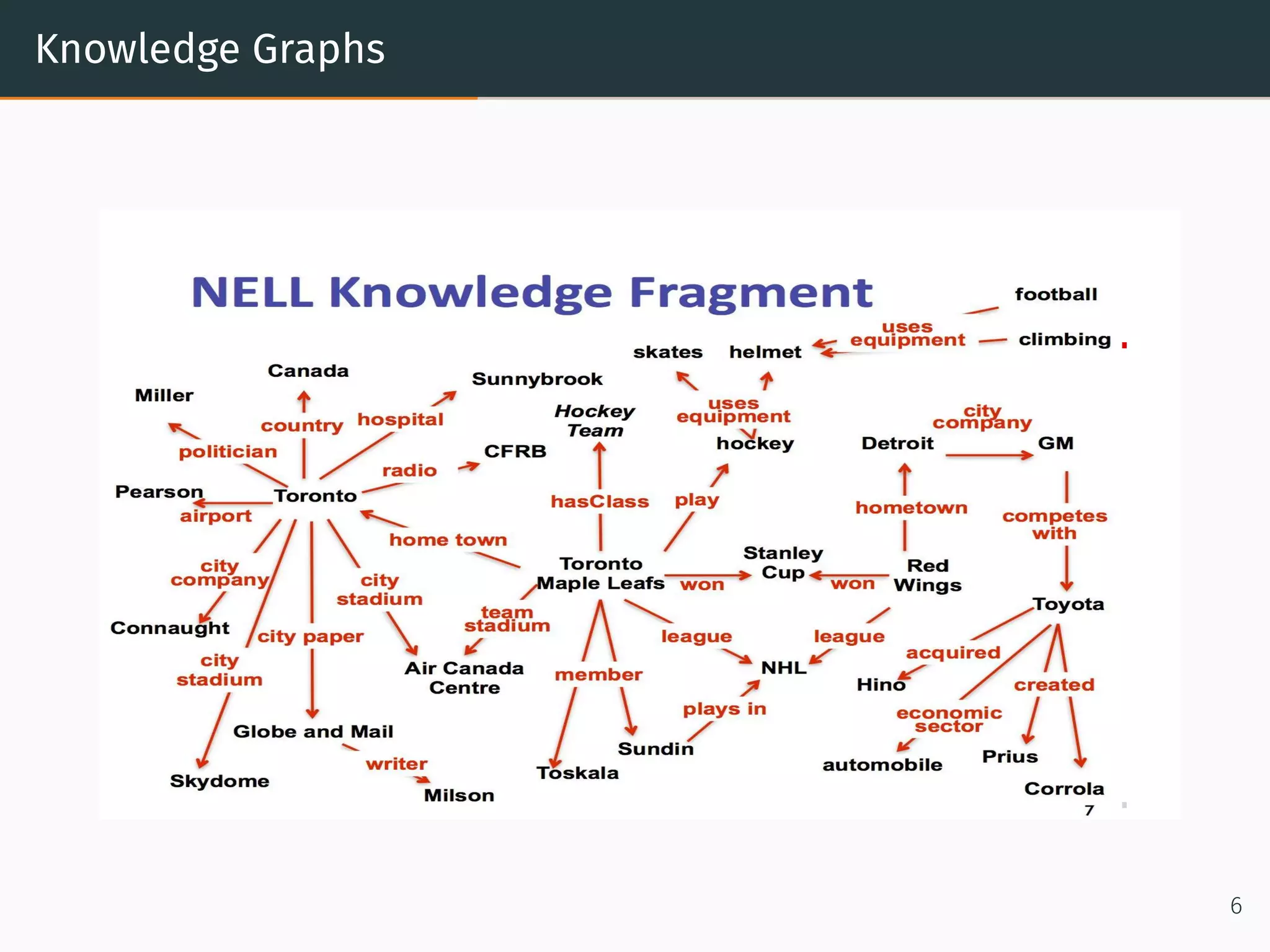
This document provides an overview of relational machine learning models and applications. It discusses how networks and graphs like social networks, biological networks, financial networks, and knowledge graphs can be modeled using relational machine learning. Specific models discussed include recommendation engines that use matrix factorization, the RESCAL model for multi-relational data, bilinear diagonal models for scalability, and TransE which models relationships as translations in the embedding space. The document also covers generating negative samples and different loss functions used for training these models.

1. Relational Machine Learning
Applications and Models
Bhushan Kotnis
Heidelberg University

2. Table of contents
1. Introduction
2. Models
1

3. Introduction

4. Networks and Graphs
• Social Networks : Link Prediction, Relevant Ads, Feed
Recommendation.
2

5. Networks and Graphs
• Social Networks : Link Prediction, Relevant Ads, Feed
Recommendation.
• Biological Networks: Gene Ontology, Protein Interaction
Networks, Cellular Networks.
2

6. Networks and Graphs
• Social Networks : Link Prediction, Relevant Ads, Feed
Recommendation.
• Biological Networks: Gene Ontology, Protein Interaction
Networks, Cellular Networks.
• Financial Networks: Assessing risk and exposure, providing
information, detecting fraud
2

7. Networks and Graphs
• Social Networks : Link Prediction, Relevant Ads, Feed
Recommendation.
• Biological Networks: Gene Ontology, Protein Interaction
Networks, Cellular Networks.
• Financial Networks: Assessing risk and exposure, providing
information, detecting fraud
• Knowledge Graphs: Background knowledge for AI, intelligent
search engines.
2

8. Social Networks
• Problem: Rank Ads/Feeds, suggest relevant articles.
3

9. Social Networks
• Problem: Rank Ads/Feeds, suggest relevant articles.
• Users are connected to one another, share interests,
demographic data, news preferences.
3

10. Social Networks
• Problem: Rank Ads/Feeds, suggest relevant articles.
• Users are connected to one another, share interests,
demographic data, news preferences.
• Linked Machine Learning problem: Predict ads, article
recommendation, feed, etc using a unified model. 3

11. Genetic Regulatory Network
• Genes Regulatory Network: Molecular interaction network,
Genes interacting with proteins and other molecules.
4

12. Genetic Regulatory Network
• Genes Regulatory Network: Molecular interaction network,
Genes interacting with proteins and other molecules.
• Problem: Infer family, function of the Gene based on its
interactions. Mutations leading to diseases.
4

13. Genetic Regulatory Network
• Genes Regulatory Network: Molecular interaction network,
Genes interacting with proteins and other molecules.
• Problem: Infer family, function of the Gene based on its
interactions. Mutations leading to diseases.
• Link prediction problem: Linked ML problem because a
prediction depends on other predictions.
4

14. Financial Networks
• Interconnected banks, companies, commodities, products,
events, people, locations.
5

15. Financial Networks
• Interconnected banks, companies, commodities, products,
events, people, locations.
• Problem: Infer missing connections for estimating exposure.
5

16. Financial Networks
• Interconnected banks, companies, commodities, products,
events, people, locations.
• Problem: Infer missing connections for estimating exposure.
• Problem: Reasoning using path correlations.
5

17. Knowledge Graphs
6

18. The KGC Problem
• Knowledge Graph : G set of triples (s, r, t), s, t ∈ E and r ∈ R.
7

19. The KGC Problem
• Knowledge Graph : G set of triples (s, r, t), s, t ∈ E and r ∈ R.
• Ranking Problem: Query (s, r, ?) target set e1, e2, en. Rank targets
based on plausibility of relation r existing between s and ei.
7

20. The KGC Problem
• Knowledge Graph : G set of triples (s, r, t), s, t ∈ E and r ∈ R.
• Ranking Problem: Query (s, r, ?) target set e1, e2, en. Rank targets
based on plausibility of relation r existing between s and ei.
• (Frankfurt, cityliesonriver, ?) Choices: Rhine, Mosel, Thames,
Main, Hudson.
7

21. The KGC Problem
• Knowledge Graph : G set of triples (s, r, t), s, t ∈ E and r ∈ R.
• Ranking Problem: Query (s, r, ?) target set e1, e2, en. Rank targets
based on plausibility of relation r existing between s and ei.
• (Frankfurt, cityliesonriver, ?) Choices: Rhine, Mosel, Thames,
Main, Hudson.
• (user_id_201345, user_prefers_genre, ?) Choices: Fiction,
Non-Fiction, Horror, Romance, Fantasy.
7

22. The KGC Problem
• Knowledge Graph : G set of triples (s, r, t), s, t ∈ E and r ∈ R.
• Ranking Problem: Query (s, r, ?) target set e1, e2, en. Rank targets
based on plausibility of relation r existing between s and ei.
• (Frankfurt, cityliesonriver, ?) Choices: Rhine, Mosel, Thames,
Main, Hudson.
• (user_id_201345, user_prefers_genre, ?) Choices: Fiction,
Non-Fiction, Horror, Romance, Fantasy.
• (TP53, disease, ?) Choices: none, Breast Cancer, Liver Cancer,
Lung Cancer.
7

23. Models

24. Recommendation Engines
• Recommend Movies. ui: vector representing user i and vi
represents product i. u, v ∈ Rd
.
8

25. Recommendation Engines
• Recommend Movies. ui: vector representing user i and vi
represents product i. u, v ∈ Rd
.
• Minimize
∑
i,j(ri,j − uT
i vj)2
+ Regularizer
8

26. Recommendation Engines
• Recommend Movies. ui: vector representing user i and vi
represents product i. u, v ∈ Rd
.
• Minimize
∑
i,j(ri,j − uT
i vj)2
+ Regularizer
• If rating ri,j is very high then we want high similarity (dot
product) between user and product vectors.
8

27. Recommendation Engines
• Recommend Movies. ui: vector representing user i and vi
represents product i. u, v ∈ Rd
.
• Minimize
∑
i,j(ri,j − uT
i vj)2
+ Regularizer
• If rating ri,j is very high then we want high similarity (dot
product) between user and product vectors.
• These vectors are called latent factors. Not interpretable, could
be genre, topics, themes. Help generalization.
8

28. Recommendation Engines
• Recommend Movies. ui: vector representing user i and vi
represents product i. u, v ∈ Rd
.
• Minimize
∑
i,j(ri,j − uT
i vj)2
+ Regularizer
• If rating ri,j is very high then we want high similarity (dot
product) between user and product vectors.
• These vectors are called latent factors. Not interpretable, could
be genre, topics, themes. Help generalization.
• Initialize them randomly and learn using SGD. They capture the
structure of the matrix.
8

29. RESCAL Model
• Capture Graph structure. Graph has multiple relations: users ×
products, users × demographics, products × Categories.
9

30. RESCAL Model
• Capture Graph structure. Graph has multiple relations: users ×
products, users × demographics, products × Categories.
• Solution: One matrix factorization problem for every relation.
9

31. RESCAL Model
• Capture Graph structure. Graph has multiple relations: users ×
products, users × demographics, products × Categories.
• Solution: One matrix factorization problem for every relation.
• f (s, r, t) = xT
s Wr xt. Where (xs, xt) ∈ Rd
, Wr ∈ Rd×d
9

32. RESCAL Model
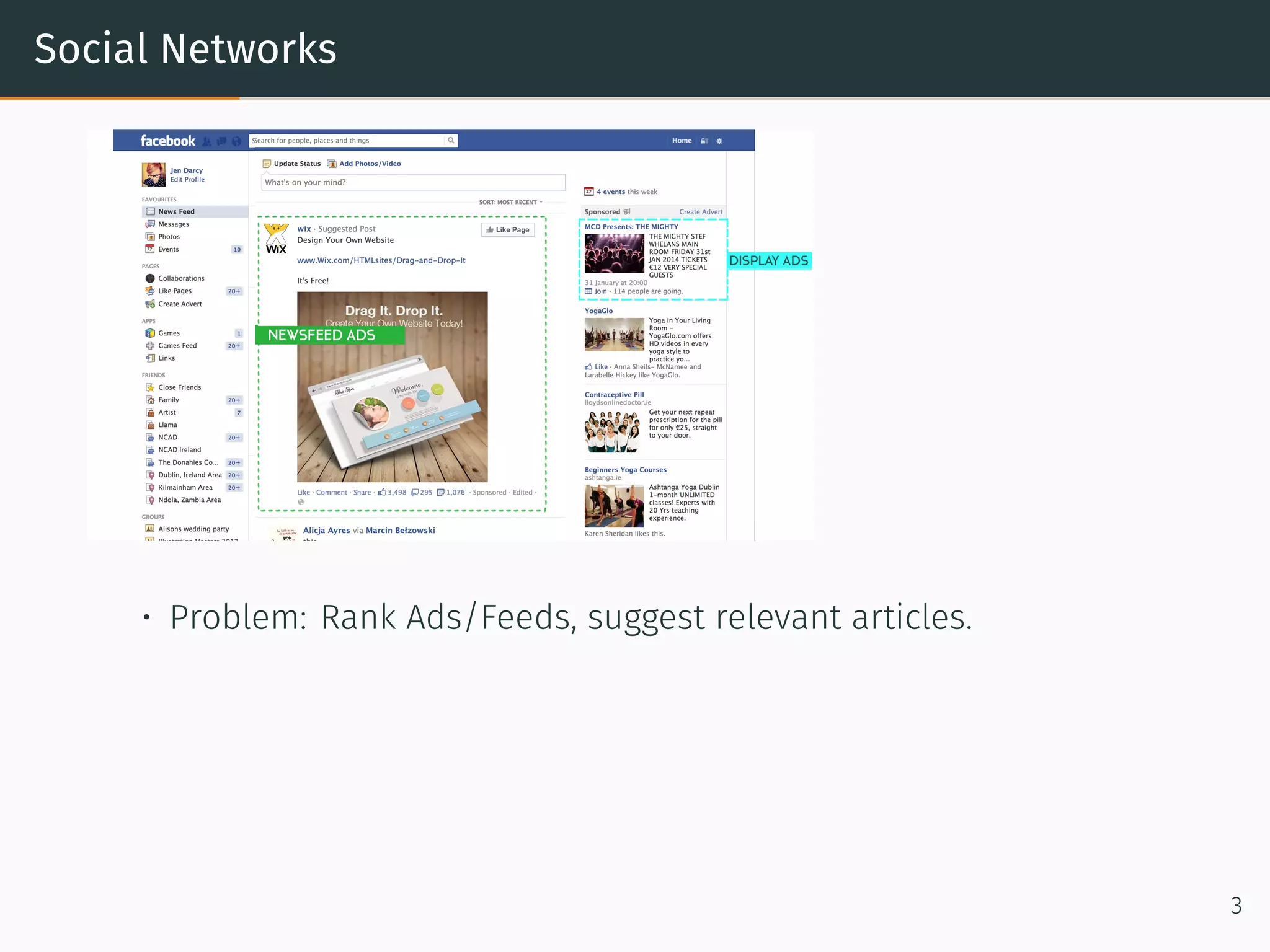
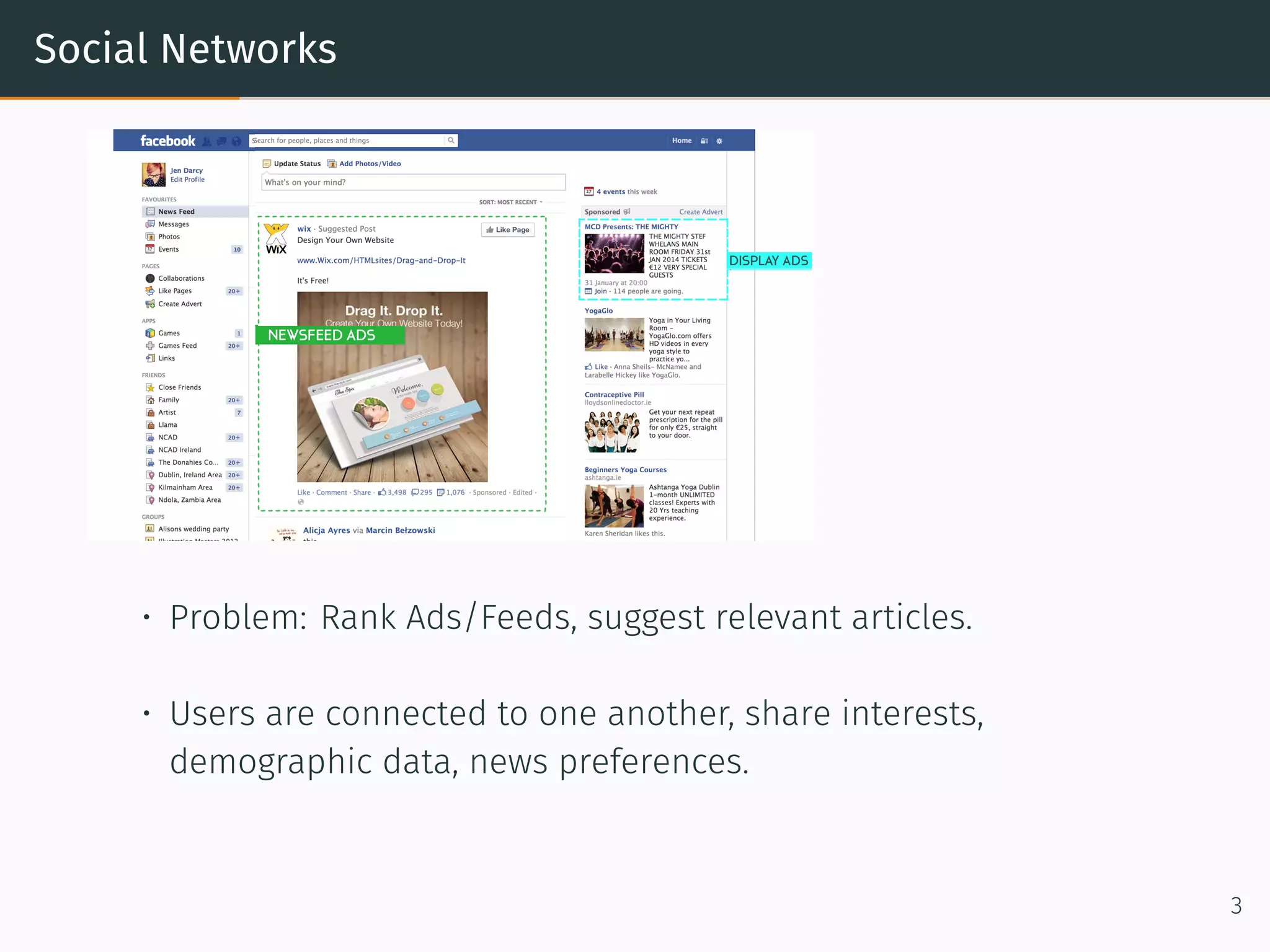
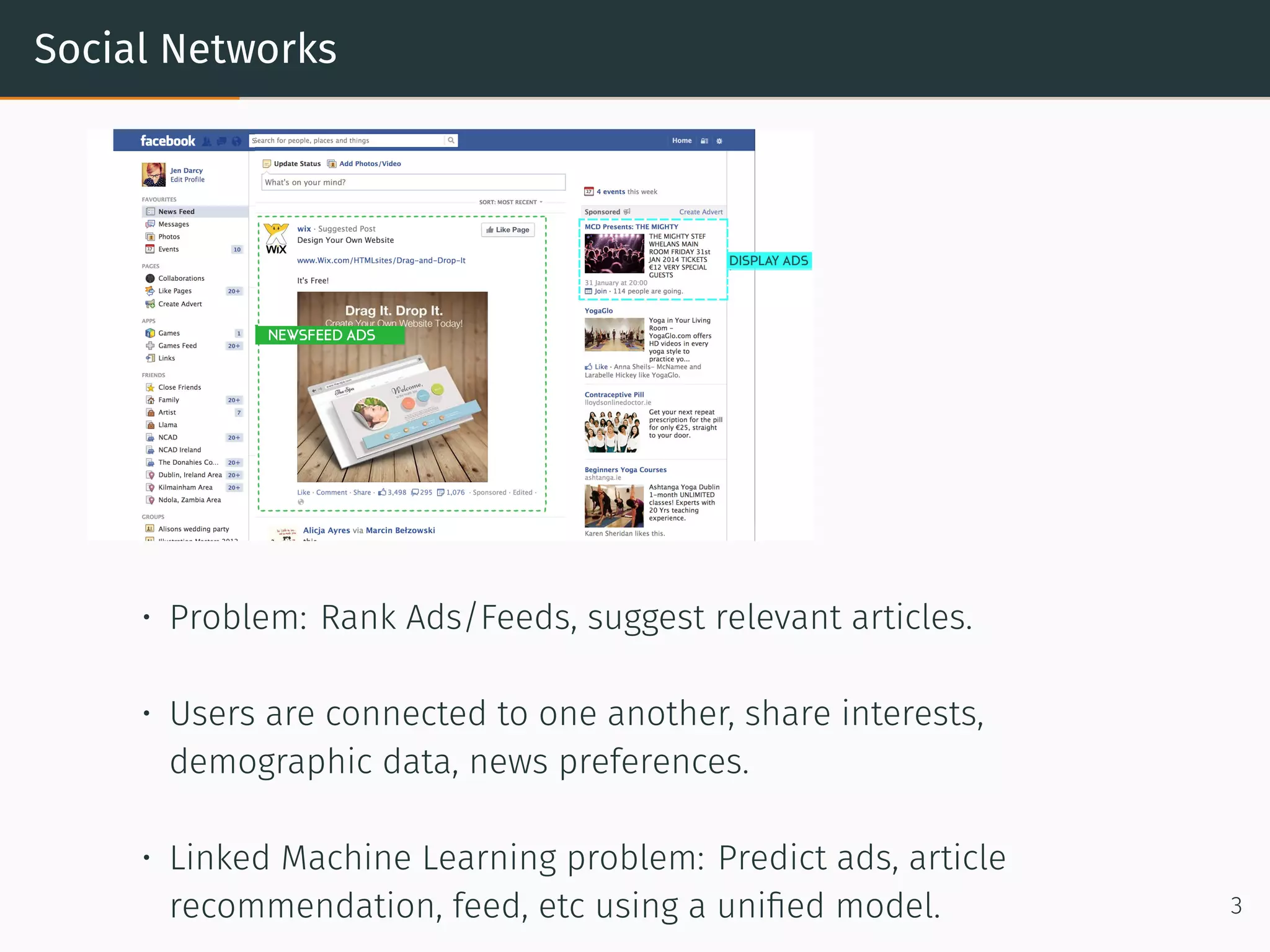
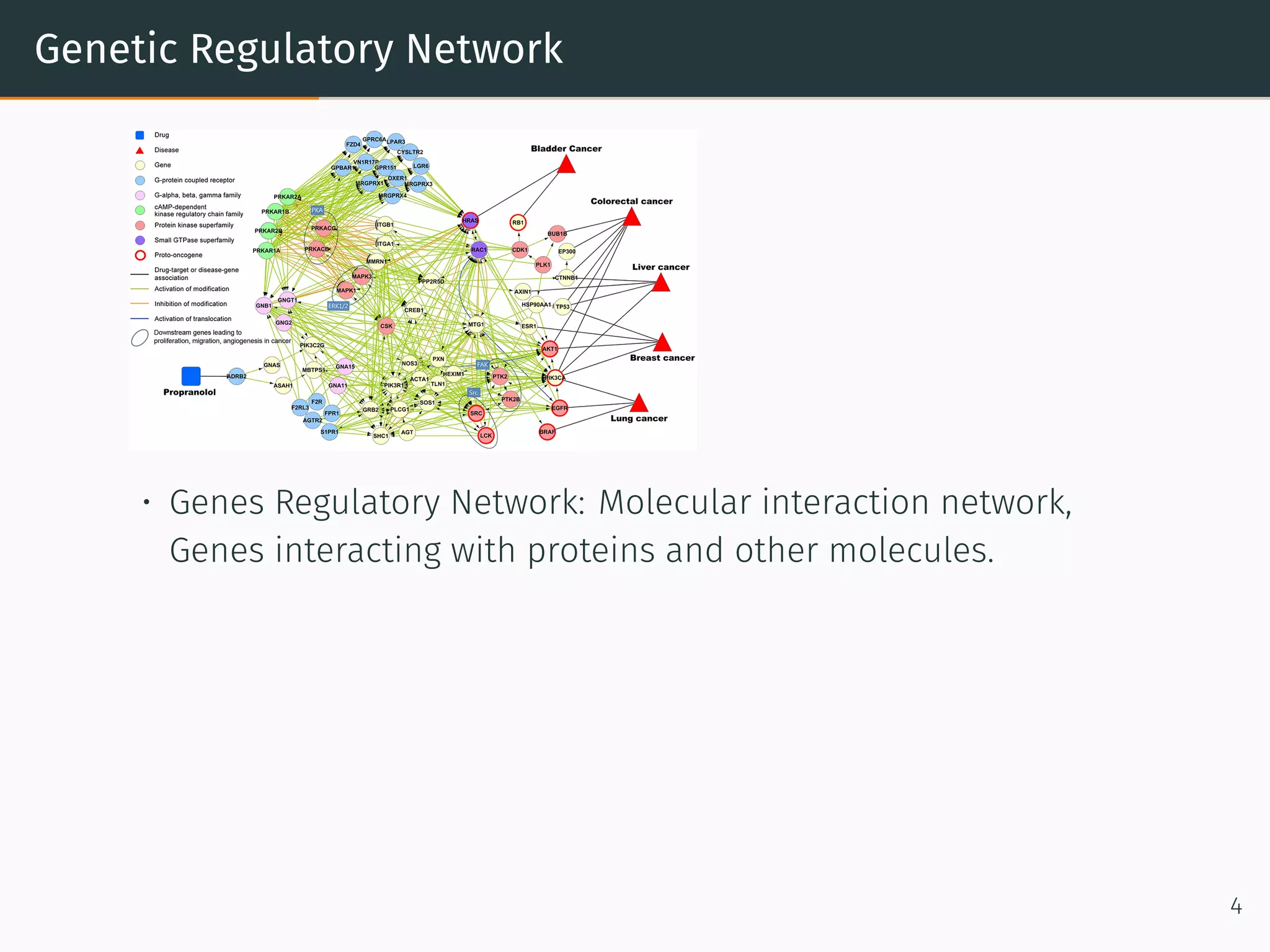
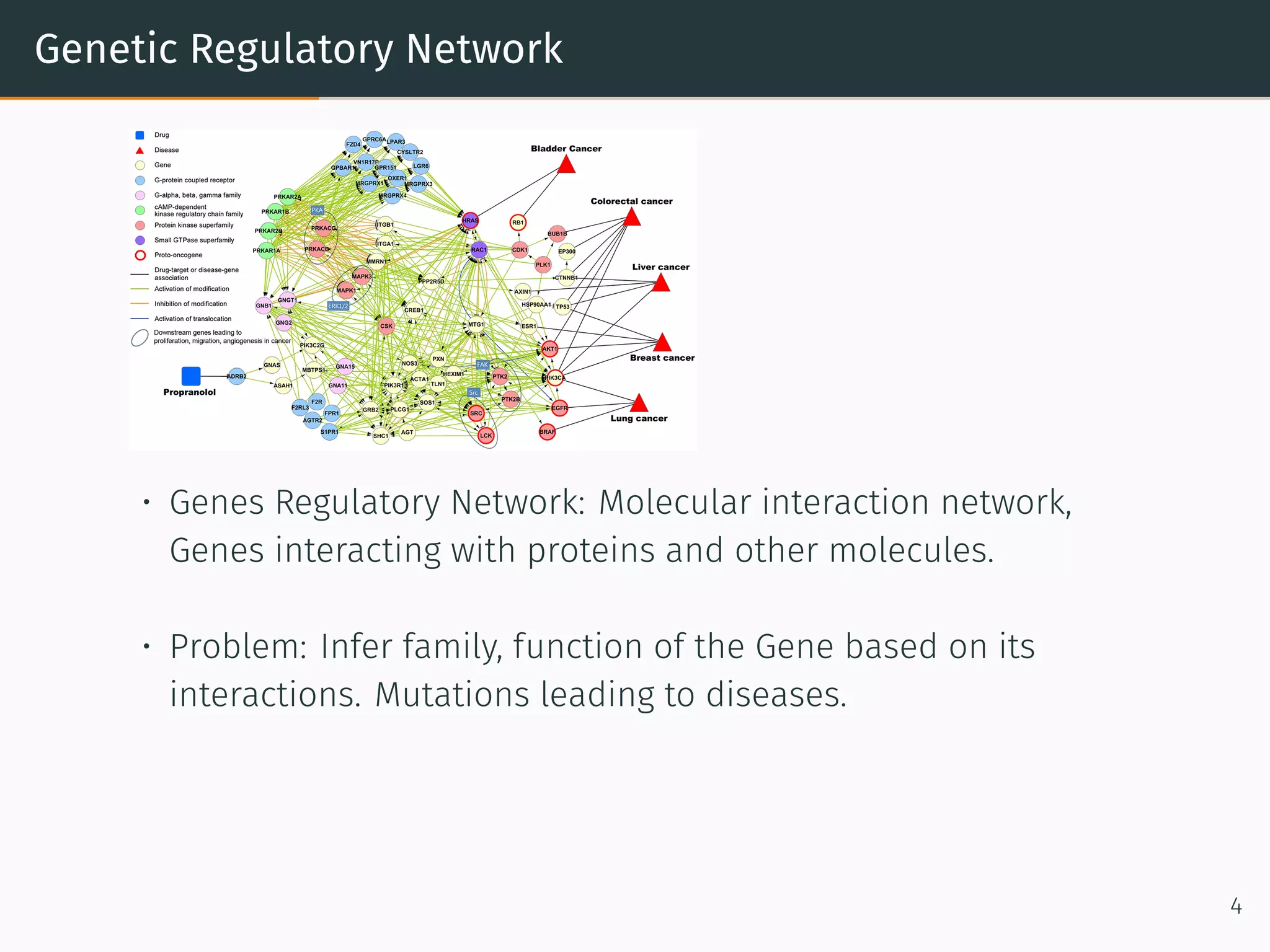
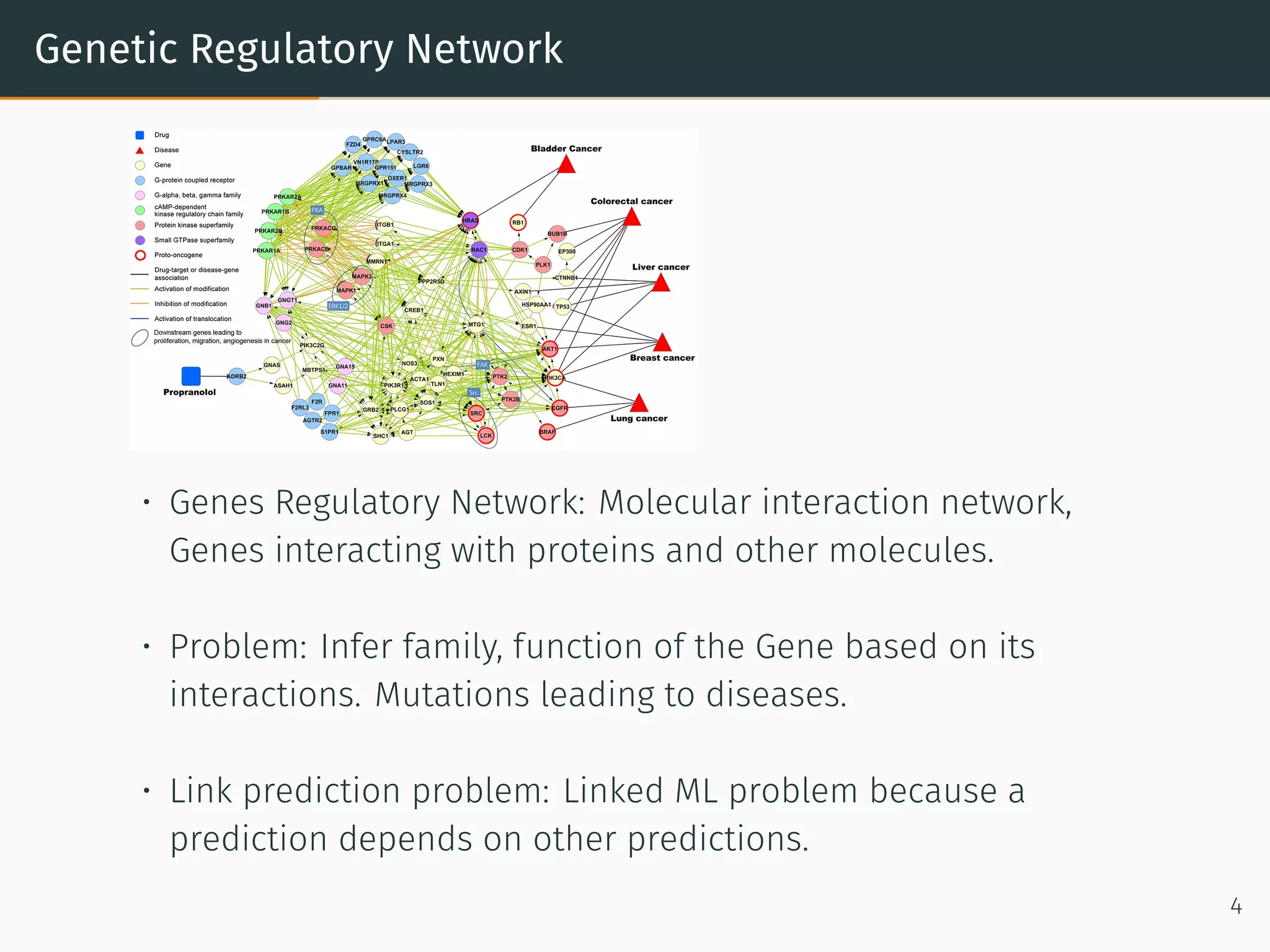
• Capture Graph structure. Graph has multiple relations: users ×
products, users × demographics, products × Categories.
• Solution: One matrix factorization problem for every relation.
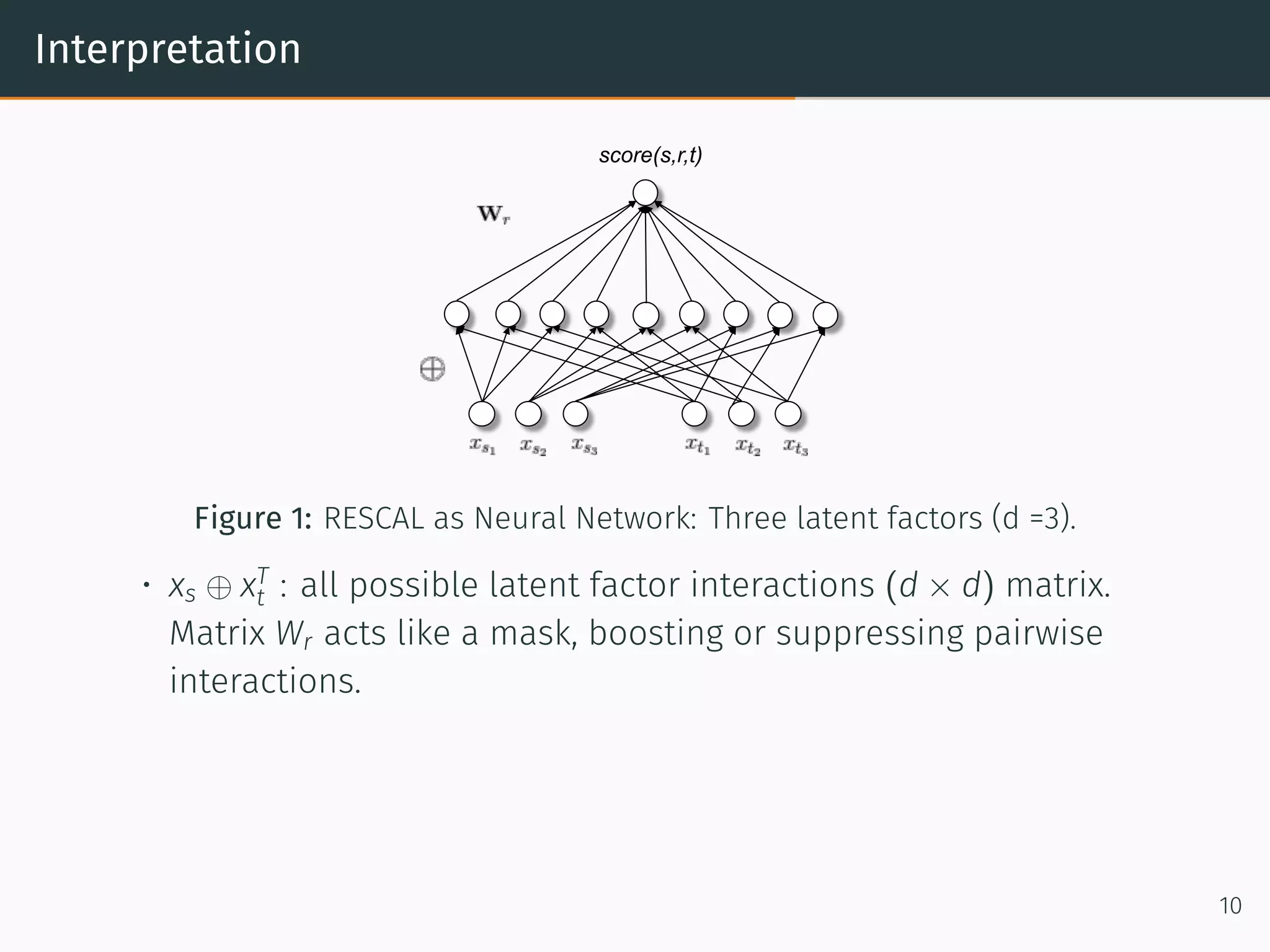
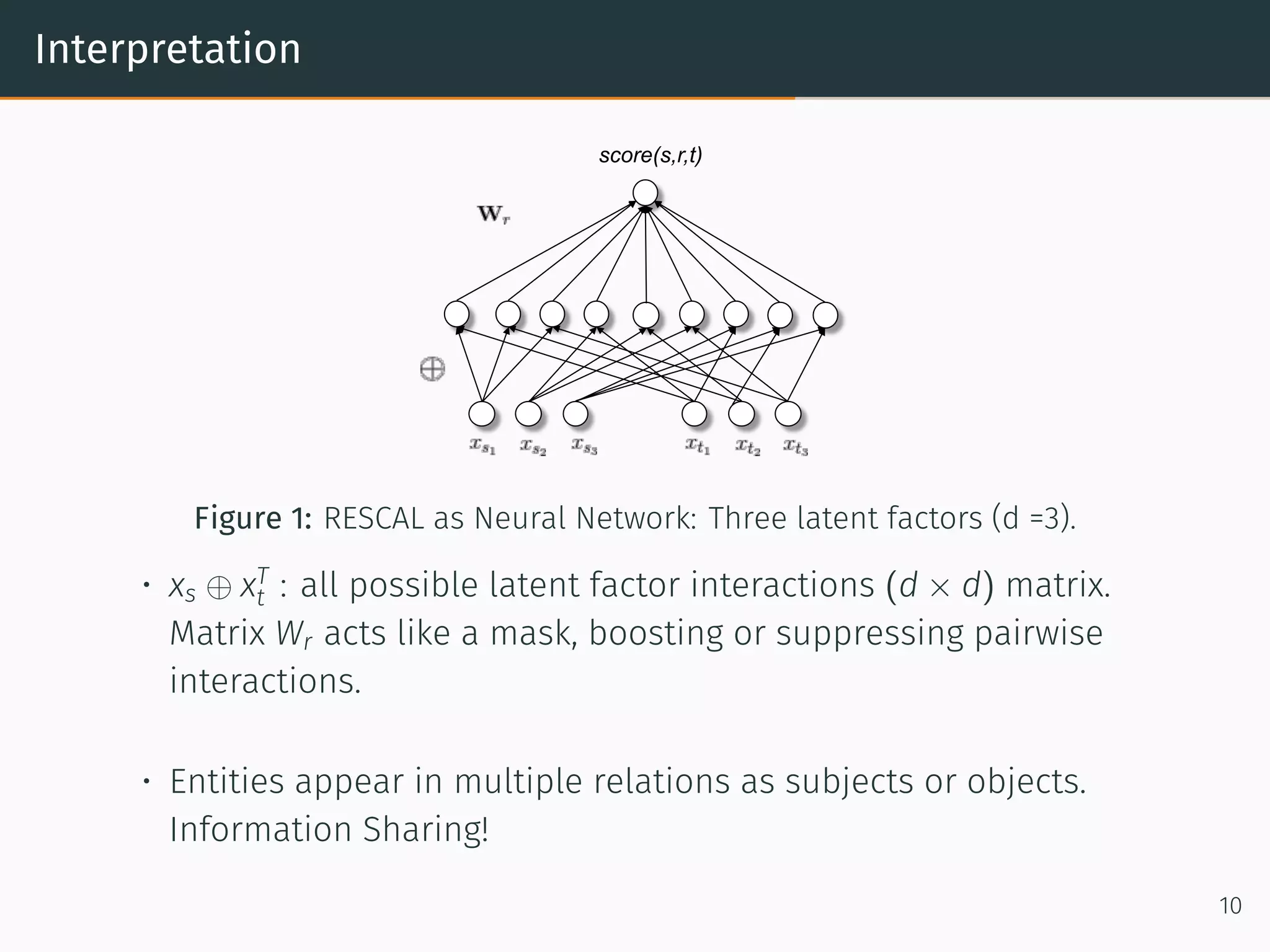
• f (s, r, t) = xT
s Wr xt. Where (xs, xt) ∈ Rd
, Wr ∈ Rd×d
• Max-Margin: max
[
0, 1 −
(
f(s, r, t) − f(s, r, t′
)
)
]
. Can also use
softmax, or l2 loss like collaborative filtering.
9

33. Interpretation
score(s,r,t)
Figure 1: RESCAL as Neural Network: Three latent factors (d =3).
• xs ⊕ xT
t : all possible latent factor interactions (d × d) matrix.
Matrix Wr acts like a mask, boosting or suppressing pairwise
interactions.
10

34. Interpretation
score(s,r,t)
Figure 1: RESCAL as Neural Network: Three latent factors (d =3).
• xs ⊕ xT
t : all possible latent factor interactions (d × d) matrix.
Matrix Wr acts like a mask, boosting or suppressing pairwise
interactions.
• Entities appear in multiple relations as subjects or objects.
Information Sharing!
10

35. Billinear Diag. and TransE Model
• RESCAL [2]: Requires O(Ned + Nrd2
) parameters. Scalability
issues for large Nr.
11

36. Billinear Diag. and TransE Model
• RESCAL [2]: Requires O(Ned + Nrd2
) parameters. Scalability
issues for large Nr.
• Bilinear Diag [4]: Enforce Wr to be a diagonal matrix. Assumes
symmetric relations. Why? Memory Complexity : O(Ned + Nrd)
11

37. Billinear Diag. and TransE Model
• RESCAL [2]: Requires O(Ned + Nrd2
) parameters. Scalability
issues for large Nr.
• Bilinear Diag [4]: Enforce Wr to be a diagonal matrix. Assumes
symmetric relations. Why? Memory Complexity : O(Ned + Nrd)
• TransE [1] : f(s, r, t) = −||(xs + xr) − xt||2.
11

38. Billinear Diag. and TransE Model
• RESCAL [2]: Requires O(Ned + Nrd2
) parameters. Scalability
issues for large Nr.
• Bilinear Diag [4]: Enforce Wr to be a diagonal matrix. Assumes
symmetric relations. Why? Memory Complexity : O(Ned + Nrd)
• TransE [1] : f(s, r, t) = −||(xs + xr) − xt||2.
• TransE : Can it model all types of relations. Why?
11

39. Billinear Diag. and TransE Model
• RESCAL [2]: Requires O(Ned + Nrd2
) parameters. Scalability
issues for large Nr.
• Bilinear Diag [4]: Enforce Wr to be a diagonal matrix. Assumes
symmetric relations. Why? Memory Complexity : O(Ned + Nrd)
• TransE [1] : f(s, r, t) = −||(xs + xr) − xt||2.
• TransE : Can it model all types of relations. Why?
• Takeaway: Make sure parameters are shared. Either shared
representation or shared layer.
11

40. Negative Sampling
• How to generate negative samples? Negatives may not be
provided.
12

41. Negative Sampling
• How to generate negative samples? Negatives may not be
provided.
• Closed World Assumption: If not a positive then must be a
negative.
12

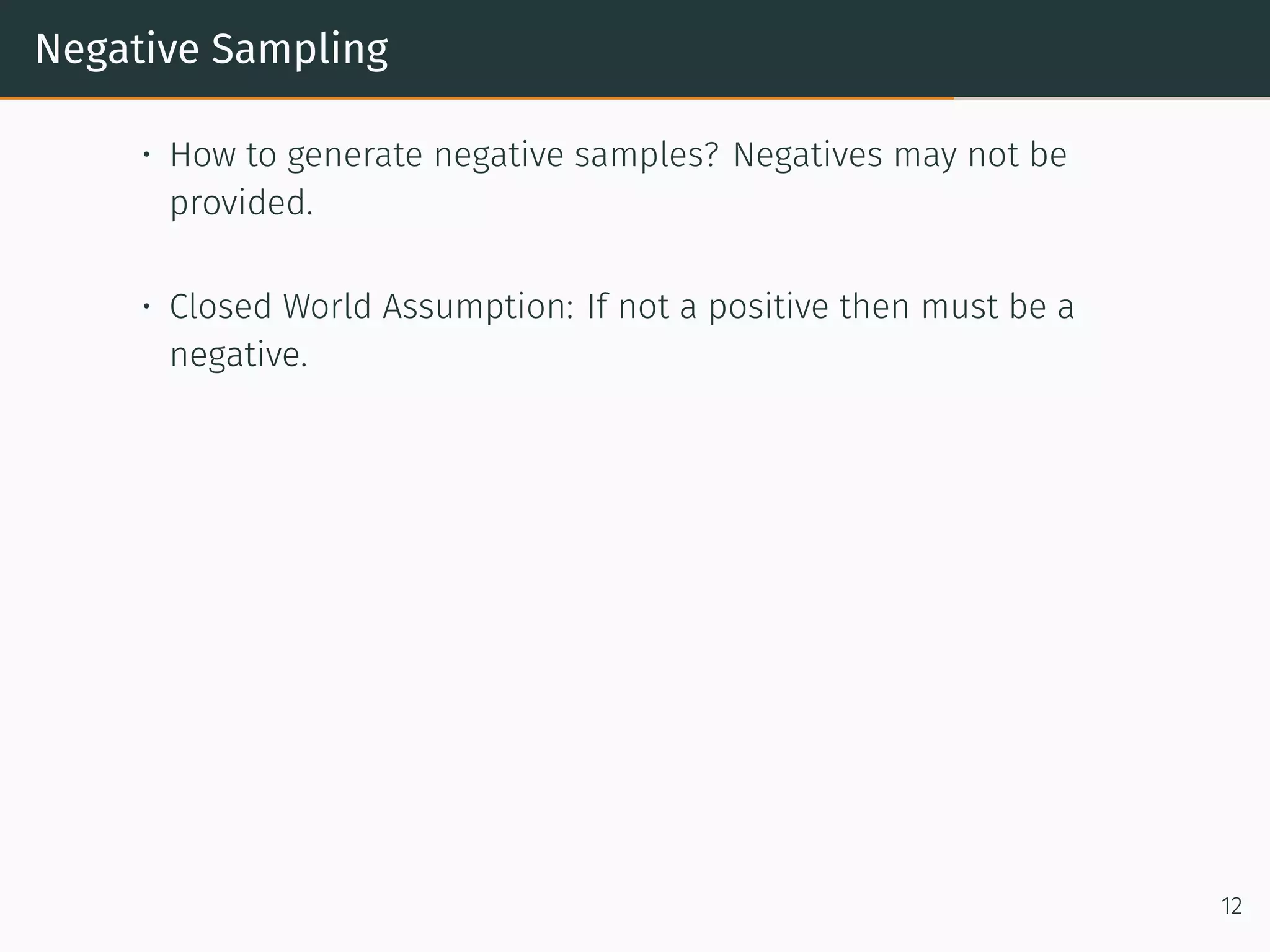
42. Negative Sampling
• How to generate negative samples? Negatives may not be
provided.
• Closed World Assumption: If not a positive then must be a
negative.
• Max-Margin: max
[
0, 1 −
(
f(s, r, t) − f(s, r, t′
)
)
]
. Softer negatives:
(s, r,′
t′
) more negative than (s, r, t)
12

43. Negative Sampling
• How to generate negative samples? Negatives may not be
provided.
• Closed World Assumption: If not a positive then must be a
negative.
• Max-Margin: max
[
0, 1 −
(
f(s, r, t) − f(s, r, t′
)
)
]
. Softer negatives:
(s, r,′
t′
) more negative than (s, r, t)
• Soft Max Loss : log(1 + exp(−yif(si, ri, ti)). Negatives are ‘really’
negative.
12

44. Negative Sampling
• How to generate negative samples? Negatives may not be
provided.
• Closed World Assumption: If not a positive then must be a
negative.
• Max-Margin: max
[
0, 1 −
(
f(s, r, t) − f(s, r, t′
)
)
]
. Softer negatives:
(s, r,′
t′
) more negative than (s, r, t)
• Soft Max Loss : log(1 + exp(−yif(si, ri, ti)). Negatives are ‘really’
negative.
• Number of negative samples during training affect performance.
See [3].
12

45. Deep Learning
countryofHQ
(target relation)
Similarity metric
0.94
d
Q
Microsoft
isBasedIn
Seattle
locatedIn
USA
(dummy_rel)
Washington
locatedIn
(Path Vector)
Figure 2: At each step, the RNN consumes both entity and relation vectors of the path. The
representation can be obtained from its types. The path vector yπ is the last hidden state. The para
of the RNN and relation embeddings are shared across all query relations. The dot product b
the final representation of the path and the query relation gives a confidence score, with higher
indicating that the query relation exists between the entity pair.
Figure 2: Source : Das et al. (2016). RNN generates a representation for the
path. Similarity between path representation and query relation indicates
whether the path supports the query.
13

46. Questions
I am convinced that the crux of the problem of learning is
recognizing relationships and being able to use them.
Christopher Strachey in a letter to Alan Turing, 1954.
14

47. References I
A. Bordes, N. Usunier, A. Garcia-Duran, J. Weston, and
O. Yakhnenko.
Translating embeddings for modeling multi-relational data.
In C. J. C. Burges, L. Bottou, M. Welling, Z. Ghahramani, and K. Q.
Weinberger, editors, Advances in Neural Information Processing
Systems 26, pages 2787–2795. Curran Associates, Inc., 2013.
M. Nickel, V. Tresp, and H.-P. Kriegel.
A three-way model for collective learning on multi-relational
data.
In ICML, 2011.
15

48. References II
T. Trouillon, C. R. Dance, J. Welbl, S. Riedel, É. Gaussier, and
G. Bouchard.
Knowledge graph completion via complex tensor factorization.
arXiv preprint arXiv:1702.06879, 2017.
B. Yang, W.-t. Yih, X. He, J. Gao, and L. Deng.
Embedding entities and relations for learning and inference in
knowledge bases.
arXiv preprint arXiv:1412.6575, 2014.
16