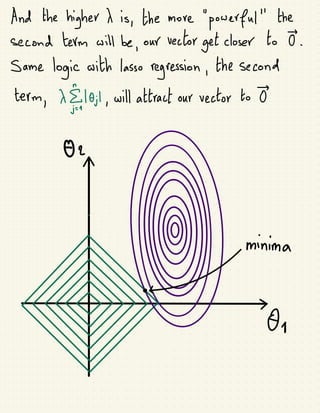
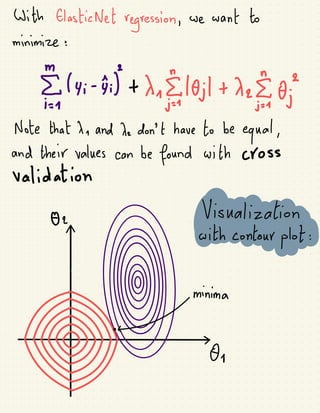
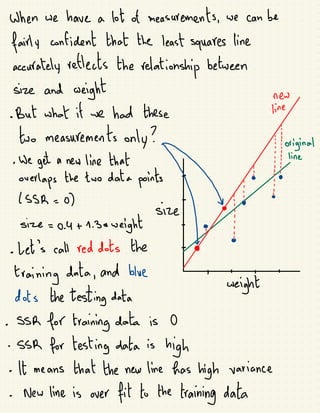
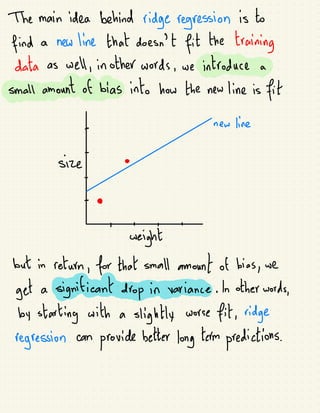
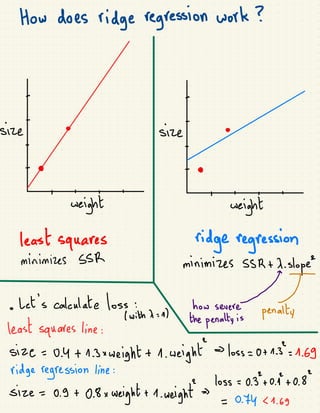
The document discusses various regularization techniques in machine learning, including ridge regression, lasso regression, and elastic net regression, which are used to minimize overfitting by introducing bias and reducing variance. Ridge regression improves predictions by penalizing the sum of squared residuals along with a term based on the slope, while lasso regression can completely eliminate irrelevant variables by shrinking their coefficients to zero. Elastic net regression combines the strengths of both ridge and lasso, allowing for the selection of the best regularization method based on the characteristics of the dataset.

1. Notes on
Regularization
in machine
learning
·
Ridge regression (Le
regularization)
·
Lasso
regression (LI
regularization)
· Elastic Net
regression

2. ·
Let's start
with data thatrepresents seights
and
sizes of
mice
predicted-
·
size
size ·
⑧
-
·
-
seight
of mouse shom
se sant
to predict
size
-
eight
Since these data look relatively linear,so
sill
use Linear Regression, ARA
least squares, to
model the
relationship between seight and size.
·
Ultimately, we end up
with this equation for the line:
size = 0.9 +
0.75*
seight
intercept slope

3. When we have a lot of measurements, we can be
fairly confident
that
the least squares line
accurately reflects the
relationship between
size and weight net
·
But
what
it se had these line
too measurements only?
!
·in
original
·
We get a new line that line
(SSR =
0)
·?.
.
craps are so date
positions.
size =
0.4 +
1.34 seight ⑤8.
·
Let's call red dots the -
⑨
training data, and blue
dots the testing data
.
SSR for training data is s
·
SSR for testing data is
high
· It means that
the new line has high saviance
·
Newline is over fitto the
training data

4. The main idea behind ridge regression is to
find a new line that
doesn't fit the training
data as sell, in other words, we introduce a
small amount
ofbias into how the new line is fit
nes line
-
size ⑧
-
-
-
eight
but in return, for thatsmall amountofbias, se
get a significantdrop in variance. In other words,
by starting with a
slightly sorse fit, ridge
regression can
provide better long term
predictions.

5. How does ridge regression sork?
-
-
size ⑧
size ⑧
-
-
- -
-
eight
-
eight
least
squares ridge regression
minimizes SSR minimizes
SSR+X.e
~
·
Let's calculate loss:
least
squares line:
litnx: epennes penalty
size =
0.4 +1.3x eight + 1. seight loss =
0 +
1.3°=
1.69
ridge regression line:
size =
0.9 +
8.8x seight +
1.seight loss
=
0.3 0.1+ 0.8°
= 0.74 <1.69

6. Thus, if we wanted to minimize the sum of the
squared residuals +
the
ridge regression penally,
we would choose the ridge regression line over the
least
squares line
Lambda(X):
Shen the slope of
the line is steep, then the prediction
for size is very sensitive to relatively small
changes in seight. And size versa, when the slope
is small, predictions for size are much less
sensitive to
ages
in
weight

7. -
-
size ⑧
size ⑧
-
-
- -
-
weight
-
eight
x =
8 x =
1
lequivalentto least
squares)
-
-
-
size ⑧
size ⑧
-
-
- -
-
eight
-
eight
X =
3 X =
1000

8. So the
larger x
gets, our predictions for size
become less and less sensitive to seight.
and the larger we make X, the slope gets
asymptotically close to 8
How do we decide the value of
X?
be
just
try a bunch of
values
for X
and use
cross validation, typically 10-fold C.J.,
to determine which one results in the losest
saviance.
Xc(0; +
0)
n the presious example, we're seen has
ridge
regression would work when predicting a
continuous
saviable, using a continuous variable. But
it
also works when using a discrete variable

9. Ridge regression can also be used for
logistic regression
doptimize the sum of
the likelihoods + X. Slope
So far, we're seen
examples
of
how
ridge
regression helps reduce saviance by
shrinking
parameters and
making predictions less sensitive
to them
We can also
apply ridge regression shen
we have more than 1
parameter
Example:
y =
be+
foxo+
feret---
be minimize:
loss -
Ely,ii) +
1
0;

10. Minimizing RSS +
18
8
(y -
x0)"(y -
x8) +
x0
y*y -
28xy +
8xx6 +
x8 8
because (X8)"= 8x*
&y-28x4 +
0x6 +
x0%
=
-
2X*y +
2xx8 +
8x8
68
set it
equal to 0, solve for 8
0 =
- 2xxy +
exx8 +
ex8
0 =
- x*y +
xx +
x8
x*y =
x
+
x6 +
x8
x*y =
(xx +
xI)8
(xx +
x])x*y =
0

11. Lass' regression:
Difference with ridge regression:
ridge regression:minimize SSR+Xx slope
lasso regression:minimize SSR
+Xx/slopel
They look similar, and they can be used in
similar situations
ND: Just
like with ridge regression, in lasso
regression, Xc(0,) and can be determined
using
cross solidation. And it
also
produces a line
with a littlebitof
bias but less saviance than
least squares
· With multiple parameters:
4 =
to +
0xxo+
fexet...
loss-
ly:-y,) +
18;1
j
=
x

12. So what's the difference?
Ridge regression can only shrink the slope
asymptotically close to 0, while lasso regression
can shrink the slope all the
way
to
8
· So, lasse
regression can exclude useless
saviables from equations, it is a little bit
better
than ridge regression
at
reducing the saviance
in models that
contain a
lot
of
useless variables.
in
retire
raniresen

13. Explanation with a contour plot:
withoutregularization, the goal is to minimize
lyi-yil only, the minima will be inside
the circles
⑧
*
minag.

14. But with ridge regression, there will be another
term, that
will "attract"parameters (here to, be)
to zero. So here our
algorithm will try to
minimize the sum of
too terms:
E(yi-xi), which attracts our rector to the center
of
purple circles, and x
E,8; shich attracts
our sector to 8:
So our minima will be somewhere in-between
⑦&
I ⑧ a
minima
-
Ex

15. And the higher X is, the more
"poserful"the
second term will be, our rector getcloser to 0.
Same
logic with lasso
regression, the second
term,
yl0j1,
will attractour sector to
↳
mina
=

16. Elastic Net
regression:
·
We said that lasso
regression works best when
your model contains a lotof useless variables
·
We also said thatridge regression works best
when most of
the variables are useful
·
Soil
we know a lot
about
all of the parameters
in our model, it's easy to choose
But what if we don't?
de use Elastic Net
regression
It combines both lasso
regression and
ridge regression, and takes advantage
of
both oftheir benefits

17. With Elastic Net
regression, we wantto
minimize:
(4i-yi) +
X, 18;1 +
xe,8;
j=
1
Note that
do and to don't
have to be
equal,
and their values can be foundwith cross
validation
⑦&
Visualization
with contour plot:
I · X
minima
⑧
-
Ex