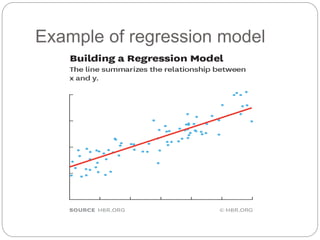
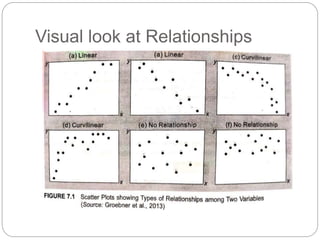
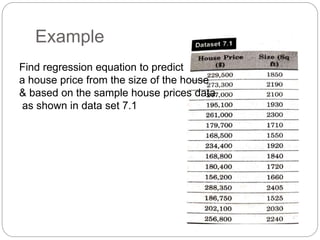
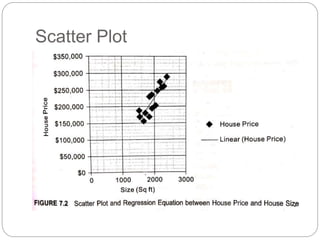
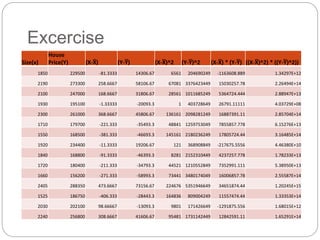
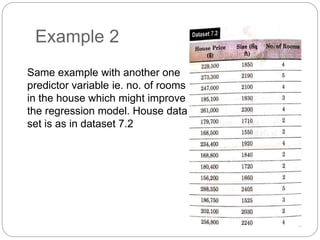
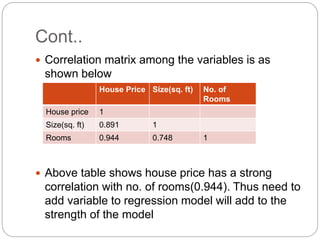
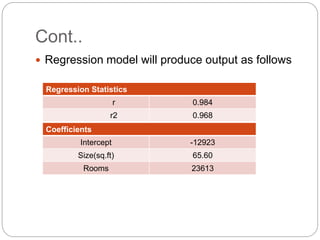
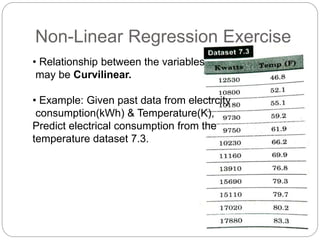
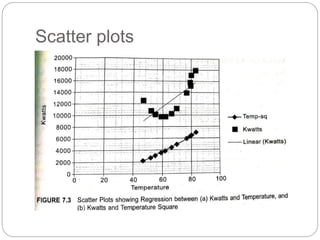
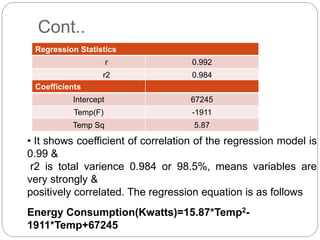
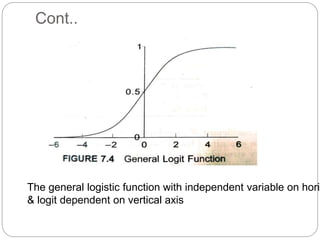
Regression is a statistical technique used to model relationships between variables. The key steps are to identify variables, select a dependent variable to predict, examine relationships visually, and find a way to predict the dependent variable using other variables. Correlation coefficients measure the strength of relationships between 0-1. Positive relationships have variables moving in the same direction, while negative relationships have them moving in opposite directions. Non-linear regression can model curvilinear relationships using quadratic terms. Logistic regression is used for categorical dependent variables.

1. Nandini V Patil
Asst.Professor
Godutai Engg. College Kalaburagi
Regression

2. Introduction
 Regression is a well-known statistical technique
to model the predictive relationship between
several independent variable & one dependent
variable.
 The objective is to find the best-fitting curve for a
dependent variable in multi dimensional space
with the each independent variable being a
dimension.
 The curve should be a straight line or nonlinear
curve.
 The quality of fit of the curve to the data can be
measured by coefficient of correlation(r) = √amt of
variance

3. Example of regression model

4. Conti
Key steps for regression:
1. List all the variables available for making the model.
2. Establish a dependent variable(DV) of interest.
3. Examine visual relationships between variables of
interest.
4. Find a way to predict DV using other variables.

5. Correlations and relationships
 Correlation coefficients are used to measure the
strength of the relationship between two variables.
 Correlation is a quantitative measure and it is
measured in the normalized range of 0 to 1.
 1  Perfect relationship means two variables are perfect
synchronized .
 0  No relationship between variables.
 Two types of relationships
o Positive: a relationship between two variables in
which both variables move in same direction.
o Negative orinverse relationship: a relationship
between two variables in which both variables
move in opposite direction.
 Correlation coefficient is
r= Σ(X-X̅) (Y-Y̅) / √(Σ(X-X̅ )2) * (Σ(Y-Y̅ )2))

6. Visual look at Relationships

7. Regression Exercise
 Regression model is described as a Linear
equation that have ‘y’ as dependent variable ie
variable being predicted & ‘x’ is the independent
variable ie predictor variable.
 Many independent variables & one dependent
variable in regression equation
 y = β0 + β1x + E
 Where β0 & β1 are constant and co-efficent for x variable
 E is a random error variable.

8. Example
Find regression equation to predict
a house price from the size of the house
& based on the sample house prices data
as shown in data set 7.1

9. Scatter Plot

10. Size(x)
House
Price(Y) (X-X̅) (Y-Y̅) (X-X̅)^2 (Y-Y̅)^2 (X-X̅) * (Y-Y̅) ((X-X̅)^2) * ((Y-Y̅)^2))
1850 229500 -81.3333 14306.67 6561 204690249 -1163608.889 1.34297E+12
2190 273300 258.6667 58106.67 67081 3376423449 15030257.78 2.26494E+14
2100 247000 168.6667 31806.67 28561 1011685249 5364724.444 2.88947E+13
1930 195100 -1.33333 -20093.3 1 403728649 26791.11111 4.03729E+08
2300 261000 368.6667 45806.67 136161 2098281249 16887391.11 2.85704E+14
1710 179700 -221.333 -35493.3 48841 1259753049 7855857.778 6.15276E+13
1550 168500 -381.333 -46693.3 145161 2180236249 17805724.44 3.16485E+14
1920 234400 -11.3333 19206.67 121 368908849 -217675.5556 4.46380E+10
1840 168800 -91.3333 -46393.3 8281 2152310449 4237257.778 1.78233E+13
1720 180400 -211.333 -34793.3 44521 1210552849 7352991.111 5.38950E+13
1660 156200 -271.333 -58993.3 73441 3480174049 16006857.78 2.55587E+14
2405 288350 473.6667 73156.67 224676 5351946649 34651874.44 1.20245E+15
1525 186750 -406.333 -28443.3 164836 809004249 11557474.44 1.33353E+14
2030 202100 98.66667 -13093.3 9801 171426649 -1291875.556 1.68015E+12
2240 256800 308.6667 41606.67 95481 1731142449 12842591.11 1.65291E+14
Excercise

11. Calculations of regression equations
 X̅ =Sum of values/total no. of values=28970/15=1931.333
 Y̅ = 3227900/15= 215193.333
 r= Σ(X-X̅) (Y-Y̅) / √(Σ(X-X̅ )2) * (Σ(Y-Y̅ )2))
 = 146946633.3 / √ 2.71918E+16
 = 146946633.3 / 164899238.1
 r = 0.89112985
β1 = r * sy/sx
= 0.891* 42937.050/ 274.320
= 139.4810276
β0 = Y̅ - β1 * X̅
= 215193.333 - 139.4810276 * 1931.333
= -54190.97848
≈ -54191

12. Cont..
 The regression model between two variable will
produce output as follow
Regression Statistics
r 0.891
r2 0.794
Coefficients
Intercept -54191
Size(sq.ft) 139.48

13. Cont..
 Correlation coefficient is 0.891. r2 is the measure of
total variance which is 0.794 or 79%. This shows that
two variables are moderately & positively correlated.
So regression equation will be (by filling values in the
above equation)
 Regression equation for two variables y and x is
y = β0 + β1x + E
House price ($)=139.48 * Size (Sq.ft) –
54191

14. Example 2
Same example with another one
predictor variable ie. no. of rooms
in the house which might improve
the regression model. House data
set is as in dataset 7.2

15. Cont..
 Correlation matrix among the variables is as
shown below
 Above table shows house price has a strong
correlation with no. of rooms(0.944). Thus need to
add variable to regression model will add to the
strength of the model
House Price Size(sq. ft) No. of
Rooms
House price 1
Size(sq. ft) 0.891 1
Rooms 0.944 0.748 1

16. Cont..
 Regression model will produce output as follows
Regression Statistics
r 0.984
r2 0.968
Coefficients
Intercept -12923
Size(sq.ft) 65.60
Rooms 23613

17. Cont..
 Correlation coefficient is 0.984. r2 is the measure
of total variance which is 0.968 or 97%. This
shows that two variables are positively and very
strong correlated. So adding new relevant
variable has helped to improve the strength of the
regression model. The regression equation is as
follows
House price ($)=65.6 * Size (Sq.ft)
+23613*Rooms+12924

18. Conti
 Predict the house price for the followings
 House price ($)=65.6 * 2000+ 23613*3+
12924
house price Size(sq.ft) #No. of Rooms
?? 2000 3

19. Non-Linear Regression Exercise
• Relationship between the variables
may be Curvilinear.
• Example: Given past data from electrcity
consumption(kWh) & Temperature(K),
Predict electrical consumption from the
temperature dataset 7.3.

20. Scatter plots

21. Cont…
 The relationship between temperature & Kwatts is
curvilinear model, which it hits bottom at a certain
value of temperature. The regression model
confirms the relationship, r = 0.77 & r2 is only
60%. Thus it gives only 60% variance.
 This regression model can be enhanced by
introducing nonlinear (quadratic variable temp2)in
the equation. The second line in scatter graph
shows relationship between kwh & temp2. the
graph shows energy consumption has a strong
linear relationship with temp2.

22. Cont..
Regression Statistics
r 0.992
r2 0.984
Coefficients
Intercept 67245
Temp(F) -1911
Temp Sq 5.87
• It shows coefficient of correlation of the regression model is
0.99 &
r2 is total varience 0.984 or 98.5%, means variables are
very strongly &
positively correlated. The regression equation is as follows
Energy Consumption(Kwatts)=15.87*Temp2-
1911*Temp+67245

23. Logistic Regression
 It works with dependent variables that have
categorical values.
 It measures relationship between a categorical
dependent variable & one or more independent
variables.
 eg: It is used to predict whether patient has a given
disease, based on observed characteristics of the
patient.
 Logistics regression model use probability scores as
the predicted values of the dependent variables.
 It takes the natural logarithm of the probability of the
dependent variable & creates a continuous criterion
as a transformed version of the dependent variable.
Thus logit transformation is used as dependent
variable.
 Dependent variable is binomial, logit is continuous
function upon which linear regression is conducted.

24. Cont..
The general logistic function with independent variable on horiz
& logit dependent on vertical axis

25. Advantages of Regression Model
 Regression models –
 Easy to understand because they built upon basic
statistical principles
 Simple algebraic equation’s which are easy to
understand.
 Easy to understand measuring terms which are
correlation coefficients & some other related
statistical parameters.
 Good predictive power than other models
 All variables can be included in the model.
 Tools are pervasive as they found in statistical
package as well as data mining package.

26. Disadvantages of Regression Model
 Regression models Can not work–
 cover poor quality data.
 Collinearity problems. If the independent variables
have strong correlation among themselves, then
they will eat into each other predictive power &
regression coefficients will lose their ruggedness.
 Unwieldy & unreliable if large no. of variables are
included in the model.
 On Nonlinear data automatically, user needs to be
added to improve its fit by imagine the kind of
additional terms.
 with categorical variables but only work on
numerical data,but can deal by creating multiple
new variables with yes or no.