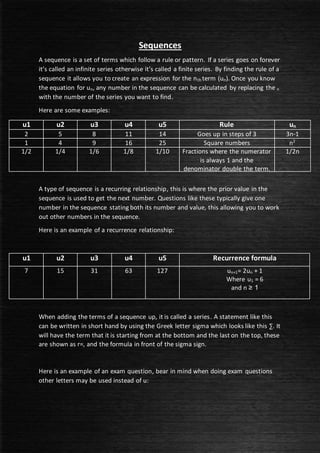
A sequence is a set of terms that follow a pattern or rule. If the sequence continues indefinitely, it is called an infinite sequence, otherwise it is finite. The rule allows you to write an expression for the nth term (un). Common examples include arithmetic sequences where the difference is constant, and geometric sequences where each term is obtained by multiplying the previous term by a fixed value. A recurrence relation defines each term in terms of the preceding ones. To solve problems involving sequences, you determine the expression for successive terms and find sums by adding terms up using the Greek letter sigma. Exam questions may involve finding individual terms, sums, or showing sums are divisible.

1. Sequences
A sequence is a set of terms which follow a rule or pattern. If a series goes on forever
it’s called an infinite series otherwise it’s called a finite series. By finding the rule of a
sequence it allows you to create an expression for the nth term (un). Once you know
the equation for un, any number in the sequence can be calculated by replacing the n
with the number of the series you want to find.
Here are some examples:
u1 u2 u3 u4 u5 Rule un
2 5 8 11 14 Goes up in steps of 3 3n-1
1 4 9 16 25 Square numbers n2
1/2 1/4 1/6 1/8 1/10 Fractions where the numerator
is always 1 and the
denominator double the term.
1/2n
A type of sequence is a recurring relationship, this is where the prior value in the
sequence is used to get the next number. Questions like these typically give one
number in the sequence stating both its number and value, this allowing you to work
out other numbers in the sequence.
Here is an example of a recurrence relationship:
u1 u2 u3 u4 u5 Recurrence formula
7 15 31 63 127 un+1= 2un + 1
Where u1 = 6
and n ≥ 1
When adding the terms of a sequence up, it is called a series. A statement like this
can be written in short hand by using the Greek letter sigma which looks like this ∑. It
will have the term that it is starting from at the bottom and the last on the top, these
are shown as r=, and the formula in front of the sigma sign.
Here is an example of an exam question, bear in mind when doing exam questions
other letters may be used instead of u:

2.  We are given an expression for a1 and the recurrence formula and also told k
is a positive integer.
 Part a says to write down an expression for a2. This can be done by inserting
the value given for a1 into the formula.
a1+1 = 5a1 + 3
a2 = 5(k) + 3
a2 = 5k + 3
 For part b it says show that a3 = 25k +18, we can do this by repeating what we
did for part a, only this time insert our value for a2 into the formula.
a2+1 = 5a2 + 3
a3 = 5(5k + 3) +3
a3 = 25k + 15 + 3
a3 = 25k + 18
 For part c i it wants us to find the sum of the series from the 1st
term to the 4th
term in its simplest form. First thing we have to do is work out what the 4th
term is by putting a3 into the formula to give an expression for a4.
a3+1 = 5a3 + 3
a4 = 5(25k + 18) + 3
a4 = 125k + 90 + 3
a4 = 125k + 93
 Now we can find the sum of the series from the 1st
term to the 4th
term by
adding all our calculated values up.
a1 + a2 + a3 + a4
= k + 5k + 3 + 25k + 18 + 125k + 93
= 156k + 114
 For c ii we have to show the sum can be divided by 6.
(156k + 114)/6
= 26k +19

3. Practise questions
1)
Answers
a) a1 = 2
b) 198
2)
Answers
a) a2 = 6k
b) k = -1/3 or k = -1

4. 3)
Answers
a) u3 = 17, u4 = 33
b) 64
4)
Answers
a) a2 =√7 , a3 = √10
b) 4