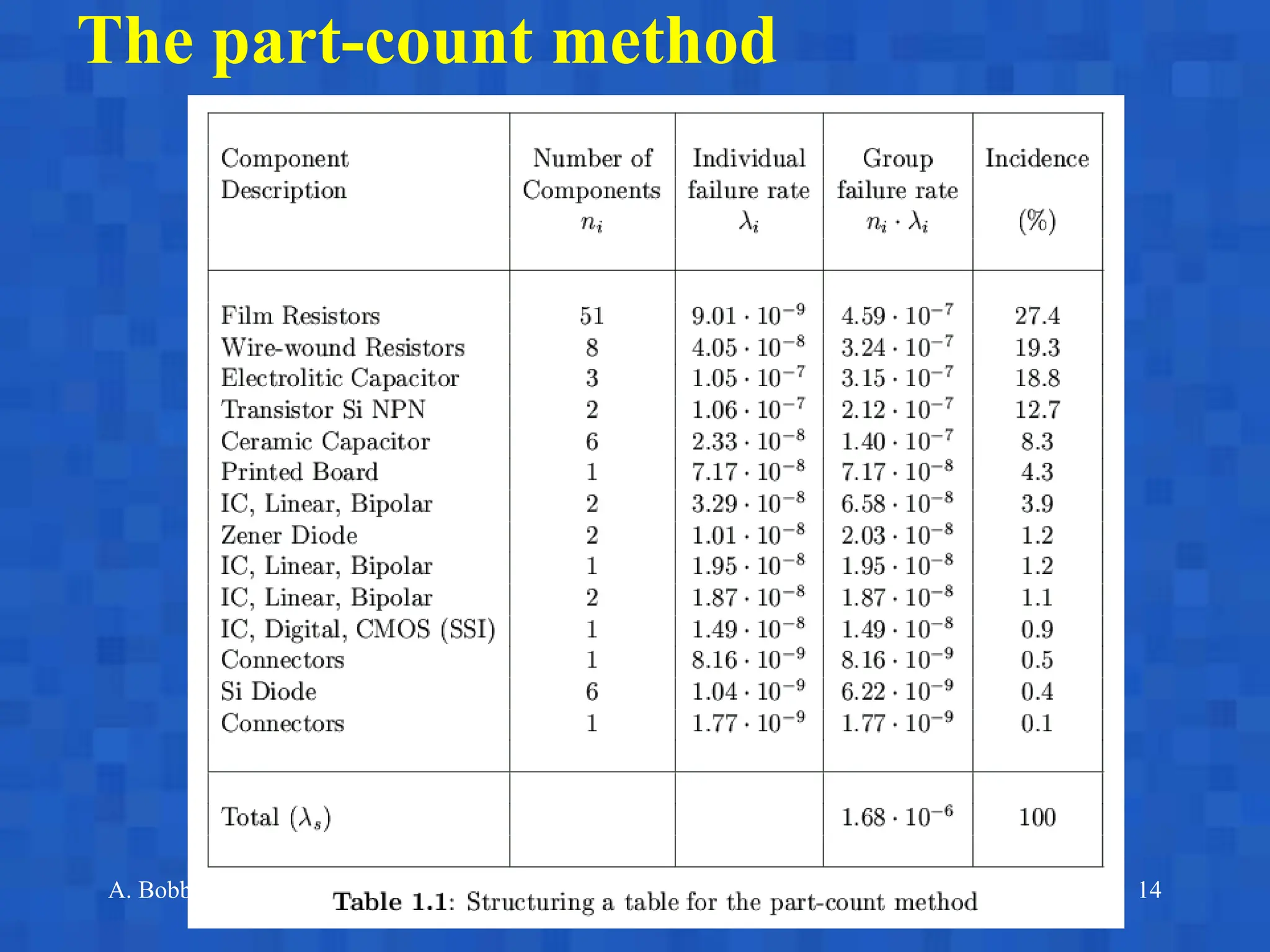
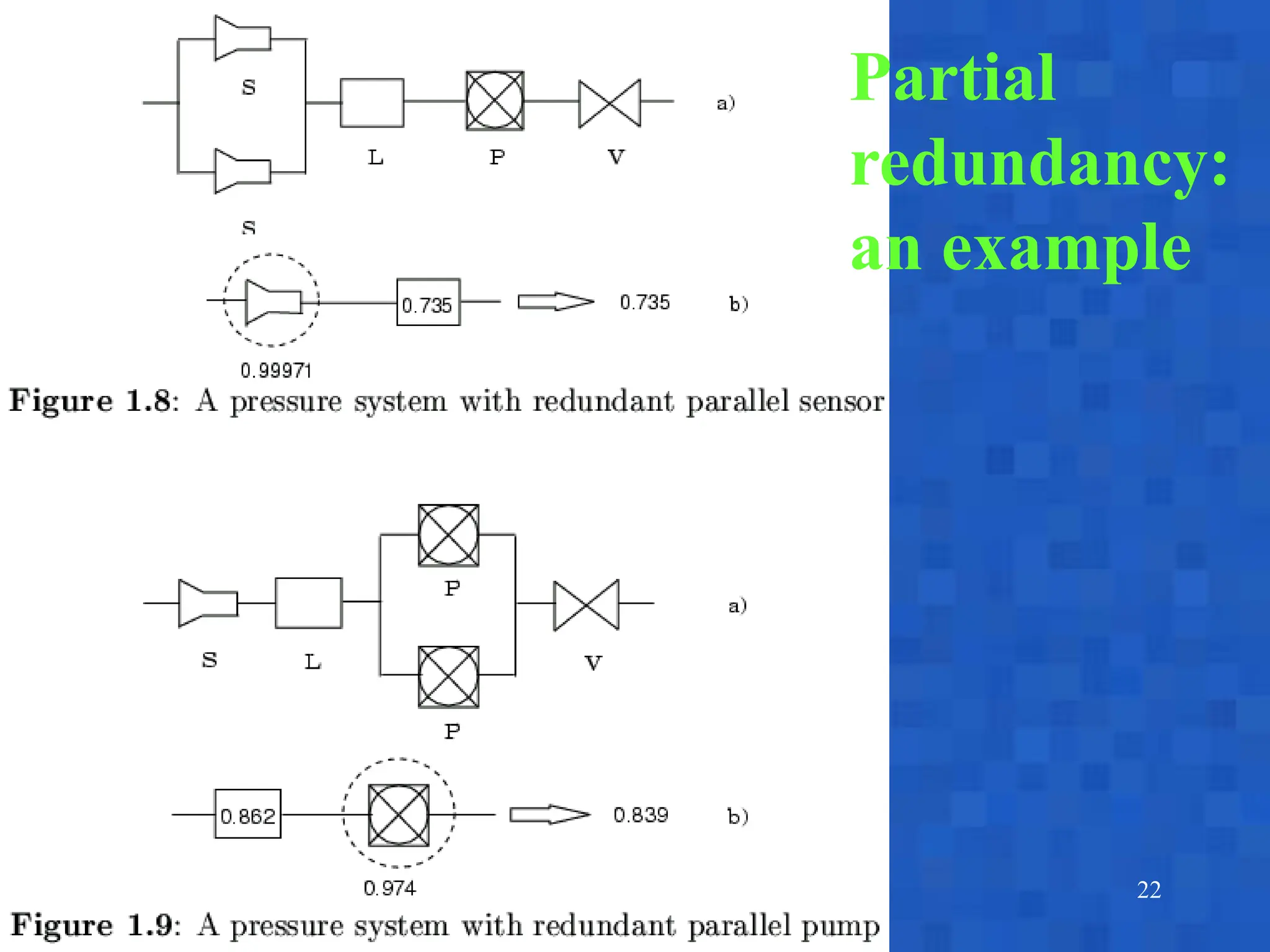
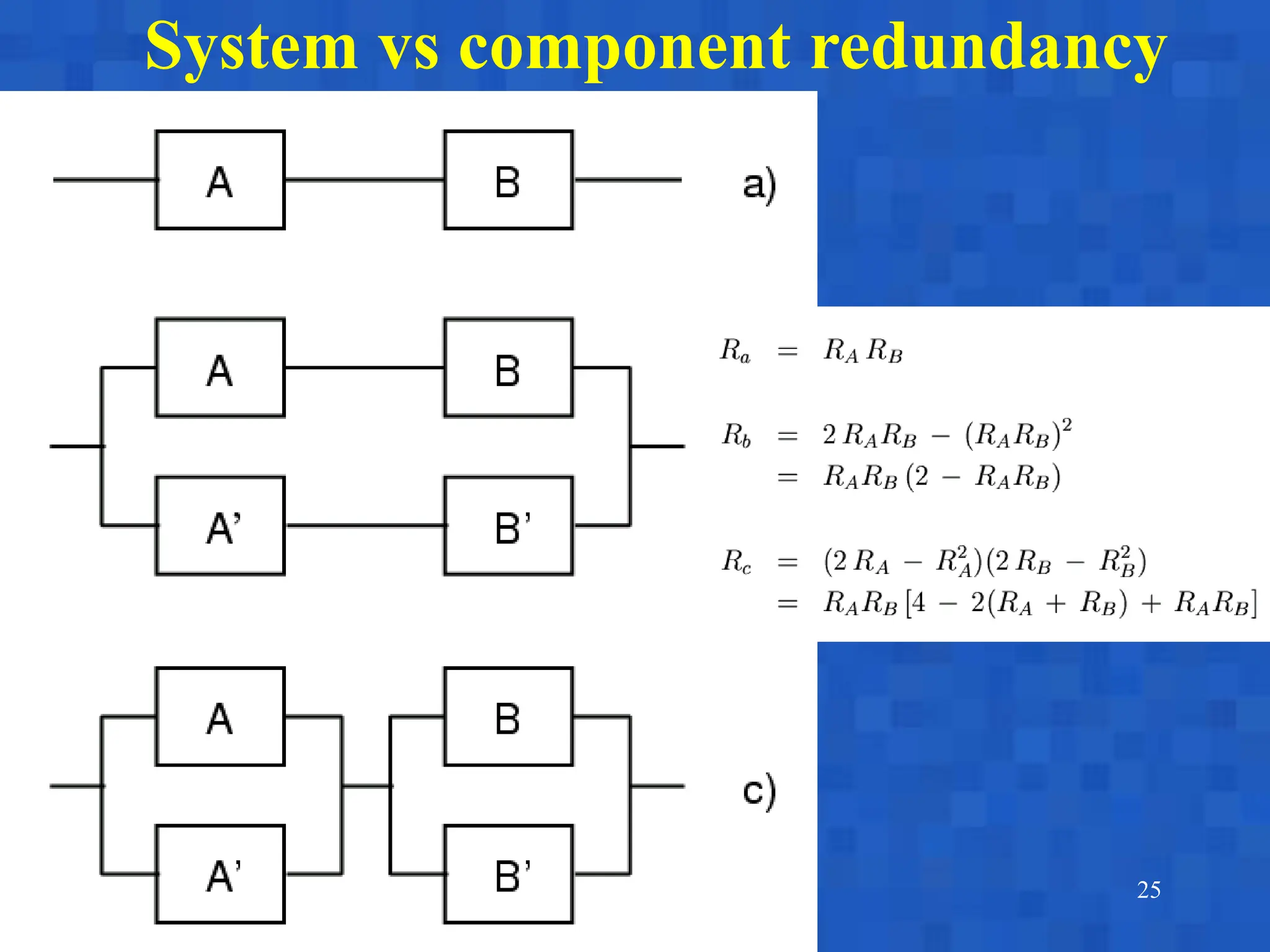
The document presented by Andrea Bobbio focuses on reliability block diagrams (RBDs) as a method to assess system dependability and maintainability. It discusses the modeling of components in series and parallel systems, highlighting the importance of statistical independence in failure analysis and introducing methods to calculate reliability and availability. Additionally, it addresses concepts such as redundancy, sensitivity analysis, and offers examples to illustrate the application of these methods.