An introdution to reliability and maintainability engineering 2nd ed Edition Ebeling
An introdution to reliability and maintainability engineering 2nd ed Edition Ebeling
An introdution to reliability and maintainability engineering 2nd ed Edition Ebeling






















![2 An Introduction to Reliability and Maintainability Engineering
coming apart from the main body of the tire. Because of the excessive number of
failures, Firestone was forced to recall 7.5 million tires. On November 8, 1940, the
Tacoma Narrows Bridge, five months old, collapsed into Puget Sound from vibra-
tions caused by high winds. Metal fatigue induced by several months of oscillations
led to the failure. The Manus River bridge (Greenwich, Connecticut) collapsed in
1983, killing three people and injuring three. While there is disagreement on the
cause of the disaster, blame has been placed on the original design, on corrosion that
had caused undetected displacement of the pin-and-hanger suspension assembly, on
poor maintenance, and on inadequate inspections. The Hartford (Connecticut) Civic
Center Coliseum roof collapsed in 1978 from structural failure due to the weight of
the snow and ice accumulated on the roof. A major shortcoming in the roof frame
system was the lack of redundancy of members to carry loads when other individual
members failed. An inadequate safety margin may also have contributed. The Three
Mile Island disaster in 1979, which resulted in a partial meltdown of a nuclear reac-
tor, was a result ofboth mechanical and human error. When a backup cooling system
was down for routine maintenance, air cut off the flow ofcooling water to the reactor.
Warning lights were hidden by maintenance tags. An emergency relief valve failed
to close, causing additional water to be lost from the cooling system. Operators were
either reading gauges that were not working properly or taking the wrong actions
on the basis of those that were operating. The 1986 explosion of the space shuttle
Challenger was a result of the failure of the rubber O-rings that were used to seal
the four sections of the booster rockets. The below-freezing temperatures before the
launch contributed to the failure by making the rubber brittle.!
From the above examples one can conclude that the impact of product and sys-
tem failures varies from minor inconvenience and costs to personal injury, signif-
icant economic loss, and death. Causes of these failures include bad engineering
design, faulty construction or manufacturing processes, human error, poor mainte-
nance, inadequate testing and inspection, improper use, and lack ofprotection against
excessive environmental stress. Under current laws and recent court decisions, the
manufacturer can be held liable for failing to account properly for product safety
and reliability. Engineers responsible for product design must therefore include both
reliability and maintainability as design criteria. The objective of this text is to intro-
duce the technical manager and the engineer to the concepts, models, and analysis
techniques that form the basis of reliability and maintainability engineering.
This, then, is a book on the failure and repair characteristics ofsystems, products,
and their component parts. Reliability and maintainability engineering attempts to
study, characterize, measure, and analyze the failure and repair ofsystems in order to
improve their operational use by increasing their design life, eliminating or reducing
the likelihood of failures and safety risks, and reducing downtime, thereby increas-
ing available operating time. Closely associated with reliability and maintainability
for systems or components that can be repaired or restored to an operating state once
they have failed is the concept of availability. Availability measures the combined
I Details ofthese and other disasters may be found in the highly interesting book When Technology Fails
[Schlager, 1994].](https://image.slidesharecdn.com/60222-250303060215-7ac13b08/75/An-introdution-to-reliability-and-maintainability-engineering-2nd-ed-Edition-Ebeling-23-2048.jpg)




![CHAFfER 1: Introduction 7
TABLE 1.2
Reliability test data results
Motor
1-100 101-200 201-300 301-400 401-500 Total
Number tested 12
Hours on test 2540
Number failed 1
Failure rate 0.000394
1.3
APPLICATIONS
11 12
2714 2291
0 1
0 0.000436
12 15 62
1890 2438 11873
5 7 14
0.002646 0.002871 0.001179
The types of problems solved through the use of reliability and maintainability con-
cepts are illustrated by the following examples.
EXAMPLE 1.1. The B. A. Miller Company manufactures small motors for use in house-
hold appliances such as washing machines, dryers, refrigerators, and vacuum cleaners.
It has recently designed a new motor that has experienced the abnormally high failure
rate of 43 failures among the first 1000 motors produced. Several of these failures were
observed during final product testing by the appliance manufacturer. These motors were
inspected, and it appeared that the bearing case was turning in its seat. The sealed ball
bearings, however, appeared to be okay. Possible causes of these failures included faulty
design, defective material, and a manufacturing (tolerance) problem. The company initi-
ated an aggressive program of accelerated life testing of motors randomly selected from
the production line. As a result of the testing program, it observed that those motors pro-
duced near the end of a production run were failing at a higher rate than those at the start
of the run. Table 1.2 summarizes the results of the testing program, which are displayed
graphically in Fig. 1.1.
The failure rate is computed by dividing the number of failures by the total num-
ber of hours on test. Dividing total hours on test by the number of failures provides an
0.0030
.... 0.0025
] 0.0020
....
<I)
c.. 0.0015
'"
!:l
.a
'<a
0.0010
~
0.0005
0
1-100
FIGURE 1.1
Failure rates of motors.
101-200 201-300 301-400 401-500 Touu
Production number](https://image.slidesharecdn.com/60222-250303060215-7ac13b08/75/An-introdution-to-reliability-and-maintainability-engineering-2nd-ed-Edition-Ebeling-28-2048.jpg)
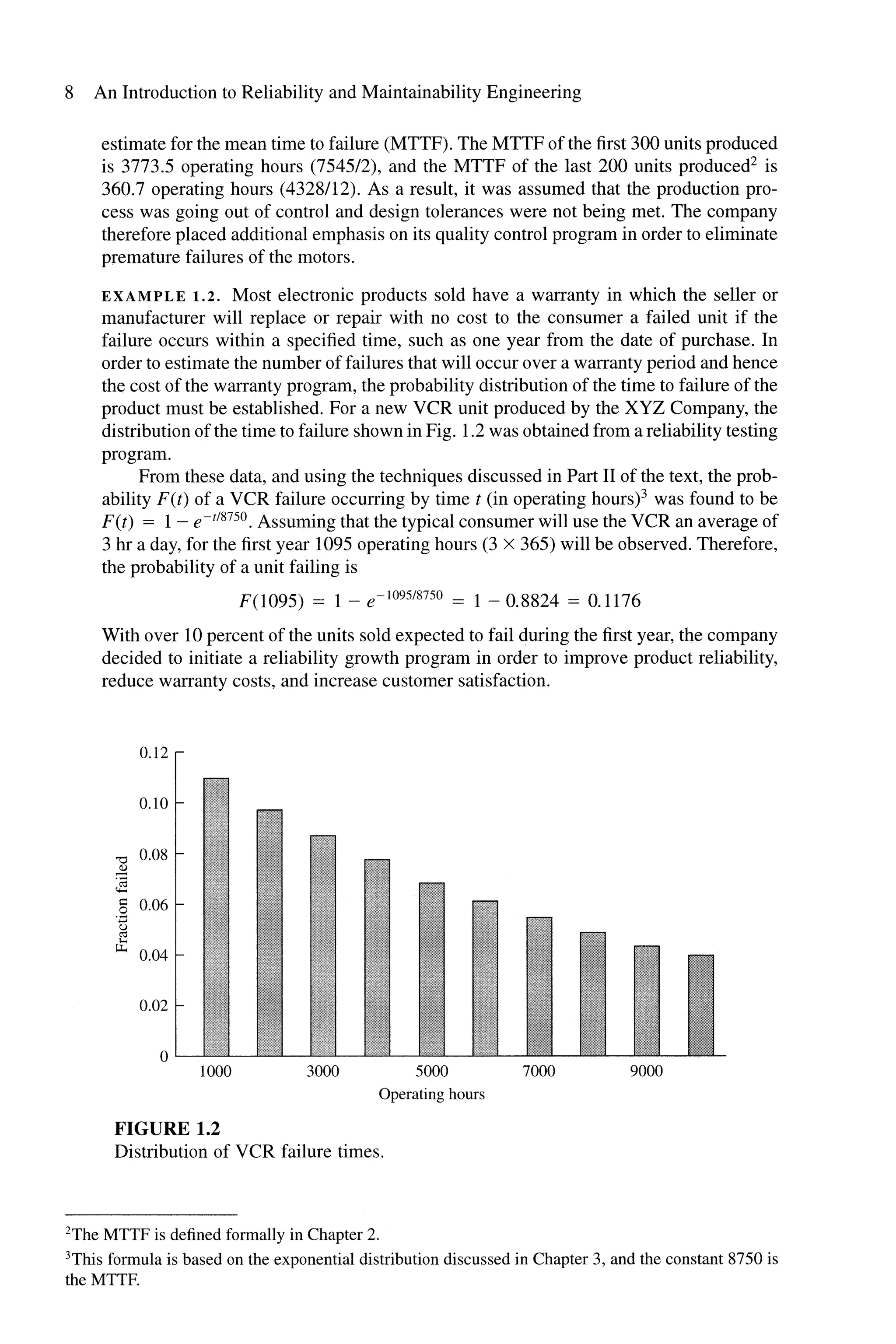
![CHAPTER 1: Introduction 9
EXAMPLE 1.3. A continuous-flow production line requires a product to be processed
sequentially on 10 different machines. When a machine breaks down, the entire line
must be stopped until the failure is repaired. The average downtime of the line is 12 hr.
This includes time spent waiting for parts and maintenance personnel as well as time
spent troubleshooting and fixing the failed machine. Machine specifications require a
0.99 reliability for each machine over an 8-hr production run. Therefore the reliability of
the production line over an 8-hr run is 0.9910 = 90 percent.4 Assuming a constant failure
rate (exponential failure distribution), this is equivalent to a mean time between failures
(MTBF) of 75.9 operating hours, found by solving the following for MTBF: R(8) =
e-8IMTBF = 0.90, where R(8) is the production line reliability over an 8-hr period.
Under fairly general conditions the steady-state availability of a system is given by
MTBF
A = MTBF + MTTR
where MTTR = the mean time to repair. Therefore, the steady-state availability of the
production line is currently 75.9/(75.9 +12) = 0.86. In order to meet production quotas,
the line must maintain at least a 0.92 availability. Since improvements in machine reli-
ability above 0.99 did not appear feasible, the company decided to increase availability
by improving the maintainability (i.e., decreasing the MTTR).
A minimum MTTR is obtained from Fig. 1.3 or by solving the availability formula
75.9/(75.9 + x) = 0.92 for x: x = 6.6 hr.
By hiring an additional maintenance person, increasing machine spare parts inven-
tory, relocating the inventory closer to the production line, improving diagnostic pro-
cedures, and simplifying the removal and replacement of high-failure components, the
company was able to reduce the MTTR to under 6 hr and achieve the desired availability
goal.
.:s
:g
1.00
0.95
~ 0.90
~
~
>, 0.85
]
CIl
0.80
6.6
0.75 L---'_---'-_--'--_-'-_--'--'-.L.-_L---'_---'-_--'--_-'-_--'----'
1 2 3 4 5 6 7 8 9 10 11 12 13 14
Mean time to repair
FIGURE 1.3
Availability of the production line.
4The logic of computing a system reliability for serial units is discussed in Chapter 5.](https://image.slidesharecdn.com/60222-250303060215-7ac13b08/75/An-introdution-to-reliability-and-maintainability-engineering-2nd-ed-Edition-Ebeling-30-2048.jpg)
![10 An Introduction to Reliability and Maintainability Engineering
1.4
A BRIEF HISTORY
Early foundations of reliability5 may be found in actuarial concepts used in the
insurance industry, particularly in the study of human survival probabilities. In
the late 1930s and 1940s Weibull analyzed fatigue life in materials, leading to
the probability distribution bearing his name. The study of structural reliability
and fatigue failure began in the 1930s and has since continued. Although early
(l930s and 1940s) development in such areas as queuing and renewal theory,
particularly with the use of the exponential distribution, provided some of the
mathematical foundations of reliability, it was not until after World War II that
reliability became a subject of study. This came about because of the relatively
complex electronic equipment used during the war and the rather high failure
rates observed. In particular, vacuum tubes were notoriously unreliable.
Following the war, Aeronautical Radio, Inc. (ARINC) was established by
commercial airlines to improve airborne electronic equipment (referred to as
avionics by the military). In 1950 the U.S. Air Force formed an ad hoc group to
improve general equipment reliability, and in 1952 the Defense Department
established the Advisory Group on Reliability of Electronic Equipment
(AGREE). The requirement of reliability testing and demonstration of new
systems emerged from this advisory group.
Work published during the 1950s centered around the use of the exponential
distribution to represent failure times, although interest in and the importance of
the Weibull distribution increased by the end of the decade. Initial textbooks on
reliability include Bazovsky [1961] and Barlow and Proschan [1967]. These were
followed by Smith [1976] and Kapur and Lamberson [1977]; the latter book is
still popular today. During the 1970s focus shifted to fault tree analysis, largely
because of concern about nuclear reactor safety. Progressing into the 1980s,
reliability networks received considerable attention in the literature. Both
reliability and maintainability received renewed emphasis in the mid-1980s with
the introduction of the Air Force's Reliability and Maintainability (R&M) 2000
program. Objectives of the R&M 2000 program were to increase system
readiness and availability and to reduce maintenance personnel requirements and
life-cycle costs through increased reliability and maintainability by the year 2000.
Since the turn of the century, much of the research in reliability has
transitioned from the military to industry and academia. This is particularly true
with regard to automotive manufacturers and their suppliers, who have had to
compete in the world market with increasingly reliable vehicles. To participate in
a global economy, companies must consider product reliability as a primary
concern. More universities are teaching reliability and faculty research and
publications on reliability have seen steady growth. Perhaps the most significant
development in reliability research has been the increased availability of
reliability data in electronic format. Today, there is little reason for a company
5Students interested in more detail about the development ofreliability are encouraged to read "Mathematical
Theory of Reliability: A Historical Perspective,'· by Barlow [1984].](https://image.slidesharecdn.com/60222-250303060215-7ac13b08/75/An-introdution-to-reliability-and-maintainability-engineering-2nd-ed-Edition-Ebeling-31-2048.jpg)

![CHAPTER 1: Introduction 13
be selected from among those models discussed in Part I. This requires
estimation of the distribution parameters, discussed in Chapter 15, and a
statistical goodness-of-fit test, discussed in Chapter 16, to either reject or not
reject the hypothesized distribution. From the material presented in Part II, the
reliability engineer should be able to establish a test plan, collect failure or repair
data, and complete a statistical analysis of the data, resulting in an acceptable
Part III, "Application," concludes the development of reliability engineering
by presenting several applications in Chapter 17 and by identifying policies,
procedures, issues, and concerns in implementing a reliability program in
Chapter 18. Together, these last two chapters attempt to integrate the material
from Parts I and II.
Other introductory texts on reliability include Bain and Engelhardt [1991],
Blanks [1992], Bunday [1991], Crowder et al. [1991], Dai and Wang [1992],
Elsayed [1996], Grosh [1989], Kales [1998], Kececioglu [1991], Leemis [1995],
Ramakumar [1993], Rao [1992], Sundararajan [1991], Todinov [2005], and
Zacks [1992].
APPENDIX IA
A PROBABILITY PRIMER
There are two general approaches to modeling uncertainty by using probability con-
cepts. The more basic method makes use of the idea of a sample space and events
defined over the sample space. It then defines the probability of these events and
computes probabilities of more complex events formed from unions and intersec-
tions of elementary events. The second method is based on the concept of a random
variable and a probability distribution associated with the random variable. A ran-
dom variable is a variable that takes on certain values in accordance with specified
probabilities. By specifying the probability distribution of a random variable, we can
completely characterize the random process. We will have occasion throughout this
text to utilize both methods. For example, we may define an event to be a component
failure and a random variable to be the time to failure of the same component.
IA.I
RANDOM EVENTS
In reliability engineering a failure can be described as a random event. A random
event E will occur with some probability denoted by peE) where 0 :s; peE) :s; 1.
peE) = 0 describes an impossible event, and peE) = 1denotes a certain event. The
closer peE) is to 1, the more likely it is that the event (e.g., failure) will occur.](https://image.slidesharecdn.com/60222-250303060215-7ac13b08/75/An-introdution-to-reliability-and-maintainability-engineering-2nd-ed-Edition-Ebeling-34-2048.jpg)


![16 An Introduction to Reliability and Maintainability Engineering
1 - 0.005 = 0.995, which is the probability that at least one ofthe two components does
not fail.
lA.2
BAYES' FORMULA
Bayes' formula involves conditional probabilities of two events. It can be derived
by observing that
p(AnB) p(BnA)
peA IB) = PCB) = P[(B n A) U (B n N)]
PCB IA)P(A)
PCB IA)P(A) + PCB IN)P(AC)
where the events B n A and B n AC are mutually exclusive.
(LlO)
EXAMPLE lA.6. A smoke detector is routinely inspected. Eighty percent of the detec-
tors found inoperative had experienced a power surge, and 10 percent of those found
in operating condition had experienced a power surge. Twenty percent of the detectors
inspected have failed. What is the probability of a detector failing given it experiences
a power surge?
Solution. LetA = the event that a detector has failed and B = the event that the detector
had experienced a power surge. Then peA) = 0.20, PCB IA) = 0.80, and PCB IAC) =
0.10. Therefore
peA IB) (0.80)(0.20) = 0.16 = 0667
= (0.80)(0.20) + (0.10)(0.80) 0.24 .
Bayes' formula is generalized as follows:
i = 1, ... , n (1.11)
where the events Ai, i = 1, ... , n, form a partition. That is, they are mutually exclu-
sive and their intersection comprises the entire sample space (they are collectively
exhaustive). As a result the denominator in Eq. (1.11) is equal to P(B).
lA.3
RANDOM VARIABLES
Although the concept of a random event is a useful one in describing random pro-
cesses, a more useful concept is that of a random variable. A random variable is a
variable that takes on numerical values in accordance with some probability dis-
tribution. Random variables may be either continuous (taking on real numbers)
or discrete (usually taking on nonnegative integer values). The probability dis-](https://image.slidesharecdn.com/60222-250303060215-7ac13b08/75/An-introdution-to-reliability-and-maintainability-engineering-2nd-ed-Edition-Ebeling-37-2048.jpg)


![CHAPTER 1: Introduction 19
lA.7
CONTINUOUS DISTRIBUTIONS
The following relations hold for any continuous probability distribution:
1. 0 :5 F(x) :5 1
x
2. Pr{X :5 x} = F(x) = If({) d{
3. f(x) = d~~x)
00
4. I f(x)dx = 1
-00
b
5. Pr{a:5 X :5 b} = If(x)dx = F(b) - F(a)
a
00
6. E(X) = JL = Ixf(x)dx
-00
where JL is the mean or expected value of the random variable X.
00
7. Var(X) = u 2 = I(x - JL)2 f(x)dx
where u 2 is the variance of the distribution.
(1.17)
(1.18)
(1.19)
(1.20)
(1.21)
(1.22)
8. If Y = L.7=1 aiXi where the Xi are independent random variables having means
JLi and variances uf and the ai are constants, then
n
E(Y) = 2:aiJLi
i= 1
and
n
Var(Y) = 2:afuf (1.23)
i= 1
In general we may describe the distribution of a random variable in terms of its
PDF, f(x), or its CDF, F(x). Although a random variable may be defined over the
open interval (-00,00), when the random variable represents a failure time or repair
time, only nonnegative values are permitted. Therefore the domain of the random
variable would normally be [0, 00), and the lower limits of the integrals in relations
2, 4, 6, and 7 would reflect this change. The concepts ofrandom variables and proba-
bility distributions are explored more fully in the next several chapters as the failure
probability distribution is developed as the primary focus ofPart I. Examples ofthese
distributions will therefore be presented in the context of their use in developing re-
liability models. More detailed coverage of probability theory may be found in Ross
[1987].](https://image.slidesharecdn.com/60222-250303060215-7ac13b08/75/An-introdution-to-reliability-and-maintainability-engineering-2nd-ed-Edition-Ebeling-40-2048.jpg)





![26 PART I: Basic Reliability Models
A design life is defined to be the time to failure tR that corresponds to a specified reliabil-
ity R. That is R(tR) = R. To find the design life if a reliability of 0.95 is desired, we set
1
R(t ) = 0.95
R O.OOltR +1
Solving for tct,
tR =1000(0.~5 -1)= 52.6hr
The probability of a failure occurring within some interval of time [a, b] may be
found using any of the three probability functions, since
Pr{ a :::; T :::; b} = F(b) - F(a) = R(a) - R(b) = rf(t)dt (2.6)
From the previous example,
1 1
Pr{ 10 :::; T :::; 100} = R(10) - R(100) = 0.01 + 1 - 0.1 + 1 = 0.081
2.2
MEAN TIME TO FAILURE
The mean time to failure (MTTF) is defined by
MTTF = E(T) = fo'''' tf(t)dt (2.7)
which is the mean, or expected value, of the probability distribution defined by f(t).
It can also be shown (Appendix 2A) that
MTTF = fo'''' R(t) dt (2.8)
Equation (2.8) is often easier to apply than (2.7).
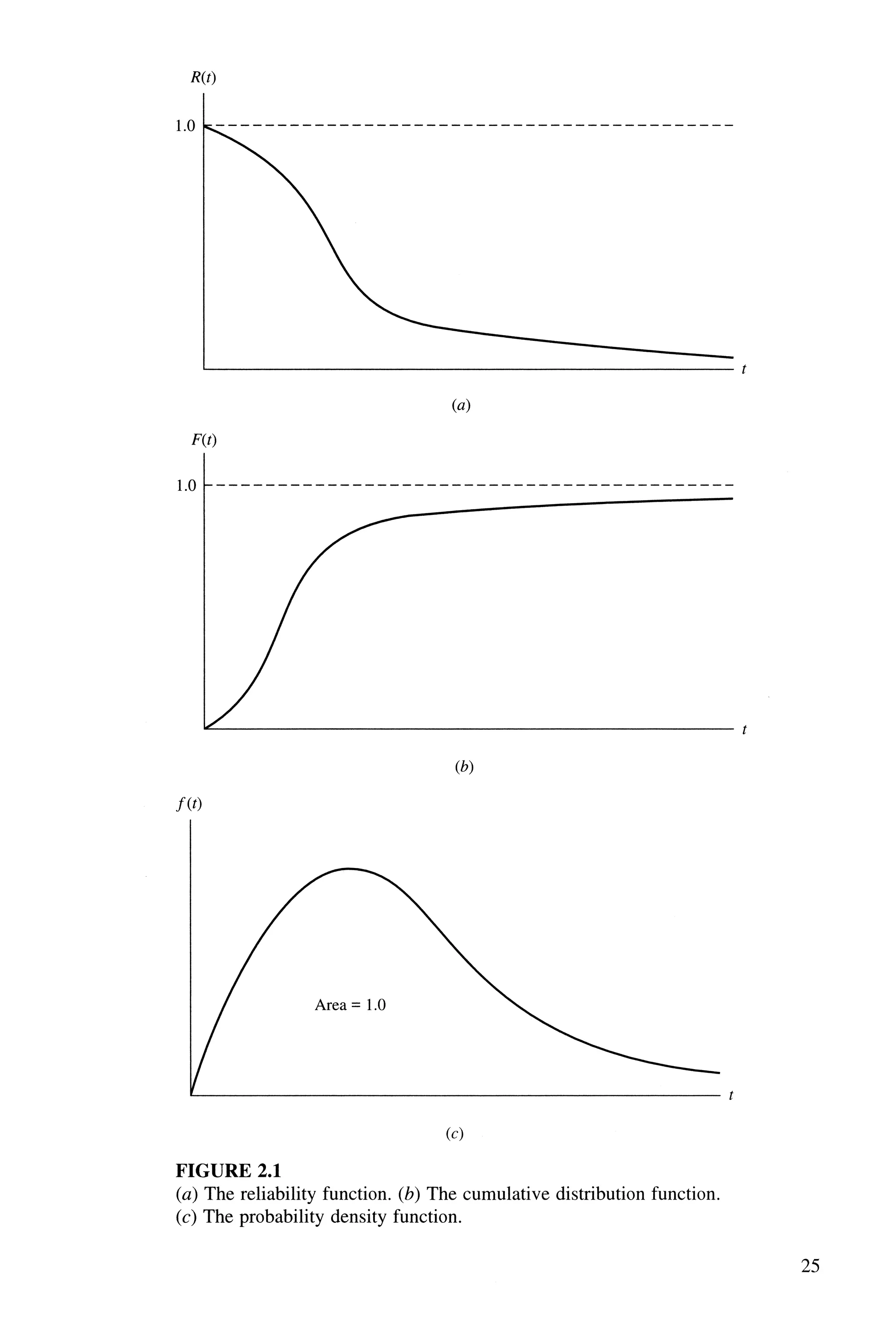
The mean of the failure distribution is only one of several measures of central
tendency of the failure distribution. Another is the median time to failure, defined by
R(tmed) = 0.5 = Pr{ T 2: tmed} (2.9)
The median divides the distribution into two halves, with 50 percent of the fail-
ures occurring before the median time to failure and 50 percent occurring after the
median. The median may be preferred to the mean when the distribution is highly
skewed.
A third frequently used average is the mode, or most likely observed failure
time, defined by
f(tmode) = max f(t)
O:s«oo
(2.10)
For a small fixed interval of time centered around the mode, the probability offailure
will generally be greater than for an interval of the same size located elsewhere
within the distribution. Figure 2.2 shows the locations of the mean, the median, and
the mode for a distribution skewed to the right.](https://image.slidesharecdn.com/60222-250303060215-7ac13b08/75/An-introdution-to-reliability-and-maintainability-engineering-2nd-ed-Edition-Ebeling-47-2048.jpg)

![Then
CHAPTER 2: The Failure Distribution 29
Pr{t :::; T :::; t + !It IT;::: t} = _R-,-(t,---)---=-R-,-:,(t_+_L1....:...t)
R(t)
R(t) - R(t + L1t)
R(t) L1t
is the conditional probability of failure per unit of time (failure rate).
Set
A(t) = lim -[R(t + L1t) - R(t)] . _1_
~t-+O !It R(t)
-dR(t) 1 f(t)
-----:d:--t:....:... . -R(-t) = -R(-t)
(2.13)
Then A(t) is known as the instantaneous hazard rate or failure rate function. The
failure rate function A(t) provides an alternative way of describing a failure distribu-
tion. Failure rates in some cases may be characterized as increasing (IFR), decreas-
ing (DFR), or constant (CFR) when A(t) is an increasing, decreasing, or constant
function.
A particular hazard rate function will uniquely determine a reliability function.
To see this, let
A(t) = -dR(t) . _1_
dt R(t)
or ( )d = -dR(t)
1 t t R(t)
Integrating,
(t , , _ IR(t) -dR(t')
Jo A(t ) dt - 1 R(t')
where R(O) = 1 establishes the lower limit in the integral on the right-hand side.
Then
-I:A(t') dt' = In R(t)
or R(t) = exp [- I:A(t')dt'] (2.14)
Equation (2.14) can then be used to derive the reliability function from a known
hazard rate function.
EXAMPLE 2.5. Given the linear hazard rate function A(t) = 5 x 1O-6t where t is mea-
sured in operating hours, what is the design life if a 0.98 reliability is desired?
Solution](https://image.slidesharecdn.com/60222-250303060215-7ac13b08/75/An-introdution-to-reliability-and-maintainability-engineering-2nd-ed-Edition-Ebeling-50-2048.jpg)





























