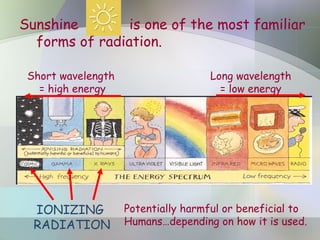
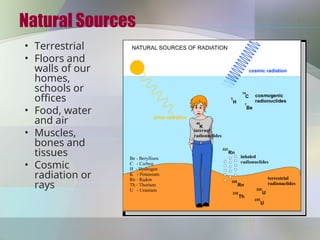
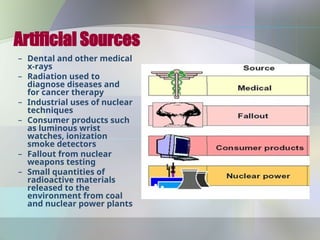
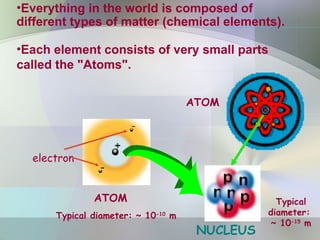
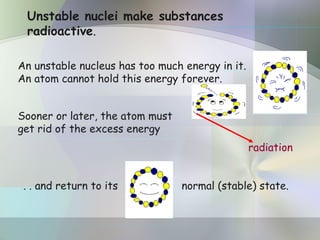
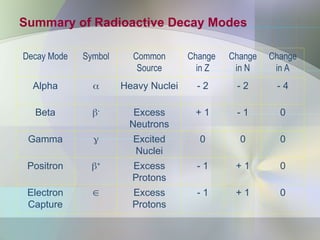
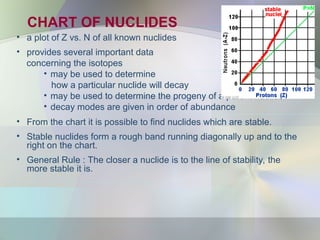
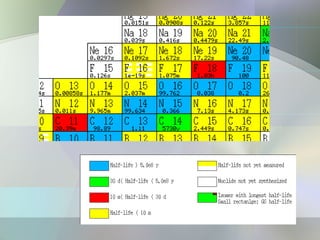
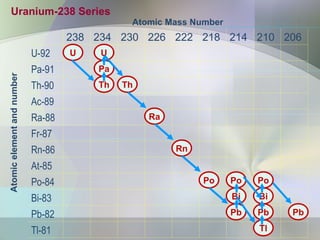
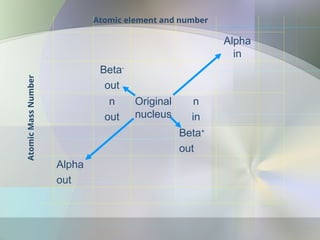
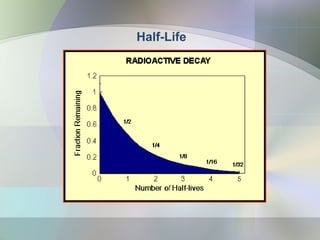
The document provides an overview of radioactivity, describing various types of radiation, their sources, and the process of radioactive decay. It explains the differences between ionizing and non-ionizing radiation, as well as the types of decay (alpha, beta, gamma) and related concepts such as half-life and decay chains. Additionally, it discusses the practical applications of radiation in medicine, industry, and research, highlighting the importance and prevalence of radiation in everyday life.

1. RADIOACTIVITY
and
RADIOACTIVE DECAY
REYNALDO S. JIMENEZ
Nuclear Training Center
Philippine Nuclear Research Institute

2. What is RADIATION ?
Has been around since the
earth was formed 4500
million years ago.
Can be detected, measured
and controlled.
87% of radiation dose
comes from natural sources,
e.g... cosmic, food we eat,
our homes
13% result of man’s activities..
- Medical Applications
(diagnosis and treatment of
disease)
- Industrial application
(inspection of welds, detection
of cracks in or cast metal)
- Research application (dating
of antiquities, food
preservation)

3. Radiation – any form energy that
travels and dissipates.
Ionizing Radiation – Its interaction with matter
may result to creation of charged particles.
Non-Ionizing Radiation – its interaction with
matter will not result to creation of charged
particles.

4. Everything in nature,
every creature
and every material
contains, and
always has contained,
radioactive
substances.
You are radioactive
yourself,
and so is your dog,
your coffee,
your seatmate,
and your mother-in-law.
Radiation is all around us.

5. Sunshine is one of the most familiar
forms of radiation.
IONIZING
RADIATION
Potentially harmful or beneficial to
Humans…depending on how it is used.
Short wavelength
= high energy
Long wavelength
= low energy

6. What is IONIZING RADIATION?
- the kind of radiation which is a result of the radioactive
process
- that which changes the physical state of atoms which it
strikes causing them to be electrically charged or
“ionized”
e-
Neutral atom
e-
e-
Ionized atom

7. SOURCES OF RADIOACTIVITY
Natural Sources
Artificial (Man-made)
accounts for 15% of the total
radiation burden
97% of man-made
radiation is due
to diagnostic medical exposures

8. Natural Sources
• Terrestrial
• Floors and
walls of our
homes,
schools or
offices
• Food, water
and air
• Muscles,
bones and
tissues
• Cosmic
radiation or
rays

9. Background Radiation
• Value of background
radiation is not stable, may
vary widely from place to place
and from time to time,
depending, for instance, on the
structure and wetness of the
soil, the seasons, changes in
weather, wind direction and
the level above sea
• Radiation emitted from
natural radioactive substances
in our environment and from
the cosmos

10. Artificial Sources
– Dental and other medical
x-rays
– Radiation used to
diagnose diseases and
for cancer therapy
– Industrial uses of nuclear
techniques
– Consumer products such
as luminous wrist
watches, ionization
smoke detectors
– Fallout from nuclear
weapons testing
– Small quantities of
radioactive materials
released to the
environment from coal
and nuclear power plants

11. What is RADIOACTIVITY ?
RADIOACTIVTY
is the process by
which certain atoms
spontaneously emit
high energy particles
or rays from their
nucleus.

12. Where does it come from?
How does it happen??
Radiation comes from the
nucleus of the atom.
. . . RADIATION . . . radiation . . .

13. •Everything in the world is composed of
different types of matter (chemical elements).
•Each element consists of very small parts
called the "Atoms".
ATOM
electron
NUCLEUS
ATOM
Typical diameter: ~ 10-10
m
Typical
diameter:
~ 10-15
m

14. NUCLEUS
neutron
proton
particle mass charge location
proton 1 amu + in nucleus
neutron 1 amu no
charge
in nucleus
electron 1/1850
amu
- around nucleus in
various energy
levels
Subatomic Particles
1 amu = 1.675 x 10-27
kg

15. Radioactivity depends on the structure of
the nucleus.
A nucleus should contain “appropriate” # of
neutrons to become stable  non-radioactive
C-12 C-13
C-10 C-11 C-14 C-15
Stable configuration (For Z ≤ 20) :
# of neutrons = or a bit higher than # of protons

16. An unstable nucleus has too much energy in it.
An atom cannot hold this energy forever.
Unstable nuclei make substances
radioactive.
Sooner or later, the atom must
get rid of the excess energy
. . . and return to its normal (stable) state.
radiation

17. WHY, again, do
certain ATOMS DECAY?
Atoms with too much energy in
their nuclei are called "radioactive".
Some nuclear arrangements
are less stable than others.
A radioactive isotope decays
to form a more stable nucleus.

18. … get rid of their
excess energy
(DECAY)
by emitting radiation.
Radioactive isotopes…
They decay by spitting
out:
- mass (alpha particles)
- charge (beta particles)
- energy (gamma rays)

19. PARENT and DAUGHTER
PARENT NUCLIDE – the original nuclide
which undergoes radioactive decay
DAUGHTER NUCLIDE (or progeny)
- the more stable nuclide which results
from radioactive decay

20. NUCLIDE - any atomic species characterized by
the number of protons and number of neutrons
notations: A
zXN X-A A
X
where X: symbol of element
Z: atomic number = no. of protons
N: number of neutrons
A: atomic mass = Z + N
Examples:
60
27Co33 Co-60 60
Co
32
P P-32 32
P

21. ALPHA, 
•A helium nucleus, 4
2He
- Consists of 2 protons and 2 neutrons
•heavy ( Mass : 4 units or 7340 times beta particle )
•Charge : +2
•High energy ( Energy range : 4 to 8 MeV )
•Slow moving ( Speed : 2 X 107
m/s)
•Emitted when the nucleus is too big
•Least penetrating but much damage where it penetrates
- Limited range : < 10 cm in air ; 60 microns in tissue
•Easily Shielded (e.g., paper, skin)

22. (1) alpha decay - emission of an alpha particle (a He
nucleus), resulting in a decrease in both mass and
atomic number.

23. Example: Alpha Decay of Americium-241 to Neptunium-237
α
Np
Am 4
2
237
93
241
95 

- decay
•Heavy nuclei more massive than Pb decay by this method
•Atomic Number, Z, decreases by 2
•Atomic Mass Number, A, decreases by 4
•Products are a new element and an  particle
α
Y
X 4
2
4
A
2
Z
A
Z 
 


24. Beta, 
• A fast moving electron originating from the nucleus
• Emitted when the nucleus has too many neutrons
• Comes from a neutron which has changed into a p+
and an e-
• Very light ( Mass : 0.00055 amu )
• Charge : -1
• Energy dependent on radionuclide
- ( Energy range : several KeV to 5 MeV )
Range : ~ 12' / MeV in air ; few mm in tissue
• Shielding (aluminum and other light (Z<14) materials,
plastics)

25. (2) Beta decay - emission of a beta particle
(an electron from the nucleus), resulting in
an increase in atomic number.

26. - DECAY
•A radioactive nucleus that undergoes - decay has a
neutron in its nucleus convert into a p+
and an e-
•Atomic Number, Z, increases by 1
•Atomic Mass Number, A, remains the same
Example: Beta Decay of Hydrogen-3 to Helium-3.


 
He
H 3
2
3
1

 
 
Y
X A
1
Z
A
Z

28. Gamma, 
•Not a particle but a burst of very high energy as
electromagnetic radiations of very high frequency
•Results from the transition of nuclei from excited state
to their ground state
•No mass, 0 charge
•Have highest energy of all EM radiations
•Very dangerous (can do a lot of biological damage)
•Energies well defined and characteristics of the emitting
radionuclide (up to several MeV)
•Speed : speed of light
• Long range : km in air ; m in body
•Shielding : large amounts of lead or concrete

29. (3) Gamma decay - This is the photon that
carries the energy that is emitted. The
wavelength is in the order of 10-11
to 10-14
m
(higher energy than x-rays).

30.  DECAY
•Only energy is released
•Parent and daughter atoms are the same chem'l element
•Atomic Number, Z, remains the same
•Atomic Mass Number, A, remains the same


 X
X A
Z
A
Z
Example: Gamma Decay of Helium-3.


 He
He 3
2
3
2

32. POSITRON, +
• Similar to e- but opposite charge
• Comes from a proton which has changed
into a neutron and a positron
p+  n + +
• The neutron stays in the nucleus and the
positron ejected at high speed
• Charge : +1

33. POSITRON DECAY
•Occurs in nuclei which have an excess of protons
•Atomic Number, Z, reduces by 1
•Atomic Mass Number, A, remains the same


 
1
A
1
-
Z
A
Z Y
X
•Example: Positron Decay of Carbon-11 to Boron-11.


 
B
C 11
5
11
6
Comes from a proton which has
changed into a neutron and a
positron
p+  n + +

34. ELECTRON CAPTURE
•Occurs in atoms of excess protons
•e- in the innermost shell (K-shell) is captured by a p+
in the nucleus to form a neutron
• always accompanied by emission of x-rays
• x-rays emitted are characteristics of the progeny
nuclide
•Atomic Number, Z, reduces by 1
•Atomic Mass Number, A, remains the same
ray
-
x
Y
X A
1
-
Z
A
Z 

Example: Electron Capture of Beryllium-7.
It decays to Lithium-7.
Li
Be 7
3
7
4


35. (4) positron emission - emission of a positively charged
electron (positron) from the nucleus, resulting in a decrease in
the atomic number. A positron has the same mass as an
electron, but opposite in charge. In other words, inside the
nucleus, a proton is being converted into a neutron.
(5) electron capture - This happens in heavy atoms in which an
inner shell (1s) electron is captured by the nucleus, resulting in a
decrease in atomic number. This process has the same effect as
positron emission.

36. Summary of Radioactive Decay Modes
Decay Mode Symbol Common
Source
Change
in Z
Change
in N
Change
in A
Alpha  Heavy Nuclei - 2 - 2 - 4
Beta -
Excess
Neutrons
+ 1 - 1 0
Gamma  Excited
Nuclei
0 0 0
Positron +
Excess
Protons
- 1 + 1 0
Electron
Capture
 Excess
Protons
- 1 + 1 0

37. Decay Chains / Decay Series
A radionuclide may decay to a
nuclide which is also radioactive.
This radionuclide may in turn give
rise to another radionuclide…
… and this will be repeated until
the atom finally reaches a stable
form.
This path to stability is called a
DECAY CHAIN or a DECAY SERIES.

38. CHART OF NUCLIDES
• a plot of Z vs. N of all known nuclides
• provides several important data
concerning the isotopes
• may be used to determine
how a particular nuclide will decay
• may be used to determine the progeny of a parent nuclide
• decay modes are given in order of abundance
• From the chart it is possible to find nuclides which are stable.
• Stable nuclides form a rough band running diagonally up and to the
right on the chart.
• General Rule : The closer a nuclide is to the line of stability, the
more stable it is.

40. 238 234 230 226 222 218 214 210 206
U-92
Pa-91
Th-90
Ac-89
Ra-88
Fr-87
Rn-86
At-85
Po-84
Bi-83
Pb-82
Tl-81
U
Th Th
Ra
Rn
Po
Pb
Bi
Po
Tl
Pb
Bi
Po
Pb
U
Pa
Atomic Mass Number
Atomic
element
and
number
Uranium-238 Series

41. Alpha
in
Beta-
out
n
out
Original
nucleus
n
in
Beta+
out
Alpha
out
Atomic
Mass
Number
Atomic element and number

42. NUCLEAR EQUATIONS
•Nuclear equations show how atoms decay.
•Similar to chemical equations
- must still balance mass and charge

43. NUCLEAR EQUATIONS
Example:
A patient is injected with radioactive
phosphorus. What happens to the phosphorus?
Is this equation balanced?
You must see if the mass and charge
are the same on both sides.
Charge
+15 (protons) + 16 (protons)
- 1 ()
--------------------------------------
+15 total charge +15 total charge
Yes, it is balanced.
Mass
15 protons 16 protons
17 neutrons 16 neutrons
-------------------------------------
32 total mass 32 total mass
32
15P17  32
16S16 + 

44. DECAY PARAMETERS:
characteristics of specific radionuclide
•ACTIVITY, A
- number of disintegrations of a nucleus occurring per
second
•DECAY CONSTANT, 
- the fractions of atoms which undergo decay per unit
time
•HALF-LIFE, T1/2
- time taken for half the atoms of a radionuclide to
undergo radioactive decay

45. RADIOACTIVE DECAY LAW
N = No e - T
where :
No : original number of nuclei
present
T : time which passed
 : radioactive decay constant
N : remaining nuclei after time T

46. UNITS
ACTIVITY
- described by the number of nuclear
disintegrations per unit time.
1 Becquerel (Bq) = 1 disintegration per second
- named after Henri Becquerel,
discoverer of radioactivity
1 Curie (Ci) = 37 billion disintegrations per second
- named after Marie Curie who discovered and
named radium and polonium
1 Ci = 3.7 x 1010
Bq

47. Activity: how much is present?
Activity – tells how many unstable nuclei decay in
a second and emit radiation
Activity of an object need not be in any proportion
to its size.
High activity Low activity
Radiography
isotope
Low level
waste

48. ACTIVITY, A
Proportional to the number of unstable nuclei
A = N
Can be written in the form:
A = Ao e - T
where:
Ao: original activity of radionuclide
T : time which passed
 : radioactive decay constant
A : remaining activity after decay
time

49. Half-Life

50. Each radioisotope has its own half-life.
Half-life values can range from
milliseconds to billions of years.
Half-life examples:
•Molybdenum-99 67 hours
• Iodine-131 8 days
• Phosphorus-32 14.3 days
• Iron-59 45 days
• Cobalt-60 5.3 years
• Carbon-14 5760 years
• Uranium-235 710 million years

51. HALF-LIFE, T1/2 - time taken for half the atoms of a
radionuclide to undergo radioactive decay
To determine relationship between  and T1/2 :
at T=T1/2 , N = No / 2
substituting to N = No e -T
taking ln of both sides:
2
1
T
e
2
1 


2
1
T
693
.
0


2
1
T
o
o
e
N
2
N 


ln (1/2) = ln e(-T1/2)
- 0.693 = - T

52. CALCULATING ACTIVITY
Activity is also defined as:
Where A : activity at time T
Ao : initial activity
n : number of half-lives which
have elapsed, i.e.
n
o
2
A
A 
2
1
T
T
n 

53. EXAMPLE OF ACTIVITY CALCULATION
PROBLEM:
P-32 has a half-life of 14.3 days. On Jan. 10, 2006, the
activity of the P-32 sample was 10 mCi. What will the
activity be on February 6, 2006?
n
o
2
A
A 
METHOD 1: USE Eqn. 1
SOLUTIONS:
Given:
T = 27 days : Time interval bet Jan. 10, Feb. 6, 2006
T1/2 = 14.3 days : Half-life of P-32
Ao = 10 Ci : Activity of source on Jan. 10, 2006

54. Activity of P-32 on Feb. 6, 2006 is 2.698 mCi.
substituting to Eqn. 1 :
n
o
A
A
2

91
.
1
17
.
30
5
.
57
2
1



y
y
T
T
n
27 days
14.3 days
1.89
mCi
mCi
mCi
A 698
.
2
706
.
3
10
2
10
89
.
1




55. METHOD 2 : USE
T
oe
A
A 

 Eqn. 2
Substituting to Eqn. 2 :
A = 10 e – (0.048 / day) x (27 days)
= 10 e - 1.308
= 10 x 0.27
= 2.7023 Ci
Activity of P-32 on Feb. 6, 2006 is 2.7023 Ci.
Note: Difference is due to rounding adjustments.
1
2
2
1
10
3
.
2
17
.
30
693
.
0
693
.
0 



 y
x
y
T

Where
0.048 / day
14.3 days

56. EXAMPLE OF ACTIVITY CALCULATION
PROBLEM:
A Cs-137 source had an activity of 800 MBq on
Jan. 1, 1973. What will its activity be on July 1, 2030?
n
o
2
A
A 
METHOD 1: USE Eqn. 1
SOLUTIONS:
Given:
T = 57.5 y : Time interval bet Jan. 1, 1973 and July 1, 2030
T1/2 = 30.17 y : Half-life of Cs-137 (from Table of Nuclide)
Ao = 800 MBq : Activity of source on Jan. 1, 1973

57. Computation for T
year , mo. , day
Tf = July 1, 2030  2030 , 7 , 1
Ti = Jan 1, 1973  1973 , 1 , 1
----------------------------------
57 yrs , 6 mo. , 0 days
 57 yrs + 6 mo / 12 mo/yr + 0 days
 57 yrs + 0.5 yrs
-------------------------------------
T = Tf - Ti = 57.5 yrs

58. 91
.
1
17
.
30
5
.
57
2
1



y
y
T
T
n
MBq
MBq
MBq
A 213
76
.
3
800
2
800
91
.
1



Activity of Cs-137 on July 1, 2030 is 213 MBq.
subsituting to Eqn. 1 :
n
o
A
A
2


59. METHOD 2 : USE
T
oe
A
A 

 Eqn. 2
Substituting to Eqn. 2 :
A = 800 e – (0.023 / y) x (57.5 y)
= 800 e - 1.32
= 800 x 0.267
= 214 MBq
Activity of Cs-137 on July 1, 2030 is 214 MBq.
Note: Difference of 1 MBq is due to rounding adjustments.
1
2
2
1
10
3
.
2
17
.
30
693
.
0
693
.
0 



 y
x
y
T

Where
0.023 / y

60. Sample computation for T
Given: Tf = 3:20 pm
Ti = 10:00 am
---------------------------------
5 hrs + 20 mins
Convert hrs to mins:
(5 hrs) X (60 mins/hr) = 300 mins
Add the 20 mins:
300 mins + 20 mins = 320 mins = T
 3 + 12 = 15 hrs , 20 mins
 = 10 hrs, 0 mins

61. Seatwork: Sample computation for T
Given:
Tf = Sept. 12, 1997
Ti = Jan. 1, 1966
---------------------------------
T = Tf – Ti  31 yrs + 8mos. + 11 days
Convert 8 mos. to yrs:
(8 mos.) X (1 yr/12 mos.) = 0.6666 yr
Convert 11 days to yrs:
(11 days) X (1 yr / 365 days) = 0.0301 yr
Add all the numbers converted to yrs:
(31 + 0.6666 + 0.0301) yrs = 31.6967 yrs or 31.70 yrs = T
 1997 , 9 , 12
 1966 , 1 , 1

62. Seatwork:
32
P has a half life of 14.3 days. At 0 day it
has an activity of 1mCi. Compute for the
activity of 32
P after the:
1) 1st
half life :
2) 2nd
half life:
3) 3rd
half life:
4) 4th
half life:

63. EXAMPLE OF HALF-LIFE CALCULATION
PROBLEM : A sample is counted and found to have
952 counts per minute. Seven minutes
later it is measured again and has a count
of 148 counts per minute. A background
measurement gave 6 counts per minute.
What is the half-life of the sample?
SOLUTIONS :
GIVEN:
Initial Activity : Ao
= 952 - 6 = 946 cpm
Activity 7 minutes after : A = 148 - 6 = 142 cpm

64. This means that the number of half-lives (n) in 7
minutes is 2.74.
METHOD 1 : Use n
o
A
A
2

66
.
6
142
946
2 


A
Ao
n
n log 2 = log 6.66
74
.
2
3010
.
0
8235
.
0
2
log
66
.
6
log



n

65. 74
.
2
7
2
1 
T
Using
2
1
T
T
n 
n
T
T 
2
1
Therefore, the half-life of the sample is 2.55 mins.
T1/2 = 2.55 minutes

66. Use
T
o
e
A
A 



T
A
A
ln
o









T
A
A
ln o








T
A
A
ln o








METHOD 2 :
A = Ao e -T

67. 7
142
946
ln 







 
7
66
.
6
ln


7
89
.
1


271
.
0


Then use:
2
1
693
.
0
T



693
.
0
2
1 
 T
271
.
0
693
.
0
2
1 
T
T1/2 = 2.55 minutes

68. THANK YOU for your attention.