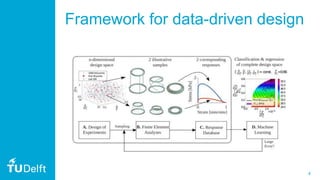
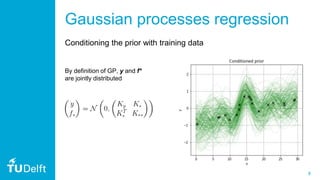
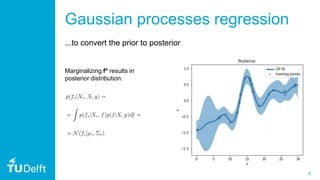
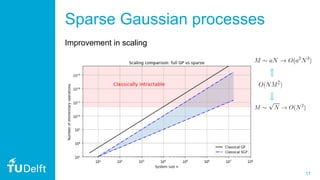
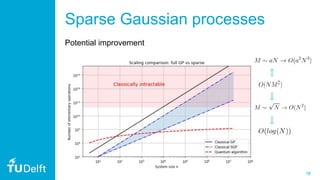
1. The document discusses quantum Gaussian processes (QGP), which use quantum computing to speed up Gaussian process regression by efficiently inverting matrices using the HHL algorithm. 2. It presents the concept of using QGP to find the inverse of a matrix A multiplied by a vector v, which can then be used to calculate the dot product of another vector u with the result. This provides an exponential speedup over classical computation. 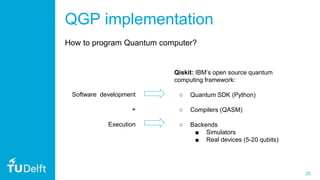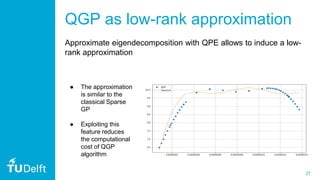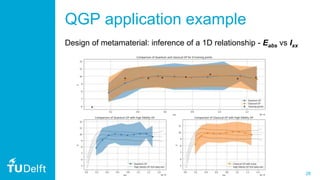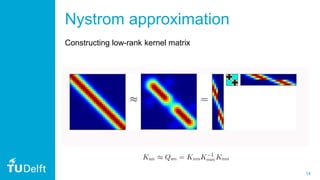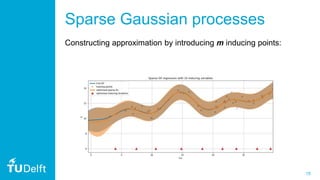3. The document also discusses practical considerations in implementing QGP, such as using the Qiskit framework, and how approximations in quantum phase estimation can induce a low-rank approximation similar to sparse Gaussian processes classically. It provides an example application to model a relationship in metamaterial

1. 1
Quantum Gaussian
Processes
Gaweł Kuś
Master student at Novel Aerospace Materials (NovAM) group,
Faculty of Aerospace Engineering
Delft University of Technology
Dr.ir. M.A. (Miguel) Bessa
Assistant Professor in Materials Science and Engineering
Delft University of Technology
Prof.Dr.ir. S. (Sybrand) van der Zwaag
Chairholder of Novel Aerospace Materials (NovAM) group,
Faculty of Aerospace Engineering
Delft University of Technology
for computational design of materials

2. 2
Example material design problem
Unit cell of super-compressible metamaterial
Objective:
• Optimize for absorbed energy: Eabs
• Optimize for buckling load: Pcrit

3. 3
Parameter Description
1. D1 /D2 Ratio of diameters
2. P Pitch
3. Ixx Moment of inertia of longeron around x
4. Ixx Moment of inertia of longeron around y
5. J Torsional stiffness of longeron
6. A Cross-section of longeron
7 G/E Shear modulus/Young’s modulus
Objective:
• Optimize for absorbed energy: Eabs
• Optimize for buckling load: Pcrit
Example material design problem
Unit cell of super-compressible metamaterial

4. 4
Framework for data-driven design

5. 5
Gaussian processes regression
● Inference from noisy data
● Uncertainty quantification
● Bayesian Machine learning
GP applications:
● Optimization under uncertainty
● Modelling of imperfection
sensitive phenomena

6. 6
Gaussian processes regression
GP assumes a prior distribution
Fully specified by:
● Mean:
● Covariance matrix: K
given by kernel
function, e.g. RBF

7. 7
Kernel function
Radial basis function (RBF) as a measure of similarity

8. 8
Gaussian processes regression
Conditioning the prior with training data
By definition of GP, y and f*
are jointly distributed

9. 9
Gaussian processes regression
...to convert the prior to posterior
Marginalizing f* results in
posterior distribution:

10. 10
● Matrix inversion scales as:
● Practical limitation: ~10 000
training points
Gaussian processes regression
In practice: solving system of linear equations

11. 11
The curse of dimensionality
In design of materials
High-dimensional design spaces, due to
phenomena at many different levels:
● Nanoscale:
-chemical composition
-crystalline structure, phases
-imperfections
● Microscale:
-microstructural
parameters
● Macroscale
-macro-architecture
parameters
Big data

12. 12
Idea 1: PCA approximation
Eigendecomposition of Knn and select m<n eigenmodes:
But, eigendecomposition ~O(n3)
Overcoming the limitations of GP
How to improve scalability?

13. 13
Idea 1: PCA approximation
Eigendecomposition of Knn and select m<n eigenmodes:
But, eigendecomposition ~O(n3)
Idea 2: Nystrom approximation
Approximate m eigenfunctions to construct a low-rank approximation:
Inversion complexity:
Overcoming the limitations of GP
How to improve scalability?

14. 14
Nystrom approximation
Constructing low-rank kernel matrix

15. 15
Sparse Gaussian processes
Constructing approximation by introducing m inducing points:

16. 16
Sparse Gaussian processes
Number of inducing points (m) affects the approximation quality

17. 17
Sparse Gaussian processes
Improvement in scaling

18. 18
Sparse Gaussian processes
Potential improvement

19. 19
Quantum computing and machine learning use similar formulation
(linear algebra)
Common trend in QML: replacing BLAS with qBLAS
Quantum algorithm Function Application in ML
QPE eigendecomposition - qPCA
HHL Solving systems of
linear equations
- SVM
- Least squares
- Kernel methods
- Gaussian
Processes
Quantum machine learning

20. 20
u vA
[1] Z.Zhao et al., Quantum assisted Gaussian process regression (2015)
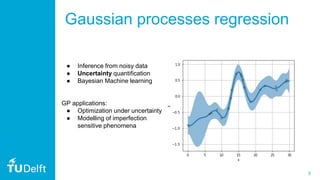
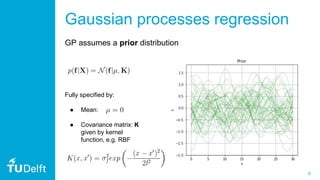
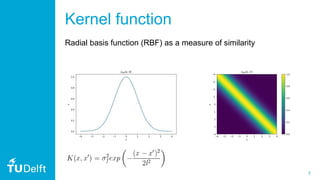
Quantum Gaussian processes
Concept: speed-up the matrix inversion with HHL algorithm[1]

21. 21
u vA
1. Find b = A-1v with HHL algorithmb = A-1v
[1] Z.Zhao et al., Quantum assisted Gaussian process regression (2015)
Quantum Gaussian processes
Concept: speed-up the matrix inversion with HHL algorithm[1]

22. 22
u vA
1. Find b = A-1v with HHL algorithm
2. Apply a measurement operator to
find the dot product: u.b = uA-1v
b = A-1v
u.b = u.A-1.v
u
[1] Z.Zhao et al., Quantum assisted Gaussian process regression (2015)
Quantum Gaussian processes
Concept: speed-up the matrix inversion with HHL algorithm[1]

23. 23
Quantum Gaussian processes
Concept: speed-up the matrix inversion with HHL algorithm[1]
u vA
1. Find b = A-1v with HHL algorithm
2. Apply a measurement operator to
find the dot product: u.b = uA-1v
Exponential speed-up due to HHL:
[1] Z.Zhao et al., Quantum assisted Gaussian process regression (2015)

24. 24
find b = A-1v dot product:
u.b = uA-
1v
Initialize u and v
in superposition
Quantum Gaussian processes
Circuit representation

25. 25
QGP implementation
How to program Quantum computer?
Qiskit: IBM’s open source quantum
computing framework:
○ Quantum SDK (Python)
○ Compilers (QASM)
○ Backends
■ Simulators
■ Real devices (5-20 qubits)
Software development
+
Execution

26. 26
Approximations in QGP
Eigendecomposition approximation with QPE
QPE is controlled with 2 parameters:
● r - number of time slices
-controls the matrix
exponentiation
● k - size of the eigenvalue register
- controls the eigenspectrum
discretization
- min. resolvable eigenvalue:

27. 27
QGP as low-rank approximation
Approximate eigendecomposition with QPE allows to induce a low-
rank approximation
● The approximation
is similar to the
classical Sparse
GP
● Exploiting this
feature reduces
the computational
cost of QGP
algorithm

28. 28
QGP application example
Design of metamaterial: inference of a 1D relationship - Eabs vs Ixx

29. 29
Conclusions
● Discovered a mechanism for inducing the low-rank approximation, analog to
that in classical sparse Gaussian processes
● Demonstrated application of QC in materials engineering