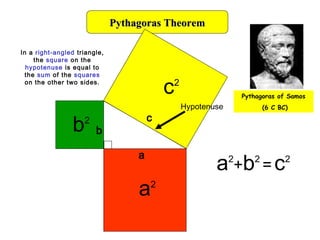
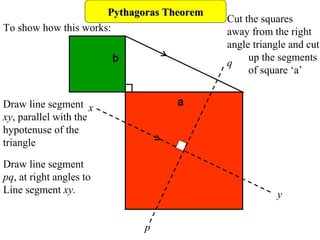
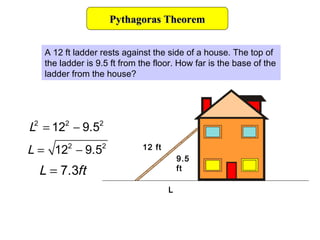
1) The Pythagorean theorem states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. 2) The document provides examples of applying the Pythagorean theorem to solve for missing sides of right triangles. 3) Pythagoras' theorem can be used to calculate distances in real world problems, like finding the total distance traveled by a boat or calculating how far a ladder's base is from a house.

1. Pythagoras TheoremPythagoras Theorem
Reminder of square numbers:
12
= 1 x 1 = 1
22
= 2 x 2 = 4
32
= 3 x 3 = 9
42
= 4 x 4 = 16
32
Base number
Index number
The index number tells us how
many times the base number
is multiplied by itself.
e.g. 34
means 3 x 3 x 3 x 3 = 81
1,4,9,16, …. are the answers to a number being squared so they
are called square numbers.

2. Pythagoras TheoremPythagoras Theorem
Square root means think what is multiplied by itself to
make this number?
Answer these questions:
=1
=4
=9
=16
=49
=81
=211
=001
1
2
3
4
7
9
11
10
Use your calculator to answer
these questions:
=8.5
=4.25
=169
=400
=1000
=8100
=225
=361
2.408
5.040
13
20
31.623
90
15
19

3. Pythagoras TheoremPythagoras Theorem
c2
b2
a2
a2
+b2
= c2
b
a
c
In a right-angled triangle,
the square on the
hypotenuse is equal to
the sum of the squares
on the other two sides.
Hypotenuse
Pythagoras of Samos
(6 C BC)

4. b
a
Cut the squares
away from the right
angle triangle and cut
up the segments
of square ‘a’
Draw line segment
xy, parallel with the
hypotenuse of the
triangle
x
y
q
p
Draw line segment
pq, at right angles to
Line segment xy.
Pythagoras TheoremPythagoras Theorem
To show how this works:

5. Now rearrange them
to look like this.
You can see that they
make a square with
length of side ‘c’.
This demonstrates that
the areas of squares
a and b
add up to be the
area of square c
a2
+b2
= c2

6. 2 2 2
3 4x = +
2 2
3 4x = +
5 cmx =
2 2 2
5 12x = +
2 2
5 12x = +
13 cmx =
3 cm
4 cm
x
1
5 cm
12 cm
x
2
Pythagoras TheoremPythagoras Theorem
9 + 16x =
25x =
169x =

7. Pythagoras TheoremPythagoras Theorem
2 2 2
5 6x = +
2 2
5 6x = +
7.8 cm (1 dp)x =
2 2 2
4.6 9.8x = +
2 2
4.6 9.8x = +
10.8 cm (1 dp)x =
5 cm
6 cm
x
3
4.6
cm
9.8 cm
x
4

8. Pythagoras TheoremPythagoras Theorem
Now do these:
x m
9 m
11m5
11 cm
23.8 cm6
x m
7.1 cm
x cm
3.4 cm7
8
25 m
7 m
x m
2 2 2
11 9x = −
2 2
11 9x = −
6.3 m (1 dp)x =
2 2 2
23.8 11x = −
2 2
23.8 11x = −
21.1 cm (1 dp)x =
2 2 2
7.1 3.4x = +
2 2
7.1 3.4x = +
7.9 cm (1 dp)x =
2 2 2
25 7x = −
2 2
25 7x = −
24 mx =

9. Pythagoras TheoremPythagoras Theorem
A boat sails due East from a Harbour (H), to a marker buoy (B),15 miles away.
At B the boat turns due South and sails for 6.4 miles to a Lighthouse (L). It then
returns to harbour. What is the total distance travelled by the boat?
2 2 2
15 6.4LH = +
2 2
15 6.4LH = +
16.3 milesLH =
∴Total distance travelled = 21.4 + 16.4 = 37.7 miles
H
B
L
15 miles
6.4
miles

10. Pythagoras TheoremPythagoras Theorem
12 ft
9.5
ft
L
A 12 ft ladder rests against the side of a house. The top of
the ladder is 9.5 ft from the floor. How far is the base of the
ladder from the house?
2 2 2
12 9.5L = −
2 2
12 9.5L = −
7.3L ft=