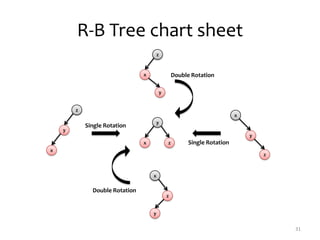
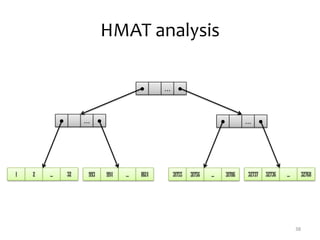
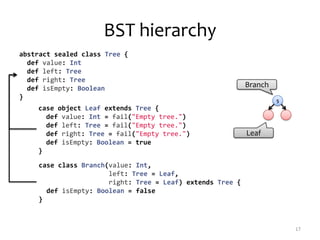
The document discusses purely functional data structures in Scala, focusing on immutability, persistence, and various data structures such as singly-linked lists, banker’s queues, binary search trees, and red-black trees. It explores the performance characteristics and implementation details of these structures, highlighting concepts like structural sharing and amortized analysis. Additionally, it mentions Scala's built-in support for these data structures and provides references for further reading.

1. Purely Functional
Data Structures in Scala
Vladimir Kostyukov
http://vkostyukov.ru

2. Agenda
• Immutability & Persistence
• Singly-Linked List
• Banker’s Queue
• Binary Search Tree
• Balanced BST: Red-Black Tree
• Scala support of these things
• Patricia Trie
• Hash Array Mapped Trie
2

3. Immutability & Persistence
Two problems:
• FP paradigm doesn’t support destructive updates
• FP paradigm expects both the old and new
versions of DS will be available after update
Two solutions:
• Immutable objects aren’t changeable
• Persistent objects support multiple versions
3

4. Singly-Linked List
4
35 7
Cons
Nil
abstract sealed class List {
def head: Int
def tail: List
def isEmpty: Boolean
}
case object Nil extends List {
def head: Int = fail("Empty list.")
def tail: List = fail("Empty list.")
def isEmpty: Boolean = true
}
case class Cons(head: Int, tail: List = Nil) extends List {
def isEmpty: Boolean = false
}

5. List: analysis
5
35 7A =
B = Cons(9, A) = 9
C = Cons(1, Cons(8, B)) = 1 8
structural sharing

6. /**
* Time - O(1)
* Space - O(1)
*/
def prepend(x: Int): List = Cons(x, this)
/**
* Time - O(n)
* Space - O(n)
*/
def append(x: Int): List =
if (isEmpty) Cons(x)
else Cons(head, tail.append(x))
List: append & prepend
6
35 79
35 7 9

7. List: apply
7
35 7 42 6
n - 1
/**
* Time - O(n)
* Space - O(n)
*/
def apply(n: Int): A =
if (isEmpty) fail("Index out of bounds.")
else if (n == 0) head
else tail(n - 1) // or tail.apply(n - 1)

8. List: concat
8
path copying
A = 42 6
B = 35 7
C = A.concat(B) = 42 6
/**
* Time - O(n)
* Space - O(n)
*/
def concat(xs: List): List =
if (isEmpty) xs
else tail.concat(xs).prepend(head)

9. List: reverse (two approaches)
9
42 6 46 2reverse( ) =
def reverse: List =
if (isEmpty) Nil
else tail.reverse.append(head)
, or tail recursion in O(n)
The straightforward solution in O(n2)
def reverse: List = {
@tailrec
def loop(s: List, d: List): List =
if (s.isEmpty) d
else loop(s.tail, d.prepend(s.head))
loop(this, Nil)
}

10. List performance
10
prepend
head
tail
append
apply
reverse
concat

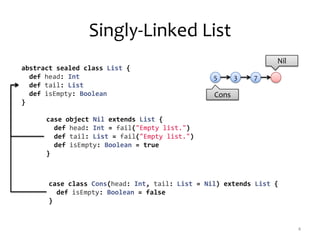
11. Banker’s Queue
• Based on two lists (in and out)
• Guarantees amortized O(1) performance
11
class Queue(in: List[Int] = Nil, out: List[Int] = Nil) {
def enqueue(x: Int): Queue = ???
def dequeue: (Int, Queue) = ???
def front: Int = dequeue match { case (a, _) => a }
def rear: Queue = dequeue match { case (_, q) => q }
def isEmpty: Boolean = in.isEmpty && out.isEmpty
}

12. Queue: analysis
12
A = new Queue( , )
B = A.enqueue(1) = 1 , )
C = B.enqueue(2) = 12 , )
D = C.enqueue(3) = 23 1 , )
(V, E) = D.dequeue = , ))2 3
(U, F) = E.dequeue = , ))3
reverse
new Queue(
new Queue(
new Queue(
(1, new Queue(
(2, new Queue(

13. Amortized vs. Average Case
• Average Case analysis makes assumptions about
typical (most likely) input
• Amortized analysis considers total performance of
sequence of operations in a the worst case
Example:
• Dynamically-Resizing Array (java.util.ArrayList)
– Has O(n) average case performance for add operation
– It can be amortized to O(1)
• Usually it takes O(1) since the storage is big enough
• Sometimes it can take O(n) due to reallocation & copying
13

14. Queue: enqueue & dequeue
14
/**
* Time - O(1)
* Space - O(1)
*/
def enqueue(x: Int): Queue = new Queue(x :: in, out)
/**
* Time - O(1)
* Space - O(1)
*/
def dequeue: (Int, Queue) = out match {
case hd :: tl => (hd, new Queue(in, tl)) // O(1)
case Nil => in.reverse match { // O(n)
case hd :: tl => (hd, new Queue(Nil, tl))
case Nil => fail("Empty queue.")
}
}

15. Queue performance
15
enqueue
dequeue*
front*
rear*
* amortized complexity

16. Binary Search Tree
16
5
2 7
1 3 8

17. BST hierarchy
17
abstract sealed class Tree {
def value: Int
def left: Tree
def right: Tree
def isEmpty: Boolean
}
case object Leaf extends Tree {
def value: Int = fail("Empty tree.")
def left: Tree = fail("Empty tree.")
def right: Tree = fail("Empty tree.")
def isEmpty: Boolean = true
}
case class Branch(value: Int,
left: Tree = Leaf,
right: Tree = Leaf) extends Tree {
def isEmpty: Boolean = false
}
5
Branch
Leaf

18. BST: analysis
18
A = Branch(5) = 5
B = Branch(7, A, Branch(9)) = 7
9
C = Branch(1, Leaf, B) = 1
structural sharing

19. BST: insert
19
5
2 7
1 3 86
path copying
7
5
/**
* Time - O(log n)
* Space - O(log n)
*/
def add(x: Int): Tree =
if (isEmpty) Branch(x)
else if (x < value) Branch(value, left.add(x), right)
else if (x > value) Branch(value, left, right.add(x))
else this

20. BST: remove (cases)
20
5
2 7
1 3 8
5
2 7
1 3 8
5
2 7
1 3 8

21. BST: remove (code)
21
/**
* Time - O(log n)
* Space - O(log n)
*/
def remove(x: Int): Tree =
if (isEmpty) fail("Can't find " + x + " in this tree.")
else if (x < value) Branch(value, left.remove(x), right)
else if (x > value) Branch(value, left, right.remove(x))
else {
if (left.isEmpty && right.isEmpty) Leaf // case 1
else if (left.isEmpty) right // case 2
else if (right.isEmpty) left // case 2
else { // case 3
val succ = right.min // case 3
Branch(succ, left, right.remove(succ)) // case 3
}
}

22. /**
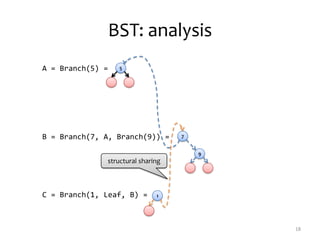
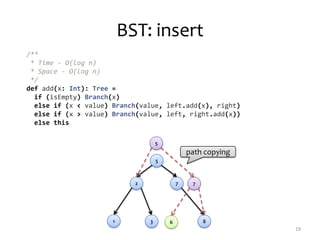
* Time - O(log n)
* Space - O(log n)
*/
def min: Int = {
@tailrec def loop(t: Tree, m: Int): Int =
if (t.isEmpty) m else loop(t.left, t.value)
if (isEmpty) fail("Empty tree.")
else loop(left, value)
}
/**
* Time - O(log n)
* Space - O(log n)
*/
def max: Int = {
@tailrec def loop(t: Tree[Int], m: Int): Int =
if (t.isEmpty) m else loop(t.right, t.value)
if (isEmpty) fail("Empty tree.")
else loop(right, value)
}
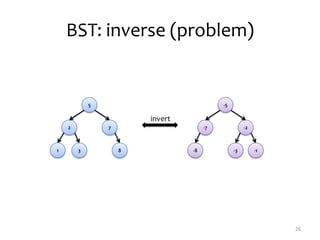
BST: min & max
22
5
2 7
1 3 8
5
2 7
1 3 8

23. BST: apply
23
5
2 7
1 3 6 8
n - 1
/**
* Time - O(log n)
* Space - O(log n)
*/
def apply(n: Int): A =
if (isEmpty) fail("Tree doesn't contain a " + n + "th element.")
else if (n < left.size) left(n)
else if (n > left.size) right(n - size - 1)
else value

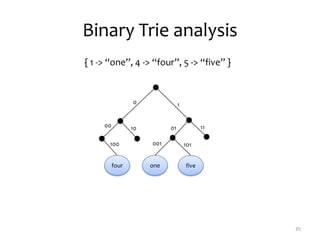
24. BST: DFS (pre-order traversal)
24
/**
* Time - O(n)
* Space - O(log n)
*/
def valuesByDepth: List[Int] = {
def loop(s: List[Tree]): List[Int] =
if (s.isEmpty) Nil
else if (s.head.isEmpty) loop(s.tail)
else s.head.value :: loop(s.head.right :: s.head.left :: s.tail)
loop(List(this))
}
5
2 7
1 3 8

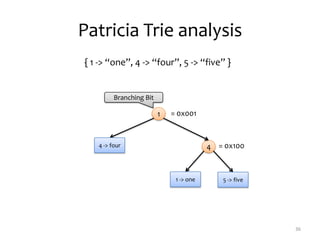
25. BST: BFS (level-order traversal)
25
/**
* Time - O(n)
* Space - O(log n)
*/
def valuesByBreadth: List[Int] = {
import scala.collection.immutable.Queue
def loop(q: Queue[Tree]): List[Int] =
if (q.isEmpty) Nil
else if (q.head.isEmpty) loop(q.tail)
else q.head.value :: loop(q.tail :+ q.head.left :+ q.head.right)
loop(Queue(this))
}
5
2 7
1 3 8

26. BST: inverse (problem)
26
-5
-7 -2
-8 -3 -1
5
2 7
1 3 8
invert

27. BST: inverse (solution)
27
/**
* Time - O(n)
* Space - O(log n)
*/
def invert: Tree =
if (isEmpty) Leaf else Branch(-value, right.invert, left.invert)

28. BST performance
28
insert
contains
remove
min
max
apply
bfs
dfs

29. How fast BST?
29
It’s extremely fast if it’s balanced

30. Balanced BST: Red-Black Tree
• Red invariant: No red node has red parent
• Black invariant: Every root-to-leaf path contains
the same number of black nodes
• Suggested by Chris Okasaki in his paper “Red-Black
Trees in a Functional Settings”
• Asymptotically optimal implementation
• Easy to understand and implement
30

31. R-B Tree chart sheet
31
z
y
x
x
y
z
z
y
x
z
x
y
x
z
y
Double Rotation
Double Rotation
Single Rotation
Single Rotation

32. R-B Tree: balanced insert
32
def balancedAdd(x: Int): Tree =
if (isEmpty) RedBranch(x)
else if (x < value) balance(isBlack, value, left.balancedAdd(x), right)
else if (x > value) balance(isBlack, value, left, right.balancedAdd(x))
else this
def balance(b: Boolean, x: Int, left: Tree, right: Tree): Tree =
(b, left, right) match {
case (true, RedBranch(y, RedBranch(z, a, b), c), d) =>
BlackBranch(y, RedBranch(z, a, b), RedBranch(x, c, d))
case (true, a, RedBranch(y, b, RedBranch(z, c, d))) =>
BlackBranch(y, RedBranch(x, a, b), RedBranch(z, c, d))
case (true, RedBranch(z, a, RedBranch(y, b, c)), d) =>
BlackBranch(y, RedBranch(z, a, b), RedBranch(x, c, d))
case (true, a, RedBranch(z, RedBranch(y, b, c), d)) =>
BlackBranch(y, RedBranch(x, a, b), RedBranch(z, c, d))
case (true, _, _) => BlackBranch(x, left, right)
case (false, _, _) => RedBranch(x, left, right)
}

33. What about Scala?
• Scala has Singly-Linked List
– scala.collection.immutable.List
• Scala has Banker’s Queue
– scala.collection.immutable.Queue
• Scala has Balanced BST (R-B Tree)
– scala.collection.immutable.TreeSet
– scala.collection.immutable.TreeMap
• And a bit more …
33

34. Patricia Trie
34

35. Binary Trie analysis
35
{ 1 -> “one”, 4 -> “four”, 5 -> “five” }
0 1
00 10 1101
100
four
001 101
one five

36. Patricia Trie analysis
36
{ 1 -> “one”, 4 -> “four”, 5 -> “five” }
1
44 -> four
1 -> one 5 -> five
Branching Bit
= 0x001
= 0x100

37. Hash Array Mapped Trie
37

38. HMAT analysis
38
● ... ●
● ... ● ● ... ●
1 2 ... 32 993 994 ... 1024 31755 31756 ... 31786 32737 32736 ... 32768

39. Bedtime Reading
• Okasaki’s Purely Functional Data Structures
• http://okasaki.blogspot.com/
• https://github.com/vkostyukov/scalacaster
• http://www.codecommit.com/blog/
• http://cstheory.stackexchange.com/questions/1539/whats-new-in-
purely-functional-data-structures-since-okasaki
39

40. 40
vkostyukov
vkostyukov