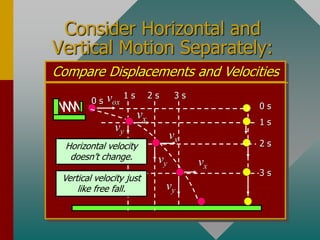
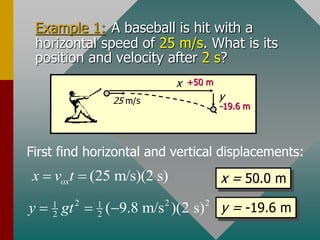
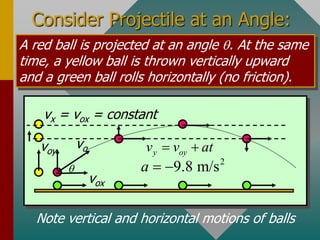
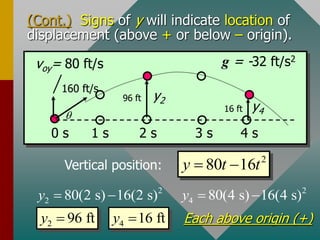
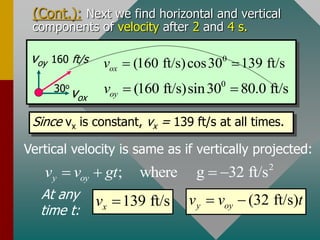
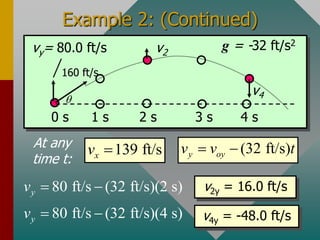
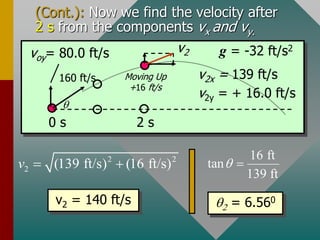
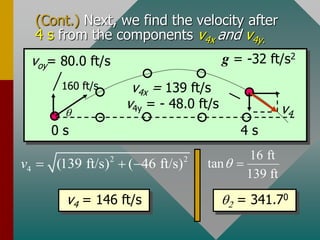
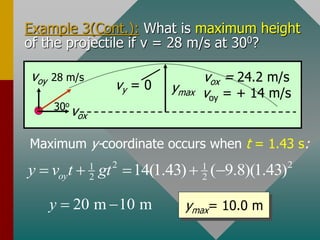
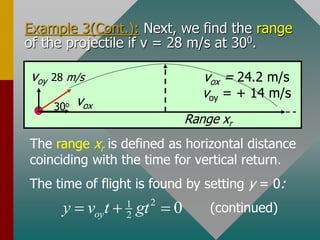
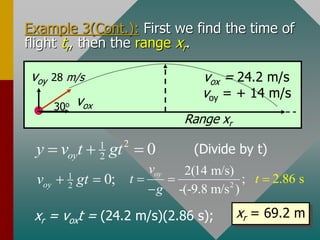
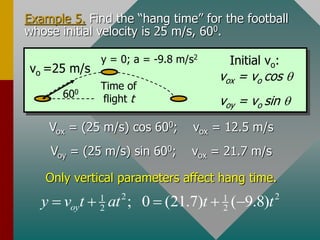
The document describes projectile motion and provides examples to solve problems involving the horizontal and vertical motion of projectiles. It begins by explaining that projectile motion can be treated by separating the horizontal and vertical components of position and velocity. Examples are then provided to demonstrate solving for position, velocity, time, maximum height, and range given initial velocity and launch angle. Key equations for displacement, velocity, and problem-solving strategies are also outlined.

1. Chapter 2 – Projectile Motion

2. Objectives: After completing this
module, you should be able to:
 Describe the motion of a projectile by
treating horizontal and vertical components
of its position and velocity.
• Solve for position, velocity, or time when
given initial velocity and launch angle.

3. Projectile Motion
A projectile is a particle moving near the
Earth’s surface under the influence of its
weight only (directed downward).
a = g
W
W
W

4. Vertical and Horizontal Motion
Simultaneously dropping
yellow ball and projecting
red ball horizontally.
Click right to observe
motion of each ball.

5. Vertical and Horizontal Motion
Simultaneously dropping a
yellow ball and projecting a
red ball horizontally.
Why do they strike the
ground at the same time?
Once motion has begun, the downward
weight is the only force on each ball.
W W

6. Ball Projected Horizontally and
Another Dropped at Same Time:
0 s
vox
Vertical Motion is the Same for Each Ball
1 s
2 s
3 s
vy
vx
vx
vx
vy
vy
vy
vy
vy

7. Observe Motion of Each Ball
0 s
vox
Vertical Motion is the Same for Each Ball
3 s
2 s
1 s

8. Consider Horizontal and
Vertical Motion Separately:
Compare Displacements and Velocities
0 s
0 s
1 s
vox
2 s 3 s
1 s
vy
2 s
vx
vy
3 s
vx
vy
Horizontal velocity
doesn’t change.
Vertical velocity just
like free fall.
vx

9. Displacement Calculations for
Horizontal Projection:
For any constant acceleration:
Horizontal displacement: ox
x v t

Vertical displacement:
2
1
2
y gt

2
1
2
o
x v t at
 
For the special case of horizontal projection:
0; 0;
x y oy ox o
a a g v v v
   

10. Velocity Calculations for Horizontal
Projection (cont.):
For any constant acceleration:
Horizontal velocity: x ox
v v

Vertical velocity: y o
v v gt
 
f o
v v at
 
For the special case of a projectile:
0; 0;
x y oy ox o
a a g v v v
   

11. Example 1: A baseball is hit with a
horizontal speed of 25 m/s. What is its
position and velocity after 2 s?
First find horizontal and vertical displacements:
(25 m/s)(2 s)
ox
x v t
 
2 2 2
1 1
2 2 ( 9.8 m/s )(2 s)
y gt
  
x = 50.0 m
y = -19.6 m
25 m/s
x
y
-19.6 m
+50 m

12. Example 1 Cont.): What are the velocity
components after 2 s?
25 m/s
Find horizontal and vertical velocity after 2 s:
(25 m/s)
x ox
v v
 
2
0 ( 9.8 m/s )(2 s)
y oy
v v at
    
vx = 25.0 m/s
vy = -19.6 m/s
vx
vy
v0x = 25 m/s
v0y = 0

13. Consider Projectile at an Angle:
A red ball is projected at an angle q. At the same
time, a yellow ball is thrown vertically upward
and a green ball rolls horizontally (no friction).
Note vertical and horizontal motions of balls
q
voy
vox
vo
vx = vox = constant
y oy
v v at
 
2
9.8 m/s
a  

14. Displacement Calculations For
General Projection:
The components of displacement at time t are:
2
1
2
ox x
x v t a t
 
For projectiles: 0; ; 0;
x y oy ox o
a a g v v v
   
2
1
2
oy y
y v t a t
 
Thus, the displacement
components x and y for
projectiles are:
2
1
2
ox
oy
x v t
y v t gt

 

15. Velocity Calculations For
General Projection:
The components of velocity at time t are:
x ox x
v v a t
 
For projectiles: 0; ; 0;
x y oy ox o
a a g v v v
   
y oy y
v v a t
 
Thus, the velocity
components vx and vy
for projectiles are:
constant
x ox
y oy
v v
v v gt

 

16. Problem-Solving Strategy:
1. Resolve initial velocity vo into components:
vo
vox
voy
q cos ; sin
ox o oy o
v v v v
q q
 
2. Find components of final position and velocity:
2
1
2
ox
oy
x v t
y v t gt

 
Displacement: Velocity:
0
2
x x
y oy
v v
v v gt

 

17. Problem Strategy (Cont.):
3. The final position and velocity can be found
from the components.
R
x
y
q
4. Use correct signs - remember g is negative or
positive depending on your initial choice.
2 2
; tan
y
R x y
x
q
  
2 2
; tan
y
x y
x
v
v v v
v
q
  
vo
vox
voy
q

18. Example 2: A ball has an initial velocity of
160 ft/s at an angle of 30o with horizontal.
Find its position and velocity after 2 s and
after 4 s.
voy 160 ft/s
vox
30o
Since vx is constant, the horizontal displacements
after 2 and 4 seconds are:
(139 ft/s)(2 s)
ox
x v t
  x = 277 ft
(139 ft/s)(4 s)
ox
x v t
  x = 554 ft
0
(160 ft/s)cos30 139 ft/s
ox
v  
0
(160 ft/s)sin30 80.0 ft/s
oy
v  

19. Note: We know ONLY the horizontal location
after 2 and 4 s. We don’t know whether it is on
its way up or on its way down.
x2 = 277 ft x4 = 554 ft
Example 2: (Continued)
voy 160 ft/s
vox
30o
277 ft 554 ft
2 s 4 s

20. Example 2 (Cont.): Next we find the vertical
components of position after 2 s and after 4 s.
voy= 80 ft/s
160 ft/s
q
0 s 3 s
2 s
1 s 4 s
g = -32 ft/s2
y2
y4
2 2 2
1 1
2 2
(80 ft/s) ( 32 ft/s )
oy
y v t gt t t
    
The vertical displacement as function of time:
2
80 16
y t t
  Observe consistent units.

21. (Cont.) Signs of y will indicate location of
displacement (above + or below – origin).
voy= 80 ft/s
160 ft/s
q
0 s 3 s
2 s
1 s 4 s
g = -32 ft/s2
y2
y4
Vertical position:
2
80 16
y t t
 
2
2 80(2 s) 16(2 s)
y   2
4 80(4 s) 16(4 s)
y  
2 96 ft
y  4 16 ft
y 
96 ft
16 ft
Each above origin (+)

22. (Cont.): Next we find horizontal and vertical
components of velocity after 2 and 4 s.
Since vx is constant, vx = 139 ft/s at all times.
Vertical velocity is same as if vertically projected:
2
; where g 32 ft/s
y oy
v v gt
   
At any
time t:
(32 ft/s)
y oy
v v t
 
139 ft/s
x
v 
voy 160 ft/s
vox
30o
0
(160 ft/s)cos30 139 ft/s
ox
v  
0
(160 ft/s)sin30 80.0 ft/s
oy
v  

23. v2y = 16.0 ft/s
v4y = -48.0 ft/s
Example 2: (Continued)
vy= 80.0 ft/s
160 ft/s
q
0 s 3 s
2 s
1 s 4 s
g = -32 ft/s2
v2
v4
At any
time t:
(32 ft/s)
y oy
v v t
 
139 ft/s
x
v 
80 ft/s (32 ft/s)(2 s)
y
v  
80 ft/s (32 ft/s)(4 s)
y
v  

24. At 2 s: v2x = 139 ft/s; v2y = + 16.0 ft/s
Example 2: (Continued)
vy= 80.0 ft/s
160 ft/s
q
0 s 3 s
2 s
1 s 4 s
g = -32 ft/s2
v2
v4
Moving Up
+16 ft/s
Moving down
-48 ft/s
The signs of vy indicate whether motion is
up (+) or down (-) at any time t.
At 4 s: v4x = 139 ft/s; v4y = - 48.0 ft/s

25. (Cont.): The displacement R2,q is found from
the x2 and y2 component displacements.
q
0 s 2 s 4 s
y2 = 96 ft
x2= 277 ft
R2
2 2
R x y
  tan
y
x
q 
2 2
(277 ft) (96 ft)
R  
96 ft
tan
277 ft
q 
R2 = 293 ft q2 = 19.10
t = 2 s

26. (Cont.): Similarly, displacement R4,q is found
from the x4 and y4 component displacements.
2 2
(554 ft) (64 ft)
R  
64 ft
tan
554 ft
q 
R4 = 558 ft q4 = 6.590
q
0 s 4 s
y4 = 64 ft
x4= 554 ft
R4
2 2
R x y
  tan
y
x
q 
t = 4 s

27. (Cont.): Now we find the velocity after
2 s from the components vx and vy.
2 2
2 (139 ft/s) (16 ft/s)
v  
16 ft
tan
139 ft
q 
v2 = 140 ft/s q2 = 6.560
voy= 80.0 ft/s
160 ft/s
q
0 s 2 s
g = -32 ft/s2
v2
Moving Up
+16 ft/s
v2x = 139 ft/s
v2y = + 16.0 ft/s

28. (Cont.) Next, we find the velocity after
4 s from the components v4x and v4y.
2 2
4 (139 ft/s) ( 46 ft/s)
v   
16 ft
tan
139 ft
q 
v4 = 146 ft/s q2 = 341.70
voy= 80.0 ft/s
160 ft/s
q
0 s 4 s
g = -32 ft/s2
v4
v4x = 139 ft/s
v4y = - 48.0 ft/s

29. Example 3: What are maximum height and
range of a projectile if vo = 28 m/s at 300?
ymax occurs when 14 – 9.8t = 0 or t = 1.43 s
Maximum y-coordinate occurs when vy = 0:
voy 28 m/s
vox
30o
ymax
vy = 0
2
14 m/s ( 9.8 m/s ) 0
y oy
v v gt t
     
vox = 24.2 m/s
voy = + 14 m/s
0
(28 m/s)cos30 24.2 m/s
ox
v  
0
(28 m/s)sin30 14 m/s
oy
v  

30. Example 3(Cont.): What is maximum height
of the projectile if v = 28 m/s at 300?
Maximum y-coordinate occurs when t = 1.43 s:
ymax= 10.0 m
voy 28 m/s
vox
30o
ymax
vy = 0
vox = 24.2 m/s
voy = + 14 m/s
2 2
1 1
2 2
14(1.43) ( 9.8)(1.43)
oy
y v t gt
    
20 m 10 m
y  

31. Example 3(Cont.): Next, we find the range
of the projectile if v = 28 m/s at 300.
The range xr is defined as horizontal distance
coinciding with the time for vertical return.
voy 28 m/s
vox
30o
vox = 24.2 m/s
voy = + 14 m/s
Range xr
The time of flight is found by setting y = 0:
2
1
2 0
oy
y v t gt
   (continued)

32. Example 3(Cont.): First we find the time of
flight tr, then the range xr.
voy 28 m/s
vox
30o
vox = 24.2 m/s
voy = + 14 m/s
Range xr
1
2 0;
oy
v gt
 
(Divide by t)
2
1
2 0
oy
y v t gt
  
xr = voxt = (24.2 m/s)(2.86 s); xr = 69.2 m
2
2(14 m/s)
;
-(-9.8 m/
2.86
s )
s
oy
t
v
t
g

 


33. Example 4: A ball rolls off the top of a
table 1.2 m high and lands on the floor
at a horizontal distance of 2 m. What
was the velocity as it left the table?
1.2 m
2 m
First find t from y equation:
0
½(-9.8)t2 = -(1.2)
t = 0.495 s
Note: x = voxt = 2 m
y = voyt + ½ayt2 = -1.2 m
2
1
2 1.2 m
y gt
  
2( 1.2)
9.8
t



R

34. Example 4 (Cont.): We now use horizontal
equation to find vox leaving the table top.
Use t = 0.495 s in x equation:
v = 4.04 m/s
1.2 m
2 m
R
Note: x = voxt = 2 m
y = ½gt2 = -1.2 m
2 m
ox
v t 
2 m
(0.495 s) = 2 m;
0.495 s
ox ox
v v 
The ball leaves the
table with a speed:

35. Example 4 (Cont.): What will be its speed
when it strikes the floor?
vy = 0 + (-9.8 m/s2)(0.495 s)
vy = vy + gt
0
vx = vox = 4.04 m/s
Note:
t = 0.495 s
vy = -4.85 m/s
2 2
(4.04 m/s) ( 4.85 m/s)
v   
4.85 m
tan
4.04 m
q


v4 = 146 ft/s q2 = 309.80
1.2 m
2 m vx
vy

36. Example 5. Find the “hang time” for the football
whose initial velocity is 25 m/s, 600.
vo =25 m/s
600
y = 0; a = -9.8 m/s2
Time of
flight t
vox = vo cos q
voy = vo sin q
Initial vo:
Vox = (25 m/s) cos 600; vox = 12.5 m/s
Voy = (25 m/s) sin 600; vox = 21.7 m/s
Only vertical parameters affect hang time.
2 2
1 1
2 2
; 0 (21.7) ( 9.8)
oy
y v t at t t
    

37. vo =25 m/s
600
y = 0; a = -9.8 m/s2
Time of
flight t
vox = vo cos q
voy = vo sin q
Initial vo:
2 2
1 1
2 2
; 0 (21.7) ( 9.8)
oy
y v t at t t
    
4.9 t2 = 21.7 t 4.9 t = 21.7
2
21.7 m/s
4.9 m/s
t  t = 4.42 s
Example 5 (Cont.) Find the “hang time” for the
football whose initial velocity is 25 m/s, 600.

38. Example 6. A running dog leaps with initial
velocity of 11 m/s at 300. What is the range?
v = 11 m/s
q =300
Draw figure and
find components:
vox = 9.53 m/s
voy = 5.50 m/s vox = 11 cos 300
voy = 11 sin 300
2 2
1 1
2 2
; 0 (5.50) ( 9.8)
oy
y v t at t t
    
To find range, first find t when y = 0; a = -9.8 m/s2
4.9 t2 = 5.50 t
2
5.50 m/s
4.9 m/s
t  t = 1.12 s
4.9 t = 5.50

39. Example 6 (Cont.) A dog leaps with initial
velocity of 11 m/s at 300. What is the range?
v = 10 m/s
q =310
Range is found
from x-component:
vx = vox = 9.53 m/s
x = vxt; t = 1.12 s vox = 10 cos 310
voy = 10 sin 310
Horizontal velocity is constant: vx = 9.53 m/s
Range: x = 10.7 m
x = (9.53 m/s)(1.12 s) = 10.7 m

40. Summary for Projectiles:
1. Determine x and y components v0
cos and sin
ox o oy o
v v v v
q q
 
2. The horizontal and vertical components of
displacement at any time t are given by:
2
1
2
ox oy
x v t y v t gt
  

41. Summary (Continued):
4. Vector displacement or velocity can then
be found from the components if desired:
3. The horizontal and vertical components of
velocity at any time t are given by:
;
x ox y oy
v v v v gt
  
2 2
R x y
  tan
y
x
q 