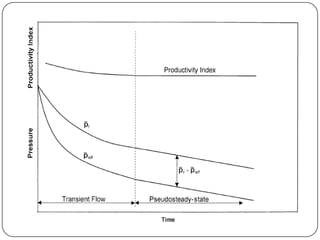
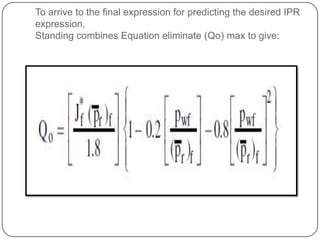
The document discusses various methods for measuring and predicting productivity and inflow performance relationships (IPRs) for oil wells. It defines productivity index J as the ratio of total liquid flow rate to pressure drawdown. Vogel's, Standing's, and Fetkovich's methods are empirical models for generating current and future IPRs. Vogel normalized IPRs using dimensionless parameters. Standing extended Vogel's method to predict future IPRs based on changes in reservoir pressure and productivity index over time. Fetkovich accounted for nonlinear well flow behavior in calculating theoretical productivity indices.

2. Productivity Index and IPR
 A commonly used measure of the ability of the
well to produce is the Productivity Index.
 Defined by the symbol ‘J’.
 The productivity index is the ratio of the total
liquid flow rate to the pressure drawdown.
 For a water-free oil production, the productivity
index is given by:

3.  where :
Qo = oil flow rate, STB/day
J = productivity index, STB/day/psi
pr = volumetric average drainage area pressure
(static pressure)
Pwf = bottom-hole flowing pressure
Dp = drawdown, psi

5.  The following empirical methods that are
designed to generate the current and future inflow
performance relationships:
 Vogel’s Method.
 Standing’s Method.
 Fetkovich’s Method.

6. Vogel’s Method.
 Vogel (1968) used a computer model to generate
IPRs for several hypothetical saturated-oil
reservoirs that are producing under a wide range
of conditions.
 Vogel normalized the calculated IPRs and
expressed the relationships in a dimensionless
form.
 He normalized the IPRs by introducing the
following dimensionless parameters:

8.  Vogel plotted the dimensionless IPR curves for all the
reservoir cases and arrived at the following
relationship between the above dimensionless
parameters:
 Where
Qo = oil rate at pwf
(Qo)max = maximum oil flow rate at zero wellbore
pressure,
pr = current average reservoir pressure, psig
pwf = wellbore pressure, psig

9. Standing’s Method
 Standing (1970) essentially extended the
application of Vogel’s to predict future inflow
performance relationship of a well as a function of
reservoir pressure.
 He noted that Vogel’s equation: Equation can be
rearranged as:

10. Standing introduced the productivity index J as defined by
Equation to yield:

11. Standing then defined the present (current) zero
drawdown productivity index as:

12. where J*p is Standing’s zero-drawdown productivity index.
The J*p is related to the productivity index J by:

13. To arrive to the final expression for predicting the desired IPR
expression,
Standing combines Equation eliminate (Qo) max to give:

14. where the subscript f refers to future condition.
Standing suggested that J*p can be estimated from the present value of J*p by the
following expression:

15. COMPUTATIONAL STEPS
 Standing’s methodology for predicting a future
IPR is summarized in the following steps:
 Step 1. Using the current time condition and the
available flow test data, calculate (Qo)max from
Equation 7-9 or Equation 7-18.
 Step 2. Calculate J* at the present condition, i.e.,
J*p, by using Equation. Notice that other
combinations of Equations 7-18 through can be
used to estimate J*p.

16.  Step 3. Using fluid property, saturation and
relative permeability data, calculate both
(kro/moBo)p and (kro/moBo)f.
 Step 4. Calculate J*f by using Equation. Use
Equation if the oil relative permeability data is not
available.
 Step 5. Generate the future IPR by applying
Equation.

17. Fetkovich’s Method
Muskat and Evinger (1942) attempted to account for the
observed nonlinear flow behavior (i.e., IPR) of wells by
calculating a theoretical productivity index from the
pseudo-steady-state flow equation. They expressed
Darcy’s equation as: