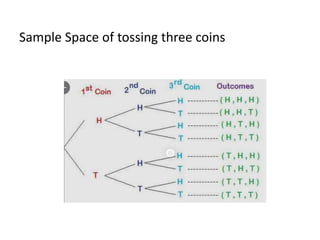
This document discusses probability theory and random processes. It defines key concepts such as random experiments, sample spaces, events, and probability. Random experiments are processes that can be repeated under the same conditions, with each repetition called a trial. A sample space contains all possible outcomes of an experiment. Events are subsets of outcomes from the sample space. Probability is defined axiomatically and through relative frequency. Examples are provided to demonstrate calculating probabilities of events using the classical definition. Properties of probability like mutually exclusive and conditional probability are also explained.

1. Probability Theory & Random Processes
Unit I Probability
Basic Concepts

2. Unpredictable & Random Phenomena
• Toss of coin
• Rolling a dice
• Number of A’s a student can obtain in a year
• Customer arriving at a business outlet
• Component failure in system
• Transaction requests arriving at a sever
• Messages received

3. Random Experiment
• If phenomenon or process can be repeated any number of
times under same conditions will be called experiment
each performance is called trial
• If each trial has more than one possible outcomes/results
then experiment is called random experiment
• The collection of all possible outcomes of an experiment is
called sample space denoted by S. The outcomes denoted
by wi , I = 1, 2, 3, …. n, are called sample points of sample
space.
• Event is the occurrence of one or any one of a number of
out comes.
• Event is a subset of sample space

4. Example 1
• If a die is tossed any one number from 1 to 6
appears. So the sample space of this
experiment is
S = {1, 2, 3, 4, 5, 6}
• The event “outcome is an even number” is a
subset of S and is
E = {2, 4, 6}

5. Sample Space of tossing three coins

6. Example 2
• Coin tossing experiment
• Outcomes are Head (H) and Tail (T)
• Space as result of three successive tosses is
S= {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
• The event “two heads and one tail” is
E= {HHT, HTH, THH}
• Event “at least one head” is
S= {HHH, HHT, HTH, HTT, THH, THT, TTH}

7. Example 3
• Rolling a dice twice or rolling two dice together
• Sample space
S = { (1,1), (1,2), (1,3), (1,4), (1,5), (1,6), (2,1), (2,2), (2,3), (2,4), (2,5), (2,6),
(3,1), (3,2), (3,3), (3,4), (3,5), (3,6), (4,1), (4,2), (4,3), (4,4), (4,5), (4,6),
(5,1), (5,2), (5,3), (5,4), (5,5), (5,6), (6,1), (6,2), (6,3), (6,4), (6,5), (6,6) }
• Event “sum of two numbers is 9”
E = {(3,6), (4,5), (5,4), (6,3)}























)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
6
6
5
6
4
6
3
6
2
6
1
6
6
5
5
5
4
5
3
5
2
5
1
5
6
4
5
4
4
4
3
4
2
4
1
4
6
3
5
3
4
3
3
3
2
3
1
3
6
2
5
2
4
2
3
2
2
2
1
2
6
1
5
1
4
1
3
1
2
1
1
1
S

8. Example 4
• Life span
– Sample space
S = {x | 0 ≤ x < ∞}
– Event : “Not more than 10 hours” is defined as
E= {x | 0 ≤ x < 10 (hours)}

9. Definitions of Probability
• Two approaches:
– Objective : based on experimental data
– Subjective: based on experience
• Defined in 3 ways:
– Axiomatic definition
– Relative Frequency Definition
– Classical Definition

10. Axiomatic Definition of Probability
• If a random experiment has a sample space
then for each event A of S the probability of
occurring of A is a number P(A) such that
following hold
– Axiom 1: 0 ≤ P(A) ≤ 1
– Axiom 2: P(S) = 1
– Axiom 3: For any set of n mutually exclusive events
A₁, A₂, A₃, ..... , An of the same sample space
P(A₁UA₂UA₃U ....UAn)= P(A₁)+P(A₂)+P(A₃)+ .... +P(An)

11. Relative Frequency Definition
• Consider a random experiment is performed n
times. If an event A occurs nA times, then
Relative Frequency = NA/N
n
n
A
P A
n 

 lim
)
(

12. Classical Definition
• The probability P(A) of event A is the ratio of
number of outcomes NA favourable to A to the
total number N of out comes in sample space
N
N
A
P A

)
(

13. Example
Two fair dice are tossed. Find the probability of each of following:
a) Sum of outcomes of two dice is 5
b) Sum of outcomes of two dice is 7 or 11
c) Outcome of second die is less than first die.
d) Outcomes of both dice are odd.
• Solution
Sample space
S = { (1,1), (1,2), (1,3), (1,4), (1,5), (1,6), (2,1), (2,2), (2,3), (2,4), (2,5), (2,6),
(3,1), (3,2), (3,3), (3,4), (3,5), (3,6), (4,1), (4,2), (4,3), (4,4), (4,5), (4,6),
(5,1), (5,2), (5,3), (5,4), (5,5), (5,6), (6,1), (6,2), (6,3), (6,4), (6,5), (6,6) }
N= 36
a) Event A "sum of outcomes of two dice is 5"
A = { (1,4), (2,3), (3,2), (4,1 } NA = 4 P(A) = 4/36 = 1/9
b) Event B "sum of outcomes of two dice is 7 or 11
B = { (1,6), (2,5), (3,4), (4,3), (5,2), (5,6), (6,1), (6,5) }
NB = 8 P(B)= 8/36 =2/9

14. c)Event C "Outcome of second die is less than first die"
C = { (2,1), (3,1), (3,2), (4,1), (4,2), (4,3), (5,1), (5,2), (5,3), (5,4), (6,1),
(6,2), (6,3), (6,4), (6,5)}
NC = 15 P(C) = 15/36 = 5/12
d) Event D "Outcomes of both dice are odd"
D = { (1,1), (1,3), (1,5), (3,1), (3,3), (3,5), (5,1), (5,3), (5,5) }
ND = 9 P(D) = 9/36 = ¼
This problem can also be solved by considering two dimensional
display of sample space.

15. Example: A die is rolled and a coin is tossed. What is
the probability that that die shows ODD number and
coin shows HEAD?
Sample space
S = {(1,H), (2,H), (3,H), (4,H), (5,H), (6,H),
(1,T), (2,T), (3,T), (4,T), (5,T), (6,T)} N = 12
Event
A = “die shows ODD number and coin shows HEAD”
= {(1,H), (2,H), (3,H), (4,H), (5,H)} NA = 3
N
N
A
P A

)
(
12
3

4
1


16. Applications of Probability
1. Reliability Engineering
2. Quality Control
3. Channel noise
4. System Simulation

17. SETS & Set Operations
• Set
• Null or Empty Set ɸ = {}
• Subset
• Number of subsets of set containing n elements 2ⁿ
• Union of sets AB
• Intersection of sets AB
• Complement set
• Difference sets A-B
• Mutually exclusive or Disjoint sets
• Complement of a set
• Venn Diagrams: Universal set, union, intersection,
difference and contained
B
A


18. Set Identities
• Commutative law of Union AB=BA
• Commutative Law of Intersection AB=B  A
• Associative Law of Union
(AB) C= A(B C)
• Associative law of Intersection
(A  B)  C= A (B  C)
• First Distribution Law
A (B  C)=(AB)  (AC)
• Second Distribution Law
A  (B C)=(AB)  (AC)
• De Morgan’s First Law
• De Morgan’s Second Law
B
A
B
A 


B
A
B
A 



19. More set identities
• For any subsets A and B of S the following hold
)
(
)
( B
A
B
A
A
S
A
A
A
A
S
A
S
S
A
B
A
B
A





















20. Properties of Probability
1. P(A) ≤ 1
2. Probability of complement of A is one minus
probability of A.
3. Probability of null event is zero.
4. If A is a subset of B, then P(A) ≤ P(B).
5. For any two events A and B
a) If events A and B are mutually exclusive then
P(AB)=P(A) + P(B)
b) P(AB)=P(A) + P(B) –P(AB)
c) P(A) = P(AB)+ P(AB)
6. Extension of 5 (b) to more than 2 events

21. Examples
• Two events A and B are mutually exclusive events with
P(A) = 0.4 and P(AB) = 0.7. What is P(B)?
• Consider two events A and B with known probabilities
P(A), P(B) and P(AB). Find the expression for the
event exactly one of the two events occurs in terms of
P(A), P(B) and P(AB).
• Two events A and B have the probabilities P(A)= 0.7,
P(B)= 0.4 and P(AB)= p. What is the range of p?
• Two events A and B have the probabilities P(A)= 0.5,
P(B)= 0.4 and P(AB)= 0.2. Compute the following
)
(
and
)
(
),
( B
A
P
B
A
P
B
A
P 



22. Conditional Probability
• If a die is tossed twice we get the sample space
• Let A denote the event “sum of two numbers is 9” and B the
event “first toss number is 5”.
• Conditional probability of event A given event B is denoted by
P(A|B) is given by























)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
6
6
5
6
4
6
3
6
2
6
1
6
6
5
5
5
4
5
3
5
2
5
1
5
6
4
5
4
4
4
3
4
2
4
1
4
6
3
5
3
4
3
3
3
2
3
1
3
6
2
5
2
4
2
3
2
2
2
1
2
6
1
5
1
4
1
3
1
2
1
1
1
S
)
(
)
(
)
|
(
B
P
B
A
P
B
A
P



23. Examples
1. A bag contains 8 red balls, 4 green balls and 8
yellow balls. A ball is drawn, it is not a red
ball. What is the probability that it is a green
ball?
2. A fair coin is tossed twice. Given that first
toss resulted in heads, what is the probability
that both tosses resulted in heads?

24. Partition of set
A partition of the set A is the set {A₁, A₂, A₃, .... , An}
with the following properties:
1.
This means A is set of subsets.
2.
This means that no two subsets have a common
element i.e subsets are mutually disjoint.
3.
Sub sets are collectively exhaustive that is
subsets together contain all elements of A
k
i
n
i
n
i
A
A k
i 



 ;
,.......
,
,
,
,.......
,
,
, 3
2
1
3
2
1

n
i
A
Ai ,.......
,
,
, 3
2
1


A
A
A
A
A n 




 ......
3
2
1

25. Total Probability
Let {A₁, A₂, A₃, .... , An} be a partition a sample space, and each of events A₁, A₂, A₃,
.... , An has a non-zero probability of occurrence. Let A be any event. Then
Proof: Event A can occur only if one of Aᵢ’s has occurred
Since {A₁, A₂, A₃, .... , An} is a partition of S,
{A  A₁, A  A₂, A  A₃, .... , A  An} is a partition of A
Because A occurs only if one of Aᵢ’s has occurred, therefore.
A = (A  A₁) (A  A₂)  (A  A₃)  ....  (A  An}
Since AAᵢ’s are mutually exclusive
P(A) = P(A  A₁) + P(A  A₂) + P(A  A₃) + .... + P(A  An}
Using the definition of conditional probability, we get the result







n
i
i
i
n
n
A
A
P
A
P
A
A
P
A
P
A
A
P
A
P
A
A
P
A
P
A
P
1
2
2
1
1
)
|
(
)
(
)
|
(
)
(
........
)
|
(
)
(
)
|
(
)
(
)
(

26. Example: A manufacturer produces cars in two factories. Ten percent cars produced in
factory A and 5% cars produced in factory B are defective. Factory A produces
100000 cars and factory B produces 50000 cars annually, compute the following:
(a) Probability of purchasing a defective car
(b) If the car is defective, probability that it was manufactured in factory A.
Solution:
Probability that car is defective and was produced in factory A
P(D|A)= 1/10
Probability that car is defective and was produced in factory B
P(D|B)= 1/20
Probability that car purchased was manufactured at factory A
P(A) = 2/3
Probability that car purchased was manufactured at factory B
P(B) =1/3
Probability that car purchased is defective
P(D) =P(D|A)P(A)+P(D|B)P(B)=
Probability that purchased car is defective was produced at factory A
P(A|D) =




3
1
20
1
3
2
10
1
12
1
)
(
)
(
)
|
(
D
P
A
P
A
D
P




12
1
3
2
10
1
5
4

27. Bayes’ Theorem
Let A and Bj be sets. Conditional probability requires that
where denotes intersection ("and"), and also that
Since
Therefore
If sets A form a partition of Sample space, that is
then
)
|
(
)
(
)
( A
B
P
A
P
B
A
P j
j 

)
|
(
)
(
)
( j
j
j B
A
P
B
P
A
B
P 

)
(
)
( j
j B
A
P
A
B
P 


)
(
)
|
(
)
(
)
|
(
A
P
B
A
P
B
P
A
B
P
j
j
j 
j
i
A
A
A
S j
i
i
n






,
,
1
1

i
n
i
n
A
A
A
A
S
A
A 








 1
1
1
1
)
(
 














n
i
i
n
A
A
P
A
A
P
A
P
1
1
1
1
)
(  



n
i
i A
A
P
A
P
1
1
|
)
(
 


 n
i
i
j
j
j
A
A
P
A
P
A
A
P
A
P
A
A
P
1
1
|
)
(
)
|
(
)
(
)
|
(

28. Example
• In a class 75% students are boys. On a particular
day 30% of boys and 25% of girls habitually wear
jeans. A student is selected randomly, what is the
probability that selected student is boy wearing
jeans?
• P(B)=
• P(G)=
• P(J|B)=
• P(J|G) =
• P(B|J)= )
|
(
)
(
)
|
(
)
(
)
|
(
)
(
G
J
P
G
P
B
J
P
B
P
B
J
P
B
P


29. Example:
While paying a bill a customer hands a note believing it to be of Rs100, the a
shopkeeper returns the change believing it to be note of Rs 50. An argument
arises. Both customer and shop keeper are honest but may make mistakes. If there
are 20 notes of Rs100 and 30 Notes of Rs 50; and shopkeeper identifies the notes
95% of the time, then what is the probability that customer’s claim is valid?
Solution
Event A = Customer gave Rs 50 Note
Event B = Customer gave Rs 100 Note
Event V = Customer’s claim is valid
Event L = shopkeeper says that it was Rs 50 note
The probability that customer’s claim is valid is the probability that customer gave
Rs 100 note given that shopkeeper said that it was Rs 50 note.
WE apply Bayes’ rule
6
0
30
20
30
.
)
( 


A
P 4
0
6
0
1 .
.
)
( 


B
P
)
|
(
)
(
)
|
(
)
(
)
( B
L
P
B
P
A
L
P
A
P
L
P 
 1
0
4
0
9
0
6
0 .
.
.
. 


 58
0.

)
(
)
(
)
|
(
)
|
(
L
P
V
P
V
L
P
L
V
P 
58
0
4
0
1
0
.
.
. 


30. Application in transmission channels
• Discrete channel
An input alphabet X={x₁, x₂, x₃, ..... , xn }, an output alphabet
Y={y₁, y₂, y₃, ..... , ym } and set of conditional probabilities
of receiving symbol when symbol is transmitted i.e
• The probabilities are known as Transmission Probabilities.
• Binary Channel: m = n = 2
• Symmetric channel:
• Probability of error: In a binary channel an error occurs if
y₂ is received when x₁ is transmitted or if y₁ is received
when x₂ is transmitted. Therefore
• Pe = P(x₁)P(y₂|x₁)+P(x₂)P(y₁|x₂)
ij
P
j
y i
x
m
j
n
i
x
y
P
P i
j
ij ,.......,
3
,
2
,
1
;
.,
,.........
3
,
2
,
1
);
|
( 


ji
ij P
P 

31. Example: Consider the binary symmetric channel shown in the figure. If the
probability of transmitting x is 0.6, and probability of receiving a when x is
transmitted and of receiving b when y is transmitted 0.9; compute the following
1. Probability that x was transmitted given that b was received
2. Probability that y was transmitted given that a was received
3. Probability that x was transmitted given that a was received
4. Probability that y was transmitted given that b was received
5. Probability error
Solution
We have P(x) =0.6, P(a|x) = 0.9, P(b|y) = 0.9
P(y) = 0.4, P(a|y) = 0.1, P(b|x) = 0.1
P(a) = P(a|x)P(x)+P(a|y)P(y) = 0.9×0.6+0.1×0.4=0.58
P(b) = P(b|x)P(x)+P(b|y)P(y) =0.1×0.6+0.9×0.4 =0.42
Apply Bayes’ rule to compute
x
y b
a
9
.
0
)
|
(
11 
 x
a
P
P
9
.
0
)
|
(
22 
 y
b
P
P
1
.
0
)
|
(
21 
 y
a
P
P
1
.
0
)
|
(
12 
 x
b
P
P
)
(
)
(
)
|
(
)
|
(
b
P
x
P
x
b
P
b
x
P 
)
(
)
(
)
|
(
)
|
(
a
P
y
P
y
a
P
a
y
P 
)
(
)
(
)
|
(
)
|
(
a
P
x
P
x
a
P
a
x
P 
)
(
)
(
)
|
(
)
|
(
b
P
y
P
y
b
P
b
y
P 
)
|
(
)
(
)
|
(
)
( y
a
P
y
P
x
b
P
x
P
Pe 

143
.
0
7
1

 069
.
0
29
2


931
.
0
29
27

 857
.
0
7
6


1
.
0


32. Independent events
Two events A and B are independent if occurrence one after the other, does not
dependent on the occurrence of first. i.e
P(A|B) =P(A) and P(B|A) = P(B)
Since by definition of conditional probability
P(A|B)P(B) = P(A ∩ B) =P(B|A)P(A)
We conclude
Two events A and B are independent iff P(A ∩ B) = P(A)P(B)
This result can be extended to any number of events:
If A₁, A₂, A₃, ....... , An are n independent events, then
P(A₁ ∩ A₂ ∩ A₃ ∩ ....... ∩ An ) = P(A₁) P(A₂) P(A₃) ....... P(An )

33. • If A and B are independent events show that and B; A and ; and are also
independent events
Proof :
The events and are mutually exclusive and , therefore
A B A B
B
A  B
A      B
B
A
B
A 



    P(B)
B
A
P
B
A
P 



   
B
A
P
-
P(B)
B
A
P 


   
A)P(B
P
-
P(B)
B
A
P 

  P(A)]
-
P(B)[1
B
A
P 

t.)
independen
are
B
and
A
(
  )
A
P(B)P(
B
A
P 
 t.
independen
are
B
and
A

     
B
A
P
B
A
P
B
A
P 




 1     B)
P(A
P(B
A)
P
B
A
P 




 1
    P(A)P(B)
P(B
A)
P
B
A
P 



 1 t.)
independen
are
B
and
A
(
    P(A)]
P(B
A)]
P
[
B
A
P 



 1
[
1
    )
B
)P(
A
P(
]
P(B
A)][1
P
[
B
A
P 



 1 t.
independen
are
B
and
A


34. Example
A red and a white die are tossed together . Find the probability that red die gives
number 4 and white die gives number 3.
Solution:
Event A : Red die gives number 4
Event B : White die gives number 3
Event C : Red die gives number 4 and White die gives number 3
C = A∩B
6
1
P(A) 
6
1
P(B) 
36
1
B)
P(A
P(C) 


P(B)
P(A)
B)
P(A
that
Note 


35. Permutations nPr or P(n, r)
In permutations order is important
Example 1: How many words can be formed by using letters in SAMPLE?
Answer:
The words may have 1 ,2, 3, 4, 5 or 6 letters. All will be distinct .
Number of words that can be formed is
N = P(6, 1) + P(6, 2) + P(6, 3) + P(6, 4) + P(6, 5) + P(6, 6)
=6 +30 +120 +360 +720 +720 = 1956
Example 2: How many words can be formed by using all the letters in STATISTICS ?
Answer:
There are 10 letters in the word STATISTICS, 1 A, 1 C, 2 I’s, 3 T’s and 3 S’s.
Number of words formed in this case is
!
!
!
!
N
3
3
2
10


 N 50400


36. Example:
Ten books are placed in a row randomly. Find the probability that 3 books are
always together .
Solution:
Number of ways of arranging 10 books = 10!
We consider 3 books as 1 book and arrange 8 books.
Number of ways of arranging 8 books = 8!
Number of ways of arranging 3 books = 3!
Therefore,
Number of ways of arranging 10 books so that 3 books are always together = 8! 3!
books
10
arranging
of
ways
of
Number
together
placed
are
books
3
that
such
books
10
arranging
of
ways
of
Number
P 
10!
3!
8!
P 
9
10
2
3



5
1


37. Combinations nCr or C(n, r) or
Example : There are m boys and n girls in a class. A team of k students is to be
selected.
(a) How many teams can be formed?
Answer: C(n+m, k)
(b) How many teams can be formed if there are i boys in each team?
Answer: C(n, i) C(m, k-i)
If we consider all teams as defined in (b) with i = 0, 1, 2, ......, k; then
If n = m = k
)
(n
r
!
)!
(
!
)
,
(
r
r
n
n
r
n
C

 )
,
( r
n
n
C 






k
i
i
k
m
C
i
n
C
k
m
n
C
1
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
.
..........
)
,
(
)
,
(
......
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
0
2
2
1
1
0
2
n
C
n
n
C
i
n
n
C
i
n
C
n
n
C
n
C
n
n
C
n
C
n
n
C
n
C
n
n
C










2
2
2
2
2
2
1
0
2 )]
,
(
[
.
..........
)]
,
(
[
......
]
)
,
(
[
)]
,
(
[
)]
,
(
[
)
,
( n
n
C
i
n
C
n
C
n
C
n
C
n
n
C 







38. Example
From a box containing 3 red and 2 black balls 2 balls are drawn at random. Find the
probability that both balls are (a) red (b) of same colour
Solution:
2
5
2
3
C
C
red)
balls
P(Both 
Black)
or
Red
are
balls
P(Both
color)
same
balls
P(Both 
Black)
are
P(Both
)
Red
are
P(Both 

2
5
2
2
2
5
2
3
C
C
C
C


10
3

5
2


39. Example: A committee of seven persons is to be formed out of a pool of 10 men and
12 women.
1. What is the probability that committee will contain 3 men and 4 women.
2. What is the probability that committee will contain all women.
Solution:
The number of committees that can be formed
A = committee of 3 men and 4 women
NA = Number of committees of 3 men and 4 women = C( 10, 3) C( 12, 4) = 59400
P(A) = NA/N = 0.35
B = Committee containing all women
NB = Number of committees containing all women = C(12, 7) = 792
P(B) = NB/N = 0.005
)
,
( 7
12
10
C
N
)!
(
!
!
7
22
7
22

 170544
